臺風強度模擬的海溫目標觀測研究

姚佳偉 段晚鎖

1 中國科學院大氣物理研究所大氣科學和地球流體力學數值模擬國家重點實驗室，北京 100029

2 中國科學院大學地球與行星科學學院，北京 100049

1 引言

熱帶氣旋（Tropical Cyclone; TC）是破壞性最大的天氣系統之一，常常給沿海國家和地區的人民生命財產安全造成巨大損失（Peduzzi et al., 2012），因此，TC 的預報具有重要意義。隨著衛星、雷達等觀測資料的完善、資料同化技術的改進以及數值模式質量的提高，TC 路徑預報技巧顯著提高（Rogers et al., 2006）。對于TC 強度，因為其受到不同尺度因子相互作用的影響（Montgomery and Smith, 2017），機理相對更復雜，從而導致TC 強度的預報具有很大挑戰性。

已有研究表明，TC 強度預報的不確定性受到多種誤差來源的影響。Emanuel and Zhang（2016）研究指出，在TC 發展的初始階段，初始渦旋誤差對TC 強度預報誤差起主要作用；而在隨后階段，路徑及垂直風切變誤差對TC 強度預報誤差影響較大。Nasrollahi et al.（2012）研究表明，參數化過程（如積云對流參數化）的不確定性對TC 強度預報模擬也有重要的影響（亦見Parker et al., 2017）。事實上，前人的工作主要考慮了大氣的初始場不確定性或參數不確定性對TC 強度預報誤差的影響，而很少考慮海溫誤差的影響，甚至認為海表溫度（SST）對TC 強度影響較小（Evans, 1993；Parker et al., 2017）。然而，大量的觀測和理論研究表明，TC 和海洋之間存在強烈的相互作用。如Emanuel（1988）提出的MPI（Maximum Potential Intensity）理論將TC 看作一個熱機，TC 最大的可能強度（MPI）取決于下墊面的SST 與對流層出流溫度，而Demaria and Kaplan（1994）以及Schade（2000）研究表明，當海溫大于24°C 時，對流層出流溫度與SST 存在線性關系。綜合兩者可知，TC 的MPI是由SST 所決定的。Emanuel et al.（1994）提出WISHE（Wind Induced Surface Heat Exchange）機制，進一步表明了SST 對TC 強度發展具有重要影響。另外，由于TC 對海洋的抽吸和攪拌作用，伴隨著SST 的冷卻現象（Price, 1981; Shay et al.,1992; Schade and Emanuel, 1999; Srinivas et al.,2016），臺風內部向上的熱通量會被抑制，進而抑制TC 強度增強，從而使得實際觀測或者模擬的TC 強度低于MPI 理論的結果。特別地，Torn（2016）研究指出，SST 不確定性對TC 強度預報的影響大于模式參數不確定性的影響，尤其在預報或模擬的后期階段，SST 不確定性對強度預報的影響與大氣不確定性的影響是相當的。

目前大部分TC 業務預報模式采用固定的海溫條件，這樣就忽略了SST 負反饋過程的作用（Winterbottom et al., 2012; Sun et al., 2014）；即使采用耦合模式，由于模式本身的不確定性，或者耦合頻率較低等問題，耦合模式模擬的SST 也會存在誤差（Davis et al., 2008; Scoccimarro et al., 2017）。所以，SST 誤差在TC 預報或模擬中是不可避免的。從以上討論可以看出，這里的SST 誤差不僅可以理解為由于海溫觀測的不準確或者耦合模式TC 與海洋相互作用描述不夠完美而導致的。

基于上述討論，我們自然會問：如何提高SST 強迫場的準確性或者與TC 強度相關的TC—海洋相互作用的模擬水平，進而提高臺風強度的預報水平？毫無疑問，增加觀測是提高SST 強迫場準確性的有效途徑。同時，為了在耦合模式中準確刻畫TC—海洋的相互作用，模式研究者也是基于大量的觀測事實去構建能夠反映TC—海洋相互作用的優化模型，從而改進海溫的模擬能力。顯然，兩個方面都需要增加觀測來實現。那么，為了有效提高TC 強度的模擬水平，我們究竟應該在哪個區域或者臺風演變的哪個階段對SST 優先進行觀測呢？該問題實際上涉及到始于1990s 的“目標觀測”新策略（Snyder, 1996; Mu, 2013）。目標觀測是作為改善初始場問題被首先提出的，主要思路如下：為了提高某一天氣、氣候事件在未來時刻（驗證時刻）在所關心的區域（驗證區域）的預報技巧，而在此時刻之前的某一時刻（目標時刻），在一些關鍵區域（亦稱“敏感區”）增加額外觀測，通過同化這些額外觀測而形成一個更加合適的初始場，從而最大限度地減小驗證區域的預報誤差（詳見Mu,2013）。

如上所述，目標觀測被用于減小初始誤差（Petersen and Thorpe, 2007; Wu et al., 2007; Buizza et al., 2007; Qin and Mu, 2012; Duan and Hu, 2016）。為了探究外強迫的不確定性對模擬技巧的影響，Wen and Duan （2019）將目標觀測的思想拓展到減小外強迫誤差，分析了究竟哪個區域的觀測能夠有效地減小強迫誤差的影響，而提高數值模式模擬技巧。在本研究中，我們擬從SST 強迫對TC 強度模擬的影響的角度探討TC 強度模擬的不確定性。所以，我們采用Wen and Duan（2019）提出的外強迫目標觀測思路，即探討對TC 強度模擬影響最大的SST 強迫目標觀測。

目標觀測的關鍵是確定目標觀測敏感區。根據Wen and Duan（2019）的思路，若要確定外強迫目標觀測敏感區，應首先確定對TC 強度模擬不確定性影響最大的SST 外強迫誤差。事實上，Yao et al.（2021）已經利用WRF 模式探討了SST 強迫不確定性對西北太平洋12 個TC 強度模擬的影響，并獲得了對TC 強度影響最大的海溫強迫誤差模態，即具有非線性強迫奇異向量（NFSV）空間結構的SST 強迫誤差。NFSV 是指能夠導致最大預報誤差或模擬誤差的外強迫誤差（Duan and Zhou, 2013）。該方法已被成功應用于臺風、厄爾尼諾和源區黑潮等高影響天氣氣候事件的可預報性研究中（Duan and Zhao, 2015; Wen and Duan, 2019; Qin et al.,2020），獲得了有意義的結果。不同于初始場的目標觀測，強迫場的目標觀測策略既涉及到在哪個區域進行目標觀測，又需要考慮在哪個時段進行目標觀測能取得最優的效果。如上所述，Yao et al.（2021）已經得到了對TC 強度模擬不確定性影響最大的NFSV 型SST 強迫誤差。NFSV 型SST 強迫誤差是定常的，它可以理解為對臺風強度模擬具有最大影響的SST 強迫的系統性偏差，也可理解為模擬時段內對TC 強度影響最大的SST 強迫誤差的均值。另外，定常的NFSV 型SST 強迫誤差，使得TC 強度模擬在每個時刻受到相同大小和相同空間分布的海溫強迫誤差的影響，這便于我們在相同條件下比較TC 強度模擬不確定性對不同時段SST 強迫誤差的敏感依賴性，從而獲得SST 強迫的最優目標觀測時段。因此，在上述研究的基礎上，本文針對臺風強度模擬的海溫目標觀測，提出以下問題：（1）如何根據NFSV 型SST 強迫誤差確定TC 強度模擬在海洋上的SST 目標觀測布局以及最優觀測時段？（2）最優觀測時段的目標觀測及其觀測布局能在多大程度上改進TC 強度的模擬水平？

2 WRF 模式及方法

本文使用WRF-ARW（The Weather Research and Forecasting Model，the Advanced Research WRF）3.8.1 版本。WRF 模式是中尺度非靜力可壓縮的大氣動力模式，常常用于TC 強度和路徑的預報研究。對于WRF 模式，本文采用如下參數化過程：（1）云微物理過程，采用Lin et al.（1983）提出的參數化方案；（2）積云對流過程，采用Kain-Fritsch 方案（Kain, 2004）；（3）長、短波輻射參數化過程，分別采用Rapid Radiative Transfer Model（RRTM;Mlawer et al., 1997）和Dudhia 參數化方案（Dudhia,1989）；（4）邊界層參數化過程，采用Yonsei University 的參數化方案（Hong et al., 2006）。為了考慮海洋對TC 強度模擬的影響，該研究引入了隨時間變化的海溫強迫場，即通過每6 小時輸入觀測的SST 來強迫WRF 模式；在差分網格分辨率上，水平網格采用30 km×30 km，設置垂直方向24 層，而頂層為50 hPa；模式的時間積分步長為90 s，每個臺風模擬積分時長為5 天，每3 小時輸出一次結果，共40 個輸出時次。模式初始化中用到的大氣資料（包括風、溫、壓、濕、降水等）來自于美國國家大氣環境研究中心（the National Centers for Environmental Prediction，NCEP）的FNL 再分析數據，其精度為1°×1°；地形高度也是采用NCEP提供的高精度地形數據；觀測的海溫資料來自于NCEP 的實時海溫再分析，精度為0.083°×0.083°。因為NCEP 的海溫再分析是逐日資料，不符合模式積分步長的時間，所以本研究將逐日的海溫資料進行了時間上的插值，得到了步長為6 小時的海溫強迫場，然后用于WRF 模式強迫大氣。

該研究仍然采用Yao et al.（2021）所研究的12 個TC 個例。這些TC 個例的移動路徑受SST 強迫誤差的影響很小，從而排除了移動路徑的變化對TC 強度的影響。基于Yao et al.（2021）揭示的NFSV 型SST 強迫誤差，本文采用觀測系統模擬試驗（OSSE）確定TC 強度模擬的SST 目標觀測布局及最優觀測時段。所謂OSSE，即首先將在模式合理設置下的一次數值模擬作為“真實”場（Nature Run），并基于該“真實”場的格點構建模擬觀測資料，然后評估加入模擬觀測資料后的預報與“真實”場的擬合程度，以此分析觀測系統的觀測對數值模擬效果改善的程度（Privé et al.,2021）。該方法不考慮模式誤差的影響，它使用模擬觀測，將其同化到模式初始場，避免了因為缺少觀測而無法提供模式初始場進行模擬研究的局限性，該方法可為未來的觀測提供合理有效的建議（Arnold and Dey, 1986）。具體到該研究考慮的SST 外強迫場，采用的OSSE 步驟如下：（1）對所研究的TC，將其演變過程中每6 小時所對應的再分析SST 場作為“真實”的隨時間變化的SST，應用于WRF 的強迫場；采用FNL 初始分析場作為大氣初始場，積分WRF 120 小時，作為“Nature Run”。（2）根據Yao et al.（2021）研究中的198 個海溫強迫擾動試驗結果，遴選出對TC 強度有較大影響的20 個SST 強迫誤差（以SST 強迫誤差引起的TC 強度在整個模擬區間的總誤差超過300 hPa來衡量），將其疊加到“真實”的SST 強迫場，并l 積分模式120 小時，作為“Control Run”。（3）根據NFSV 型SST 強迫誤差確定目標觀測布局的網格點。（4）在模擬過程中的各個時刻的觀測網格點上構造模擬觀測，并將其同化到“Control Run”的SST 強迫場，得到更新的SST 強迫分析場。（5）用更新的SST 強迫分析場替換步驟（1）中“真實”的SST 強迫場，積分模式120 小時，將得到的模擬結果記為“Sensitive Run”，并與“Control Run”比較，考察目標觀測在提高臺風強度模擬技巧中的有效性。根據試驗目的的差異，該研究將OSSEs 分為兩類，OSSE-S 和OSSE-T。在OSSE-S 中將進行4 組OSSEs，每組試驗的區別在于第三步驟不同，詳見表1；在OSSE-T 中將進行2 組OSSEs，每組試驗區別在于第五步驟不同，詳見表2。

表1 OSSE-S 第三步設置說明Table 1 Settings of Step 3 of OSSE-S

表2 OSSE-T 第五步設置說明Table 2 Settings of Step 5 of OSSE-T

為評估目標觀測對TC 強度模擬的改善程度（ η），采用公式（1）作為度量：

其中，ECtrl為“Control Run”相對于“Nature Run”的TC 強度誤差，ESen為“Sensitive Run”相對于“Nature Run”的TC 強度誤差。TC 強度誤差E采用公式（2）計算：

其中，Pn為“Nature Run”的TC 強度，P為“Sensitive Run”或“Control Run”的TC 強度，這里的TC 強度采用最小海平面氣壓度量。

該研究采用最優差值（Optimal Interpolation，OI）資料同化方法同化SST 模擬觀測。最優插值方法的同化公式如下：

其中，Xa是分析場，Xb為背景場，y是觀測值；H為從背景場到觀測場的映射矩陣，即觀測算子；K為增益矩陣，如公式（4）所示：

這里的B為背景誤差協方差矩陣，O為觀測誤差協方差矩陣；下面的公式（5）給出的是權重系數wi,j（即第j個模式格點到第i個觀測點的權重系數）的計算公式，采用了距離平方反比：

3 最優目標觀測布局和最優觀測時間的確定

對于強迫場的目標觀測，其關鍵既要確定目標觀測敏感區，又要識別最優的目標觀測時段。根據Yao et al.（2021）的結論，NFSV 型SST 強迫誤差對TC 強度模擬不確定性具有最大影響，且NFSV 誤差的大值區主要位于TC 的移動路徑上，發生在TC 快速增強階段（如圖1 所示）。該結論意味著，NFSV 型SST 強迫誤差導致TC 強度最大的模擬誤差，代表了TC 強度模擬的最敏感的SST誤差，而誤差的大值區則表明了TC 強度模擬對該區域以及對應時段的SST 誤差最敏感。如果在該區域和相應時段增加額外觀測，改善SST 強迫場，則TC 強度的模擬水平可能會明顯改善。所以，NFSV 型SST 強迫誤差的大值區可能代表了TC 強度模擬的海溫目標觀測敏感區，其所在階段也可能代表了TC 強度模擬對海溫目標觀測的敏感階段。因此，我們可以根據NFSV 型SST 強迫誤差的大值區來確定TC 強度模擬的SST 目標觀測布局以及最優觀測時段。

3.1 最優目標觀測布局的確定

理論上，在NFSV 型SST 強迫誤差場中，網格點上誤差越大意味著TC 強度模擬對該格點誤差越敏感，而目標觀測就越應該布置在該格點的位置。為了確定能夠有效提高TC 強度模擬水平的目標觀測的最優觀測布局，我們首先進行兩組OSSE 試驗，即OSSE-S-I 和OSSE-S-II，并以圖1 中TC 個例Soulik 為例進行介紹。

圖1 12 個TC 個例的非線性強迫奇異向量（NFSV）型SST 強迫誤差結構（陰影，單位：K）。其中點為TC 的路徑；藍色、綠色、黃色、紅色、紫色的點分別代表模擬TC 強度大小在980～1000 hPa、970～980 hPa、960～970 hPa、950～960 hPa 和900～950 hPa 的范圍內Fig. 1 Patterns of Nonlinear Forcing Singular Vector (NFSV)-type SST forcing errors (shaded, units: K) of the selected 12 TC cases. The dots represent the tracks of TCs and the blue, green, yellow, red, and purple dots indicate the simulated TC intensity within 980-1000 hPa, 970-980 hPa,960-970 hPa, 950-960 hPa and 900-950 hPa

OSSE 試驗的步驟如第二節所示，OSSE-S-I和OSSE -S-II 的差別在于第三步，即目標觀測的布局不同。OSSE-S-I 的第三步是根據NFSV 型SST 強迫誤差大小，依次在誤差大小排名前20、40、60、···、120、140、···、240 的格點分別構建模擬觀測。當構建的觀測數低于120（即選取的格點數低于120）時，目標觀測敏感區主要分布于（20°N～26°N，132°E～140°E）（記為區域A）；當選取的格點數超過120 時，在（24°N，130°E）附近出現新的目標觀測區（如圖2 所示）。

圖2 Soulik 個例的NFSV 型SST 強迫誤差中前20、40、···、240 個大值點所構成的敏感區范圍Fig. 2 Regions of the sensitive area identified by the leading 20, 40, ···, 240 large values of the NFSV-type SST forcing error for TC Soulik

這里的模擬觀測是在“真實”的SST 上疊加服從N（0，0.1）分布的隨機誤差而構造的。選取上述不同數目的模擬觀測，將其同化到“Control Run”的SST 強迫場，利用更新的SST 強迫場積分WRF，考察TC 強度模擬誤差的變化情況。結果表明，如果僅同化NFSV 型SST 強迫誤差前20個大值點的模擬觀測時，即可使得TC 強度模擬誤差減小67%（如圖3 所示），而且隨著同化模擬觀測數的進一步增加，TC 強度模擬技巧的改善程度逐漸增加，并在同化的模擬觀測數達到120 時，TC 強度模擬改善程度達到峰值，模擬誤差減小達到76.8%。然而，當目標觀測敏感區范圍進一步擴大，同化的模擬觀測數進一步增加時，TC 強度模擬的改善程度會出現一定程度的下降（見圖3）。

圖4 給出了同化不同數量模擬觀測后，SST 強迫場的改善情況。從圖中可以看出，當模擬觀測數少于120 時，SST 強迫誤差主要減小的是區域A的誤差，且SST 誤差減小幅度隨著模擬觀測數的增加而增大（如圖5 所示）；而當模擬觀測數超過120 以后，SST 強迫誤差減小的主要區域轉移到區域B（即20°N～26°N，128°E～132°E ；圖4），且區域A 的SST 誤差的改善程度傾向于隨著觀測數的增加達到飽和后降低（圖5）。這種SST 強迫誤差改善程度的變化規律恰恰對應了上述隨著同化的模擬觀測數的增加，TC 強度模擬改善程度達到飽和，然后轉而減小的變化規律。另外，我們注意到區域A 與NFSV 型SST 強迫誤差的大值區有較多重合，而區域B 并未位于NFSV 型SST 強迫誤差的大值區（圖4）。綜合這些結果，我們可以推斷，區域A，即NFSV 型SST 強迫誤差值更大的區域，代表了TC 強度模擬的目標觀測敏感區，該區域SST 強迫誤差的減小能有效改善TC 強度的模擬水平，所以SST 強迫的目標觀測應優先布放在NFSV 型SST 強迫誤差的前120 個格點，即區域A。

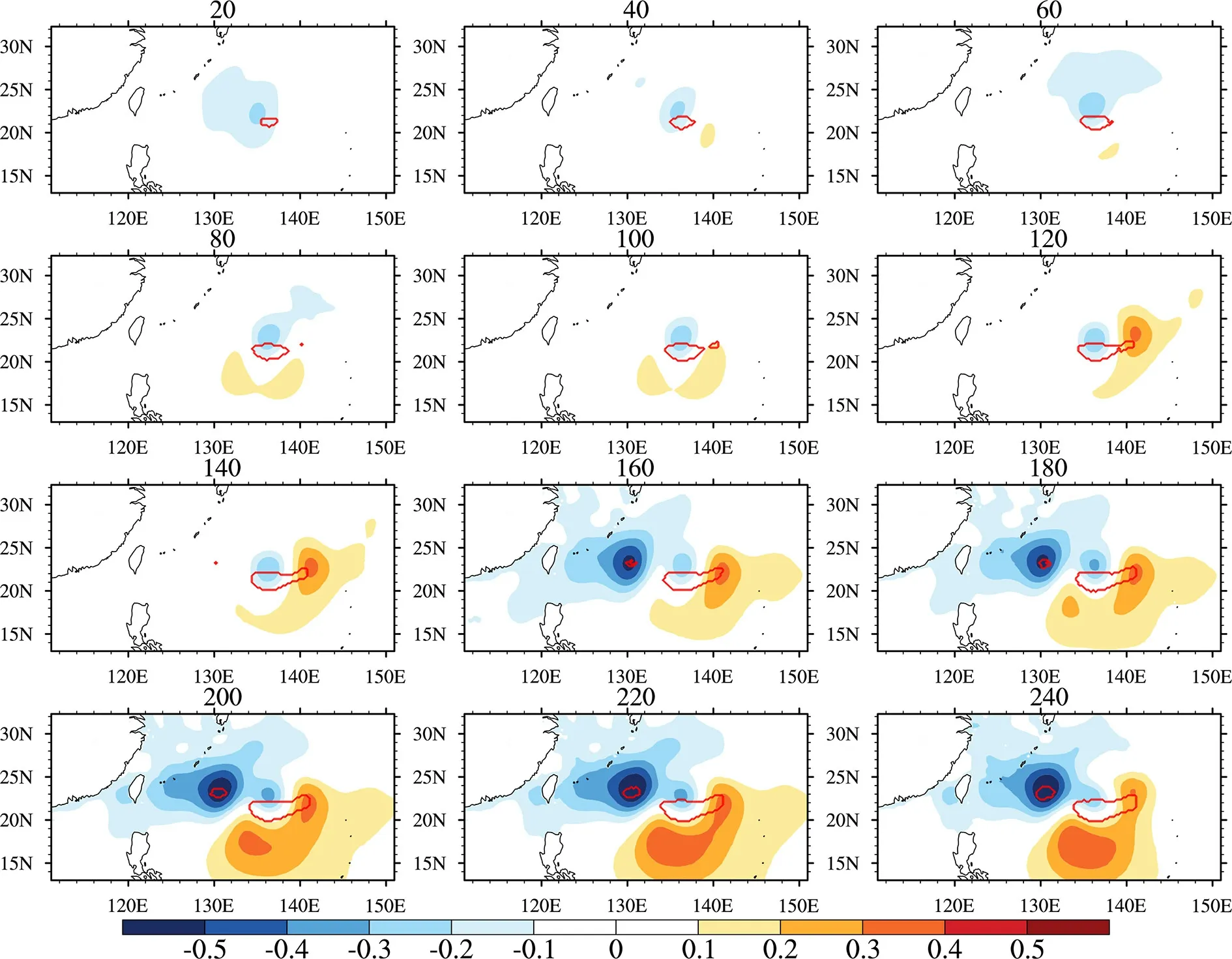
圖4 同化敏感區范圍內的觀測后，SST 強迫場的變化情況（填色，單位：K）。其中紅色實線框出的范圍表示對應的目標觀測敏感區Fig. 4 Change of SST (shaded, units: K) forcing field after assimilating the observations in the sensitive area to different extents. The red line represents the extent of the corresponding sensitive area of the target observations

在OSSE-S-I 試驗中，我們對敏感區內的每個格點都構建了模擬觀測，但從圖5 的結果可以發現，當構建的模擬觀測數從20 增加至120 的過程中，同化增加的模擬觀測使得區域A 減小的SST 誤差從1.3 K 增加到1.5 K。由此可以看出，在模擬觀測數20 的基礎上，進一步增加的模擬觀測使得SST 誤差減小的收益是減小的。那么，這種事實是否意味著，我們并不需要對敏感區內所有的格點進行觀測，便可以在TC 強度模擬技巧的改善中獲得與所有格點進行觀測相當的效果呢？為回答該問題，本文設計了OSSE-S-II 試驗。OSSE-S-II 的各個試驗步驟與OSSE-S-I 基本相同，只在第三步驟略有不同，不同之處在于OSSE-S-II 在該步驟獲得的目標觀測布局是在OSSE-S-I 的目標觀測布局基礎上，分別選取不同間隔（即30 km、60 km、90 km、120 km）的觀測進行同化。不同間隔對應了敏感區內不同的觀測數（如表3 所示）。

表3 OSSE-II 中敏感區內不同觀測布局的觀測數Table 3 Numbers of observations with different intervals in the sensitive area of OSSE-II

圖5 OSSE-S-I 中，同化不同范圍敏感區內的模擬觀測后，區域A 所減小的絕對SST 誤差大小（單位：K）Fig. 5 Absolute reduced SST errors in region A after assimilating the observations in sensitive areas to a different extent in OSSE-S-I (units: K)

圖6 給出的是不同觀測間隔下，同化敏感區內SST 模擬觀測對TC 強度模擬的改善情況。從圖中可以看出，在敏感區內所有格點上進行觀測，對TC 強度模擬改善程度最高，但當觀測數達到120 時，每個觀測的平均收益是很低的。但當我們以90 km 為間隔構建模擬觀測時，只需要12 個觀測點，便能夠使TC 強度模擬的改善效果達到75%，這僅僅略低于在敏感區所有格點進行觀測后的改善效果76.8%，但觀測數卻減少了90%。雖然進一步增大觀測間隔至120 km，觀測數僅有7 個，而且每個觀測對TC 強度模擬改善的平均收益是最高的，但是對TC 強度的模擬改進程度卻降低至73%。所以，如果綜合考慮TC 強度模擬的改善效果及觀測的成本，選取90 km 作為觀測間隔在敏感區內構建觀測網可能是更優策略。

圖6 OSSE-S-II 的模擬結果。同化目標觀測敏感區不同觀測間隔的觀測后，TC 強度模擬的改善程度Fig. 6 Results of OSSE-S-II. The improvement rate in the TC intensity simulation after assimilating observations with different intervals in the sensitive area

3.2 最優觀測時段的確定

在實際業務預報中，海溫強迫是持續作用在模式場上，這意味著在各個時刻都存在海溫強迫誤差對TC 強度的負面影響。然而，根據Yao et al.（2021）的結果，TC 強度對海溫強度誤差存在時間上的敏感依賴性，并且NFSV 型SST 強迫誤差的大值區對應了TC 強度對海溫誤差最敏感的階段。因此，我們根據NFSV 型SST 強迫誤差確定目標觀測的最優時間段。為此，基于OSSE-S-I 和OSSE-S-II 的結果，我們設計了OSSE-T-I 試驗，并以Soulik 個例進行說明。

OSSE-T-I 的步驟亦如第二節所述，但其第三步采用OSSE-S 試驗中所確定的最優觀測布局，第五步只在第0 h，6 h，12 h，···，114 h 替換步驟（1）中對應時刻“真實”的SST 強迫場，并積分模式120 小時。由此，我們可以根據同化后對TC強度模擬改善程度的差異確定出最優觀測時段。試驗結果如圖7 所示。結果表明，盡管僅在單個時刻進行目標觀測改善SST 強迫場，對TC 強度模擬的改善效果不大，但是從圖中可以明顯看出，在18～54 h 這個階段進行目標觀測對TC 強度的模擬具有更為明顯的改善。對比NFSV 型SST 強迫誤差的結構，我們很容易發現，這個階段恰好對應于NFSV 型SST 強迫誤差的大值區所對應的TC 時段，一般處于臺風快速增強階段。由此，當我們進行目標觀測時，我們可以根據NFSV 型SST 強迫誤差大值區所對應的TC 快速增強階段確定最優觀測時間。

圖7 OSSE-T-I 的模擬結果。在單個時刻同化敏感區內的模擬觀測對TC 強度模擬的改善情況。虛線為改善程度達5%的參考線Fig. 7 Result of OSSE-T-I. The improvement rate of the simulation of the TC intensity after assimilating observations in the sensitive region only once at the corresponding time. The dashed line is the reference line of the 5% improvement

對于圖1 中的其他個例，試驗結果也都表明，當模擬的觀測數選取在NFSV 型SST 強迫誤差的前120 個格點，且以90 km 間隔布放觀測時，同化這些觀測會對TC 強度的模擬有更好的改善且最大程度節省觀測成本；同時，NFSV 型SST 強迫誤差大值區所對應的TC 階段亦與最優目標觀測時段一致，這里不再贅述。綜上所述，根據NFSV 型SST 強迫誤差結構，通過OSSE-S-I 及OSSE-S-II確定了TC 強度模擬的SST 目標觀測敏感區以及敏感區內的觀測布局，即選取NFSV 型SST 強迫誤差中前120 個誤差大值點作為目標觀測敏感區，并在敏感區中以90 km 為間隔布置觀測；通過OSSET-I 確定了TC 強度模擬的SST 目標觀測的優先觀測時段，即NFSV 型SST 強迫誤差的大值區對應臺風快速增強階段。

4 目標觀測的有效性

上節討論了在NFSV 型SST 強迫敏感區內如何以及何時布放觀測能夠最大程度提高TC 強度模擬技巧且節省觀測成本。本節將驗證敏感區內進行目標觀測的有效性。因為第三節確定的目標觀測最優布局主要覆蓋了一個局地區域，所以我們首先要驗證的是：是否該局地區域的目標觀測較其他局地區域的加密觀測對TC 強度模擬的改善更顯著？另外，與覆蓋范圍更大的非敏感區相比，在敏感區進行相同數目的目標觀測是否對TC 強度模擬的改善也更加有效？最后，在上述揭示的優先觀測時間（或敏感性時間段）和非敏感時間段進行目標觀測是否對TC 強度模擬的改進有顯著差別？為回答這些問題，該研究設計了OSSE-S-III、OSSE-S-IV和OSSE-T-II。

OSSE-S-III 與OSSE-S-I 和-S-II 的不同亦在于OSSE 試驗的第三步。OSSE-S-III 的第三步是在NFSV 型目標觀測敏感區外（或非敏感區）隨機選取20 個與敏感區范圍相當的局地區域，且在每個區域內以90 km 為間隔布置16 個觀測，然后對比同化非敏感區局地區域的觀測和敏感區域的觀測對TC 強度模擬的改善程度。圖1 中12 個TC 個例的OSSE-S-I 模擬結果如圖8 所示。由圖可以看出，同化非敏感區的局地觀測對TC 強度模擬的改善有一定的提高，但都不會優于同化敏感區內目標觀測的效果，而且隨機選取的非敏感區局地觀測區域越接近目標觀測敏感區，同化SST 加密觀測對TC 強度模擬改善程度越高。具體地，圖9 統計了OSSES-III 中所有TC 個例非敏感區局地觀測區域距目標觀測敏感區的距離與TC 強度模擬改善程度的散點圖。結果發現，兩者的相關性達到-0.49，且通過了99%的顯著性檢驗。考慮到不同個例的差異，該研究進一步考察了每個TC 個例中上述兩者的相關性，發現大多數個例中上述相關性更高（如表4所示）。事實上，所有這些結果都強調，由NFSV型SST 強迫誤差所確定的敏感區的目標觀測對于提高臺風強度的模擬水平是最有效的。

圖8 OSSE-S-III 的模擬結果。紅色（藍色）柱為同化小范圍的敏感區（非敏感區）內觀測，對TC 強度模擬的改善情況。“Sen”表示敏感區內進行的OSSE，“I+數字”表示在非敏感區進行的OSSEFig. 8 Results of OSSE-S-III. The red (blue) bars represent the improvement rate of the TC intensity simulation after assimilating the observations in local sensitive (nonsensitive) areas. “Sen” represents the OSSE conducted in the sensitive area，while “I+Number”represents the OSSE conducted in nonsensitive area

圖9 非敏感區的局地觀測距敏感區的距離與TC 強度模擬改善程度的散點圖和線性擬合曲線（紅色實線）。圖中的公式為擬合函數，R 代表相關系數，P 為顯著性水平Fig. 9 Scatter and linear fitting line (the red solid line) between the distance of observations in the nonsensitive area relative to the sensitive area and the improvement of the TC intensity (The formula is the fitting function between the two variables. R and P is the correlation coefficient and the significant level respectively.)

表4 不同個例對應的非敏感區局地觀測距敏感區的距離與TC 強度改善程度的相關系數（ R）Table 4 Correlation coefficients ( R) between the distance of observations in the nonsensitive area relative to the sensitive area and the improvement of TC intensity simulation

上述試驗結果表明，對于在非敏感區內且與敏感區范圍相當的局地區域增加觀測，在敏感區內增加相同數目的觀測能夠更加有效提高TC 強度模擬水平。那么，如果在整個非敏感區覆蓋的大范圍增加觀測，小范圍敏感區的觀測是否在TC 強度模擬的改善中仍具有優越性呢？OSSE-S-IV 可以回答這個問題。在OSSE-S-IV 中，OSSE 試驗的第三步是在大范圍的非敏感區中均勻選取與敏感區內相同的格點數構建模擬觀測，然后對比敏感區局地小范圍觀測與非敏感區的大范圍觀測對TC 強度模擬的改善程度。圖10 展示的是同化了敏感區與非敏感區大范圍觀測后，對模擬的TC 強度的改進情況對比（即OSSE-S-IV 的模擬結果）。可以看到，在相同的觀測數的條件下，同化了敏感區的觀測之后，對TC 強度的改善效果是優于同化了非敏感區的大范圍觀測后的TC 模擬改善效果。由此可見，在SST 目標觀測敏感區內加密觀測，對于提高TC 強度的模擬能力是有效且經濟的。

圖10 OSSE-S-IV 的模擬結果。紅色柱為同化敏感區內觀測對TC 強度的改善程度；藍色柱為同化非敏感區全場的觀測對TC 強度模擬的改善程度。“Sen”代表在敏感區進行的OSSE，“InSen-S”表示在非敏感區全場進行的OSSEFig. 10 Results of OSSE-S-IV. The red bars represent the improvement of the TC intensity simulation after assimilating observations in the sensitive area. The blue bars represent the improvement of the TC intensity simulation after assimilating the same number of observations in the whole nonsensitive area. “Sen” represents the OSSE conducted in the sensitive area, and “InSen-S” indicated the OSSE conducted in the whole nonsensitive area

OSSE-T-II 的試驗步驟與OSSE-T-I 類似，主要在于第五步存在區別。在OSSE-T-II 中，我們分別在敏感性時間段和非敏感性時間段將更新后的海溫強迫場替換對應時間段“真實”的SST 強迫場。圖11 展示的在敏感性時間段和非敏感性時間段進行目標觀測后對TC 強度模擬的改進情況。由圖可以看出，在敏感時間段進行目標觀測改善SST 強迫場對TC 強度模擬的改善具有更大的作用。

圖11 OSSE-T-II 的模擬結果。紅色柱為同化敏感階段的敏感區內觀測對TC 強度的改善程度；藍色柱為同化非敏感階段的敏感區內觀測對TC 強度模擬的改善程度。“Sen-T”代表在敏感區的敏感時段進行的OSSE，“InSen-T”表示在敏感區的非敏感時段進行的OSSEFig. 11 Results of OSSE-T-II. The red bars represent the improvement of the TC intensity simulation after assimilating observations in the sensitive area during the sensitive period. The blue bars represent the improvement of the TC intensity simulation after assimilating observations in the sensitive area during the nonsensitive period. “Sen-T” represents the OSSE conducted in the sensitive area during sensitive period, and “InSen-T” indicated the OSSE conducted in the sensitive area during nonsensitive period

綜上所述，對比小范圍的局地觀測和大范圍的全場觀測，在NFSV 型SST 強迫誤差的前120 個格點區域所確定的目標觀測敏感區內，以適當的間隔布放觀測并同化到海溫強迫場，能夠最大程度地改善TC 強度的模擬效果，尤以NFSV 型SST 強迫誤差大值區所對應的TC 快速增強階段的目標觀測，對TC 強度模擬的改善最為明顯。

5 總結和討論

該研究基于Yao et al.（2021）揭示的對TC 強度模擬結果具有最大影響的NFSV 型SST 強迫誤差，通過OSSE 試驗確定了TC 強度模擬的SST 目標觀測敏感區（即NFSV 型SST 強迫誤差前120個大值點所覆蓋的區域，該區域沿著TC 移動路徑且主要位于TC 的快速增強階段）以及目標觀測的最優觀測時段（即NFSV 型SST 強迫誤差大值區對應的TC 快速增強階段）。研究表明，在上述敏感區及敏感時間段中以90 km 為間隔布放“觀測”并將其同化到WRF 的SST 強迫場，能夠經濟且有效地改善TC 強度的模擬技巧，可能代表了臺風強度模擬的最優海溫目標觀測布局。

為驗證目標觀測敏感區的有效性，該研究設計了三組對比試驗：同化敏感區內“觀測”與同化非敏感區局地區域“觀測”的對比；同化敏感區內“觀測”與同化非敏感區全場“觀測”的對比，以及同化敏感時間段的敏感區內“觀測”與同化非敏感時間段的敏感區內“觀測”的對比。結果表明，同化敏感區內“觀測”對TC 強度模擬的改善效果要普遍要優于同化非敏感區局地區域“觀測”的效果；而且當同化的非敏感區局地觀測的區域越接近目標觀測敏感區時，TC 強度模擬的改善程度越高；特別地，同化小范圍敏感區內“觀測”對TC 強度模擬的改善效果明顯優于同化非敏感區大范圍“觀測”的效果。上述改善尤以NFSV 型SST 強迫誤差大值區所對應的TC 快速增強階段最為明顯。所以，上述根據NFSV 型SST 強迫誤差大值區所確定的最優目標觀測布局及最優觀測時段是有效的，該結果可為臺風的實際外場觀測（如無人潛艇目標觀測）提供科學指導。

如前所述，該研究所選取的TC 個例的移動路徑對海溫強迫擾動并不敏感，所以，這里根據NFSV 型SST 強迫誤差所確定的目標觀測敏感區和最優觀測時段，其目標觀測可能不適用于TC 路徑模擬的改善。另外，TC 強度預報水平的提高依賴于模式的模擬能力，該研究考慮通過目標觀測策略提高SST 強迫場的準確性來改善臺風強度的模擬，這對于具有SST 強迫場的非耦合模式模擬臺風強度水平的提高具有重要意義。事實上，該研究的目標觀測敏感區和敏感時段也對耦合模式模擬臺風強度具有指示意義，即這些敏感性可以告訴模式開發者，如果優先使得耦合模式對上述敏感區和敏感時段的SST 有更好的模擬，那么耦合模式對TC 強度的模擬水平會得到有效改善，進而提高臺風強度的預報水平。