不定積分的求解方法及應(yīng)用

郭 曉，張晨晨

(南陽(yáng)職業(yè)學(xué)院，河南 南陽(yáng) 474500)

不定積分的求解方法是積分問(wèn)題的基礎(chǔ)，本研究結(jié)合例題對(duì)不定積分的各種求解方法進(jìn)行分類(lèi)和總結(jié)歸納，旨在找到最簡(jiǎn)單、最快捷、最有效的解題方法。需要掌握的預(yù)備知識(shí)：設(shè)F(X)與f(x)在區(qū)間I上有定義，若?x∈I，有F′(x)=f(x)或dF(x)=f(x)dx，則稱F(x)為f(x)在區(qū)間I上的一個(gè)原函數(shù)。

1 不定積分

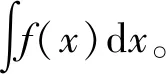
2 不定積分的性質(zhì)

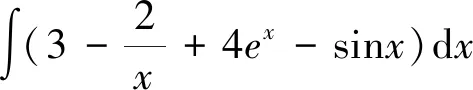
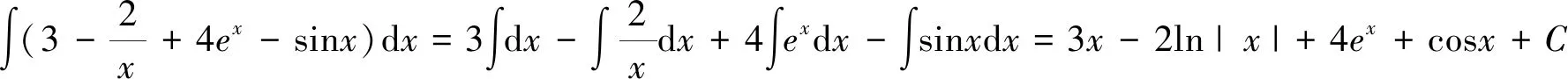
3 基本積分公式

在運(yùn)用直接積分法時(shí)會(huì)用到基本積分公式，下面先給出基本積分公式：

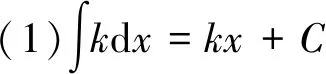
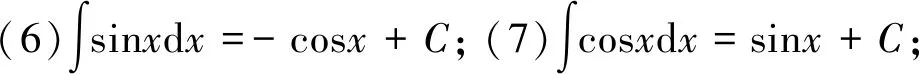
4 直接積分法

在求積分問(wèn)題時(shí)，簡(jiǎn)單的不定積分可以直接利用法則和公式，稍微復(fù)雜的，可以先對(duì)被積函數(shù)做恒等變形，變形成可以利用積分的法則和公式的形式，然后按基本積分公式求出結(jié)果。

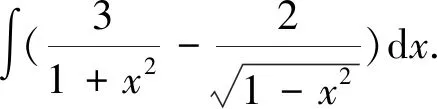
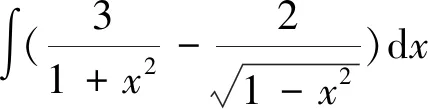
=3arctanx-2arcsinx+C.

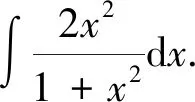
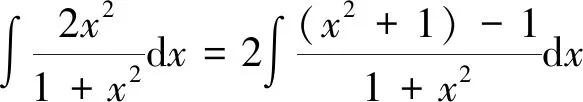
5 換元積分法

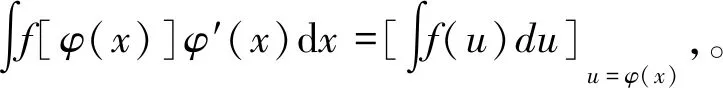
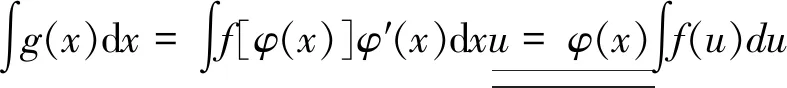
=F(u)+c(積分)=F[φ(x)]+c(回代).

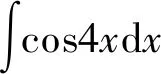
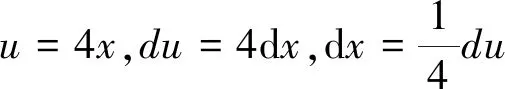
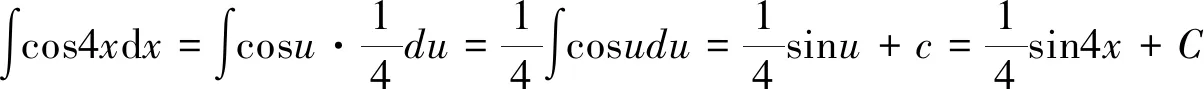
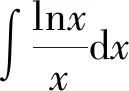
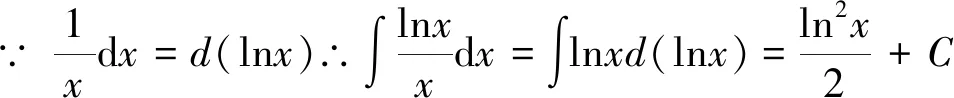
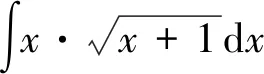
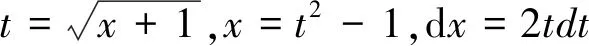
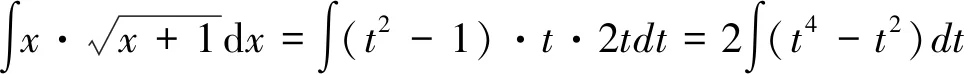
第一類(lèi)換元積分法的關(guān)鍵是如何選取φ(x)， 并將φ′(x)dx湊成微分dφ(x)的形式，因此，第一類(lèi)換元積分法又稱為湊微分法。

在換元積分法中，有一些特殊形式的換元，如：根式代換、三角代換、倒代換。

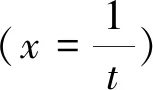
有些不定積分的結(jié)果會(huì)經(jīng)常用到，可作為基本公式：

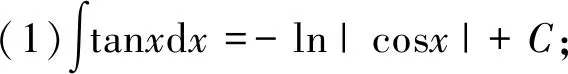
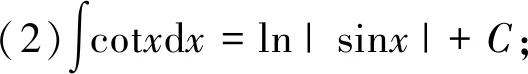
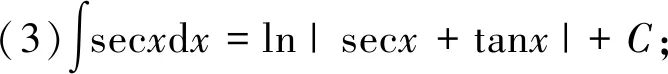
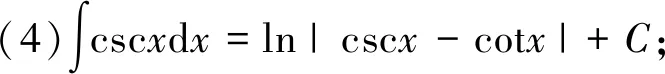
6 分部積分法

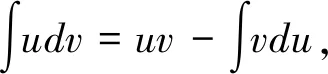
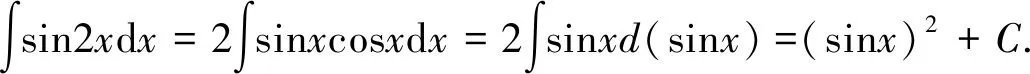
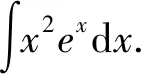
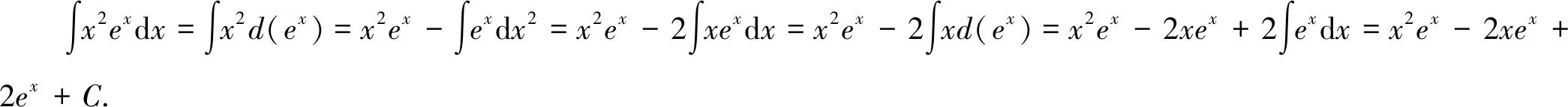
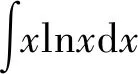
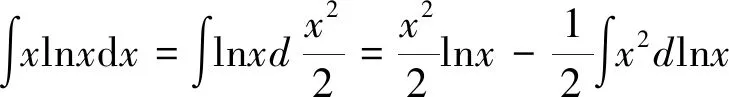
在分部積分法中，u,v的選擇方法可總結(jié)如下：學(xué)生可簡(jiǎn)化記憶，按照反、對(duì)、冪、三、指這個(gè)順序，優(yōu)先選擇前面的函數(shù)為u，另外一個(gè)函數(shù)與dx結(jié)合湊微分，然后運(yùn)用分部積分公式進(jìn)行計(jì)算。

7 結(jié)語(yǔ)

不定積分具有很強(qiáng)的計(jì)算靈活性，學(xué)生需要做大量的練習(xí)，積累更多的經(jīng)驗(yàn)，這樣解起題來(lái)才能得心應(yīng)手。