探究數學本質 培養核心素養
——以一道數列高考試題的探究為例

天津 高成龍

對于“等差乘等比”型數列的前n項和，教材中常用的處理方法是錯位相減法，即通過錯位相減把該類數列的求和轉化為等比數列的求和問題.該方法學生理解起來容易，但是對前n項和Sn進行化簡時會涉及因式分解、合并同類項、提取公因式等煩瑣步驟，另外學生在化簡過程中沒有一個明確的目標，學生甚至不知道化簡到什么程度才是最簡形式，進而給求解帶來很大的障礙.鑒于此種情形，文章用不同的方法對2020年全國卷Ⅲ理科第17題進行多方面的探究，并將解法推廣至一般情形，得到了等差乘等比數列前n項和的三個常用模型：“裂項求和模型”“待定系數模型”和“導數模型”.這樣通過建立模型就可以把該類數列的求和問題轉化為數學模型問題，實現數列問題模型化.這一過程很好地培養了學生運用數學模型解決數列問題的能力，同時也可以幫助教師很好地進行教學反思和提升教師的專業素養.

一、試題呈現及評析

【例】(2020·全國卷Ⅲ理·17)設數列{an}滿足a1=1,an+1=3an-4n.

(1)計算a2,a3，猜想{an}通項公式并加以證明；

(2)求數列{2nan}前n項和Sn.

【試題評析】(1)主要考查數列的遞推關系，易得an=2n+1；(2)以等比數列的求和模型為背景，求等差乘等比數列的前n項和，這是一個綜合情境，解決問題的關鍵是利用錯位相減法將不能直接求和的數列轉化為等比數列的前n項和，這一過程可以很好地培養學生在綜合情境中提出運算問題和確定運算對象的能力，進一步提升學生的數學運算素養.下面分別運用錯位相減法、累加法、裂項相消法、導數法、面積法對(2)的解題方法進行探究.

二、試題解法探析

思路1：錯位相減法

設cn=(2n+1)·2n，

Sn=3×21+5×22+7×23+…+(2n+1)2n，

2Sn=3×22+5×23+7×24+…+(2n-1)2n+(2n+1)2n+1，兩式相減，得

-Sn=6+2(22+23+…+2n)-(2n+1)×2n+1

=6+8(2n-1-1)-(2n+1)2n+1

=-2-(4n-2)2n，

解得Sn=2+(4n-2)2n.

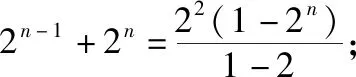
思路2：累加法

設cn=(2n+1)2n，則cn+1-cn=(2n+3)2n+1-(2n+1)2n=(2n+5)2n=cn+2n+2，

c2-c1=c1+23，

c3-c2=c2+24，

……

cn+1-cn=cn+2n+2，

累加得cn+1-c1=Sn+(23+24+…+2n+2)=Sn+8(2n-1)，

解得Sn=2+(4n-2)2n.

【評注】累加法是數列求和中的常用方法，通過累加法把等差乘等比數列的求和問題轉化為等比數列的求和與解一元一次方程，它與錯位相減法的本質是一樣的.

思路3：裂項相消法

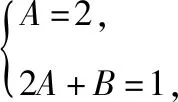
于是F(n)=(2n-3)2n，于是Sn=c1+c2+c3+…+cn=F(n+1)-F(1)=2n+1(2n-1)-2(2-3)=2n(4n-2)+2.

【評注】應用裂項求和法的關鍵是根據通項公式的特點先把數列cn進行等價變形寫成F(n+1)-F(n)的形式，最后利用函數恒等式的原理求得F(n)的解析式，裂項求和法的實質是對數列作等價變形.

思路4：導數法

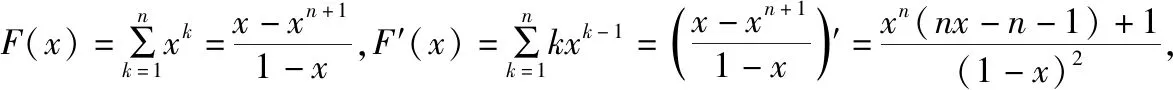
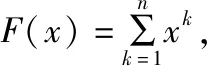
思路5：面積法

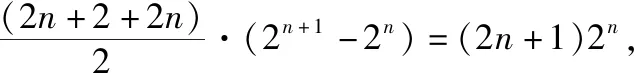
分別過點P1,P2,…，Pn,Pn+1作y軸的垂線，垂足分別為H1,H2,…，Hn,Hn+1，

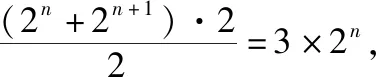
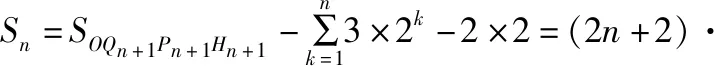
【評注】應用面積法求解數列問題思路比較新穎，方法十分巧妙，該思路來源于2017年山東省高考數學第19題.應用面積法的關鍵是根據數列通項公式的特點去構造n+1個動點，進而形成n個直角梯形，使得第n個直角梯形的面積恰好等于該數列的通項.該方法可以讓學生從幾何圖形的角度去體會“等差乘等比”型數列前n項和的幾何意義，真正實現“代數運算與幾何直觀之間的融合”，這也是《普通高中數學課程標準(2017年版2020年修訂)》(以下簡稱《課程標準》)對幾何與代數主題的要求.

三、試題拓展

1.“等差乘等比”型數列求和探究

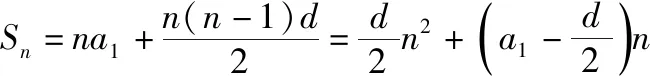
模型1(裂項求和模型)：若數列{an}的通項an=(an+b)qn(q≠1)，則其前n項和模型為Sn=F(n+1)-F(1),其中F(n)=(An+B)qn，A,B可以由a,b唯一確定.

證明：設F(n)=(An+B)qn，則F(n+1)=(An+A+B)qn+1，

an=F(n+1)-F(n)=(Aqn+qA+qB-An-B)qn=(an+b)qn，

模型2(待定系數模型)：若數列{an}的通項為an=(un+v)qn(q≠1)，則其前n項和模型為Sn=A+qn(Bn-A)，其中A,B為常數，可以由a1,a2唯一確定.

證明：由裂項求和模型得，Sn=F(n+1)-F(1)，其中F(n)=(un+v)qn，u,v可以由a1,a2唯一確定，所以

Sn=F(n+1)-F(1)=(un+u+v)qn+1-(u+v)q=qn(uqn+uq+vq)-(uq+vq),

令-(uq+vq)=A,uq=B則Sn=A+qn(Bn-A)，其中A,B為常數，可以由a1,a2唯一確定.

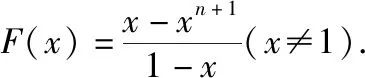
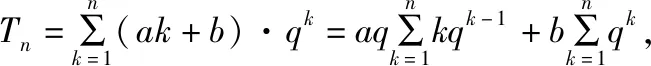
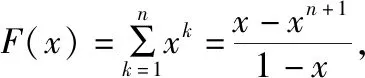
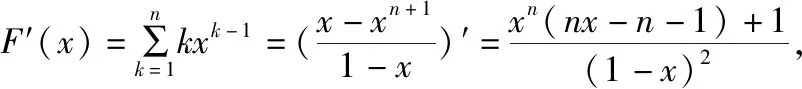
所以Tn=aqF′(q)+bF(q).

2.“等差乘等比”型數列求和模型拓展

模型2說明了等差乘等比數列的前n項和公式為Sn=A+(Bn-A)qn，其中A,B為待定系數，可以利用a1,a2唯一求得.事實上,可以將等差乘等比數列中的等差數列推廣到關于n的任意次多項式，即

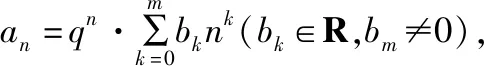
四、等差乘等比數列求和模型在高考中的應用

1.2016至2021年高考中的“等差乘等比”型數列統計

“等差乘等比”數列在高考中出現的頻率較高，現對2016至2021年高考中的等差乘等比數列的題型與分值進行統計，可以得到：

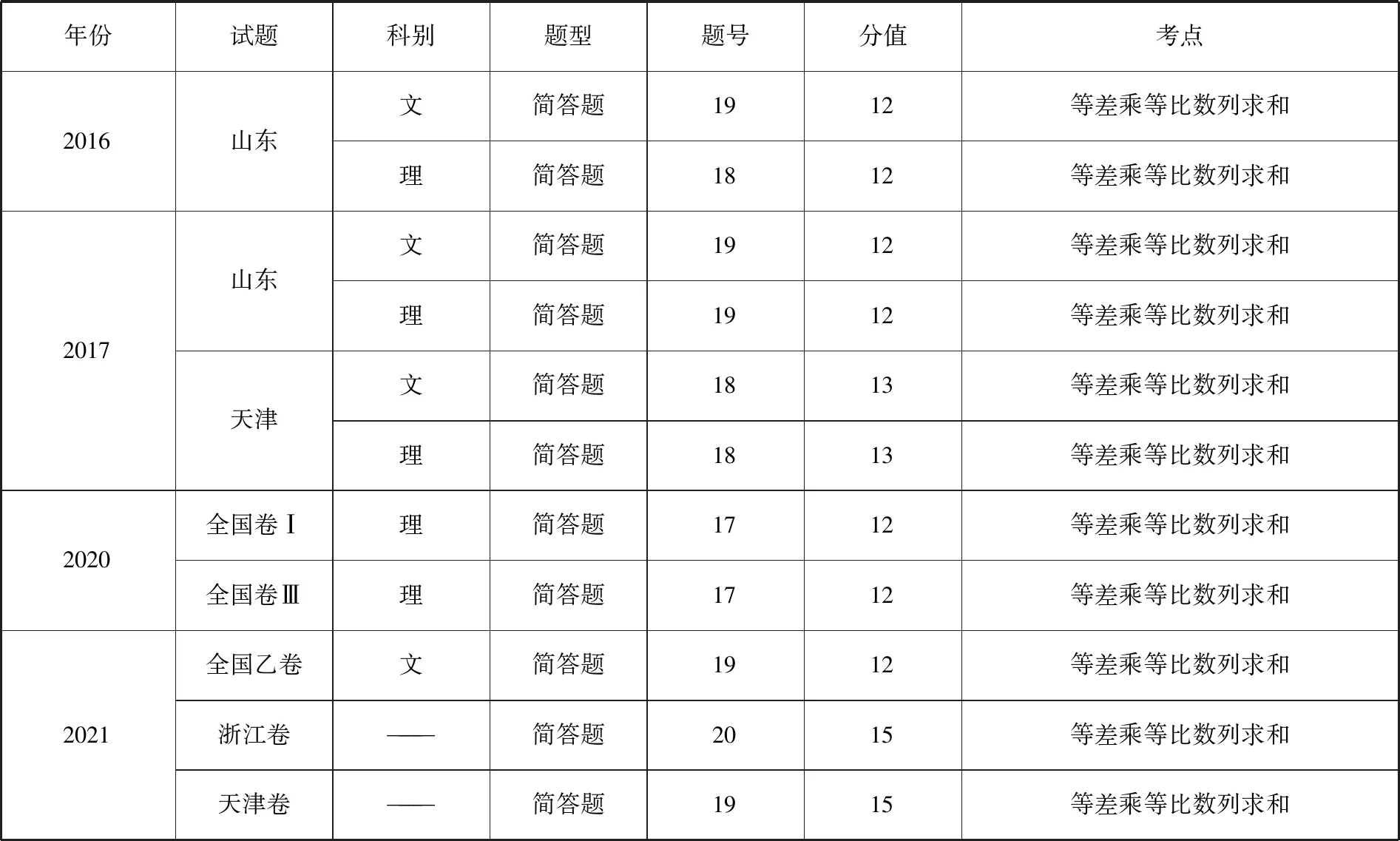
年份試題科別題型題號分值考點2016山東文簡答題1912等差乘等比數列求和理簡答題1812等差乘等比數列求和2017山東天津文簡答題1912等差乘等比數列求和理簡答題1912等差乘等比數列求和文簡答題1813等差乘等比數列求和理簡答題1813等差乘等比數列求和2020全國卷Ⅰ理簡答題1712等差乘等比數列求和全國卷Ⅲ理簡答題1712等差乘等比數列求和2021全國乙卷文簡答題1912等差乘等比數列求和浙江卷———簡答題2015等差乘等比數列求和天津卷———簡答題1915等差乘等比數列求和

2.“等差乘等比”型數列求和模型在高考中的應用

下面以2021年全國乙卷文科第19題為例來說明“待定系數模型”“裂項求和模型”“導數模型”在解決等差乘等比數列前n項和中的應用.

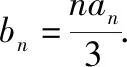
(1)求{an}和{bn}的通項公式；

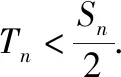
思路1：待定系數模型

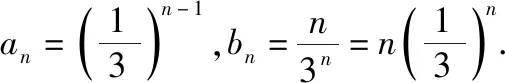
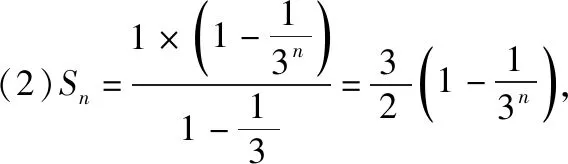
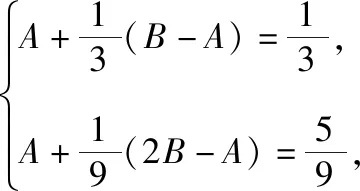
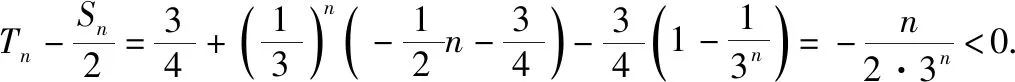
思路2：裂項求和模型

由bn=F(n+1)-F(n)得，

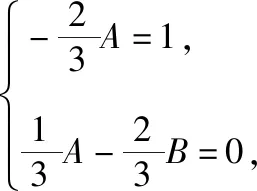
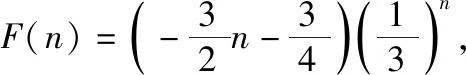
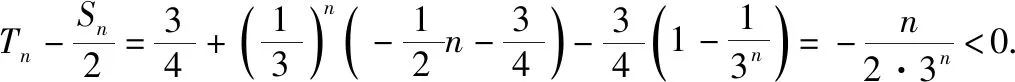
思路3：導數模型

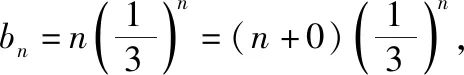
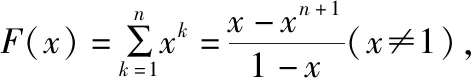
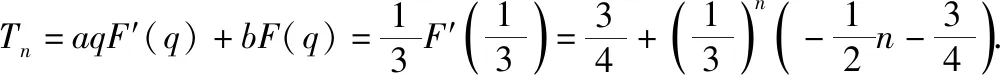
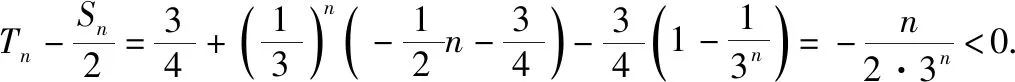
五、素養展現與方法反思

1.素養展現

文章從一道高考題目出發用不同的方法對“等差乘等比”型數列的求和進行了深入探究，給出了該類數列前n項和的三個模型，體現了特殊到一般的數學思想，同時這一過程還可以很好地培養和提升學生的數學素養.具體表現為①題目是以等比數列的求和模型為背景，求等差乘等比數列的前n項和，這是一個綜合情境，解決問題的關鍵是利用錯位相減法不能直接求和的數列轉化成等比數列的前n項和，這一過程可以很好地培養學生在綜合情境中提出運算問題和確定運算對象的能力，進一步提升數學運算素養；②在實際教學中通過五種思路的比較，讓學生感受到運用求和模型求解該類數列前n項和的優勢，同時五種思路能讓學生從不同的層面、不同角度入手去研究“等差乘等比”型數列的前n項和問題，培養學生根據問題特點及運算的條件合理選擇運算方法的能力，進一步提升數學運算素養；③運用三種求和模型求解“等差乘等比”型數列的前n項和問題，可以促進學生對函數模型多樣性的理解；④運用函數模型求解等差乘等比數列前n項和，體現了數列是一種特殊的函數，在數列教學中應該培養學生運用函數模型解決數列求和問題的能力，從函數的角度去研究數列，讓學生感受數列與函數的共性與差異，體會數學的整體性，這也是《課程標準》對數列部分的要求.

2.方法反思

學生運用錯位相減法求解等差乘等比數列的前n項和問題時，對Sn進行化簡時會涉及因式分解、合并同類項、提取公因式等煩瑣步驟，進而給求解帶來很大的障礙，究其原因，主要是學生在化簡過程中沒有一個明確的目標，甚至不知道化簡到什么程度是最簡形式，而模型2正好為化簡提供了方向和目標.因此，學生在求解該類數列前n項和時，無論是選擇錯位相減法，還是裂項求和模型、待定系數模型、導數模型，其最終結果均是A+(Bn-A)qn的形式，這也體現了等差乘等比數列前n項和的對稱美.