對兩道原創試題的一點探討

湖北 許 文

筆者曾經多次參加原創試卷的命審題工作，深感原創試卷的設計與命審題是一項十分嚴謹和細致的工作。雖然一套原創試題的定稿，經過了命題組老師的精心設計，審題組老師的多次審查，對每道試題逐字逐句的打磨，經過小范圍內試做，根據試做反饋意見再修改等多個環節，但即便如此，也很難做到十全十美。還可能存在試題條件是否符合實際，設計的問題情境是否真實等問題。本文對兩道原創試題進行一點探討。

一、問題條件應符合實際

問題條件是試題分析與求解的關鍵。原創物理試題應符合實際的物理情境，給出的條件應嚴謹、科學，不能憑空想象。

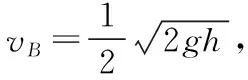
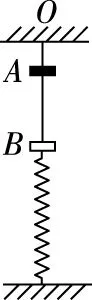
圖1

(1)A、B物塊碰撞后的共同速度v；

(2)彈簧的勁度系數k；

(3)若改為t=0時剪斷A、B兩物塊間的細繩，其他條件不變，選取豎直向上為正方向，寫出B物塊的振動方程。

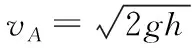
A、B碰撞過程，由動量守恒定律有：

2mvA+mvB=(2m+m)v

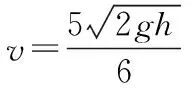
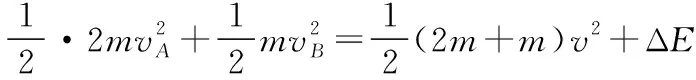
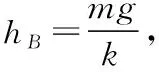
ΔE=2mg(h-hB)

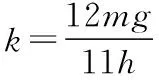
(3)若改為t=0時剪斷A、B兩物塊間的細繩，物塊B在豎直方向做簡諧振動，其振幅為A=hB，周期為T，由題意有：

選取豎直向上為正方向，B物塊的振動方程為：

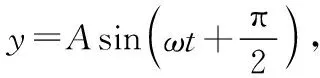
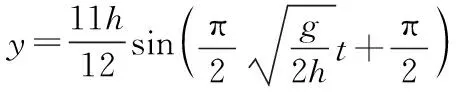
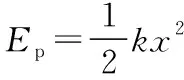
碰撞前對A物塊，由機械能守恒定律有：

對兩物塊的碰撞過程，由動量守恒定律有：

2mvA+mvB=(2m+m)v(2)

碰撞后兩物塊運動的最高點為B物塊的初始位置，碰撞后兩物塊與彈簧組成的系統機械能守恒，有：

或者在兩物塊碰撞前，由物塊B與彈簧組成系統機械能守恒，有：

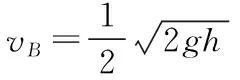
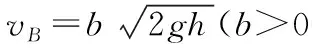
將(6)(7)兩式代入(3)(4)(5)三式中，聯立解得：

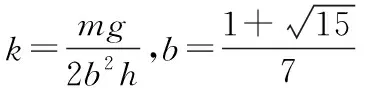
[注：可得15b2=(2+b)2]

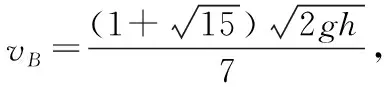
二、運動過程應嚴謹科學

一個物理問題的發生與發展應經歷一定的物理過程。同一問題即使在相同的條件下，經歷不同的物理過程，可能會出現不同的結果。我們在原創命題時要重視試題中物理過程的多變性，問題情境的嚴謹性與科學性。

【試題2】(多選)如圖2所示，在平面直角坐標系xOy的x軸上方的部分區域存在著磁感應強度大小為B、方向垂直紙面向里的勻強磁場，在x軸的負方向上放置有熒光屏，在坐標原點O處有一粒子源，粒子源向第一象限內均勻發射大量的速率為v、比荷為k的帶正電的粒子，若所有的粒子均垂直打在熒光屏上，則下列判斷正確的是

( )

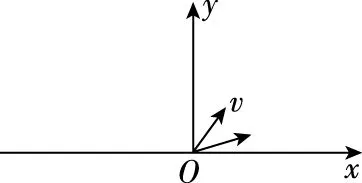
圖2

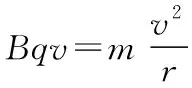
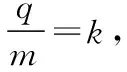
設某一粒子射出磁場時的坐標為(x，y)，此時粒子的速度方向垂直x軸(如圖3)，

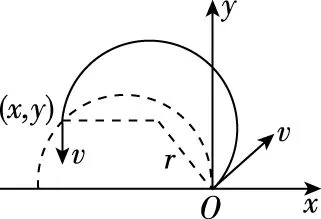
圖3

則有：(-x-r)2+y2=r2，即(x+r)2+y2=r2

可知從半圓弧(x+r)2+y2=r2(y≥0)射出磁場時粒子的速度方向垂直x軸。

故最小的磁場范圍應是如圖4所示的三段圓弧所圍成的陰影部分區域。

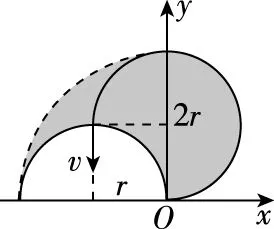
圖4

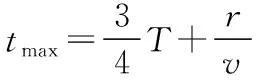
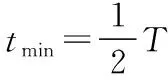
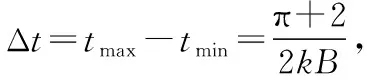
【探討】以上命題老師給出的解析，似乎無懈可擊。但試題中設置了求磁場的最小區域問題，那么關于帶電粒子在磁場中的運動情境就變得不太嚴謹。

事實上，要實現試題中帶電粒子的偏轉運動，帶電粒子有可能不是一直在磁場中做連續的圓弧偏轉運動直到離開磁場時速度方向垂直于x軸。從O點發射的粒子有可能先在磁場中做一段圓弧運動后離開磁場，然后從某處再次進入磁場中做圓弧運動，直到離開磁場時速度方向垂直于x軸。如“磁聚焦”與“磁發散”的運動情境可以實現試題中對帶電粒子的偏轉要求的結果。

設帶電粒子從O點射入第一象限的部分磁場區域，在第一象限內某點(x，y)處射出磁場時速度方向沿y軸正方向。有：(r-x)2+y2=r2，即第一部分磁場區域上邊界滿足方程：(x-r)2+y2=r2；下邊界滿足方程：x2+(y-r)2=r2；兩式中x、y分別滿足條件：0≤x≤r，0≤y≤r。

當所有粒子的速度沿y軸正方向從直線y=r處再次射入相同的第二部分磁場中，粒子只需在磁場中再運動半個圓周，再次經過直線y=r處射出第二部分磁場時，所有粒子的速度方向均沿y軸負方向，即可垂直打到放置在x軸上的熒光屏上，以實現題目對帶電粒子偏轉要求的結果，這時最小的磁場區域如圖5陰影部分所示。

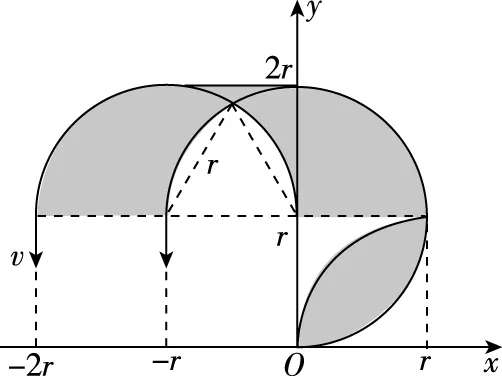
圖5

由幾何知識與對稱性知，圖5陰影部分所示的磁場區域面積為：

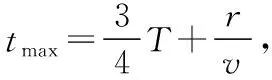
對于帶電粒子在勻強磁場中的圓弧運動，僅憑粒子的初始條件與最后結果推理其運動情境是不夠的，因為不同的磁場區域設計使得粒子的偏轉運動過程具有不確定性。為使粒子的運動過程嚴謹、科學，我們在原創命題時可作適當的條件限定，如本試題可將題干中“x軸上方的部分區域存在著……”改為“x軸上方由三段圓弧組成的部分區域內存在著……”，加了這樣的限定，那么最小的磁場區域就可能是命題人原解析中給出的答案，試題就更嚴謹、科學了。