帶電粒子在電磁組合場中運動規律探討
——對2021年全國高考物理甲卷第25題的深入剖析

安徽 王偉民 楊培軍

帶電粒子在磁場、電場特別是二者組合場中的運動規律問題，是近幾年物理高考的熱點問題，幾乎每年的高考試卷都有此類問題出現，而且大多是綜合性較強的計算題，在整個試卷中所占分值比例往往較高。這類綜合性問題，可以考查學生對洛倫茲力、電場力、拋體運動、圓周運動等知識點的掌握情況，還可以考查學生綜合運用物理知識解決復雜問題的能力。剛剛過去的2021年全國高考物理甲卷也是如此，下面的例題1就是該試卷的壓軸題，單題分值高達20分。

一、原題呈現

【例1】(2021·全國甲卷第25題)如圖1，長度均為l的兩塊擋板豎直相對放置，間距也為l，兩擋板上邊緣P和M處于同一水平線上，在該水平線的上方區域有方向豎直向下的勻強電場，電場強度大小為E；兩擋板間有垂直紙面向外、磁感應強度大小可調節的勻強磁場。一質量為m，電荷量為q(q>0)的粒子自電場中某處以大小為v0的速度水平向右發射，恰好從P點處射入磁場，從兩擋板下緣Q和N之間射出磁場，運動過程中粒子未與擋板碰撞。已知粒子射入磁場時的速度方向與PQ的夾角為60°，不計重力。

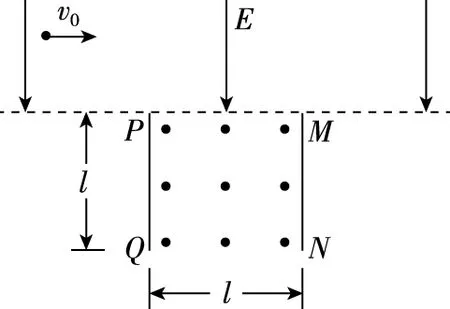
圖1

(1)求粒子發射位置到P點的距離；

(2)求磁感應強度大小的取值范圍；

(3)若粒子正好從QN的中點射出磁場，求粒子在磁場中的軌跡與擋板MN的最近距離。

二、試題評析

該題目共設置三個問題，三個問題彼此獨立，考查的知識點全面而不重復，各問題的解決互不影響，這樣可以避免考生因為前面的問題無法求解而影響后續問題解答的現象發生，使得試題的區分度更加的精細準確。否則，如果題目設置的多個問題互相牽連，前面問題的答案是解決后續問題的條件，那么，具有解答后續問題能力而前面問題沒能正確解答的考生，做這樣的題目將無法得分，這樣對知識點掌握不全面和完全沒掌握的考生就無法形成區分。

從考生反饋的消息來看，三個問題的難度也不相同，相比而言，第一個問題難度最大，考生只有熟練且靈活掌握平拋運動的規律和相關公式(包括運動學、動力學、電磁學的相關公式)，才有可能解決這個問題；第三個問題相對難度最低，但也需要考生具有正確判斷帶電粒子運動軌跡能力的同時，還要具有綜合運用數學知識解決復雜物理問題的能力。

由此可見，本題目考查的知識點全面而有梯度，具有拉開不同水平和能力的考生分數差距的作用，這也是作為選拔性考試的試卷所必須具備的一個條件。

三、題目變式

帶電粒子在電場與磁場的組合場中運動時，涉及電場強度、磁場強度、粒子質量、粒子電荷量、粒子的運動速度、軌跡圓的半徑等諸多物理量以及有界電場或磁場的邊界形狀等條件，將這些物理量和相關條件作為常量或變量進行不同組合，可以歸納出種類繁多的問題，適合于編擬難度較大，技巧性較高的綜合性推理計算或證明題目，此類問題大多需要結合數學知識方能解決，可以全面考查學生分析問題和解決問題的能力。如果我們以上面例題1給出的材料背景為藍本，更改相關條件之后，可以將其改編為與原高考題目物理背景相似的變式題目。

由原高考題目條件可知，帶電粒子在上方電場中的運動為類平拋運動，而它以一定速度由上方的電場進入下方磁場后的運動是勻速圓周運動，受電場和磁場邊界形狀的影響，粒子在組合場中的運動軌跡是一段拋物線與一段圓弧組合成的曲線。如果我們將題目對磁場的限制條件——磁場是“磁感應強度大小可調節的勻強磁場”更改為“磁場方向可作周期性變化的勻強磁場”，并限定其變化周期，那么帶電粒子由上方的電場進入下方的磁場之后，它的運動軌跡將變得復雜起來，不再是原來的一段圓弧，而是多個相切的圓弧，這個問題的解決也將變得相對復雜。

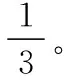
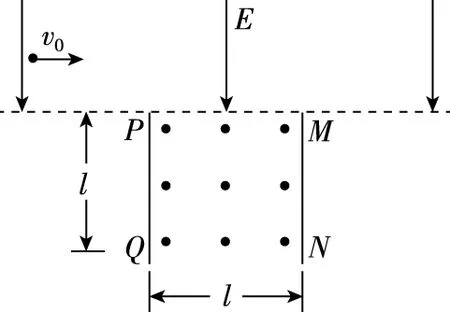
圖2

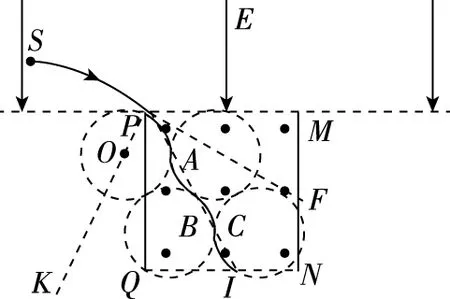
圖3

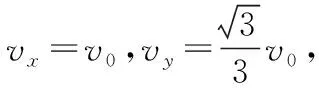
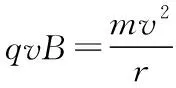
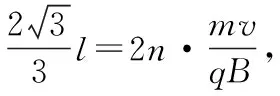
對原高考題目而言，為了使問題簡化，題目限定了帶電粒子的運動范圍——“運動過程中粒子未與擋板碰撞”，而且粒子是“從兩擋板下緣Q和N之間射出磁場”，所以帶電粒子在磁場中的運動軌跡只能是一段圓弧。實際上，在不考慮粒子重力影響的情況下(不論是跟電場力、磁場力相比，還是跟粒子與擋板的作用力相比，在場強較大時，粒子的重力都是相對非常小的，通常可以忽略不計)，粒子與光滑擋板碰撞后的運動，其速度方向的改變也遵從光的反射定律，即反彈前后帶電粒子的運動方向與擋板的夾角相等。因此，如果我們改變題目條件，人為的設定條件讓粒子在磁場中與光滑擋板碰撞，那么，粒子在磁場中的運動軌跡也將不再是原來的一段圓弧，而是多段圓弧組合而成的曲線，這樣一來，跟原來高考題目問題的求解過程相比，就需“額外”應用圓與圓之間的關系等幾何知識，相關物理問題的解決難度也會相應增加。

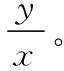
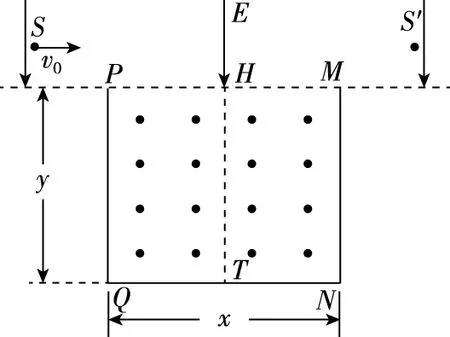
圖4

【分析】不計粒子重力時，帶電粒子在有界磁場中的運動軌跡是圓或圓上的一部分(即圓弧)。由題目條件可知，帶電粒子的運動分三個階段——先在上面的電場中做類平拋運動，之后進入下面的磁場，在磁場中由于跟擋板撞擊后再反彈，粒子沿一系列圓弧軌跡運動，最后由下面的磁場進入上面的電場做類斜拋運動。由于P、M關于HT對稱，S、S′也關于HT對稱，所以，粒子在M點離開磁場進入電場時的速度方向所在的直線，與它在P點由電場進入磁場時的速度方向所在的直線也關于HT對稱。用反證法可以證明，帶電粒子與擋板的4次碰撞的分布，只可能是與兩個豎直擋板各碰撞一次，與底部的水平擋板碰撞2次，所以，粒子在磁場中的運行軌跡如圖5所示。圖5中只畫出了粒子在磁場中的運動軌跡，粒子在上面電場中的運動軌跡沒有畫出。

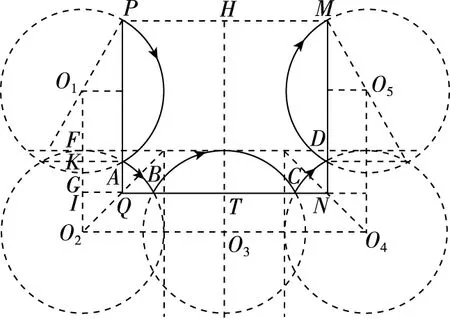
圖5

【解析】帶電粒子在磁場中經過各擋板反彈后運動時，由于碰撞過程沒有能量損失，所以，粒子在磁場中運動的速度大小保持不變，運動軌跡是半徑相等的一系列圓弧，設圓弧的半徑為r，圖5中A、B、C、D是粒子在磁場中四次碰撞的反射點，易知，圓弧PA所對的圓心角為120°，所以：

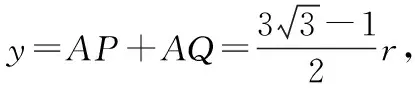
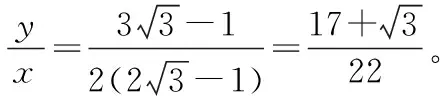
四、結語

帶電粒子在電場和磁場形成的組合場中的運動，規律相對比較復雜。對帶電粒子在組合場中運動規律的探討，往往涉及多個物理知識點，問題的解決大多牽扯到很多物理公式，綜合性很強，解決此類問題需要學生具有較強的分析問題和解決問題的能力，歷年高考中，編者常將這類問題編擬為區分考生能力高下的壓軸題的做法也就不足為奇了。

對原創題目進行改編是理科教師應該具備的一項基本技能。對于帶電粒子在組合場中的運動問題，因為涉及的條件往往很多，可以改變條件與問題的組合進行變式改編，也可以將某個已知條件進行適當變化，如更改磁場或電場的邊界形狀，更改磁場或電場強度及方向的變化規律等，正所謂牽一發而動全身，當題目條件改換時，題目背景可能會發生質的改變。對一些高考原創題目進行改編，能夠得到與原高考題目背景材料相似的變式題目，通過這樣的改編，可以使我們對題目的條件與結論之間的邏輯關系，以及各并列條件之間的自洽關系有更為深入的理解。