新陳代謝GM(1，1)模型在滑坡預測中的應用

陳 曦

(成都理工大學 地球科學學院，四川 成都 610059)

滑坡是分布最廣的地質災害之一，我國滑坡易發區域占國土的2/3，滑坡的危害性極大。滑坡的監測預測顯得尤為重要，對于滑坡災害進行直接監測和準確預測，能夠提早采取相應防災、減災、救災措施，將滑坡災害可能會造成的損失降到最低。滑坡位移的預測可為滑坡預警及后續防災、減災、救災工作提供正確的數據和重要決策依據[1-3]。

將滑坡位移變化視作隨時間變化的灰色過程[4，5]，利用灰色預測模型描述滑坡位移變化趨勢。傳統GM(1，1)模型預測分析數據具有較強的指數性，對于變化較大的滑坡位移序列預測效果不是很好[6]。筆者建立新陳代謝的GM(1，1)模型，利用擬合區間滑動的方法，動態預測滑坡位移序列，并結合滑坡位移實例數據對模型進行驗證。

1 主要方法

1.1 GM(1，1)模型

滑坡位移序列經過級比驗證和數據處理才能建模[7，8]。

設原始序列為x(0)=(x(0)(1)，x(0)(2)，…，x(0)(n))，n為位移期數，計算位移序列級比：

δ(i)=x(0)(i-1)/x(0)(i)，(i=1，2，3，…，n)

(1)

當所有δ(i)都處于(e-2/(n+1)，e2/(n+1))內時，符合級比驗證可建模。如果不符合，需要進行數據平移，計算平移后的新序列再進行級比驗證y(0)(n)=x(0)(n)+K，K為數據平移常數。

設滑坡位移原始位移序列為x(0)，各原始序列為：

x(0)=(x(0)(t))，t=1，2，…，n

(2)

一次累加序列為：

x(1)=(x(1)(t))，t=1，2，…，n

(3)

(4)

x(1)的緊鄰均值序列為：

(5)

對位移數建立微分方程：

(6)

微分方程離散化為：

x1(0)(t)+az1(1)(t)=b

(7)

構建矩陣：

(8)

(9)

其中，B為系數矩陣，Y為常數向量。

根據最小二乘法求解系數：

(10)

微分方程時間響應式為：

(11)

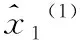
(12)

根據式(12)，可預測后續位移。

1.2 新陳代謝GM(1，1)預測模型

當利用傳統GM(1，1)模型預測時，是將樣本數據全部擬合以建立灰色變化模型[9，10]，這樣可以描述樣本整體的變化情況，并根據變化趨勢預測后續位移變化，但對于非指數性的滑坡位移序列，傳統GM(1，1)模型在進行預測時，不能動態更新預測期數前的實際值，所有預測結果均使用同一段舊信息位移，因此對預測期數中產生局部變化的地方描述能力較弱，不能很好地擬合真實變化曲線。針對這個問題，筆者建立一種新陳代謝的GM(1，1)模型，以滑動窗口作為樣本區間，通過建模樣本序列首尾不斷更替的方式完成新陳代謝，以新陳代謝區間進行建模預測的結果不僅能更好地反映滑坡位移的局部變化，也能與整體變化曲線有很高的擬合優度。

新陳代謝GM(1，1)模型實現方法為[11，12]：

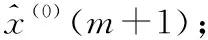
1.3 模型精度檢驗

計算原始序列和預測殘差序列的方差：

(13)

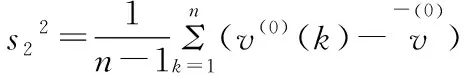
(14)

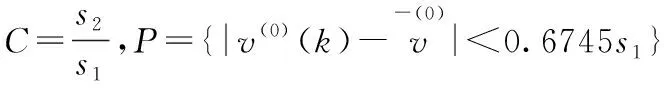
(15)

表1 灰色模型預測精度參照

2 實驗分析

筆者以福寧八尺門滑坡監測位移數據為例，來驗證所建立新陳代謝GM(1，1)滑坡位移預測模型的精度。滑坡實例位移數據一共60期，數據來源于國家科技基礎條件平臺—國家地球系統科學數據中心(http://www.geodata.cn)。由于在建立GM模型過程中，需要計算緊鄰均值，時間響應式中也需要序列第一個數值帶入模型，所以至少需要3個位移數據組成樣本序列。因此，樣本區間信息數量分別設置為3、4、5、6、7、8，對比不同樣本區間設置下的預測精度，為了統一比較預測精度，所有樣本區間預測均從第9期開始，預測第9-60期位移數據。原始滑坡位移第9-60期數據作為精度驗證數據集。由于儀器觀測精度和環境因素的影響，觀測得到的滑坡形變序列會因擾動存在誤差，因此利用多項式模型對滑坡位移數據進行擬合，通過將離散數據回歸到正常變化曲線，除去滑坡位移中噪聲項的影響，使預測精度更高。不同樣本區間預測精度如表2所示。

表2 不同樣本區間預測精度

由表1可知，對照灰色模型預測精度參照表，樣本區間為3、4、5、6的預測模型屬于一級精度模型，預測效果最好；樣本區間選擇7時預測模型的后驗方差比介于0.5和0.65之間，為二級精度模型；樣本區間為8時，后驗方差比大于了0.65，為四級精度模型，預測效果較差。在一級精度模型中，區間為3時后驗方差比最小，因此選擇樣本區間為3，建立新陳代謝GM(1，1)預測模型，同時建立傳統GM(1，1)預測模型，對比兩種模型預測結果，驗證筆者所建立模型的預測效果。模型的預測結果曲線如圖1所示。

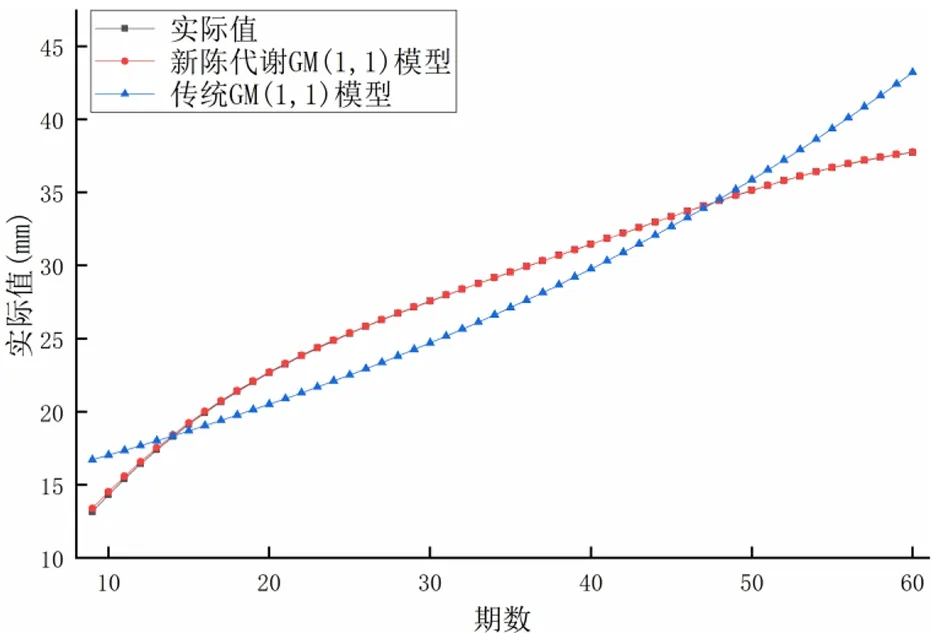
圖1 模型預測結果

由圖1可知，各模型預測曲線對比反映，新陳代謝GM(1，1)模型預測結果與實際值曲線較為重合，預測變化趨勢比較符合實際變化；傳統GM(1，1)模型預測結果雖然總體增長趨勢與實際值近似，但預測呈指數性質，與實際值相差較大。

為準確評估滑坡預測效果，選取均方根誤差RMSE、平均絕對誤差MAE和平均相對誤差MRE，對兩種模型預測結果進行評價。

計算得到新陳代謝GM(1，1)模型預測結果的MAE為0.0403mm，RMSE為0.0648mm，MRE為0.0021。傳統GM(1，1)模型預測結果的MAE為2.057mm，RMSE為2.365mm，MRE為0.077。相比傳統GM(1，1)模型，筆者所建立的新陳代謝GM(1，1)模型的預測MAE提高了98%，RMSE提高了97.2%，MRE提高了97.3%。新陳代謝GM(1，1)模型預測精度較高，對GM(1，1)模型的改進有一定的效果。

3 結論

筆者以福寧滑坡監測數據為例，建立新陳代謝GM(1，1)預測模型對滑坡位移進行預測研究。利用新陳代謝GM(1，1)預測模型不斷更新新信息和去除舊信息的優勢，以最大程度趨勢逼近位移的真實變化，預測滑坡位移。與傳統GM(1，1)模型對比預測精度，結果表明新陳代謝GM(1，1)滑坡位移預測模型精度更高，預測結果的平均絕對誤差達到0.0403mm，均方根誤差為0.0648mm，平均相對誤差為0.0021，預測位移結果更符合實際位移值變化，對于滑坡預測預警有一定的意義和價值。