捷聯相控陣雷達導引頭視線角速率估計技術

韓旭東，張鵬飛，張 意，齊竹昌，柴 勁

(西安現代控制技術研究所，西安 710065)

0 引言

相控陣雷達導引頭采用全主動的探測方法，體積小、作用距離遠、探測精度高、抗干擾能力強，適合復雜的戰場環境，可使末制導彈藥真正實現“發射后不管”；而捷聯體制使導引頭具備一定的低成本發展空間，可適應更高的發射過載，因此捷聯相控陣雷達制導是制導彈藥領域未來發展的重要方向。捷聯相控陣雷達導引頭(簡稱捷聯相控陣導引頭)無法直接提供彈目視線角速率，因此對視線角速率進行濾波提取是捷聯相控陣制導的關鍵技術之一。

1 捷聯相控陣導引頭視線角速率提取

捷聯相控陣導引頭通過波控計算機控制移相器相位來實現對波束指向的控制，從而代替了傳統的隨動機械式掃描[1]，可直接測量的目標參數包括：目標相對于彈體的視線角即體視線角、彈目相對距離以及彈目相對速度等。制導計算機需利用慣性導航系統提供的姿態信息構建“數字解耦平臺”，從耦合了彈體姿態信息的體視線角中獲得彈目視線角，并通過合適的濾波算法估計出制導系統所需的彈目視線角速率。當前，國內外學者就視線角速率的估計方法做了大量研究，文獻[2-6]主要應用了以下3種方法：

1)基于“坐標轉換”構建“數學解耦平臺”。即制導計算機利用慣性導航系統提供的彈體姿態角，將導引頭測得體視線角解耦為慣性視線角，并采用微分濾波器得到彈目視線角速率[2]。此方法適用于激光半主動、圖像、雷達等各種捷聯體制的末制導中，其解耦精度主要依賴于姿態角及體視線角的測量精度，因而對慣性導航系統及導引頭的測量精度要求較高。

2)在捷聯相控陣制導方面，文獻[3]基于相控陣波束穩定控制回路獲取彈目視線角速率。利用捷聯相控陣導引頭實時測量的失調角，慣性導航系統提供的彈體姿態角，產生波束角的控制指令以消除導引頭失調角，該控制回路在實現波束對目標穩定跟蹤的同時，也可產生彈目視線角速率，彈載計算機不必對其進行求取，該方法節省了彈上計算資源。

3)基于非線性卡爾曼濾波器估計彈目視線角速率。建立彈目空間運動的幾何模型和導引頭體視線角的測量模型，并將其分別作為系統狀態方程與量測方程，采取擴展卡爾曼濾波、無跡卡爾曼濾波以及其他形式的非線性卡爾曼濾波器估計得到彈目視線角速率[4-6]。該類算法濾波參數的設置通常依據經驗確定，因此算法穩定性及快速性受設計者的經驗影響較大。

文中以搭載捷聯相控陣導引頭的某末制導彈藥為研究對象，利用導引頭體視線角、彈目相對距離、相對速度等信息，建立了彈目相對運動幾何關系及導引頭體視線角測量的數學模型，并將其分別作為濾波系統的狀態方程和量測方程。該系統具有高度非線性的特點，而自適應無跡卡爾曼濾波(AUKF)算法適用于強非線性系統的參數估計，且濾波參數可自適應在線調整，因而AUKF算法具有更好的穩定性與快速性。基于上述分析，利用AUKF算法估計得到了彈目視線角速率，通過彈道閉環仿真試驗驗證了算法的正確性與有效性；同時采用蒙特卡洛模擬打靶試驗，證明了AUKF算法比α-β微分濾波器具有更高的命中精度；最后，為了對算法的實時性進行分析，在某微處理器上初步實現了視線角速率的AUKF估計，結果表明AUKF算法的平均運行周期小于6 ms，可滿足彈載環境的實時性要求。

2 導引頭視線角速率估計數學模型

2.1 坐標系及轉換關系定義

為了便于描述彈體姿態角、彈目視線角及導引頭體視線角之間的幾何關系，定義以下4個坐標系：發射坐標系Oxyz,彈體坐標系Ox1y1z1,視線坐標系Oxsyszs以及體視線坐標系Oxbsybszbs，各坐標系間的相應轉換關系如圖1所示，其轉換方法及角度的具體定義方式見參考文獻[7-8]。

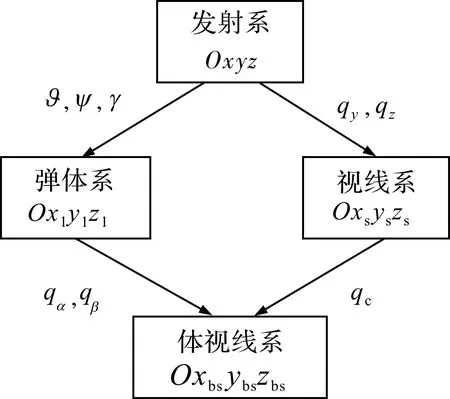
圖1 坐標系間轉換關系

2.2 捷聯相控陣導引頭視線角速率濾波模型

1)彈目相對運動幾何關系建模

末制導彈藥在飛行過程中，彈目視線角及視線角速率受空間幾何關系約束。視線坐標系相對于發射坐標系的旋轉角速度ωs在視線系下的坐標為：

(1)

其中，L(·)表示初等變換矩陣，具體定義方式見文獻[7]。

設r為彈目距離，彈目相對位置矢量rTM在視線坐標系下的坐標為：

(2)

對式(2)求導，可得末制導彈藥與目標的相對速度VTM在視線坐標系下的坐標：

(3)

對式(3)求導，同樣可得到末制導彈藥與目標的相對加速度aTM在視線坐標系下的坐標：

(4)

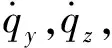
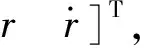
(5)

其中ax,ms,ay,ms,az,ms為彈體加速度在視線坐標系下的分量，可由慣性導航系統提供。

2)導引頭體視線角建模

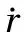
(6)

其中，Rij表示由發射系到彈體坐標系轉換矩陣的相應元素[6]。

由于彈目距離在末制導段快速變化，模型的準確度受式(5)中彈目距離x5、接近速度x6影響較大，因此對導引頭的測距及測速信息加以利用，有利于提高視線角速率的估計精度。

3 AUKF算法

改進的Sage-Susa自適應濾波算法是一種時變噪聲估計器，能夠利用測量器件的量測數據，實時修正濾波系統的過程噪聲及量測噪聲，降低濾波系統誤差、抑制濾波過程發散，進而提高系統參數的估計精度；UKF算法是線性最小方差估計的近似形式，同時適用于線性系統與非線性系統，系統狀態方程與量測方程的非線性度越強，其優勢越明顯[11]。將Sage-Susa自適應濾波算法與UKF算法的優勢結合，形成自適應無跡卡爾曼濾波算法(AUKF)，特別適用于式(5)、式(6)所示的強非線性系統，并能實時估計出由于彈道參數變化造成的過程噪聲與量測噪聲。

假設上述非線性系統狀態方程及量測方程的離散矢量形式為：

(7)

式中：xk,xk-1為k時刻、k-1時刻的系統狀態;wk為由于建模不準確及模型參數誤差引起k時刻的過程噪聲;zk為k時刻的系統量測量;vk為系統k時刻由于導引頭測量誤差引起的量測噪聲。

假設系統的過程噪聲與量測噪聲皆為白噪聲，協方差矩陣分別為Qk,Rk。在無跡卡爾曼濾波的基礎上，AUKF算法還對濾波噪聲的期望及協方差進行如下自適應估計：

(8)

式中，b為衰減因子，通常取0.95～0.99。式(5)～式(8)即為捷聯相控陣導引頭視線角速率的AUKF估計算法。

4 仿真驗證

4.1 數學仿真

某末制導彈藥采用捷聯相控陣雷達導引頭，基于此彈藥的典型彈道，在慣性導航系統、相控陣雷達導引頭測量參數存在零位誤差及白噪聲誤差的條件下，通過數學仿真研究捷聯相控陣導引頭視線角速率的濾波估計技術。

1)參數設置

當目標未進入雷達導引頭的捕獲域前，末制導彈藥利用慣性導航系統提供的彈體位姿信息及裝定的目標位置，按照比例導引的方式接近目標；目標進入導引頭捕獲域后，通過AUKF算法估計彈目視線角速率，并采取比例導引律引導末制導彈藥飛向目標。

算法的啟動參數設置如下：

q0=[0 0 0 0 0 0]T,r0=[0 0 0 0]T,b=0.975,Q0=diag6(1×10-8),R0=diag4(1×10-5),P0=diag6(1×10-8)。

其中diagm(n)表示以n為主對角元的m階對角矩陣。

2)數學仿真結果

α-β微分濾波器是一種二階濾波器，其原理與無輸入量的一維卡爾曼濾波器基本相同[12]。當制導器件具有相同的測量精度，分別采用AUKF算法、α-β微分濾波器估計所得視線角及視線角速率如圖2～圖5所示。

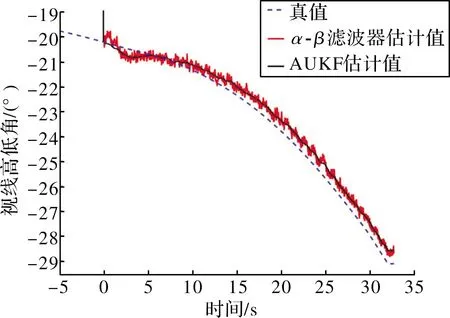
圖2 視線高低角

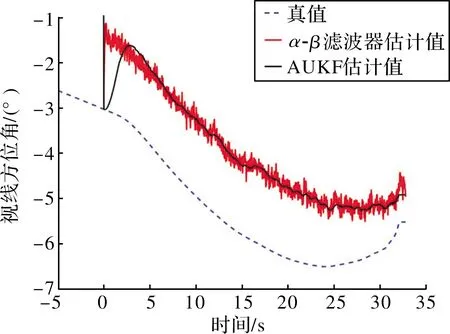
圖3 視線方位角

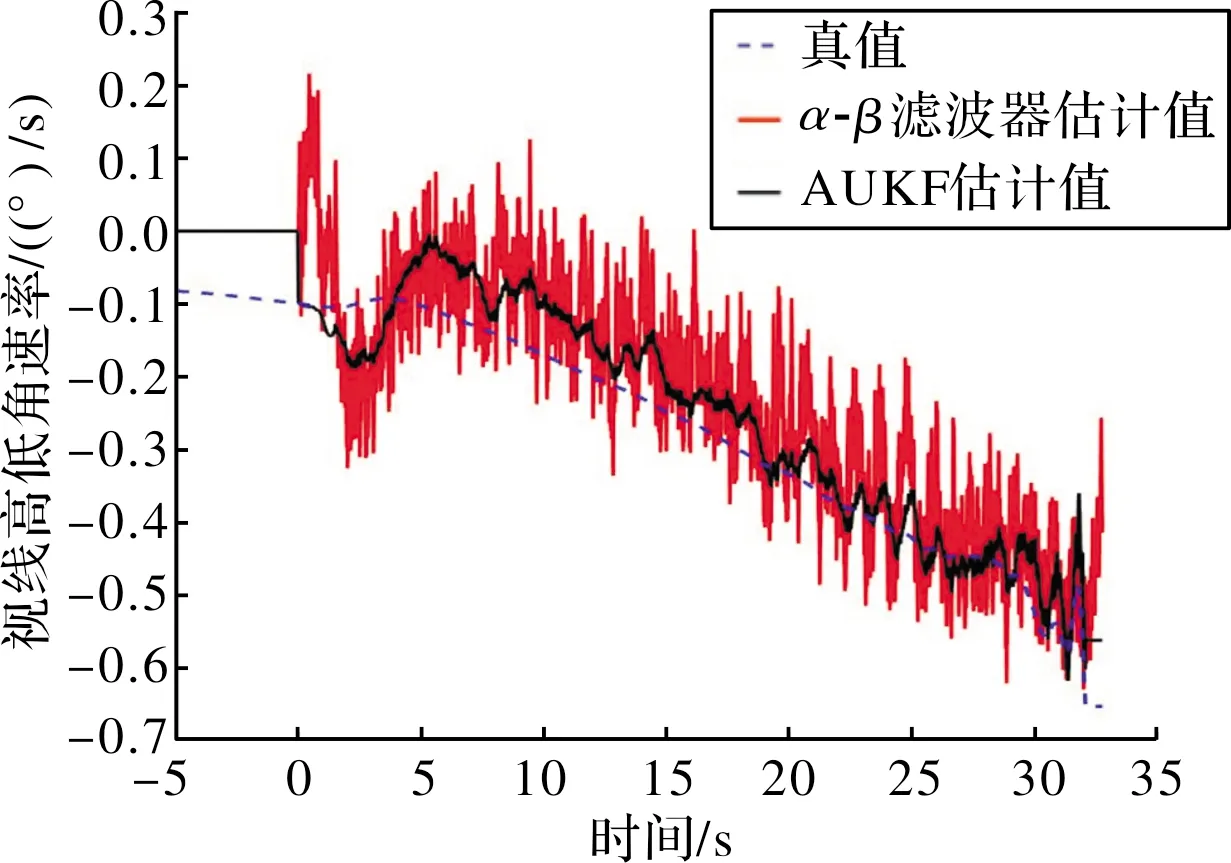
圖4 視線高低角速率

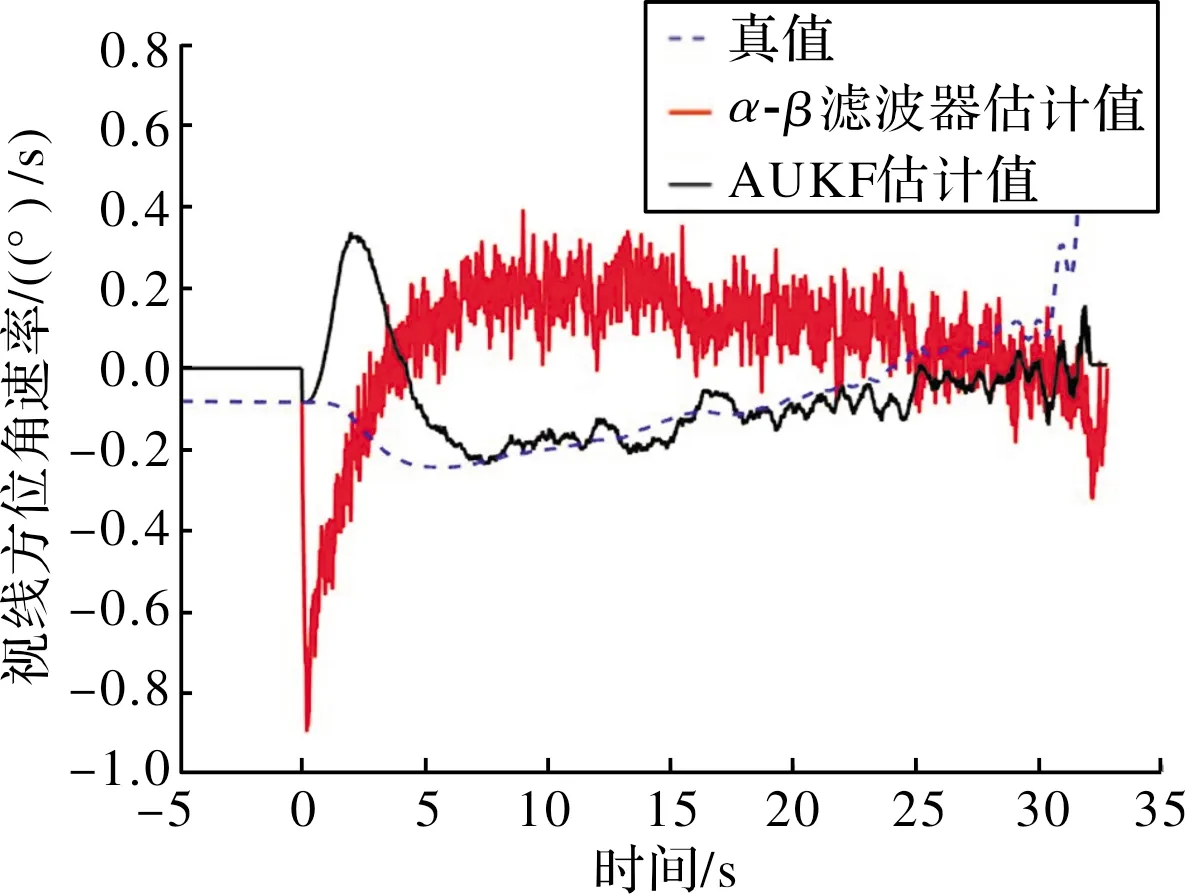
圖5 視線方位角速率

仿真結果表明：目標進入導引頭的捕獲域后，AUKF算法可有效隔離制導器件測量噪聲對制導系統的影響，快速估計出彈目視線角及視線角速率，同時慣性導航系統的零位誤差僅影響了視線角的測量精度，經“微分”后得到的視線角速率不受其零位誤差影響。采用捷聯相控陣導引頭的某末制導彈藥，基于AUKF算法估計彈目視線角速率時，單次仿真脫靶量為1.3 m，具備對敵目標精確打擊的能力；與α-β微分濾波器相比，AUKF算法具有更高的跟蹤速度和估計精度，可減小制導器件測量誤差對視線角速率估計的影響程度，提升制導系統工作性能。

4.2 制導精度分析

采用AUKF算法和α-β微分濾波器，分別進行5 000次蒙特卡洛模擬打靶數值試驗，落點散布如圖6、圖7所示，仿真結果表明，相對于常規的α-β微分濾波器，AUKF算法可有效減小末制導彈藥的脫靶量。

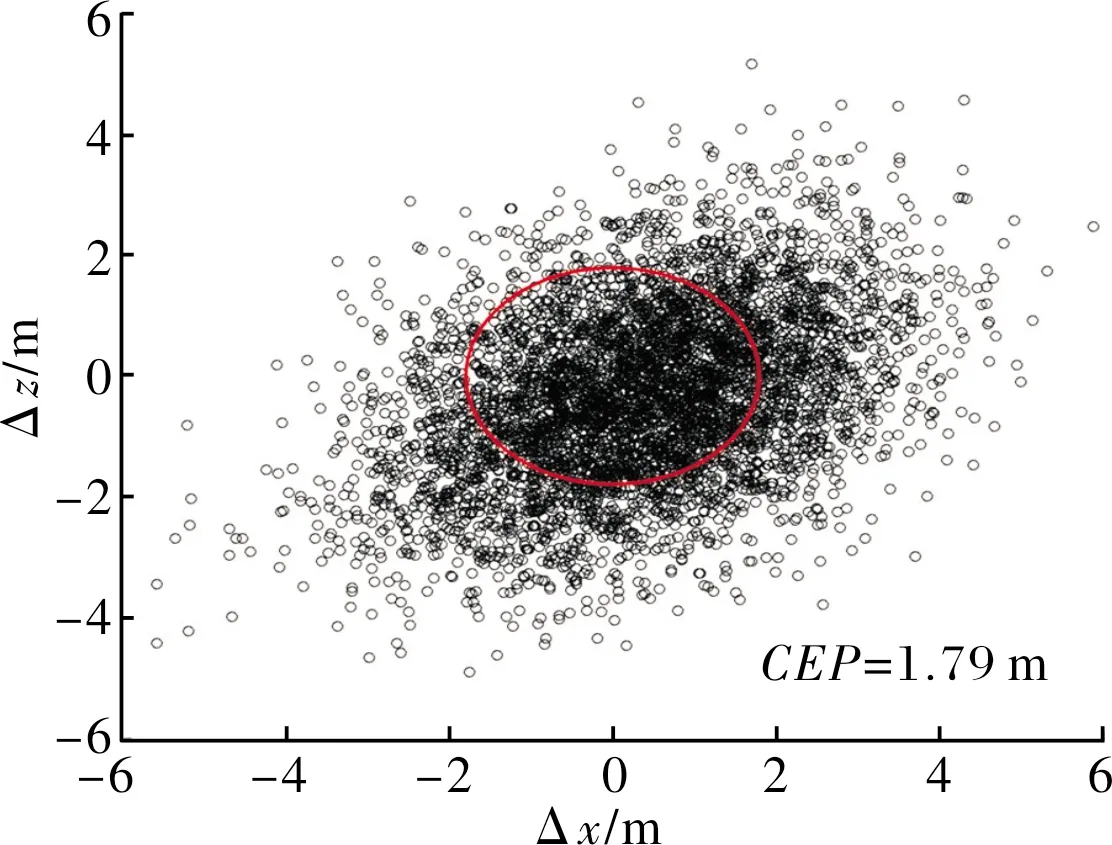
圖6 落點散布(α-β微分濾波器)

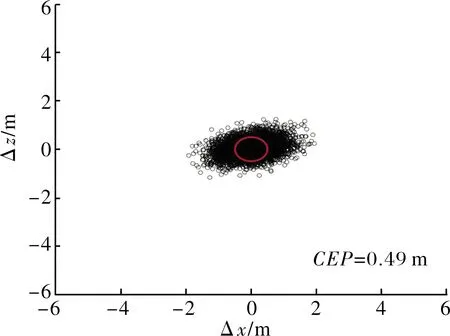
圖7 落點散布(AUKF算法)

4.3 實時性分析

AUKF算法需進行大量的矩陣運算，其核心問題是濾波運算的實時性。實時性一般可通過對算法分解簡化、并行處理等方式保證，但最根本的途徑是提高芯片的數據處理能力。GigaDevice公司生產的基于ARM Cortex-M4內核的某微處理器，工作主頻為200 MHz，該處理器具有體積小、易擴展等特點；文中使用C語言編寫源程序，在該微處理器上實現了視線角速率的AUKF估計，并采用計時器對算法的運行時間進行了估計。

α-β微分濾波器實現一次濾波運算，僅需進行10次浮點數運算(6次乘法、4次加法)，運行周期可忽略，而AUKF算法單次運行的平均周期為5.5 ms(估計誤差為0.5 ms)。由于捷聯相控陣導引頭的數據更新周期為20 ms，因此在上述處理器上實現視線角速率的AUKF估計，可保證實時性要求，并留有充分的時間裕度。

5 結論

以某末制導彈藥為研究對象，充分利用彈目相對距離及相對速度等制導信息，推導了一種適用于捷聯相控陣導引頭的視線角速率估計模型，將其與AUKF算法相結合，提出了基于AUKF算法的捷聯相控陣導引頭視線角速率的估計算法。數學仿真結果表明，在制導器件具有相對較低的測量精度時，所提算法與α-β微分濾波器相比，對彈目視線角速率的估計更為準確，閉環仿真具有更高的命中精度；在實時性方面，AUKF算法比α-β微分濾波器的運算量大，但其濾波周期仍小于導引頭的數據更新周期，因此在微處理器上實現捷聯相控陣導引頭視線角速率的AUKF估計是可行的。

對于捷聯末制導彈藥，除對視線角速率的準確估計外，還應對彈道設計及中末制導交接班等關鍵技術進行研究，保證在目標位置拉偏時中末制導交接段的控制指令能夠平滑過渡；此外，在捷聯制導器件的測量誤差及視線角速率估計噪聲較大的條件下，控制系統還必須具備一定的魯棒性，在飛行過程中才能使彈體姿態保持穩定，以減小脫靶量。