基于神經網絡的變后掠翼飛行器自適應控制方法研究

李墨吟，馬澤遠，周建平，張云飛，夏群利

(北京理工大學宇航學院，北京 100081)

0 引言

變形飛行器作為一種新概念飛行器，在未來民用和軍用領域都有著廣泛的應用前景，其變形方式包含了變展長、變弦長、變厚度、變后掠以及變彎度等。本質上，變形飛行器可以認為是一類涵蓋了多種氣動性能模式的特殊飛行器，不同的氣動性能可適用的作戰場景與任務也不同。例如，遠程打擊作戰場景中，飛行器需要更大的航程，此時，大升阻比的氣動構型能夠為飛行器提供足夠的升力以保證續航飛行能力，而在末段俯沖打擊任務中，更小的阻力，更大的側向過載能力能夠增強飛行器的突防能力。因而，變形飛行器研究逐漸成為學術界和工程界的研究熱點[1-4]。

近年來，隨著現代控制理論的推進，各種新型控制方法應運而生，對于傳統飛行器，張廣勇等[5]在動態逆控制律的基礎上，利用神經網絡進行誤差補償實現了自適應控制。劉曉岑等[6]針對高超飛行器姿態控制問題，在考慮輸入飽和的情況下，設計了具有強魯棒性的基于滑模觀測器的動態面控制方法，該方法能夠保證控制輸入更平滑且尖峰值更小。而對于變形飛行器控制問題，聶博文等[7]研究了一種可折疊變形的飛行器過渡飛行控制策略，針對垂直起降和高速巡航模態狀態銜接問題，通過試驗驗證了該方案的有效性。鄭曼曼[8]利用T-S模糊理論描述整個變體過程，以此設計了T-S模糊飛行控制器。熊英等[9]針對變后掠翼飛行器，研究并設計了非線性多模型切換系統，利用非線性干擾觀測器對復合干擾逼近以實現姿態跟蹤。而人工神經網絡[10-11]作為一類具有逼近任意函數功能的系統，可以實現在復雜環境下的自適應控制。對于變后掠翼飛行器而言，變后掠角過程中氣動參數的改變對于控制系統提出了一定的挑戰，因此有必要研究針對該類飛行器的自適應控制律。

文中研究了變后掠角過程中飛行器姿態穩定控制問題。首先利用氣動仿真軟件Datcom建立了變后掠翼飛行器在不同形變狀態下的氣動模型。然后建立適應變后掠翼飛行器姿態動力學、運動學模型，并利用動態逆理論處理該類飛行器姿態運動模型中的強耦合問題，在此基礎上，將PID參數設置為神經網絡隱藏層的節點，實現PID參數自適應調整。進一步地，研究了存在外界干擾下的變后掠翼飛行器姿態穩定控制問題。最后仿真結果驗證了其有效性。

1 考慮變形參量的飛行器姿態運動模型

在研究變后掠翼飛行器姿態控制問題中做出如下幾點假設：

1)飛行器為剛體，且在變形過程中速度、質量保持不變；

2)地面坐標軸系為慣性坐標系；

3)忽略地球自轉，將地球看作均勻質量圓球。

針對面對稱的變后掠翼飛行器，建立如下考慮變形參量的無動力飛行姿態運動方程組[6]：

(1)

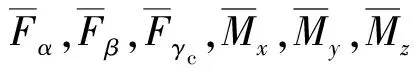
2 變后掠翼飛行器氣動模型建立

變后掠翼飛行器構型如圖1所示，其頭部為圓錐，彈身為圓柱，兩側為面積較大的梯形升力翼，提供飛行過程中大部分的氣動力，控制舵位于彈身尾部，呈“+”型分布，可提供少部分氣動力。

圖1 變后掠翼飛行器示意圖

變后掠翼通過改變后掠角來改變飛行器的氣動性能，在工程中已被一些飛行器采用，因此文中基于該變形方式，利用氣動仿真軟件Datcom，計算不同后掠角狀態下的飛行器氣動特性，以此建立變后掠角飛行器的氣動與變形量之間的函數。

考慮后掠角變化范圍在0°～60°，以30°,60°后掠角的升力系數、俯仰力矩系數為例，其氣動特性如圖2～圖5所示。

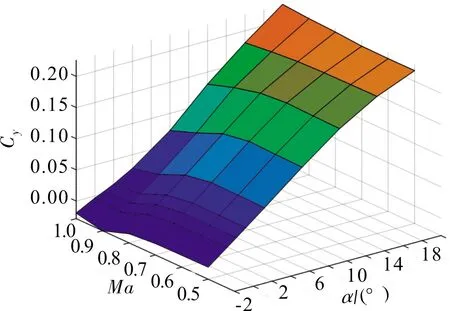
圖2 30°后掠角下的升力系數

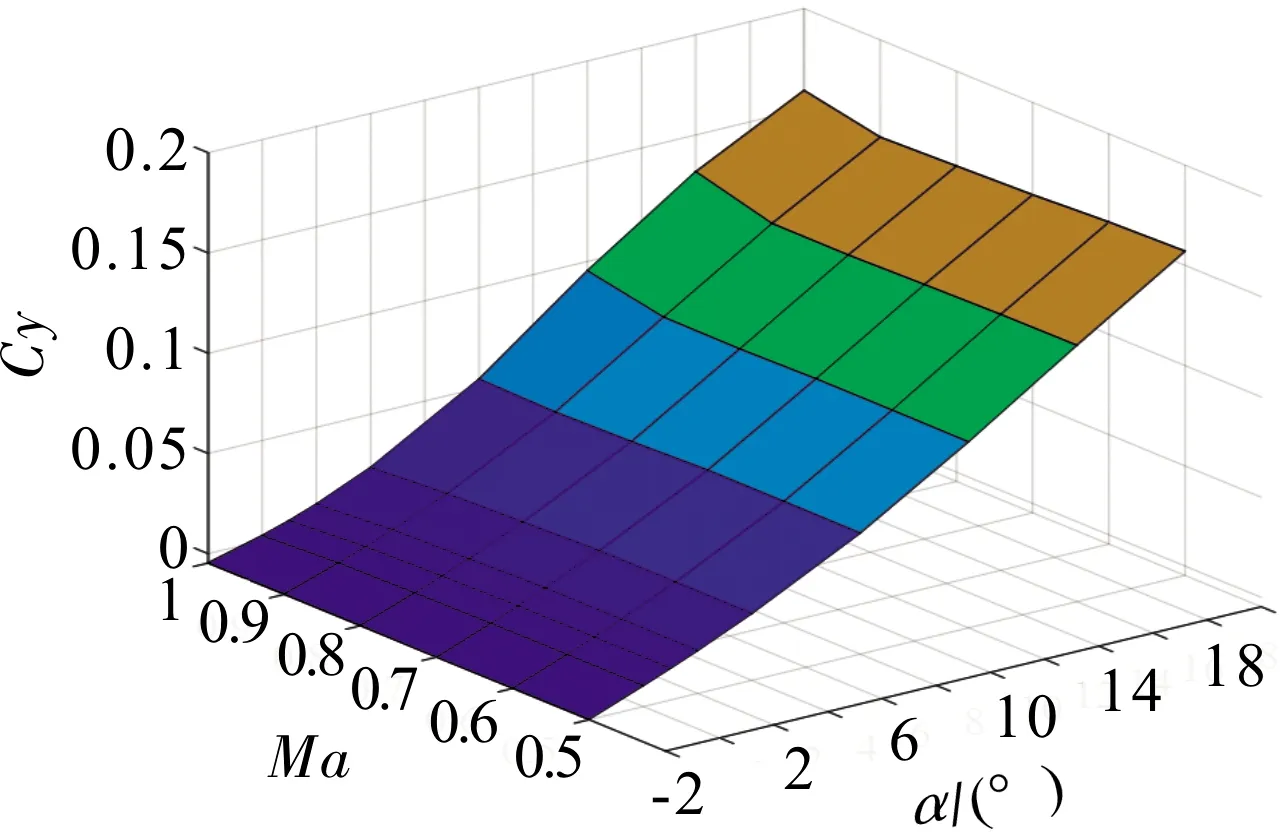
圖3 60°后掠角下的升力系數

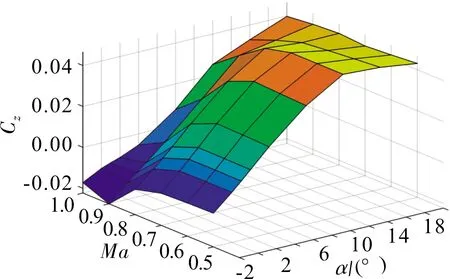
圖4 30°后掠角下的俯仰力矩系數

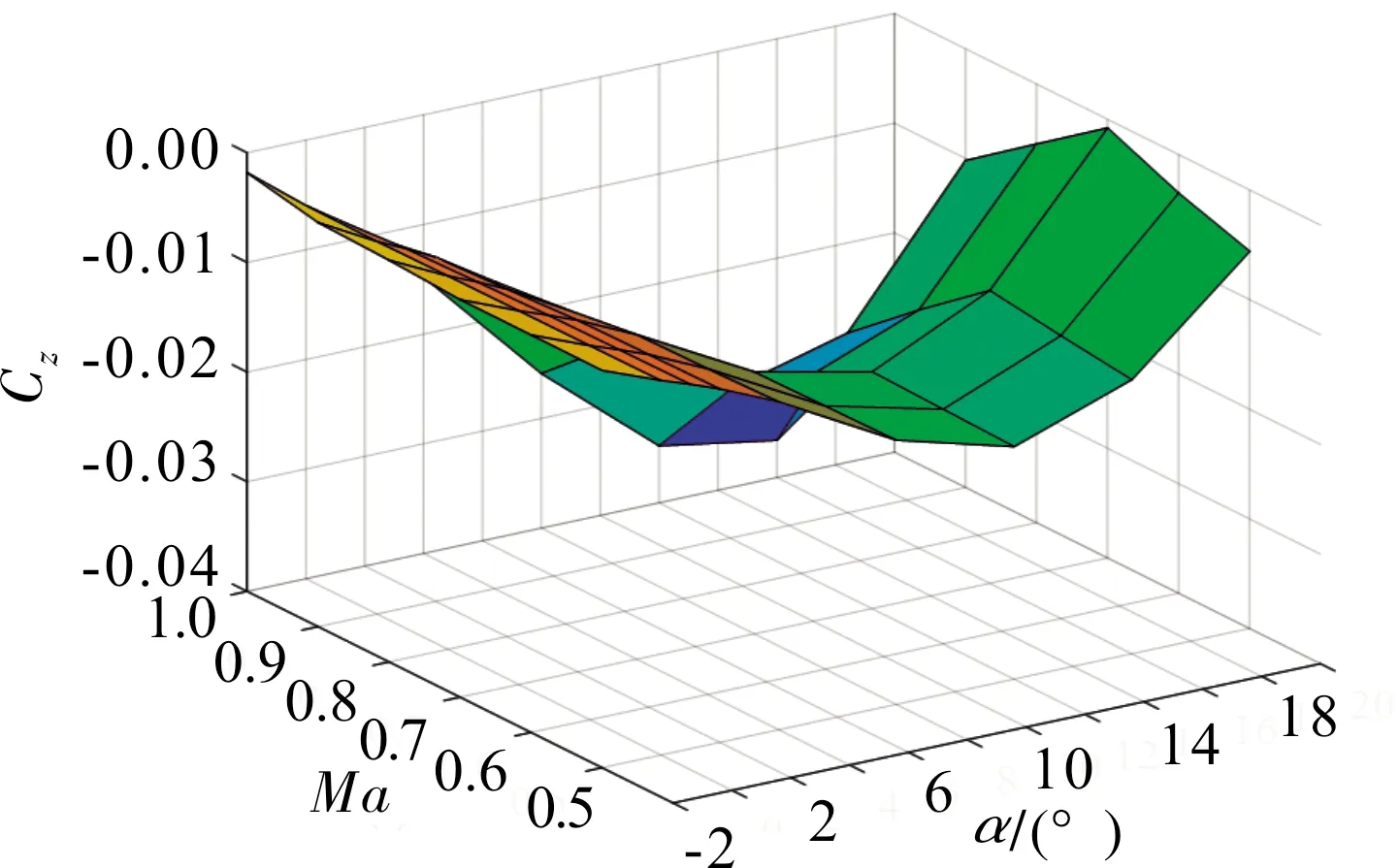
圖5 60°后掠角下的俯仰力矩系數

根據Datcom計算得到的氣動數據，建立包含形變參量的飛行器氣動力和氣動力矩表達式：

(2)

式中：q,S,l為動壓、飛行器參考面積及參考長度；CY(η),CZ(η)為升力系數、側力系數；Cx(η),Cy(η),Cz(η)為滾轉、偏航、俯仰力矩系數。為了更好的實現控制器的設計，可以將氣動系數在特征點處擬合成線性化形式，如式(3)所示：

(3)

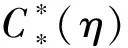
綜上，結合第1節中的飛行器姿態運動方程式(1)，建立了包含不同后掠角的氣動特性變后掠翼飛行器姿態運動學動力學模型。

3 基于神經網絡的PID自適應動態逆控制方法

3.1 動態逆控制結構

由運動方程式(1)可知，系統的狀態變量有α,β,γc,ωx,ωy,ωz共6個，而系統的控制變量只有δx,δy,δz，由于動態逆控制方法需要控制對象滿足控制量與狀態量個數相等，因此根據奇異攝動理論需要對狀態變量進行時標分離。考慮飛行器姿態角變化相對于角速度變化慢，由此將整個飛行器姿態控制系統劃分為慢變子系統和快變子系統。結合式(1)～式(3)建立面向變后掠翼飛行器姿態動態逆控制的狀態方程[6]：

(4)

式中:x1=[αβγc]T，x2=[ωxωyωz]T代表狀態量;u=[δxδyδz]T為控制變量。第一個公式代表慢變量回路，第二個公式代表快變量回路。ξ1,ξ2為飛行器所受到的外界干擾。f1(x1,θ)，g1(x1)，f2(x1,x2)，g2(x2)具體形式如式(5)～式(8)。

(5)

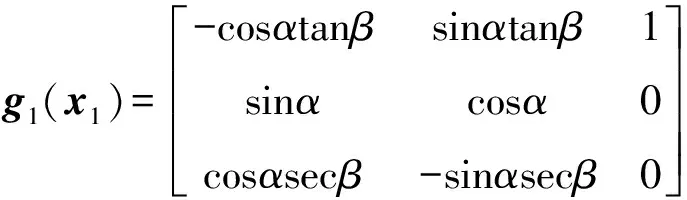
(6)

(7)

(8)

其中，當側滑角β≠±90°時，矩陣g1(x1)可逆。綜上，可得變后掠翼飛行器快慢子系統控制律為：

(9)

3.2 基于神經網絡的PID自適應控制器設計

在實際飛行過程中，PID參數通常是預置好的，而在變形過程中，預置參數不一定完全適應整個飛行過程，因此，提出了一種利用神經網絡對PID參數進行自適應調整的策略，使得控制器能夠在飛行器變形過程中實時調節PID參數。該方法將PID的3個參數設置為神經網絡隱藏層中的基函數，通過不斷計算當前控制參數對被控對象的狀態影響進行迭代訓練，采用梯度下降的策略對輸出層的權重進行調整，神經網絡PID自適應控制器結構如圖6所示。

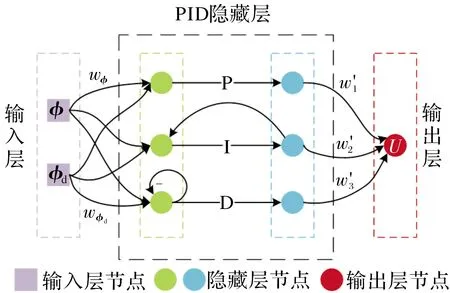
圖6 神經網絡PID控制結構

該網絡結構的輸入包含狀態量的期望值φd與狀態量的實際值φ，即：

(10)

(11)

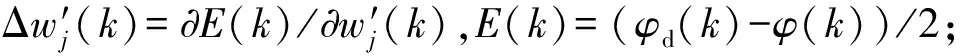
結合式(11)，給出基于神經網絡的PID自適應控制律為：

(12)

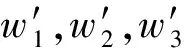
(13)

對于該控制律，為保證系統穩定，需要ΔE<0，根據式(13)可得：

(14)

綜上，建立的針對變后掠翼飛行器控制系統流程如圖7所示。

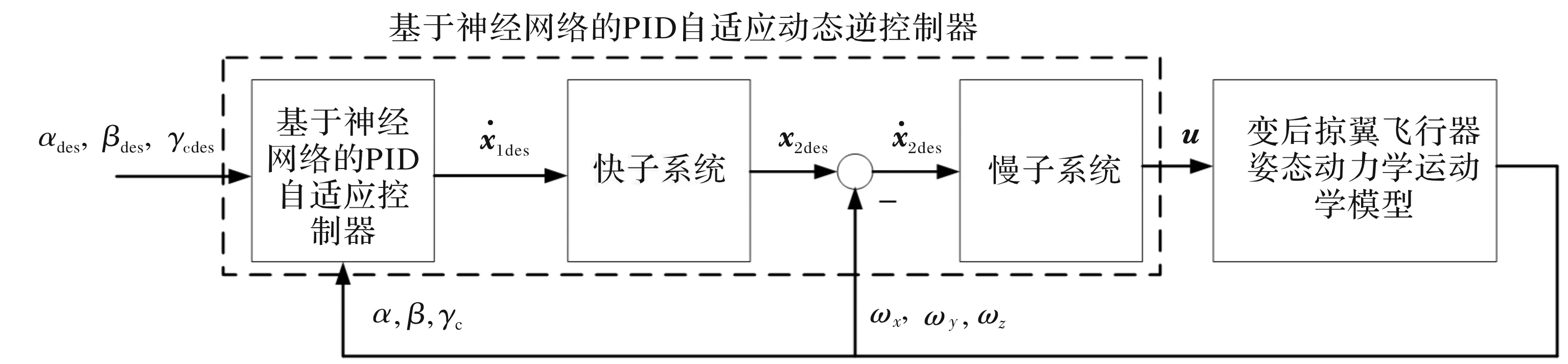
圖7 變后掠飛行器控制系統流程圖

4 仿真分析

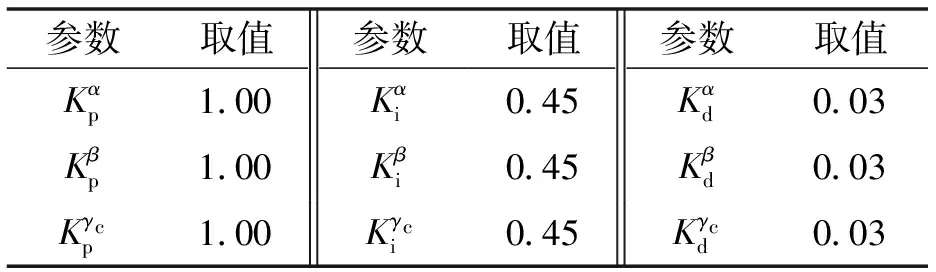
表1 控制器初始參數設置

圖8～圖10展示了基于神經網絡動態逆PID自適應控制律的跟蹤效果，對比可以看出：文中提出的控制律在響應速度、超調等方面均優于傳統的動態逆PID控制律，姿態跟蹤的超調相比傳統控制律下降了33.03%～40.52%，干擾產生的擾動下降了42.33%～75%。從圖11～圖13可以看出：由于動態逆控制方法將變后掠飛行器在變形過程中的氣動參數引入到了控制量中，在t=[1 s,2 s]的變后掠角過程中，該控制律能夠有效穩定住飛行器的姿態;當t=3 s時，飛行器在外部干擾下，自適應控制律能夠在充分利用舵機資源的情況下迅速的穩定飛行器姿態，因此，該方案具有更合理的輸入控制設計，能有效調度控制資源，提升系統的控制性能。

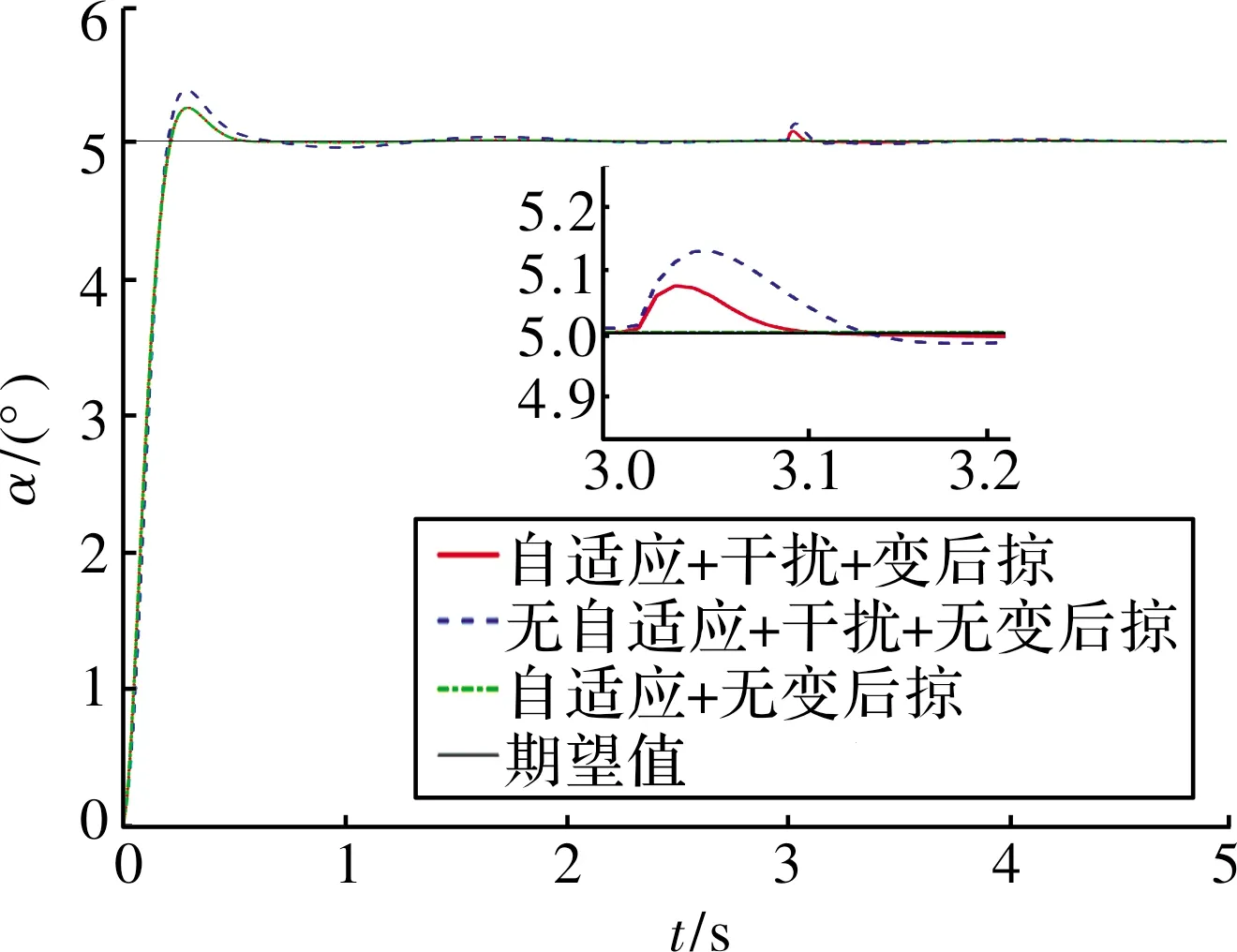
圖8 攻角曲線

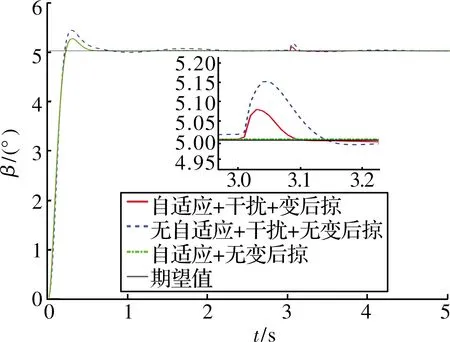
圖9 側滑角曲線

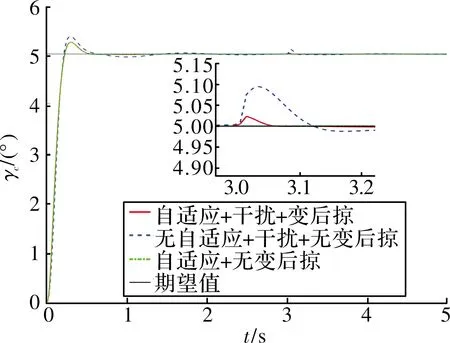
圖10 傾側角曲線

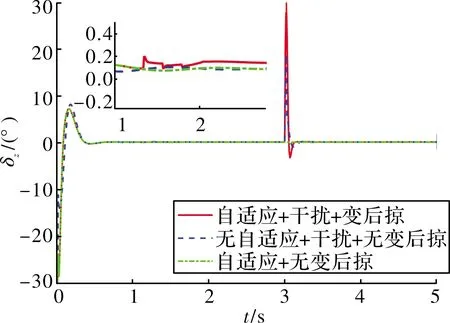
圖11 副翼曲線

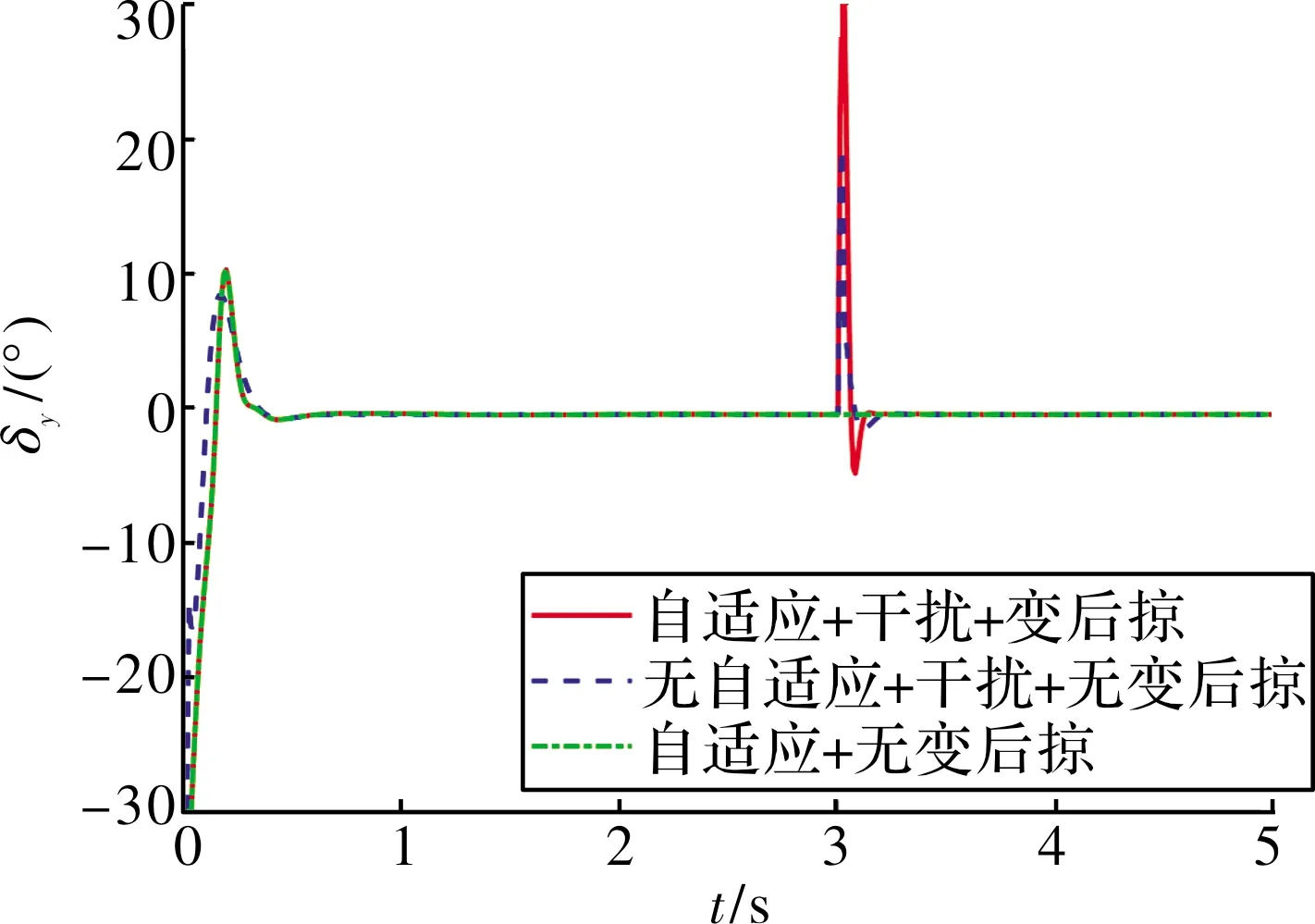
圖12 方向舵曲線

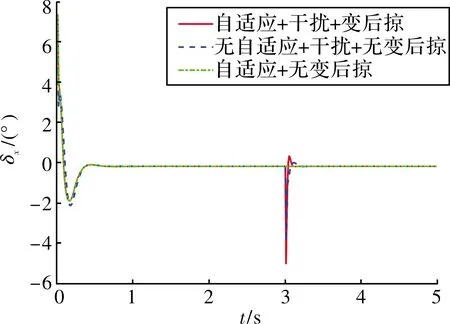
圖13 升降舵曲線

5 結論

將PID參數作為神經網絡隱藏層，利用梯度下降策略有效實現了變后掠翼飛行器在變形、受干擾情況下的參數自適應控制。采用基于神經網絡的PID自適應動態逆控制方法，在響應時間、超調、對干擾的抑制程度以及舵資源的利用率上對于傳統控制形式均有所提高。但該方法仍依賴于動態逆控制律，因此對于飛行器的精確建模具有較強的依賴性，后續會針對弱模型依賴的自適應動態逆控制問題開展研究。