極端條件下大長徑比固體發動機藥柱結構完整性快速分析

余 瑞，張 路，何 君，吳 敏，唐承志，鄧康清，郭 翔，龐愛民

(1 航天化學動力技術重點實驗室，湖北襄陽 441003；2 湖北航天化學技術研究所，湖北襄陽 441003)

0 引言

固體火箭發動機在制造、勤務、發射和飛行的過程中，會受到固化降溫、點火增壓、沖擊振動和飛行過載等載荷的作用，可能導致發動機藥柱產生過大的應力和應變，造成發動機故障，因此有必要開展各種單一載荷或者組合載荷條件下的藥柱結構完整性分析。隨著軍事需求和武器裝備多樣化發展，大部分戰術導彈要求能在低溫下工作，點火增壓和低溫環境的疊加作用使得藥柱結構的完整性問題更加突出[1-4]。

除了外部載荷的作用因素，藥柱結構完整性還和藥形、長徑比、馬赫數及約束等內部結構特征相關。研究表明增加藥形復雜度，增大長徑比、馬赫數，增強約束都會使得藥柱的受力狀況變差，對藥柱的結構完整性不利[2-5]。在有些情況下，為了提高發動機的工作效能，通常采用復雜裝藥設計，例如大長徑比、高馬赫數、星形內孔或翼柱形串聯裝藥等方式，進而達到各種技術、戰術指標要求。這些藥形結構復雜，尺寸不一，應力集中明顯，結構危險點的位置也隨整體藥柱結構變化[5]，再加上外部組合載荷的疊加作用，對發動機的結構完整性提出了嚴峻的挑戰。

針對固體推進劑藥柱的粘彈性特性分析，國內外學者提出了多種粘彈性本構模型來反映藥柱的真實力學響應[6-7]。Ho等認為在瞬態沖擊條件下藥柱產生的應變和應力線性相關[8]，提出的線粘彈性本構模型可宏觀反映粘彈材料的力學特性。多名學者應用線粘彈性本構模型研究了推進劑材料參數[9-11]、藥柱幾何參數[12-13]、侵蝕效應[14]對點火增壓瞬態藥柱結構力學響應的影響。雖然基于線粘彈性本構模型的仿真分析方法可以得到不同時刻藥柱內部的結構力學響應，但不能直觀得到任意時刻藥柱等效模量的變化情況，且計算時間較長[15]。

文中針對某型大長徑比復雜裝藥結構開展了藥柱結構完整性分析，得到了極限溫度條件下點火增壓過程藥柱結構的應力-應變響應，為結構完整性評估提供理論指導。為進一步提高計算效率，對點火增壓下藥柱結構完整性的快速評估方法進行二次開發，編寫了點火增壓藥柱結構完整性快速評估程序，并應用該程序分析得到關鍵位置極端溫度點火增壓過程中固體火箭發動機的結構響應，將分析結果與基于線粘彈性本構模型的有限元仿真分析結果進行對比，驗證了該快速評估程序的準確性，為極端溫度點火增壓過程中實際固體發動機藥柱結構完整性的快速分析提供參考。

1 理論模型和計算方法

1.1 線粘彈性本構模型

一般情況下，積分型線粘彈性本構模型適用于線性粘彈性材料的有限元數值計算，在較小應變情況下可用來表征固體推進劑的力學性能[16]，積分型線粘彈性本構模型的三維形式為：

(1)

式中：eij為應變偏張量的對應原素；εkk為應變球向量的對應原素；δij為克羅內克符號(若i=j,則δij=1;否則為0)；ξ,ξ′為等效時間，其定義為：

(2)

式中，αT為溫度-時間轉換因子。剪切松弛模量G(t)、體積松弛模量K(t)可表示為：

(3)

式中:υ為泊松比；E(t)為松弛模量。

1.2 點火增壓過程中藥柱結構完整性快速評估方法

對于確定的固體發動機以及推進劑，藥柱受到階躍內壓力作用時的等效應變僅與壓力和松弛模量有關[17]。藥柱受到階躍內壓力作用時的等效應變可表示為[15]:

ε(t)/Pi=Sp1/E(t)+Sp2

(4)

式中，Sp1,Sp2為藥柱的壓力應變系數。對于簡單圓管形裝藥發動機藥柱，可得到Sp1,Sp2的解析解[17]。對于復雜的發動機，無法得到Sp1,Sp2的解析解，但通過有限元軟件計算得到藥柱在不同恒定壓力載荷下的應變大小，通過擬合可得到壓力應變系數。

設點火增壓過程中，溫度為T，增壓載荷為P(t)=P0(1-eλt)，將增壓時間t劃分成n份，在誤差允許范圍內，分段的壓力階躍函數可代替真實的增壓函數。由式(4)知，每階躍增加壓力ΔPi，產生的應變Δεi和應力Δσi為[15]：

Δεi=ΔPi(Sp1/E(tn-ti-1,T)+Sp2)

(5)

Δσi=E(tn-ti-1,T)Δεi

(6)

設推進劑在參考溫度Ts時的松弛模量為E(t，Ts)，實驗得到推進劑在參考溫度Ts時的WLF(Williams-Landel-Ferry)方程為：

(7)

式中，C1,C2為常數。

T溫度下t時刻的等效模量和時間為：

E(t,T)=E(ξ,Ts)

(8)

(9)

t時刻藥柱總應變ε(t)和總應力σ(t)的表達式為：

(10)

(11)

t時刻藥柱的等效模量可表示為：

Eeq(t)=σ(t)/ε(t)

(12)

2 發動機性能參數

2.1 發動機有限元模型

以某翼柱形裝藥固體火箭發動機為研究對象，結構由殼體、絕熱層、前后人工脫粘層和藥柱組成，燃燒形式為內孔燃燒，其中圓管段藥柱的長徑比約為16.6，馬赫數約為3.7，星形段含有8個星角，肉厚e1=6 mm，根據藥柱結構的對稱性，對發動機的1/16進行仿真分析，共生成242 411個節點，52 706個單元，三維模型如圖1所示。

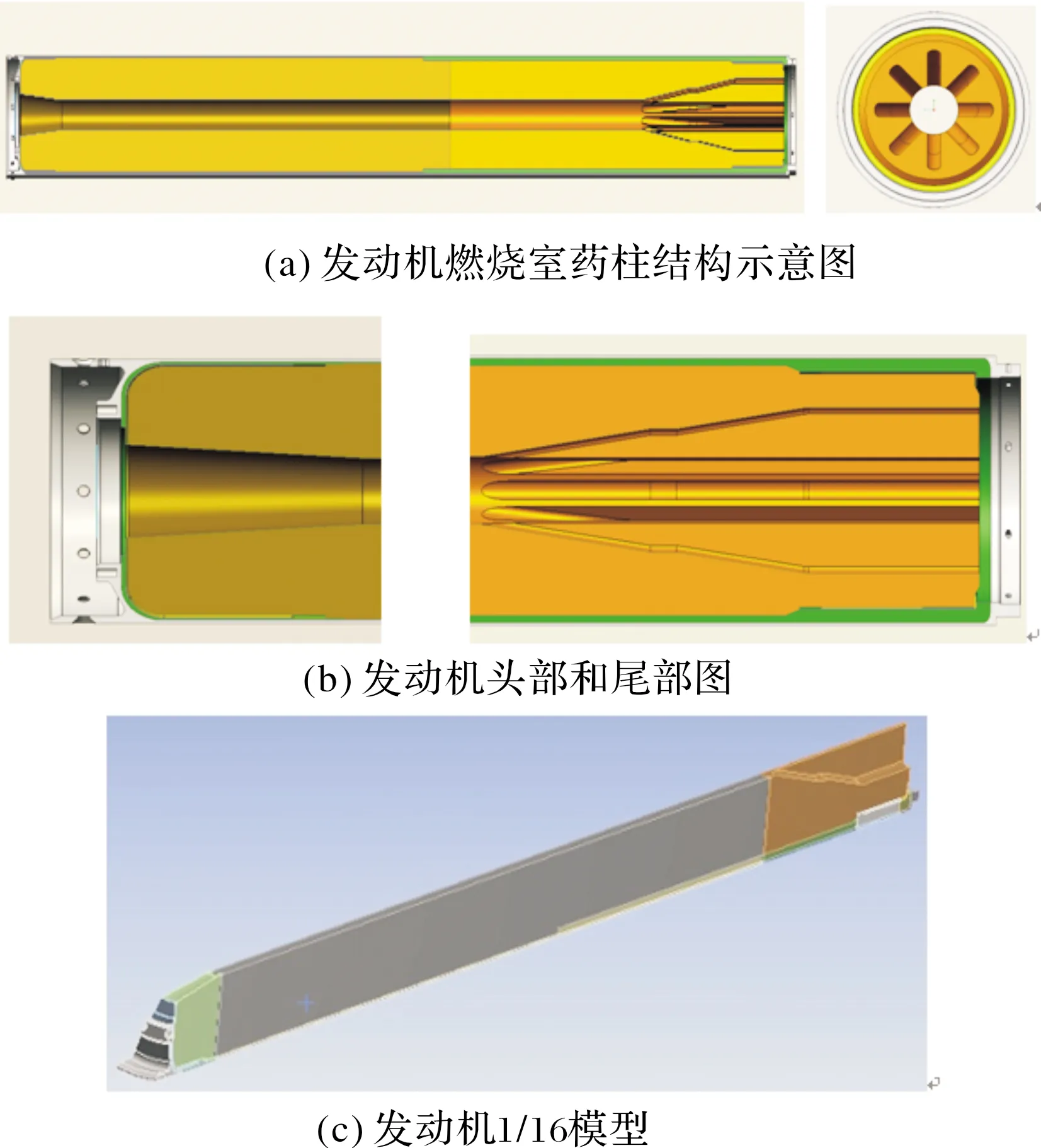
圖1 發動機三維模型示意圖

2.2 載荷及邊界條件

1)載荷工況

固體火箭發動機分別在高溫(60 ℃)和低溫(-40 ℃)下進行點火試驗，點火增壓過程中，燃燒室內部壓力經過約0.1 ms達到峰值8 MPa，假設增壓過程中藥柱受壓均勻，內壓載荷表示為：

P(t)=8(1-e-60t)

(13)

式中：P為內壓；t為時間。

2)邊界條件

依據實際發動機的設計情況，認為殼體與絕熱層、絕熱層與藥柱接觸界面之間粘接牢固。前、后人工脫粘層及內孔表面為自由表面。內壓載荷作用在發動機內部自由表面，同時在對稱面上施加相應的對稱約束，對發動機殼體頭部施加位移約束。

由于增壓時間極短，燃燒室的溫度還來不及傳導至推進劑中，因此假設點火增壓過程中藥柱溫度不發生變化。

2.3 力學性能參數

固體發動機各部件的基本力學性能參數如表1。

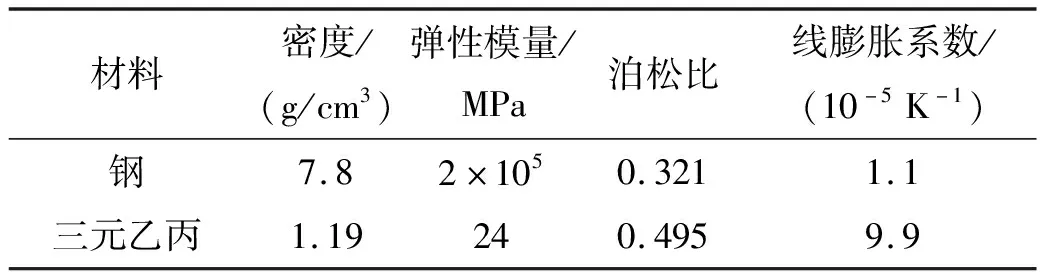
表1 發動機材料基本力學參數

固體發動機藥柱為丁羥體系配方，泊松比為0.495，線膨脹系數為9.9×10-5K-1，對該配方推進劑在各種溫度下的松弛模量進行擬合，得到推進劑相對模量和松弛時間如表2。

表2 推進劑相對模量和松弛時間[18]

已知，固體推進劑的零應力溫度為60 ℃，通過實驗得到推進劑在參考溫度Ts=273.15 K時C1=13.97，C2=253.7。

為確定在壓力載荷作用下發動機藥柱的受力危險部位，選取恒定壓力載荷，得到了藥柱的應力應變分布。計算結果顯示藥柱的危險位置集中在后翼槽頂部位置，藥柱最大等效應力、應變位置如圖2所示。

圖2 藥柱最大等效應力、應變位置

在確定危險位置后，由式(4)可知，計算兩種不同壓力載荷和藥柱模量條件下的等效應變，即可求得危險位置的壓力應變系數。這里選取恒定壓力為8 MPa，藥柱彈性模量分別為5 MPa和10 MPa，對固體發動機進行線粘彈性仿真分析，得到該位置的等效應變分別為0.408 66和0.222 93。將以上數據代入式(4)得到藥柱的壓力應變系數Sp1,Sp2，從而壓力應變方程為：

εeq(t)/Pi=0.2322/E(t)+0.004650

(14)

3 藥柱結構完整性快速評估程序

針對點火增壓過程中藥柱結構完整性快速評估問題進行程序開發，程序流程如圖3所示。通過輸入藥柱材料參數、載荷以及擬合得到的藥柱壓力應變系數可實現藥柱結構完整性的分析。應用該評估界面可快速得到點火增壓過程中藥柱內關鍵位置的等效時間、等效模量、等效應力和等效應變的變化情況。

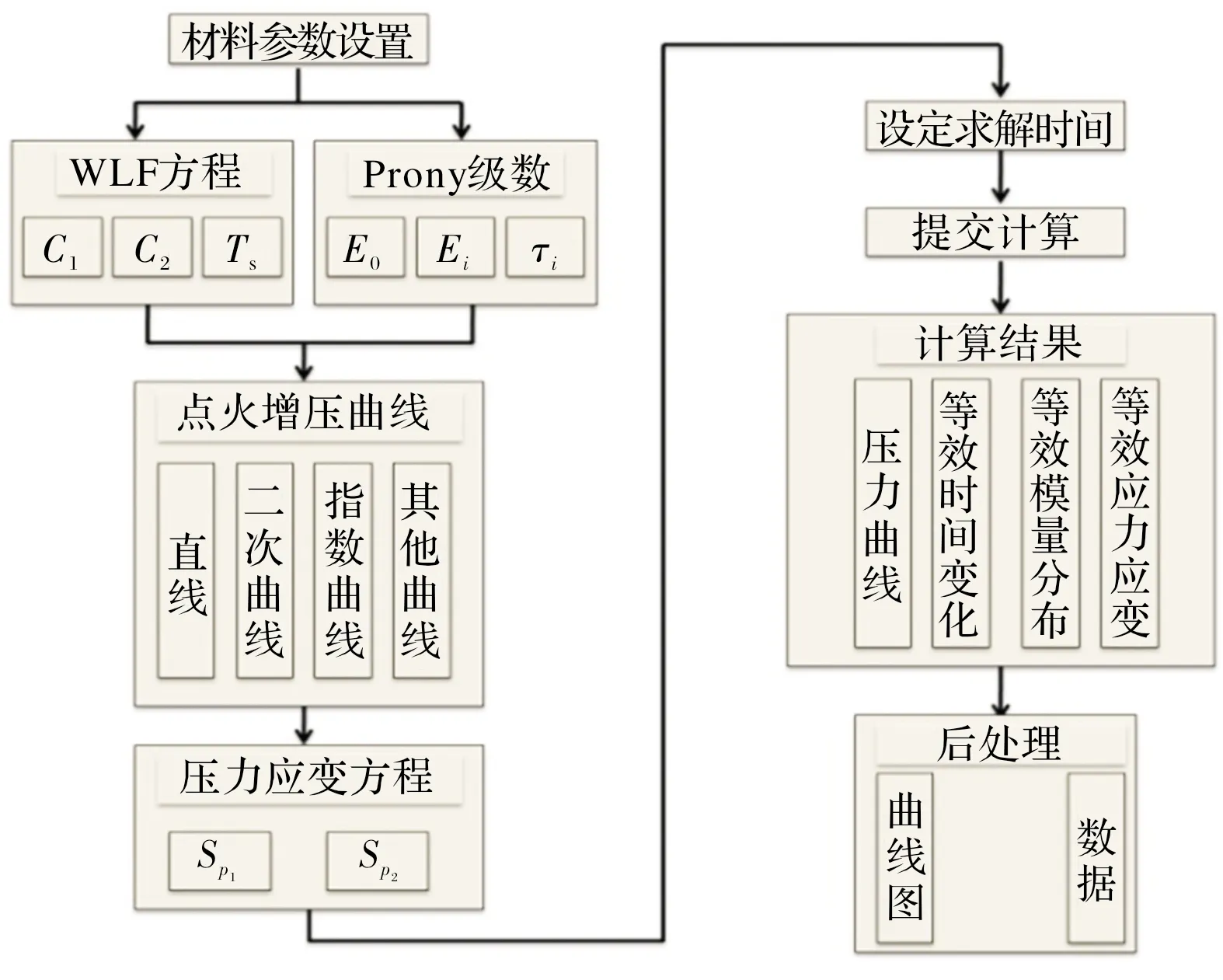
圖3 點火增壓過程藥柱結構完整性快速評估流程圖

4 計算結果與分析

為了分析增壓載荷對藥柱結構完整性的影響，點火增壓過程中不考慮環境溫度變化，分析時認為固體發動機的整體溫度分布均勻且和環境溫度一致。首先，應用ANSYS Workbench基于線粘彈性本構模型對藥柱進行分析，得到藥柱的結構響應；然后，應用點火增壓過程藥柱結構完整性快速評估程序，計算得到極端溫度(60 ℃、-40 ℃)下藥柱內危險位置的等效應變、等效應力和等效模量；最后，將兩種計算結果進行對比分析。

4.1 高溫點火增壓過程中藥柱結構完整性分析

藥柱和環境溫度均為60 ℃,仿真分析得到藥柱內部應力應變分布，藥柱在0.1 s時的等效應變、等效應力分布場如圖4所示。有限元計算和開發的評估程序分析得到的藥柱等效應變、等效應力和等效模量隨時間變化情況分別如圖5、圖6所示。

圖4 60 ℃點火增壓至0.1 s時藥柱等效應變應力場

圖5 60 ℃點火增壓過程中藥柱危險位置應變應力曲線

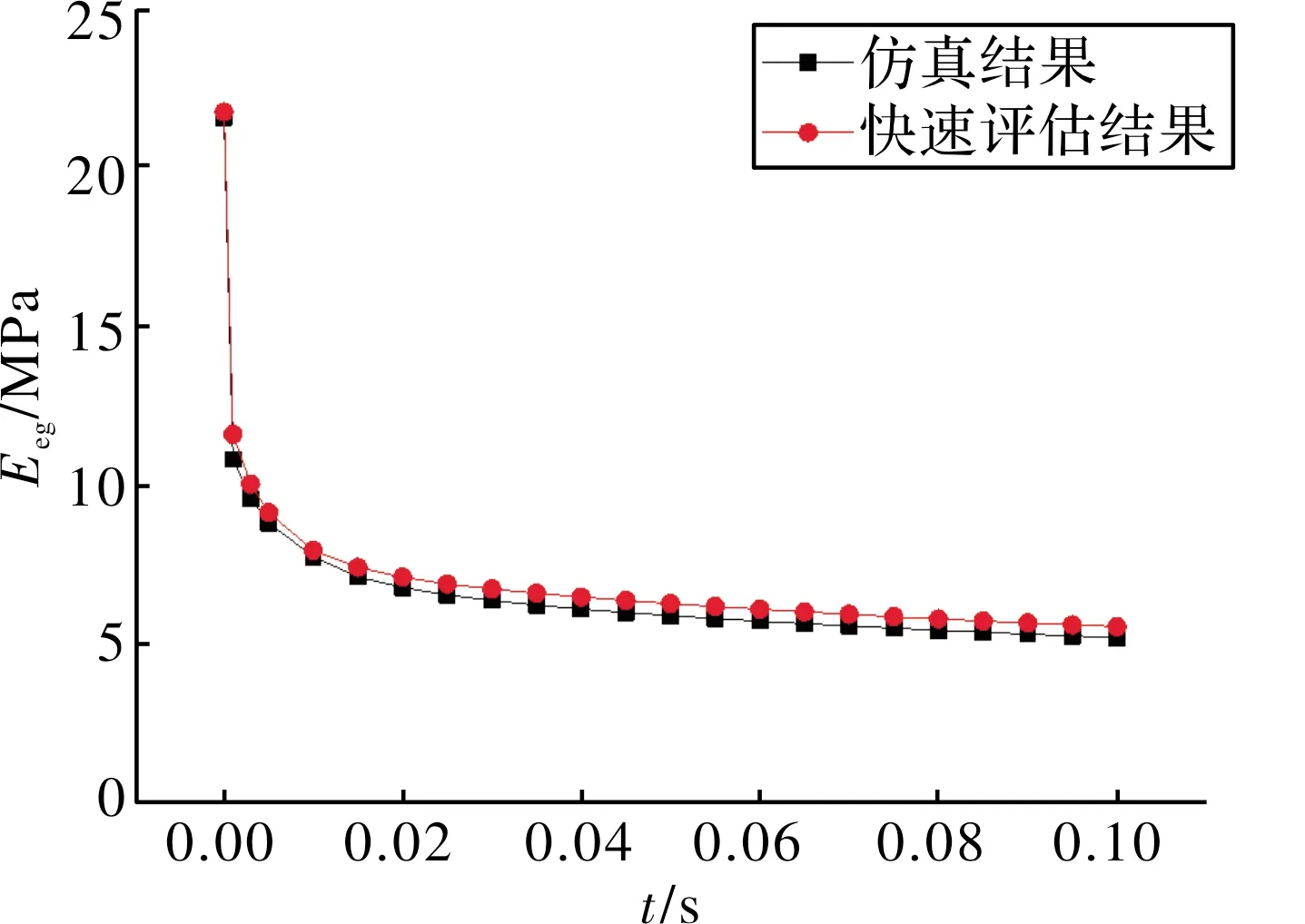
圖6 60 ℃點火增壓過程中藥柱等效模量曲線

由圖4～圖6可知，高溫(60 ℃)點火增壓過程中：1)藥柱的危險位置主要集中在圓管段內表面和翼柱交接過渡處，最大等效應力、應變發生在翼形和圓柱段交界處；2)藥柱的等效應力應變隨著內壓力載荷的增加而增加，在壓力達到峰值時最大，藥柱的等效模量隨著增壓時間逐漸松弛；3)有限元計算和開發的評估程序分析得到的藥柱危險位置等效應變、等效應力和等效模量曲線基本重合。

4.2 低溫點火增壓過程中藥柱結構完整性分析

藥柱和環境溫度均為-40 ℃，低溫點火增壓過程中仿真分析得到藥柱在0.1 s時的等效應變、等效應力分布場如圖7所示，仿真計算和快速評估得到的藥柱危險位置等效應變、等效應力和等效模量的變化情況分別繪制在圖8、圖9中。

圖7 -40 ℃點火增壓時藥柱內部等效應力應變場

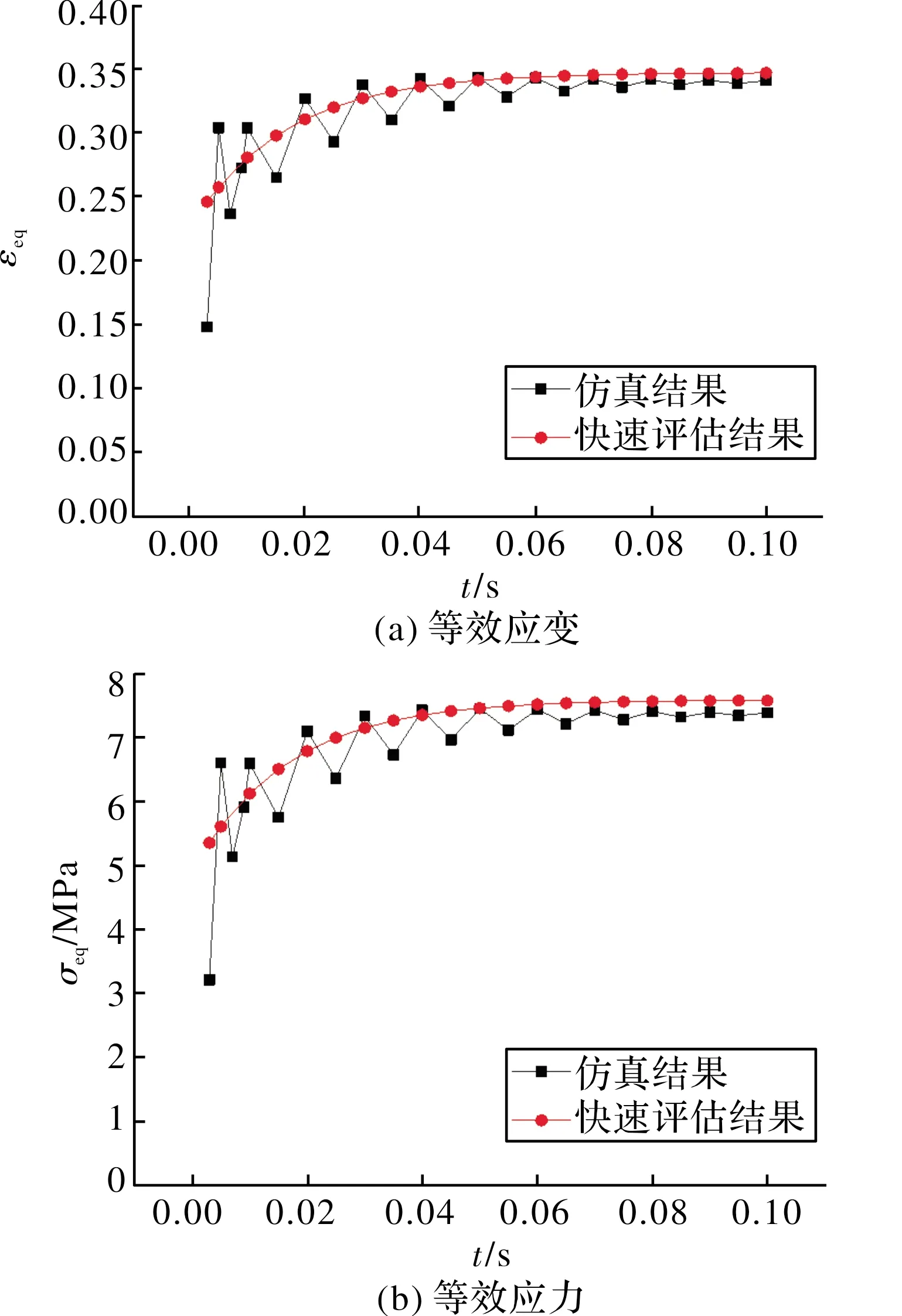
圖8 -40 ℃點火增壓過程快速評估界面

圖9 -40 ℃點火增壓過程中藥柱等效模量曲線

由圖7～圖9可知，低溫(-40 ℃)點火增壓過程中得到的藥柱危險位置與高溫(60 ℃)情況下得到的結果一致。同時仿真計算和快速評估得到的結果變化趨勢一致，誤差較小。

4.3 計算結果統計與分析

由以上計算結果可知，高溫(60 ℃)和低溫(-40 ℃)下點火增壓過程中兩種計算方法得到的危險位置等效應變、等效應力和等效模量最大值發生在0.1 s，因此分別采用快速評估程序和有限元分析兩種方法計算了0.1 s時刻危險位置的力學響應，對比結果見表3。其中需要說明的是，快速評估的計算時間包含壓力應變系數確定前的仿真分析、擬合時間和系數確定后評估程序運行時間。

由表3可知，兩種方法計算結果比較吻合，誤差在4%以內。其中高溫最大等效應變為0.382，低溫最大應變為0.341, 均小于藥柱的極限應變，能夠滿足結構完整性的要求。同時采用快速評估程序計算時間明顯減少，大大提高了計算效率。結果證明該快速評估程序可實現對極端條件下大長徑比復雜固體發動機藥柱結構完整性的快速分析。

表3 計算結果統計與分析對照表

5 結論

1)針對大長徑比翼柱形裝藥結構開展了藥柱結構完整性分析，得到了極限高低溫條件下點火增壓過程藥柱應力-應變的分布規律。結果表明藥柱內孔和翼柱交界面是應力集中區域，最大位置位于翼形和圓柱段交界處。并通過計算得到了危險位置的力學響應，為藥柱結構完整性分析提供理論指導。

2)建立了極端溫度下點火增壓過程固體發動機藥柱危險位置結構完整性的快速評估方法，得到了等效應力、應變、模量和壓力應變系數的具體函數表達形式，并利用C#語言二次開發了極端溫度下點火增壓過程中藥柱結構完整性快速評估程序。

3)應用該程序對極端條件下某翼柱形固體發動機藥柱的結構完整性進行分析，分析結果與基于粘彈性本構模型的有限元仿真結果吻合很好，且基于該程序的計算所需時間大大減少，驗證了快速評估程序的適用性。