促進思維發展的數學課堂提問策略

林麗琴

（仙游縣蜚山第二小學，福建 仙游 351200）

在小學課堂中，提問是一種重要的教學方法。面對問題，學生仔細思考、尋找資料、分析歸納、總結（回答問題），將相關內容納入自身的知識體系。學生解決問題的過程，其實是一個思維發展的過程。通過啟發式、遞進式、開放式三種提問方式，促進學生思維活動從低級走向高級，最終實現學生在小學階段從直觀行動思維到經驗型抽象思維的轉變。［1］

一、啟發式提問：深鉆教材，抓準時機，引導認識事物本質特征

《義務教育數學課程標準（2011 年版）》明確要求：教師在教學的過程中，要懂得靈活使用教材。教師備課時，需充分利用教材編排特點，理解教材中每個模塊和每個探究性結構之間的橫縱聯系，理清思路，劃分重難點，真正吃透教材。在學生實踐探索新知的過程中，抓準時機，采用啟發式提問，具有針對性和有效性，有助于落實學生的主體地位和發揮教師的主導作用，逐步引導學生從具體形象思維向抽象型轉變，以便更好地系統掌握所學的知識。［2］

例如，以人教版六年級上冊《圓的認識》一課片段教學為例，通過對教材的解讀和根據本班的實際情況，設計以下探索圓的特征的教學環節：動手實踐—交流探究—歸納特征—再次畫圓。

師：請同學們用圓規嘗試畫圓。邊畫邊想，畫圓時要注意哪些問題？

（師巡視指導）

師：大部分的同學都畫好了，誰愿意告訴大家用圓規畫圓時應注意什么？

生1：尖尖的那只腳不能動。（圓規要固定）

師追問：動了會怎樣？（圓就跑了，畫不了）

生2：兩條腿的距離不能改變？

師追問：為什么？（也畫不成圓）

師：同樣用圓規畫，為什么有的同學畫的圓大，有的畫的圓小呢？（師舉著兩個大小不同的圓）

生3：圓規兩只腳的距離不一樣。

師追問：圓規兩只腳的距離不同，也就是什么不一樣？（半徑不同）

在師生問答的互動環節中，把握學生的學習狀態，動手實踐，交流歸納，培養學生善于思辨的習慣，學會概括整理。逐步從形成事物的表象到認識事物內在的本質特征，即從具體形象思維過渡到經驗型抽象思維的發展，讓學生感受到知識的魅力和應用知識的樂趣，從“要我學習”轉變為“我要學習”。

二、遞進式提問：分析學情，預設梯度，鏈接新舊知識體系

課前，教師了解學生對知識的真實掌握情況，是實現課堂有效提問的關鍵。只有充分了解學生的實際情況，因利是導、有的放矢、對癥下藥，所預設的問題才有明確的目的和針對性。教師合理預設難度各異的問題，有針對性地讓不同層次的學生都能有所進步，真正做到以學促教。

例如，人教版三年級下冊《小數的初步認識》備課片斷：

磨課一：

師：首先出場的是青蛙，青蛙使勁一跳，誰能說說小青蛙跳了多遠？

……

磨課二：

視頻出示青蛙跳遠的畫面。

案例中，由于第一次備課時沒有深入解讀教材，預設的問題不嚴謹，學生的回答五花八門，有1 分米、10 厘米、一格、一段等答案，不利于學生嚴謹的邏輯思維的發展。

師：首先出場的是青蛙。青蛙使勁一跳，誰能說說小青蛙跳了幾格？

生：一格。

師：請大家看畫面，一格是多遠呢？

生：1 分米。

師：一米是10 分米，1 分米如果用分數來表示，是多少呢？

生：十分之一米。

師：同學們，這個十分之一米，也可以用小數0.1米來表示。［2］

片斷磨課二中的每一個問題，都立足于啟發學生的思維及新舊知識的聯系，為學習新知識構筑橋梁。把所要學的新知識放置在整個相關知識體系中，注重知識間的結構和聯系，處理好知識中點與點之間、點與整體之間的關系，善于利用知識間“出生點”“成長點”與“延伸點”。讓學生充分感受數學知識點之間相互銜接，體會部分數學知識點可從不同角度進行分析和理解。

三、開放式提問：遷移方法，融會貫通，發散多種解題思路

學生隨著年齡的增長，課堂發言的積極主動性呈現逐漸下降趨勢，原因是學生的戒備心理在作祟，害怕答錯而丟面子。開放式的提問可以為學生提供廣闊的自由發展空間，讓學生多角度地考慮問題并放松心情投入課堂，能有效解決高年級不管發言的問題。教師要善于利用開放式提問發展學生的思維。

以人教版六年級下冊《圓柱的體積》一課片段教學為例。

師：關于圓柱的體積，你有哪些想知道的問題？

1.大膽猜想：怎樣求圓柱的體積？

猜想1：要求圓柱的體積，和什么有關？為什么？

猜想2：猜猜圓柱的體積計算公式是怎樣的？根據是什么？

2.探究驗證思路：

師：剛才同學們對圓柱體積的計算公式進行各種大膽猜想，那么怎樣驗證這些猜想？你們有自己獨特的想法嗎？先獨立想一想，再在小組內分享自己的想法。

在整個教學活動中，先讓學生大膽猜想圓柱的體積計算方法，然后引導學生利用知識的遷移，化新為舊的轉化思想方法，為探索圓柱的體積公式提供經驗和方法，再由“面”到“體”。［3］通過動手操作，學生發現把圓柱沿直徑切成若干偶數等分，可以拼成近似長方體或正方體。觀察圓柱體轉化為長方體或正方體這一過程的前后變化對比，發現圓柱的形狀發生變化，但體積不變（圖1）。利用轉化思想化新為舊，最后利用長方體體積的公式，推導圓柱體積公式V=sh 或V=πr2×h。

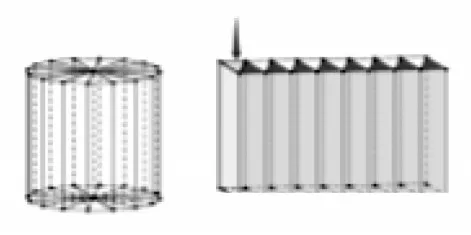
圖1

有學生通過前面的操作，發現當長方體擺放的位置不同時，它們的底面和高發生變化（圖2）。教師引導：想一想，如果不改變擺放位置，還能怎樣求出圓柱體積？學生通過觀察、討論，發現這個長方體的底面與圓柱體側面的關系，剛好是它的一半，高是圓柱底面半徑，得出V=2πr÷2×r×h=πr2×h。

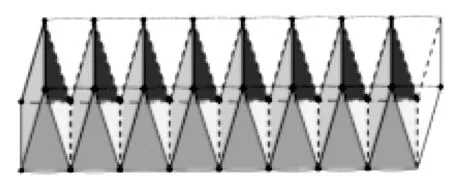
圖2

通過以上兩種不同的方法進行知識梳理，學生懂得融會貫通，避免方法單一片面、死記硬背公式的通病，積累數學活動經驗，增強分析和解決問題的能力。

總之，在具體的教學過程中，教師需從學生的具體情況出發，根據實際情況，把握時機，選擇三種形式的提問策略，逐步引導學生思維的發展。