基于結構化的小學數學深度學習策略
——以人教版四年級上冊“角的度量”教學為例

林宏濱

（廈門市海滄區蕓美小學，福建 廈門 361000）

目前，以學為中心的教學方式發生了許多變化，深層動機、深度理解、高階思維等深度學習方式越來越多地出現在小學數學課堂上。深度學習“深”在哪里？北京師范大學的郭華教授說：深度學習“深”在系統結構中。［1］“結構化”主要是對結構的建構過程的解讀。簡而言之，就是把表象雜亂（復雜）的問題變得結構而有序。深度學習以學習為核心，體現學生在教師的指導下，主動獲取學習經驗、構建新的知識結構、形成新的方法結構、指向高階思維發展的過程，與《義務教育數學課程標準（2011 年版）》中闡釋的數學功能吻合，是學生核心素養形成的基本路徑。

一、結構化對于深度學習的意義

結構化是深度學習的一種途徑，是學習者正確理解數學知識，掌握數學核心概念，培養高層次思維和深層次認知能力的著力點。通過學習知識、方法及思維方面的結構化，學生能夠擁有完整的認知過程，通過知識樣態的建構，幫助學生梳理思維脈絡，明確過程方法，推動情感態度和思維價值的顯著發展。

（一）結構化是深度學習的內涵表達

在學者黎加厚看來：“只有理解學習的目的達到了，深度學習才有基礎可依。隨著對學習的深入，學習者能明確知曉學習過程中出現的一些新思想和新事實，通過對它們的解構和整合，使其豐富自己的認知結構。通過思想間的深度聯系，有助于在新情境中注入學習過的知識，從而保證在新情境中遇到問題時，有助于相應解決對策和建議的提出。”可見，深度學習強調知識的整合、遷移、批判性思維的形成，以及學生如何學習、思考和行動。

（二）結構化是深度學習的發展訴求

深度學習是以解決實際問題為驅動，將學習內容融入原有的認知結構中，實現現有知識在新的問題情境下的合理遷移和成長。［2］結構化的學習方式，能夠幫助學生對學習內容進行梳理，并明確已經學習過的知識間的內在聯系，推動知識框架認知系統的建立，更容易幫助學生全面掌握相應知識。結構化的學習方法和學生的認知步調相統一，在理解和掌握上也相對容易，有助于推動深度學習形式的誕生。

1.從教而言：契合數學教育的新視角

隨著時代的變遷，人們對數學教育的研究重點產生不同的認識。以學習者為主體，以融入知識結構的情境問題驅動為課程教學資源，以“先學后教，以學為主”為教學規則，引導學習者自主地卷入深度學習的新型課堂教學結構，逐漸成為主流趨勢。當下，許多教師都偏向于了解數學知識結構，并通過與學生認知結構的結合，推動數學教學內容的組織和設計。深度學習的教學邏輯，也是讓學生從最初的以“學會”為目標轉變為最后的“愛學”。

2.就學來講：推進深度學習的新發展

深度學習的主要目的是培養學生的學科核心素養。教師需要設計反映學科知識本質的核心問題，形成具有挑戰性和反映學科本質的結構化問題。學生不僅要積累知識、經驗和方法，而且要以某種方式把它們內部“組織”起來。學生對學習內容進行整理、分類、連接、整合等一系列“組織”過程，將知識點連接成知識線，將知識線編成知識網絡，形成具有相關性的知識結構。這種結構有利于遷移、構建和交流知識之間的聯系，滲透思維方法，形成數學思維模式。

二、結構化教學，讓“教”與“學”走向深度

結構化教學是指以挖掘數學知識本質為抓手，以整體建構方法結構為特征，以發展思維為導向，以培養數學學科核心素養為目標的教學方式方法。［3］在教學過程中，如何幫助學生高質量地完成結構化關聯，建構知識系統，實現深度學習？以人教版小學數學四年級上冊“角的度量”一課的教學為例，揭示結構化教與學的內在關聯，明晰結構化教與學的特征，探尋結構化教與學的實踐策略，讓學生知識結構化、方法結構化、思維結構化，最終走向深度學習。

（一）知識結構化：深度建構知識整體樣態，促進主動學習

結構化最初的內涵是指明確結構領域內不同要素之間的關系。布魯納指出：要想明確掌握事物的結構，就需要聯想到其他和事務有關的東西，從而有意識的將兩者聯系在一起，增強自身的理解技能。知識的結構化是從知識的原本性內涵出發，注重知識結構的整體形態，通過學習內容各關鍵要素的關聯分析，不斷豐富學習內容的內涵和外延，從而實現讓學生學到的散點知識連成一條條線，形成由顯而隱、由形而數、由表而里的結構理解，再到反向的如由內而外等的深度建構。

例如，“角的度量”的教學本質是度量。就整個小學階段的數學學習來看，度量是一個持續的學習內容。通過對人教版教材編排的分析和整理，形成如下表格（如表1 所示）：

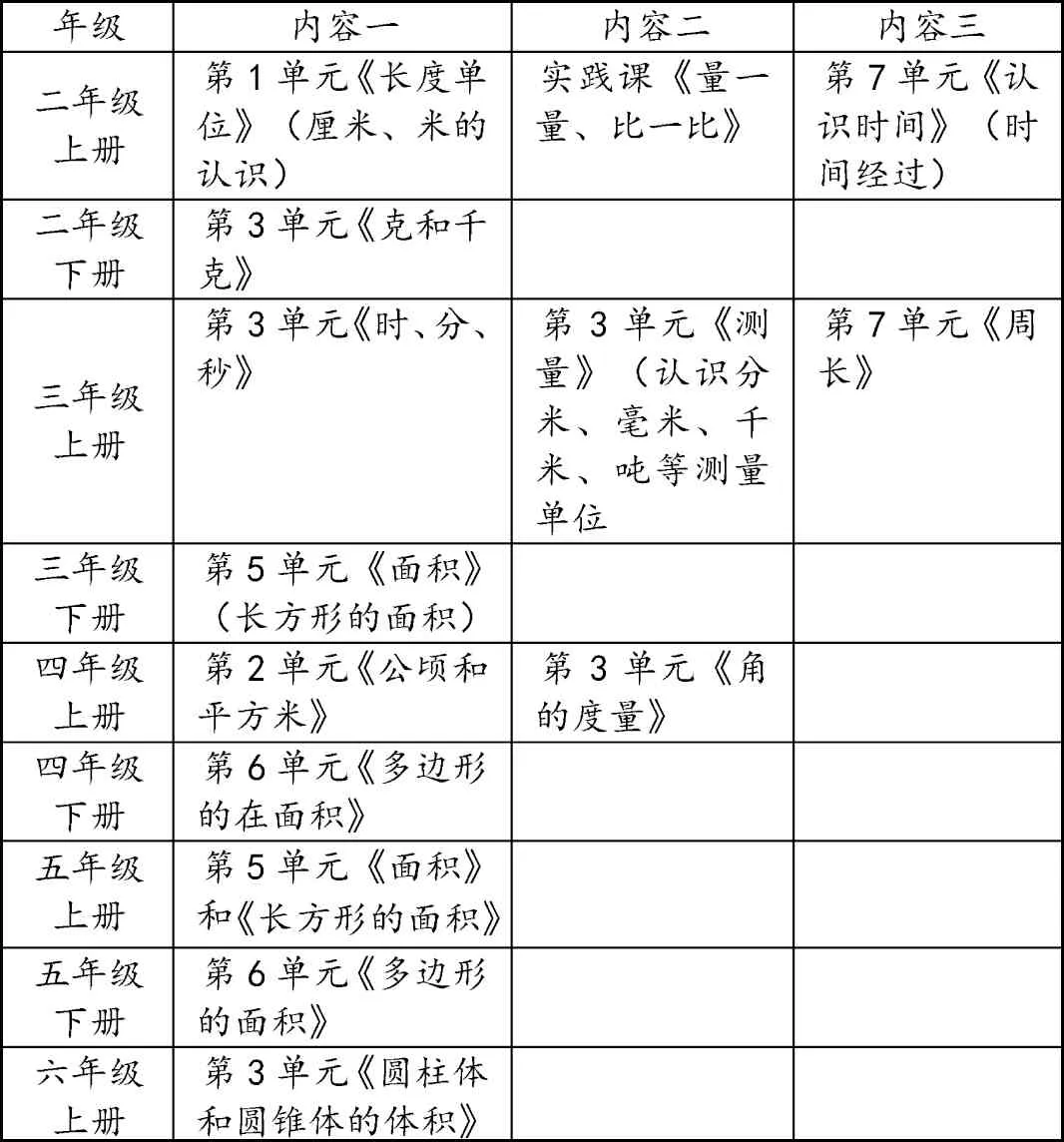
表1 人教版小學數學測量領域教材編排表

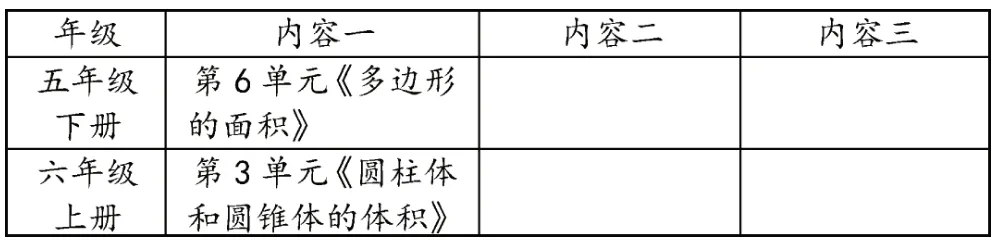
（續上表）

上述編排，可以清楚地看到《角的度量》在人教版四年級上冊，但學生在二、三年級已經學習了長度、面積、質量的度量，以后還要學習體積和容積的度量。無論是長度、面積還是質量的度量，在計數時都有自己的度量單位。此外，“角”的度量在計數時也有自己的度量單位，其度量本質也是計數有幾個度量單位，這一學習理念完全符合學生之前學過的相應內容。所以在學習“角的度量”課前，有必要幫助學生深度建構“度量”的知識結構。再通過知識內容的喚醒、遷移、融通，緊扣知識本質認識和理解1°是一個度量單位，實現知識的正遷移，促進學生對知識結構的學習和理解，形成知識的完整樣態。［4］通過結構化的運用，促進知識的學習。這種方法在整個小學數學學習過程中隨處可見，比如商不變的規律、分數基本性質、整數乘法等的解讀、理解、運用，這些知識都是之前學過的。當這些知識運用到結構化過程中后，教師怎樣確定哪種知識屬于主干知識呢？它們和其他知識之間的聯系點在哪里？如何溝通它們之間的聯系與區別？需要悟其本質、抓其關鍵進行串聯處理，方可將其納入知識體系里。這種學習方式，不僅在形上給予學習脈絡，更幫助學生在本上感悟內容本質，深度建構知識整體樣態，促進學生的主動學習。

（二）方法結構化：深度經歷方法統一過程，促進深度加工

在深度學習中，不能忽視方法的結構化運用，方法結構化要貫穿深度學習的始末。運用方法結構化，能明確如何進行學習操作，并促進知識結構的內化學習。學生在學習一類數學知識時，通常使用相同的學習方法，教師應研究教材中所包含的思想、方法和策略，幫助學生經歷心理發展和數學邏輯發展的完整過程。線編成網，達成方法建構，在深度經歷完整認知過程中掌握知識結構，形成靈活有用的方法結構。

例如，在講授“角的度量”時，教師提問：“怎樣才能知道這條線段的長度呢？”（如圖1）

生：用尺子量。

師：這是一把小尺子，它的長度剛好是1 分米（演示測量）。

生：老師量了4 次，每次是1 分米，所以這條線段長4 分米。

師：用1 平方分米的度量單位量長方形（演示測量），最終能夠求出的面積是多少？

生：老師用1 平方分米的面積單位量了3 次，所以它的面積是3 平方分米。

師：如果我們想知道這個角有多大，應該怎么辦？

本課導課環節，以“度量”的問題為載體，遷移應用到解決“角的度量”問題。教師借助長度、面積的度量，促進學生度量方法的融通，通過長度度量和面積度量的關系分析，幫助學生形成度量方法結構化，深度感悟“計數有幾個度量單位”的本質方法。“角的度量”的學習不僅僅是一個新知的學習，而且與長度、面積、質量度量乃至后續將要學習的體積等度量融為一體，形成有機的方法結構，幫助學生建立清晰整體的知識體系，獲得統一的方法結構。在學習數學的過程中，不僅要明確知識的結構點，也要清晰梳理知識的脈絡。教師要幫助學生把原本鑲嵌在教材豐富背景下的零散方法串聯起來，以結構關聯的模型保存在學生的大腦里，方便以后學習中便捷、有效地提取與轉化，這也是升華數學素養、形成深度學習的有效途徑。

（三）思維結構化：深度明晰思維完整脈絡，促進融會貫通

《義務教育數學課程標準（2011 年版）》指出：“數學在培養人的思維能力和創新能力方面有不可替代的作用。”［5］思維結構化是把表象雜亂的問題變得結構而有序的思維工具，有利于掌握數學學習的全過程，建立數學教學的內部秩序，促進學生認知結構的內部成長。思維結構化需要運用到數學知識建構過程和數學思維發展方式，通過兩者間的緊密配合和融會貫通，促進多維立體結構化學習模型的形成，有助于了解思維的整體脈絡，從而推動深度學習。

教學“角的度量”一課中，教師呈現圖2 中兩種不同的度量方法，追問：“圖中A 和B 兩種量法，哪種是對的？你是怎么想的？”學生經歷了長度、面積度量方法的融通，以及用1 度小角估3°角、10°角，用10°角估30°、50°角的學習過程，建構了度量的知識結構，初步感悟了度量的方法，加之教師引導學生對長度、面積、角等三種度量方法的回顧，角的度量方法思維的結構已經初步形成。這樣的學習不僅停留在“動手、動腦”，更經歷單、雙向思維到立體思維的轉變，使思維的“線”編成“網”。深刻體會知識結構與方法結構的變與不變之間的辯證關系，“度量的方法”自然成為學生的有感而發。學生通過對數學知識邏輯關系的深度思考，有助于促進自身思維脈絡結構的形成。

在數學學習中，學生不僅需要有一定的學習邏輯，還要有學習體系和數形演繹能力。數學結構本身極具嚴謹性，結構化的形成，更需要將數學教學作為一個整體，全面考慮，有序推動教學目標的實施。數學結構以學習的主動建構為支撐，但離不開動態的跟進和成長過程。對教師而言，需要通過對系統化知識結構的運用，明確具體的方法結構和思維脈絡，并以此為基礎，促進學生認知結構的完善和發展，從而提升學生在學習新知識時的表現能力和自我生長能力。