數學教育對比實驗：軟件操作、結果顯示及數據解讀*

胡典順

(華中師范大學數學與統計學學院 430079)

近年來，實證研究愈來愈受到教育研究者的重視，因為這是提升教育科學研究水平并且與國際教育研究接軌的必由之路[1]．數學教育實驗研究中有一類應用很廣泛的研究——對比研究，可以是樣本之間的對比，不同水平的對比，教學干預后的對比分析，也可以是不同教學方法實施后的教學效果對比等．對比研究不僅是數學教育研究者喜歡的一種研究方式，而且也是中小學數學教師方便實施的一種研究方式．但不少人在進行對比研究的時候，研究結論的得出僅從主觀感知的角度去辨析，憑經驗，隨意性很強，不是科學地、規范地通過數據分析，導致研究結論泛化，沒有反映研究問題的特質．研究推理過程也沒有層層遞進的邏輯關聯，研究結果往往不能讓人信服．科學的、規范的數學教育實驗研究應該基于數據，基于對數據的正確解讀，這樣的研究不僅結論可信，他人也可以進行實驗驗證．張奠宙先生在評價范良火教授的論著《教師教學知識發展研究》時稱：“論文得出的是科學結論，并非憑空想象．這種學術研究得出的科學結論，是不能隨便推翻的．”[2]正是因為科學的結論并非憑空想象，不能隨便推翻，數學教育研究要體現“科學化”，提倡研究范式的改變是十分必要的．

本文選取的三個案例中，配對樣本t檢驗要求差值符合正態分布，方差分析的條件是獨立性、正態性和方差齊性．在討論三種分析方法的過程中可能并未涉及這些條件的驗證，另外數據樣本較少，均是為了節省篇幅．本文重點介紹SPSS26.0軟件操作、結果顯示及數據解讀．

1 前測與后測

在對連續變量的推斷統計中，最常用的有t檢驗和方差分析．t檢驗又有單樣本t檢驗，獨立樣本t檢驗以及配對樣本t檢驗，它們都可以用于檢驗兩個總體間連續變量．例1是一種典型的干預前后配對設計，在數學教育實驗中經常遇到．

例1某教師采用教學干預減輕12名學生的數學焦慮，教學干預前后的數學成績數據如表1所示，問教學干預是否有效果？

表1 前后測數據

操作步驟：

(1)根據表1在SPSS26.0中構建數據文件．

(2)點擊【分析】、【比較平均值】、【成對樣本t檢驗】，彈出【成對樣本t檢驗】對話框，將左側框中的前測，點擊添加到右側框中配對1中【變量1】．將左側框中的后測，點擊添加到右側框中配對1中【變量2】中．

(3)在主對話框中點擊【確定】按鈕．

主要結果顯示與解讀：

配對樣本統計平均值個案數標準 偏差標準 誤差平均值配對 1干預前59.501211.3343.272干預后68.50128.5762.476

配對樣本統計中，顯示了教學干預前后的平均值、個案數和標準差，從平均值主觀感知教學干預可能有效果，但有待假設檢驗進行驗證．

配對樣本相關性個案數相關性顯著性配對 1干預前 & 干預后12.614.033

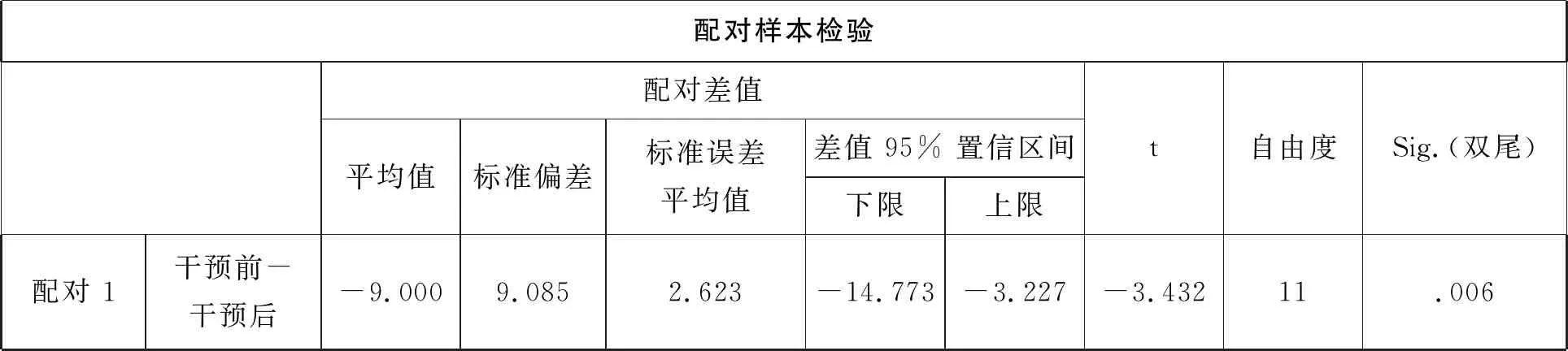
配對樣本檢驗配對差值平均值標準偏差標準誤差平均值差值 95% 置信區間下限上限t自由度Sig.(雙尾)配對 1干預前- 干預后 -9.0009.0852.623-14.773-3.227-3.43211.006

配對樣本相關性和配對樣本檢驗中0.033，0.006，均小于0.05，說明數據一致性好，差異有統計學意義，并且差異的產生就是教學干預因素作用的結果．

2 重復測量

重復測量是指對同一批受試對象的同一觀測指標在不同時間點上進行多次測量，其目的是觀察不同時間點的動態變化趨勢特征．[3]在數學教育實驗研究中，由于各種原因需要對觀察樣本進行多次觀測，而不僅僅只有前測和后測．重復測量在數學教育實踐中是大量存在的．例2討論兩因素重復測量，對單因素重復測量，不等距重復測量等本文不作討論．

例2某教師為了調查某種新的教學方法對數學成績的影響．該教師在兩個學習小組隨機抽取了12名學生，第一個學習小組按新的教學方法教學，第二個學習小組不用新的教學方法，并于實驗開始的第1、2、3個月分別測量學生的數學成績，數學成績如表2所示，問新的教學方法是否有效果？

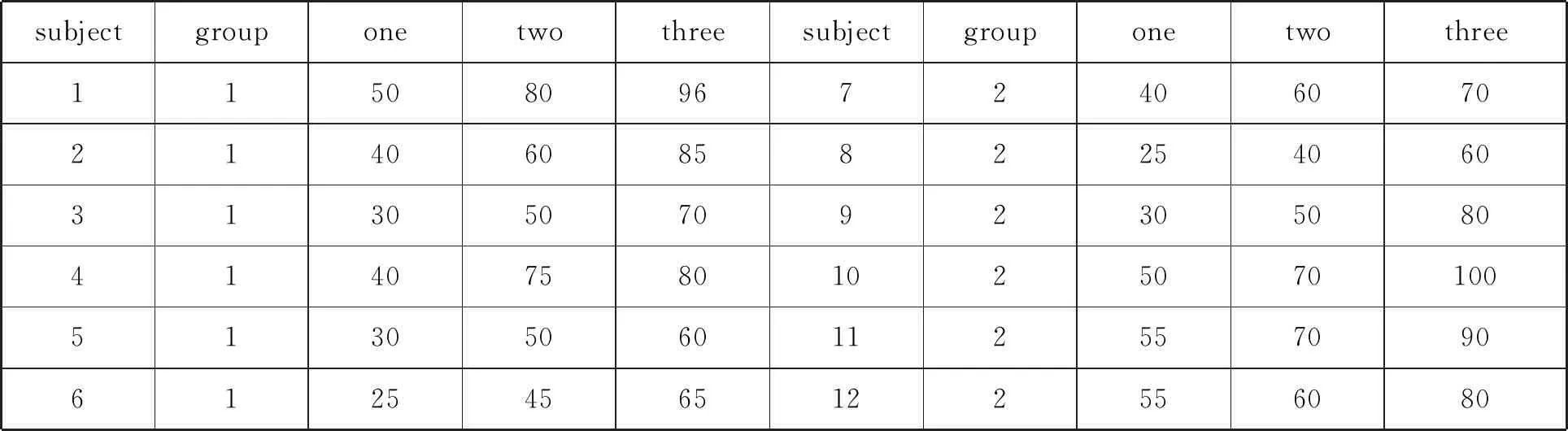
表2 三次測量成績

操作步驟：

(1)根據表2在SPSS26.0中構建數據文件．

(2)點擊【分析】、【一般線性模型】、【重復測量】，彈出【重復測量定義因子】對話框，將【主體間因子】中的【因子1】改為【time】．

(3)【級別數】框中輸入重復測量次數【3】，點擊【添加】按鈕．

(4)點擊左下角的【定義】按鈕，將3次測量變量one，two，three按照框中測量的順序，逐個放入右側框中，次序不能出錯．

(5)將單變量group放入【主體間因子】框．

(6)點擊【模型】按鈕，在彈出對話框中，選擇【全因子】模型，點擊【繼續】按鈕．

(7)點擊【選項】按鈕，在彈出對話框中，勾選【描述統計】、【齊性檢驗】，點擊【繼續】按鈕．

(8)在主對話框中點擊【確定】按鈕．

主要結果顯示與解讀：

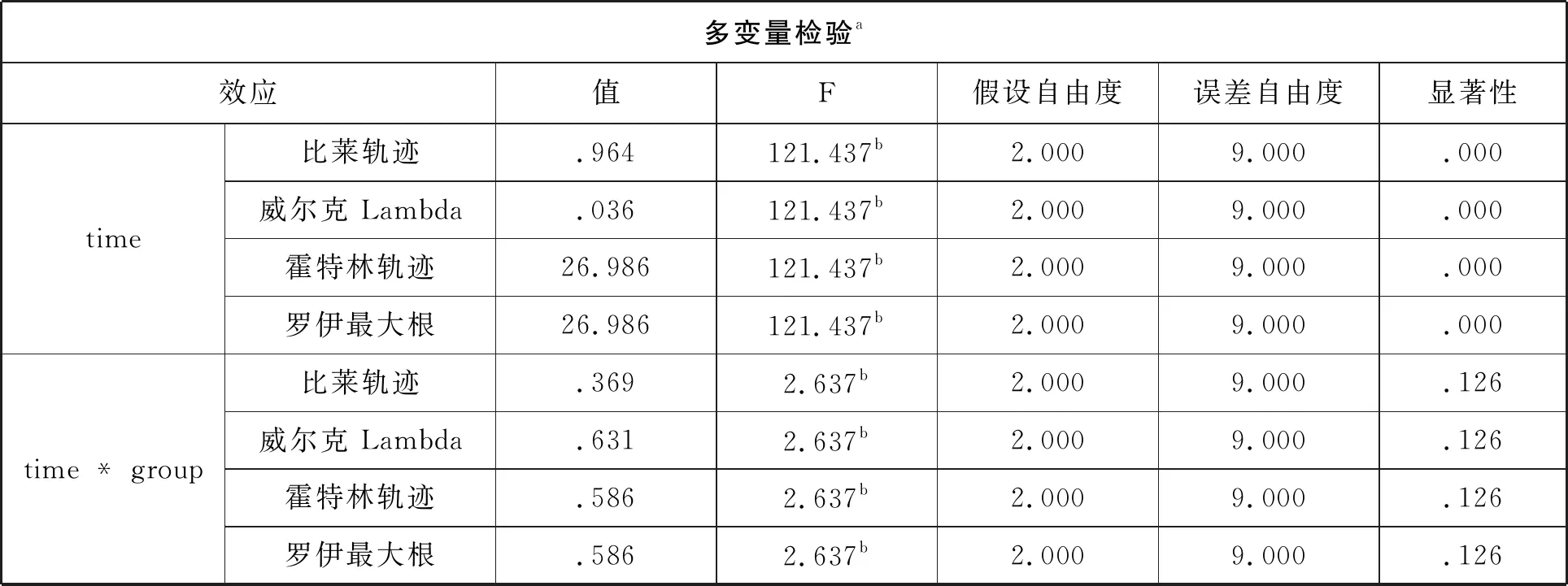
多變量檢驗a效應值F假設自由度誤差自由度顯著性time比萊軌跡.964121.437b2.0009.000.000威爾克 Lambda.036121.437b2.0009.000.000霍特林軌跡26.986121.437b2.0009.000.000羅伊最大根26.986121.437b2.0009.000.000time * group比萊軌跡.3692.637b2.0009.000.126威爾克 Lambda.6312.637b2.0009.000.126霍特林軌跡.5862.637b2.0009.000.126羅伊最大根.5862.637b2.0009.000.126

多變量檢驗．多變量檢驗是一種多元分析方法，其中采用了4種檢驗方法進行計算．表中P=0.000<0.05，多變量結果認為，數學成績隨時間發生趨勢性變化，存在差異性．time * group交互作用中，P=0.126>0.05，group與time不存在交互作用．

莫奇來球形度檢驗a測量: MEASURE_1 主體內效應莫奇來 W近似卡方自由度顯著性Epsilonb格林豪斯-蓋斯勒辛-費德特下限time.895.9942.608.9051.000.500

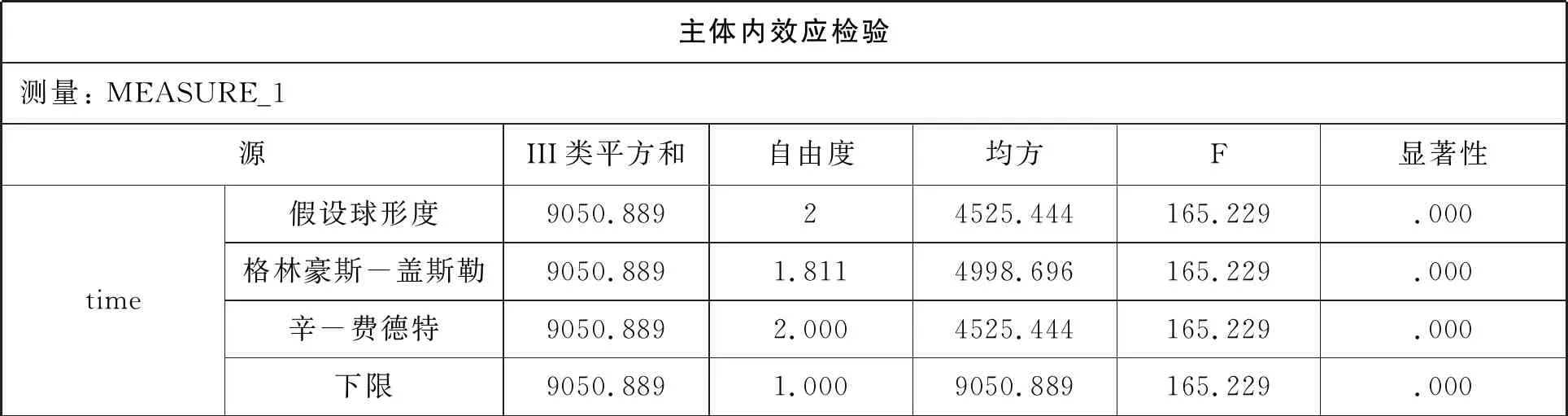
主體內效應檢驗測量: MEASURE_1源III類平方和自由度均方F顯著性time假設球形度9050.88924525.444165.229.000格林豪斯-蓋斯勒9050.8891.8114998.696165.229.000辛-費德特9050.8892.0004525.444165.229.000下限9050.8891.0009050.889165.229.000

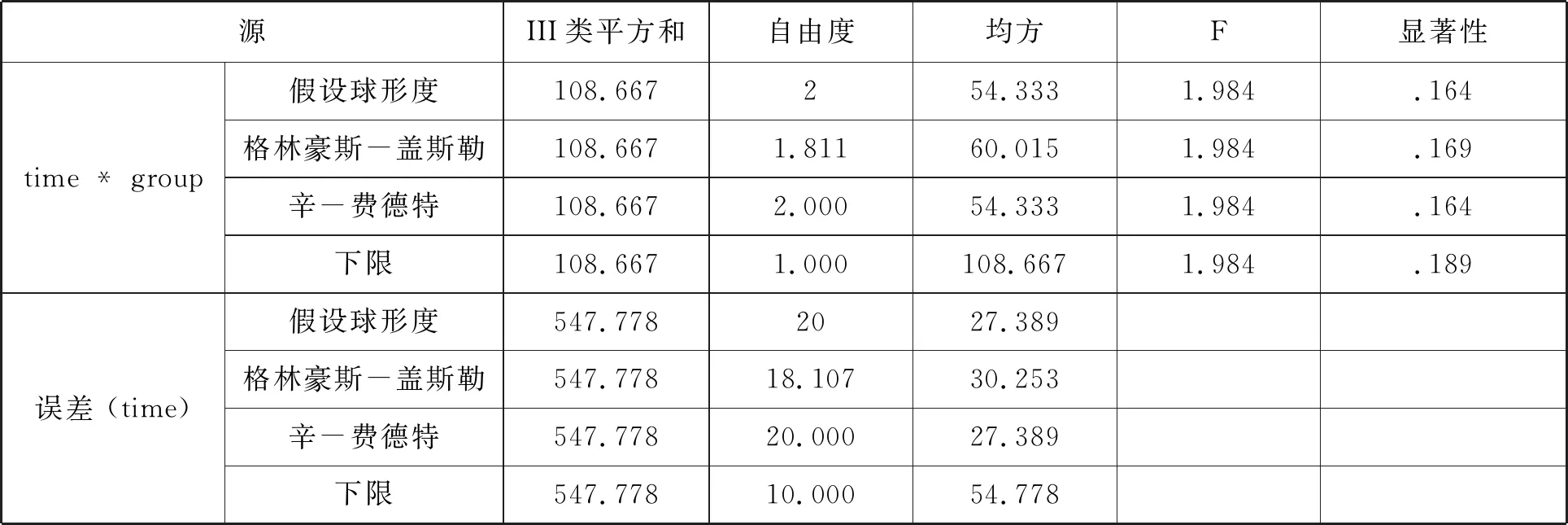
續表

球對稱與主體內效應．顯著性P=0.608>0.05，符合球對稱性．既然符合球對稱，可以進行單變量重復測量方差分析．因為符合球對稱，主體內檢驗看“假設球形度”結果，F=165.229，P=0.000<0.05，認為數學成績變化具有時間變化趨勢．time * group交互作用中，F=1.984，P=0.164>0.05，group與time不存在交互作用．這里的結果與多變量結果一致，更加說明結果可靠．

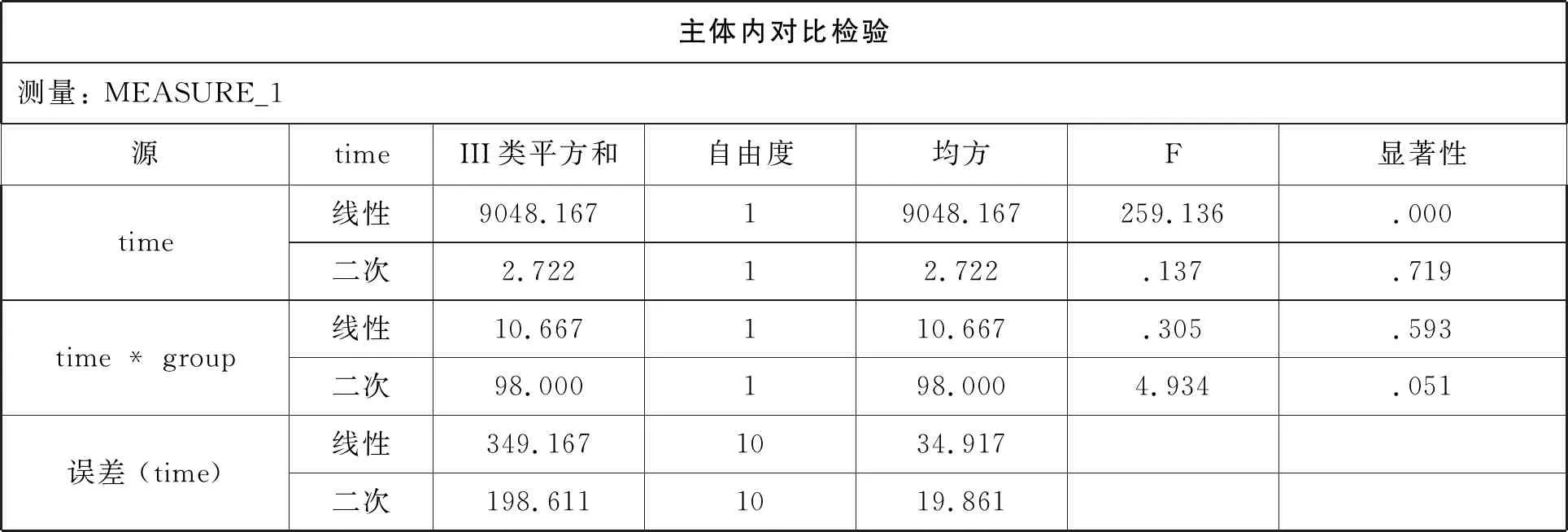
主體內對比檢驗測量: MEASURE_1源timeIII類平方和自由度均方F顯著性time線性9048.16719048.167259.136.000二次2.72212.722.137.719time * group線性10.667110.667.305.593二次98.000198.0004.934.051誤差 (time)線性349.1671034.917二次198.6111019.861

主體內對比檢驗．既然不同時間存在差異，那么會存在什么趨勢性的變化呢？對于time，P=0.000<0.05，發現線性有意義，P=0.719>0.05，發現二次無意義．對于time * group，P=0.5934>0.05，P=0.051>0.05，線性、二次都無意義．因此，可以認為數學成績變化符合線性關系．

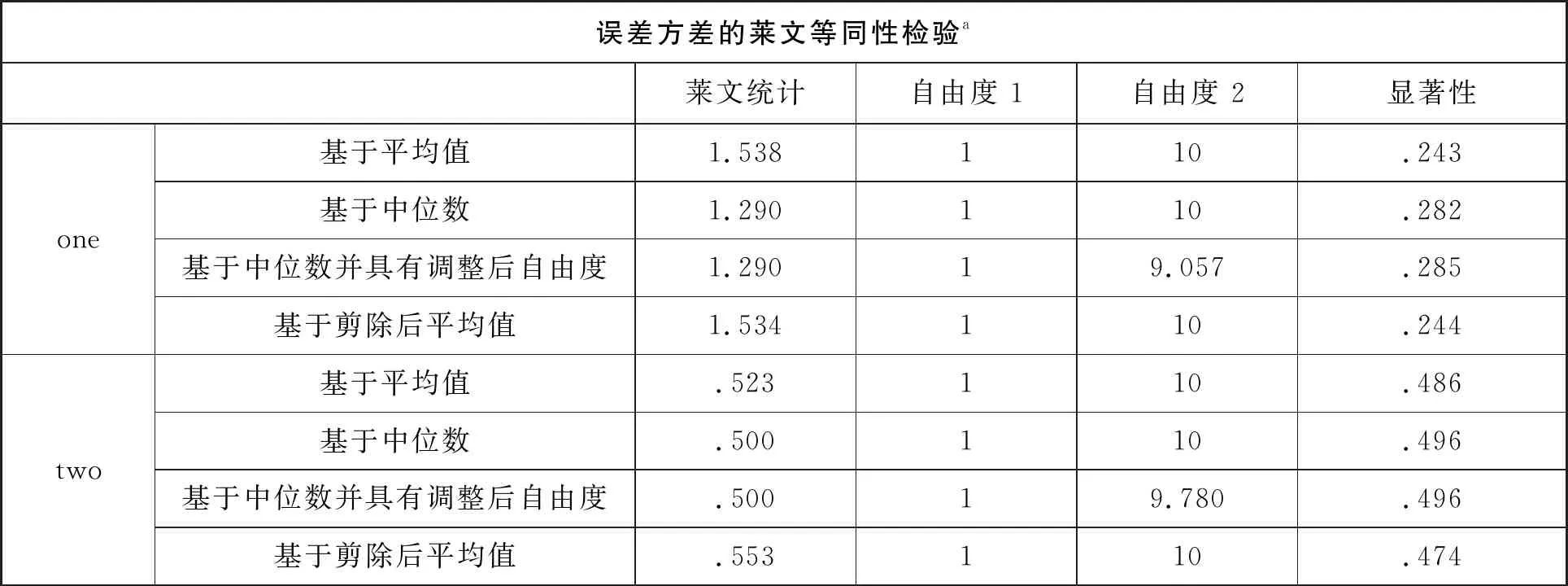
誤差方差的萊文等同性檢驗a萊文統計自由度 1自由度 2顯著性one基于平均值1.538110.243基于中位數1.290110.282基于中位數并具有調整后自由度1.29019.057.285基于剪除后平均值1.534110.244two基于平均值.523110.486基于中位數.500110.496基于中位數并具有調整后自由度.50019.780.496基于剪除后平均值.553110.474

續表

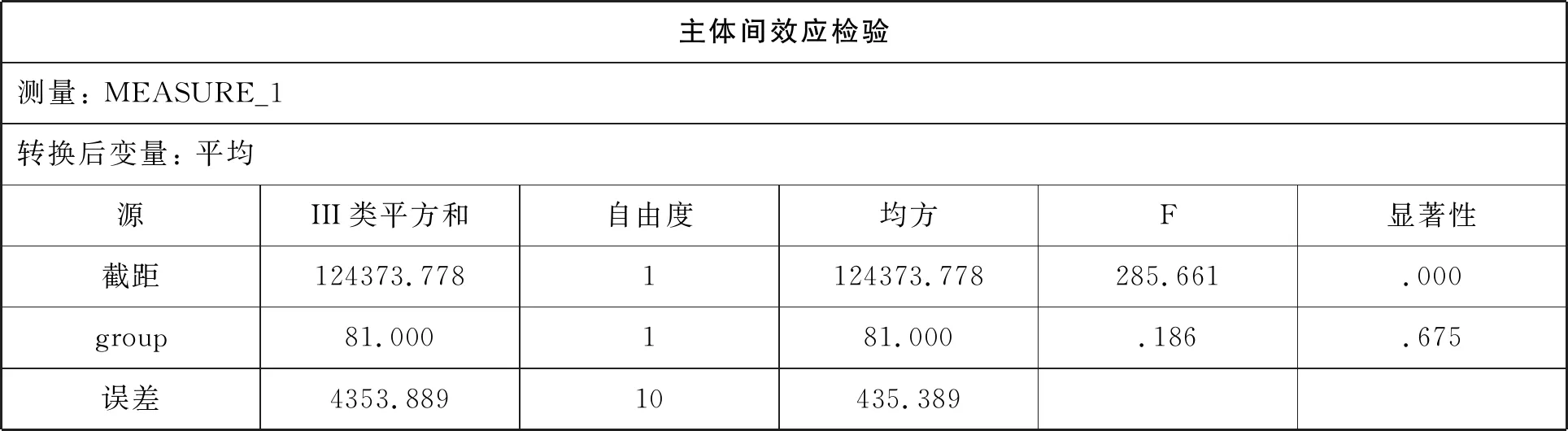
主體間效應檢驗測量: MEASURE_1轉換后變量: 平均 源III類平方和自由度均方F顯著性截距124373.7781124373.778285.661.000group81.000181.000.186.675誤差4353.88910435.389

需要指出的是，本例中，由于time * group無交互，分析較為簡單，只要得到time有無統計意義，group有無統計意義，基本就能達到分析的目的．但當time * group存在交互時，time、 group都受另一因素的影響，因此分析就要復雜得多．限于篇幅，這種情形的分析本文不作討論．

3 嵌套設計

當考慮的因素之間存在層次性結構，即嵌套結構的每一層次都是上一層次的細化，或者各個實驗因素的影響根據專業知識有主次之分，次要因素的各個水平嵌套在主要因素的水平下時，這時所做的設計常為嵌套設計．[4]在數學教育研究中，有二因素嵌套設計、三因素嵌套設計等．例3是三因素嵌套設計，有“學校”和“班級”兩個嵌套變量，8個“班級”嵌套在4個“學校”中，4個“學校”雙嵌套在兩種“教學方法”中．

例3某研究者為了研究兩種教學方法的效果，隨機選擇了4所學校，每個學校選擇2個班級，隨機分配2個學校的4個班級用第一種教學方法，另外兩個學校的4個班級用第二種教學方法，表格中數據是學生成績，數據如表3所示，試對教學方法做差異分析．(此例根據武松編著《SPSS實戰與統計思維》一書P174頁例子改編而成)

表3 兩種教學方法效果比較

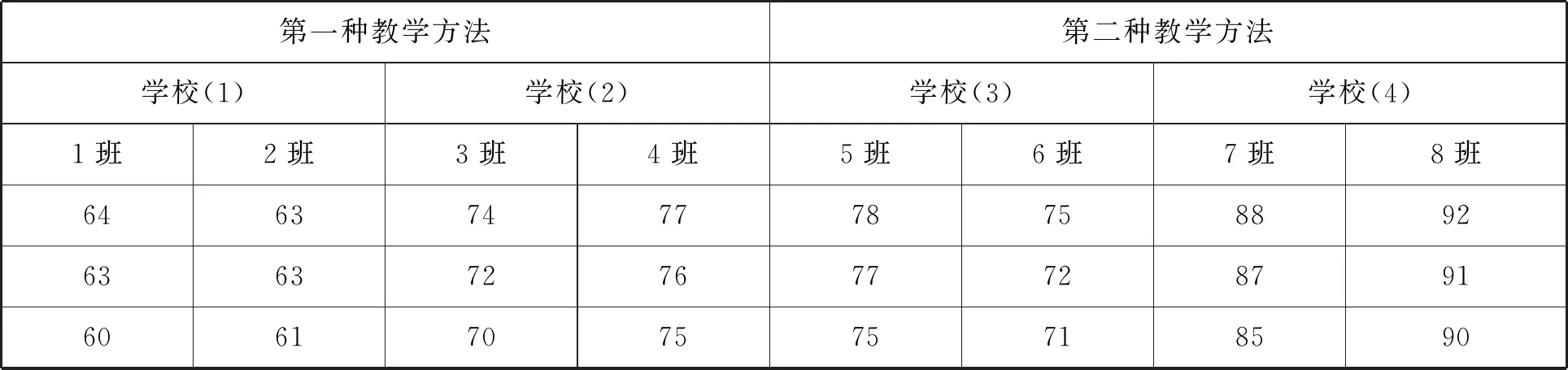
續表

操作步驟：

(1)根據表3在SPSS26.0中構建數據文件．

(2)點擊【分析】、【一般線性模型】、【單變量】，將成績放入【因變量】對話框，將教學方法、學校和班級放入【固定因子】框中．

(3)點擊【模型】，選定【構建項】，將教學方法、學校和班級放入【模型】框中，將【類型】中的【交互】改為【主效應】，點擊【繼續】．

(4)點擊【選項】按鈕，勾選【描述統計】、【F檢驗】，點擊【繼續】．

(5)點擊【粘貼】按鈕，得到操作的程序，將原來的程序(左)修改為程序(右)：

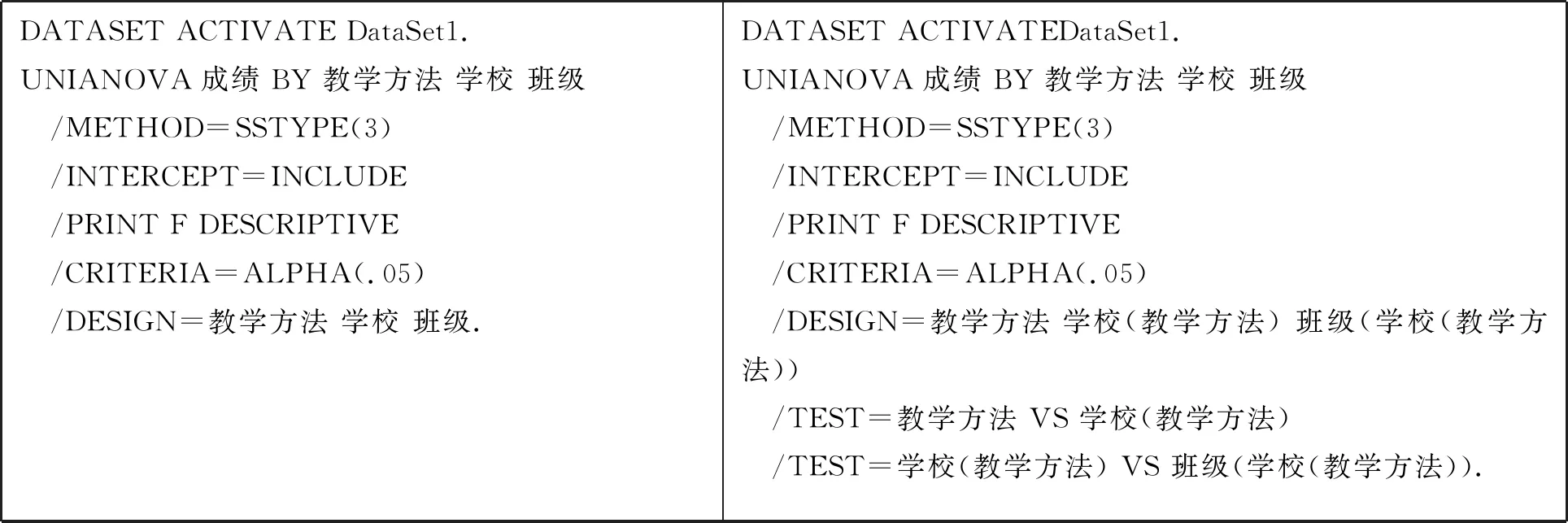
DATASET ACTIVATE DataSet1.UNIANOVA成績 BY 教學方法 學校 班級 /METHOD=SSTYPE(3) /INTERCEPT=INCLUDE /PRINT F DESCRIPTIVE /CRITERIA=ALPHA(.05) /DESIGN=教學方法 學校 班級.DATASET ACTIVATEDataSet1.UNIANOVA成績 BY 教學方法 學校 班級 /METHOD=SSTYPE(3) /INTERCEPT=INCLUDE /PRINT F DESCRIPTIVE /CRITERIA=ALPHA(.05) /DESIGN=教學方法 學校(教學方法) 班級(學校(教學方法)) /TEST=教學方法 VS 學校(教學方法) /TEST=學校(教學方法) VS 班級(學校(教學方法)).

修改完畢，點擊菜單【運行-全部】，運行程序．

主要結果顯示與解讀：

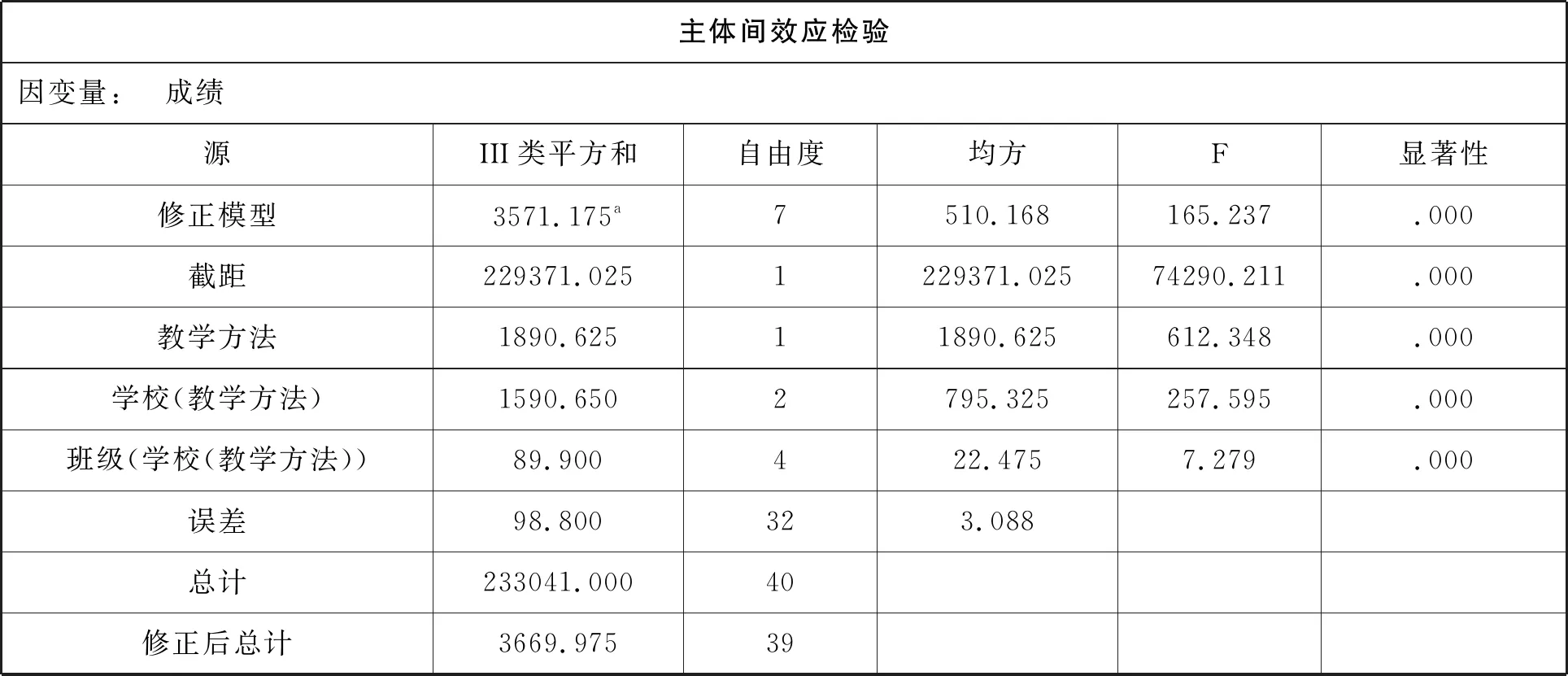
主體間效應檢驗因變量: 成績 源III類平方和自由度均方F顯著性修正模型3571.175a7510.168165.237.000截距229371.0251229371.02574290.211.000教學方法1890.62511890.625612.348.000學校(教學方法)1590.6502795.325257.595.000班級(學校(教學方法))89.900422.4757.279.000誤差98.800323.088總計233041.00040修正后總計3669.97539

主體間效應檢驗中，只反映不同班級的成績有無統計學意義．由于F=7.279，P=0.000<0.05，因而，不同班級之間差異有統計學意義．

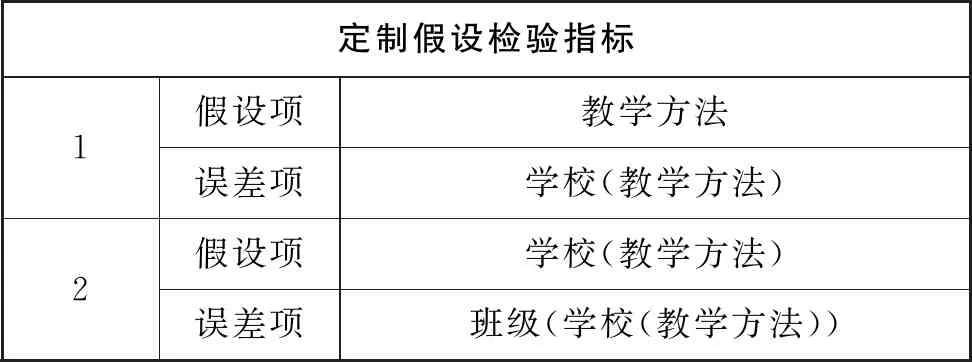
定制假設檢驗指標1假設項教學方法誤差項學校(教學方法)2假設項學校(教學方法)誤差項班級(學校(教學方法))

定制假設檢驗 1

檢驗結果因變量: 成績源平方和自由度均方F顯著性對比1890.62511890.6252.377.263誤差a1590.6502795.325

定制假設檢驗1中，反映不同教學方法學生的成績有無統計學意義．由于F=2.377，P=0.263>0.05，因而，不同教學方法學生的成績差異無統計學意義．

定制假設檢驗2

檢驗結果因變量: 成績源平方和自由度均方F顯著性對比1590.6502795.32535.387.003誤差a89.900422.475

定制假設檢驗2中，反映不同學校學生的成績有無統計學意義．由于F=35.387，P=0.003<0.05，因而，不同學校學生的成績差異有統計學意義．

4 結語

數學教育研究中，不能否認的是，無論是碩博畢業論文的撰寫，還是教研論文的發表，依然存在經驗描述和概括總結、缺乏證據的空泛討論，理論移植加數學實例，泛學科的空洞議論等現象，導致的后果是理論泛化，證據缺失，偏離學科研究特質．數學教育研究要真正做到“有理有據”“言必有據”，在研究中就始終要有“數據與證據”意識．在研究過程中不斷追問自己——我是如何進行研究設計的？采用的研究方法是什么？數據是如何收集的？收集了哪些數據？論證過程是不是基于證據的推理？有沒有層層遞進的邏輯關聯？研究結論有哪些支持證據？等等．這樣的數學教育研究才是科學的、規范的，才應該是數學教育研究所倡導的研究范式．