條件概率的弱定義與隨機事件間相依性的不同刻畫
李興東,楊 剛
(蘭州交通大學 數(shù)理學院,蘭州 730070)
隨機事件之間及隨機變量之間相依性及其度量,是概率統(tǒng)計中重要的研究課題之一.正如我國著名概率統(tǒng)計專家張堯庭教授所言,本文可引出許多隨機變量之間相依性的指標,本文從不同的角度給出相依性的度量,并應盡快將這些內(nèi)容吸收到統(tǒng)計教材中來[1-2].目前,文獻[3-8]研究了Pearson相關系數(shù)、Kendall相依系數(shù)、Spearman秩相依系數(shù)等相依性度量指標的性質(zhì)及其應用,這些相依性指標是隨機變量間或隨機向量間整體相依性的不同刻畫及其度量.
因此,要準確地對復雜的相依性給出或微觀或局部的度量,一條可行的途徑就是首先探明隨機事件間的相依性及其度量,然后將其方法與思路及其所得結論再拓展到隨機變量間及隨機向量間的相依性及其度量.條件概率是揭示隨機事件之間及隨機變量或隨機變量序列之間相依性及其度量的基本工具[9],因條件概率正是從一隨機事件的發(fā)生對另一事件發(fā)生的可能性的影響入手考慮相依性及其度量的.為能深入揭示相依性及其度量,必須對條件概率深入探討.

事實上,概率為0的事件分為兩類[11],概率為0的事件包含了不可能事件,不同于不可能事件,卻常被誤認為不可能事件.比如,在區(qū)間[0,1]上“取到有理數(shù)”的概率為0,但不是不可能事件.
本文中,首先將條件概率的定義進行推廣,事件B可以是概率為0的事件,從而事件B為任意事件,A,B也就為任意兩事件.為此,證明以下3個命題.
命題1設(Ω,F,P)是一個概率空間,對任意A,B∈F,則max{0,P(A)+P(B)-1}≤P(AB)≤min{P(A),P(B)}.
證明因A,B是概率空間(Ω,F,P)的任意兩事件.一方面,因A∪B?Ω,由概率加法公式與單調(diào)性,有P(A∪B)=P(A)+P(B)-P(AB)≤P(Ω)=1,得P(AB)≥P(A)+P(B)-1;再由概率的非負性,得P(AB)≥0;故max{0,P(A)+P(B)-1}≤P(AB).
另一方面,因AB?A且AB?B,得P(AB)≤P(A)且P(AB)≤P(B),故P(AB)≤min{P(A),P(B)}.
從而,max{0,P(A)+P(B)-1}≤P(AB)≤min{P(A),P(B)}.
命題1給出了積事件概率不等式,由這個重要不等式,容易證明命題2與命題3也成立.
命題2在概率空間(Ω,F,P)中,若P(B)=0,則對任意事件A,有P(AB)=P(A)P(B),即0=P(A)×0.
命題3在概率空間(Ω,F,P)中,若P(B)=1,則對任意事件A,有P(AB)=P(A)P(B),即P(A)=P(A)×1.
由命題2與命題3,在同一個概率空間中,概率為0的事件、概率為1的事件都與任意事件獨立,這與直觀實際也是吻合的,即概率為0的事件和概率為1的事件都與任意事件獨立,都不影響任意事件發(fā)生的概率.
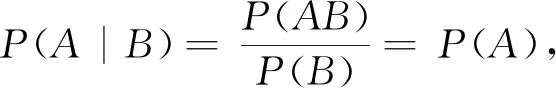
從而,給出條件概率的弱定義.文獻[12]也給出了邊緣密度函數(shù)為0的情形下二維隨機變量的條件分布.
1 條件概率的弱定義
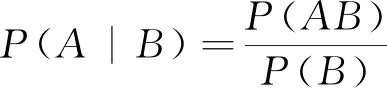
可見,弱定義中A,B是任意兩事件,且允許分母P(B)=0.因此,以條件概率為基礎的乘法公式、貝葉斯公式中都可以推廣為任意事件,下文的事件都可以是任意事件.
接下來,基于積事件概率不等式的3個命題與條件概率的弱定義,進一步提出事件間的相依原理和相依度,從不同角度逐步深入、準確地刻畫任意兩隨機事件之間的相依關系,也推廣了條件概率、獨立性等概念與相關概率命題的適用范圍,使相關結論在具有更大理論價值和實踐價值基礎上,有更完美、對稱的表達形式.
2 從不同角度刻畫任意兩隨機事件之間的相依關系
基于條件概率的弱定義,能定性或定量地給出任意兩隨機事件相依性的不同刻畫.
2.1 任意兩隨機事件相互獨立的定性刻畫
定性的,若同一個概率空間下的一事件的發(fā)生與否不影響另一事件發(fā)生的概率,則稱兩事件相互獨立.在條件概率的弱定義下可以得到任意兩事件相互獨立的定量刻畫或定義:設A,B是概率空間(Ω,F,P)的任意兩事件,若P(AB)=P(A)P(B),則稱A,B相互獨立,簡稱A,B獨立.否則,稱A,B不獨立或相依.這里,A與B都是允許概率為0或1的任意兩事件.
1) 任意兩隨機事件的相依性是相互的
條件概率揭示了任意兩隨機事件的相依關系,且這任意兩事件沒有先后關系或因果關系,是成對出現(xiàn)的,其中的任何一個事件都可作為條件,這是對相依性的樸素認識.
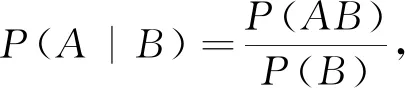
2) 由概率乘法公式刻畫任意兩隨機事件之間的相依關系
設A,B是概率空間(Ω,F,P)的任意兩事件,則P(AB)=P(A|B)P(B)=P(B|A)P(A).
3) 由貝葉斯公式刻畫任意兩隨機事件之間的相依關系
貝葉斯公式的另一種表達形式是:
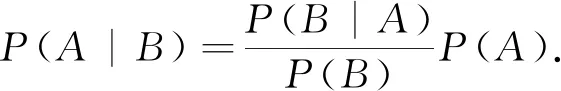
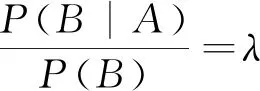
2.2 由似然度定量刻畫任意兩隨機事件之間的相依關系
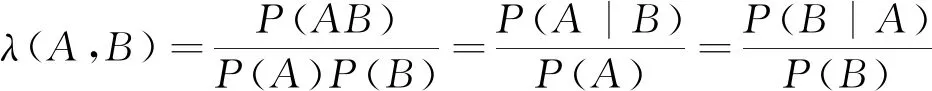
若λ(A,B)<1,則稱A與B負相依;若λ(A,B)=1,則稱A與B不相依(即獨立);若λ(A,B)>1,則稱A與B正相依;
可見,同一個概率空間的任意兩事件A與B的似然度λ,實質(zhì)是集合A與B的二元集函數(shù),且函數(shù)值是非負實數(shù).無論似然度λ取任何非負值,A與B彼此間的作用是相互的λ,似然度有如下性質(zhì).
性質(zhì)1(任意兩事件間的相依原理)設A,B是概率空間(Ω,F,P)的任意兩事件,則有:
1)λ(A,B)=λ(B,A);
2) 任意兩隨機事件或負相依、或不相依、或正相依,三者必具其一且只具其一;

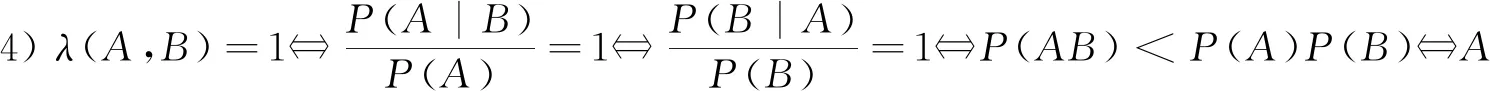


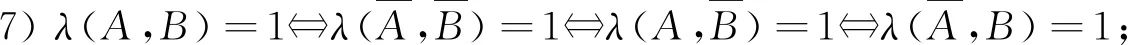
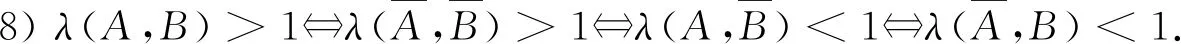

性質(zhì)2設A,B是概率空間(Ω,F,P)的任意兩事件,則有:
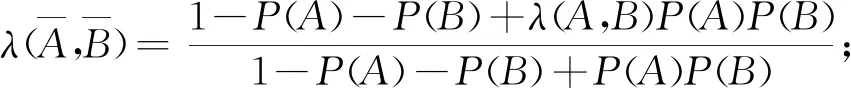
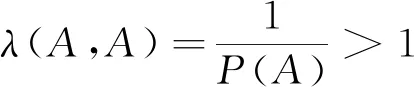
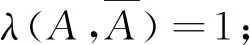
綜上,同一個概率空間下任意兩事件的似然度λ取非負實數(shù)值,定性并定量地刻畫了A與B之間的相依關系:λ∈[0,1)時負相依;λ=1時獨立;λ∈(1,+∞)時正相依.由性質(zhì)2,似然度在區(qū)間[0,+∞)上以1為分界“非對稱”地取值,主要定性地刻畫了事件間的相依關系,但在定量方面,與下文提出的相依度相比有明顯不足.
2.3 由相依度定量刻畫任意兩隨機事件之間的相依關系
事實上,P(AB)-P(A)P(B)的符號(小于0、等于0、大于0)只是定性地反映了A與B是負相依、不相依還是正相依,只是一個絕對數(shù),要相對地反映兩事件相依程度的大小,需要知道P(AB)的最小值和最大值,由命題1,m=max{0,P(A)+P(B)-1}≤P(AB)≤min{P(A),P(B)}=M,因此,分別考慮積事件的概率到獨立時的距離,積事件概率的最值到獨立時的距離,兩者之比能精確地刻畫A與B相依程度的大小,即為A,B的相依度.文獻[13]也給出了隨機變量之間的相依度函數(shù).
定義3設A,B是概率空間(Ω,F,P)的任意兩事件,則稱
ρ(A,B)=
為A,B的相依度.
由相依度的定義,若給定P(A),P(B),則對于在區(qū)間[m,M]中取值的P(AB),閉區(qū)間[-1,1]中存在唯一的相依度ρ(A,B)與之對應,反之亦然.從而,若給定P(A),P(B),則P(AB)與A,B的相依度ρ(A,B)之間存在一一映射關系.
當m≤P(AB) 當P(AB)=P(A)P(B)時,ρ(A,B)=0,稱為不相依,即獨立; 當P(A)P(B) 特別,當P(AB)=m時,ρ(A,B)=-1,稱為完全負相依;當P(AB)=M時,ρ(A,B)=1,稱為完全正相依. 顯然,相依度也是集合A與B的二元集函數(shù).可以驗證,相依度有以下較好性質(zhì): 性質(zhì)3設A,B是概率空間(Ω,F,P)的任意兩事件,則有: 1) -1≤ρ(A,B)≤1; 2)ρ(A,B)=ρ(B,A); 4) |ρ|越小,相依程度越弱;|ρ|越大,相依程度越強;|ρ|=1,相依程度最大; -1. 以下實例,說明了兩事件的似然度、相依度的具體求解,并驗證了性質(zhì)1、性質(zhì)2與性質(zhì)3. 例1在同一個概率空間下,已知P(A)=0.2,P(B)=0.3,并設P(AB)=0.15,分別解答: 1)λ(A,B),ρ(A,B);并說明A,B相依關系; 上文基于條件概率的弱定義,從多個角度定性并定量地逐步深入刻畫了同一個概率空間的任意兩事件的相依性及其度量,并已擴大了相關概率命題的應用范圍,使相關結論在具有更大理論價值和實踐價值基礎上,有更完美、對稱的表達形式.為進一步論證,下文再給出了任意兩事件負相依、不相依、正相依的其他等價刻畫,并結合一個具體實例,說明相關概率命題應用范圍的擴大. 1) 任意兩事件負相依的其他等價刻畫 設A,B是概率空間(Ω,F,P)的任意兩事件,A與B負相依等價于 2) 任意兩事件不相依的其他等價刻畫 設A,B是概率空間(Ω,F,P)的任意兩事件,A與B不相依等價于 3) 任意兩個事件正相依的其他等價刻畫 設A,B是概率空間(Ω,F,P)的任意兩事件,A與B正相依等價于 4) 相關概率命題應用范圍的擴大 現(xiàn)行教材中,條件概率公式、乘法公式、全概率公式、貝葉斯公式中都要求分母大于0.在條件概率的弱定義下,其分母都可以等于0;本文中,其中的事件都是任意事件,既擴大了相關概率命題的應用范圍,又使數(shù)學表達對稱、統(tǒng)一. 本文從條件概率的概念出發(fā),提出了條件概率的弱定義、事件間的相依原理和事件間的相依度,從不同角度逐步深入、準確地刻畫了同一個概率空間的任意兩隨機事件之間的相依關系及其度量,并使建立在條件概率基礎上的相關命題有形式與本質(zhì)的統(tǒng)一. 正如我國著名概率統(tǒng)計專家張堯庭教授所言,本文可引出許多隨機變量之間相依性的指標,從不同的角度給出相依性的度量,并應盡快將這些內(nèi)容吸收到統(tǒng)計教材中來.筆者認為,基于條件概率的弱定義,以相依性為線索,也可以構建概率統(tǒng)計的主要內(nèi)容、方法與原理,在理論方面與實踐方面都具有“潛在”意義.本文從事件的角度作了基礎性的有意義的探索. 基礎性是顯而易見的,有意義表現(xiàn)在:本文給出了兩隨機事件間相依性的不同刻畫及其度量,特別是提出了兩事件的相依度,能較準確地度量兩事件相依程度.本文方法與思路及其所得結論可拓展到隨機變量間及隨機向量間的相依性及其度量,對應的就能得到隨機變量間或隨機向量間相依性的不同刻畫及其度量,相應的相依度與Pearson相關系數(shù)、Kendall相依系數(shù)、Spearman秩相依系數(shù)等相依性度量指標有密切關系,能克服這些度量指標的不足,能適應各種相依類型,較準確地對復雜的相依性給出或微觀或局部或整體的度量.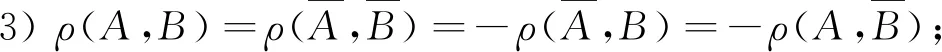

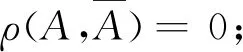
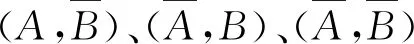
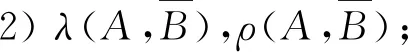
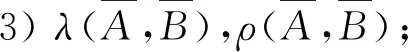
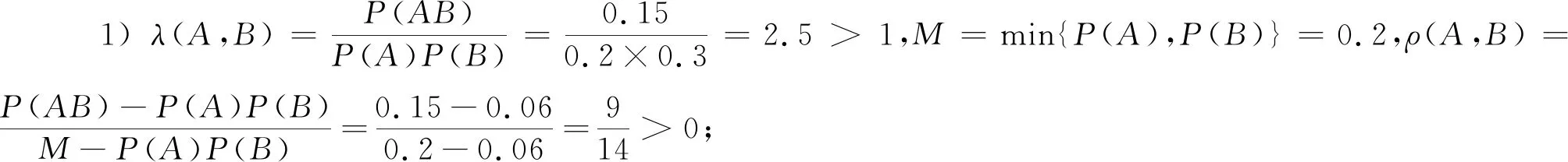
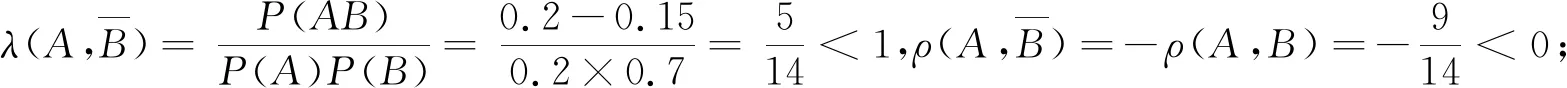
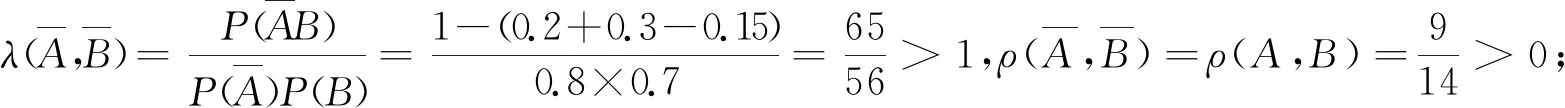
3 相依性的其他等價刻畫與相關概率命題應用范圍的擴大
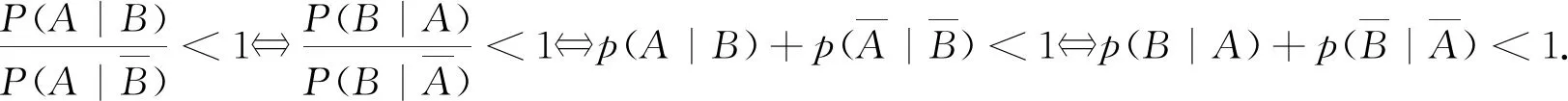
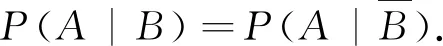
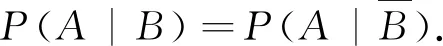

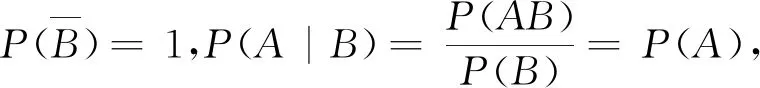
4 結束語

