橢圓方程系數識別問題的正則化解

何 琴，王 謙

(蘭州交通大學 數理學院，蘭州 730070)

橢圓型方程[1-5]是偏微分方程領域內的一個重要分支，是解決很多實際問題的有力工具.從整個區域上的不精確值識別橢圓方程Dirichlet問題中的系數的反問題，這引起了很多學者的極大關注[6-9].由于這些問題是不適定的，已經有幾種穩定的方法來解決他們，其中Tikhonov正則化方法是最著名的方法.雖然有很多論文專門研究這個問題，但是很少有人專門研究這些方法的收斂速度.文獻[10-14]研究了Bregman距離意義下線性不適定問題的凸變分正則化的收斂速度，獲得了全變分正則化的收斂速度.雖然有許多論文使用不適定問題的Tikhonov正則化，但很少有人專門研究收斂速度.Engl等[15]和Kanagaraj等[16]的論文專門討論了上述問題的Tikhonov正則化.這些作者使用輸出最小二乘法和非線性不適定問題的Tikhonov正則化，得到了某些源條件下的收斂速度.但是使用非凸泛函，很難找到全局極小值.在本文中，不使用輸出最小二乘法，而是將Tikhonov正則化方法應用于求解原問題的新能量泛函，獲得該方法的收斂速度.

本文討論了具有齊次邊界Dirichlet橢圓方程的系數識別問題，陳述如下：

問題考慮如下橢圓型方程系數識別問題

(1)

u=0,在?Ω上.

(2)

其中:Ω是d,d≥1中具有Lipschitz邊界?Ω的開有界連通域，已知f∈L2(Ω)，c是未知系數，通過u在Ω上的觀測值來反演c.利用能量泛函和Tikhonov正則化方法，可獲得正則化解的收斂速度.構造如下泛函

(3)

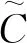
其中：ρ>0是正則化參數；c*是c的先驗估計.

1 問題設置

在本節中，主要證明了問題(1)～(2)存在唯一的解，給出解的估計，并提出了相應的反問題.

(4)

A2={a∈(L∞(Ω))n|0<|a|≤a1},

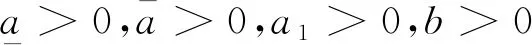
(5)

(6)

其中:

(7)

(8)

2 Tikhonov正則化

(9)

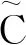
(10)

由于問題是不適定的，使用Tikhonov正則化方法求解它.即求解最優化問題

其中：ρ>0是正則化參數；c*是問題真實系數的先驗估計.

下面將介紹c*為最小范數解的概念，并概述了U(c)的一些性質.

引理1集合

在L2(Ω)-范數下是非空凸的，有界閉集.因此問題

有唯一解cz，它被稱為識別問題的c*是最小范數解.

對于此引理的證明，可參考文獻[17].

(11)

(12)

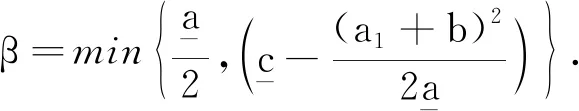
(13)

其中α>0.對任意的h∈L∞(Ω)，由Lax-Milgram引理，得到變分等式

(14)

‖η‖H1(Ω),

又因為

所以

‖h‖L∞(Ω)‖U(c)‖H1(Ω)‖η‖H1(Ω).

因此，

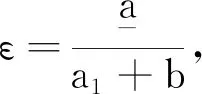
‖U(c)‖H1(Ω)‖η‖H1(Ω).

根據上一個不等式和式(6)，得下面不等式

(15)

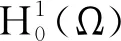
由式(14)η的定義，得到

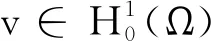
令v=U(c+h)-U(c)-η，由上式可得

所以

因此

‖η‖H1(Ω)‖U(c+h)-U(c)-η‖H1(Ω).

‖η‖H1(Ω)‖U(c+h)-U(c)-η‖H1(Ω).

根據上一個不等式和式(15)即得

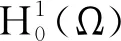
引理證明完畢.

注1由于泛函Gzδ(c)的二階Fréchet導數的部分項

(c)h2·(U(c)-zδ),

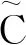
對于此定理的證明，可參考文獻[17].

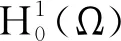
對于此定理的證明，可參考文獻[17].

3 收斂速度

因為L∞(Ω)=L1(Ω)*?L∞(Ω)*，對任意的c∈L∞(Ω)，有c∈L∞(Ω)*.于是對任意h∈L∞(Ω)有

(16)

和

‖c‖(L∞(Ω))*≤mes(Ω)‖c‖L∞(Ω).

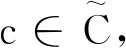
是連續線性算子(見引理2).則U′(c)的對偶算子為

因此對任意的w*∈H-1(Ω)和h∈L∞(Ω)有

(17)

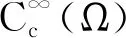
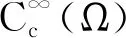
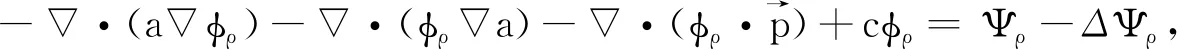
(18)

φρ=0,在?Ω上.

(19)

在H1(Ω)中的唯一解族.則存在一個常數M>0，使得對任意ρ∈(0,1)有

(20)

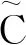
又因為

所以

使用分部積分公式和Cauchy-Schwarz不等式得

于是

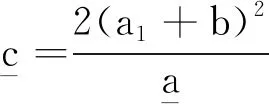
(21)

根據假設條件，存在一個常數M1>0，使得對任意的ρ∈(0,1)有

由上式和不等式(21)，對任意的ρ∈(0,1)有

(22)

根據式(22)和Poincaré-Friedichs不等式，有式(20)成立.

引理證明完畢.

定理3假設存在函數w*∈H-1(Ω)使得

cz-c*=U′(cz)*w*.

(23)

則當ρ→0,ρ～δ時，

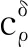
于是

(24)

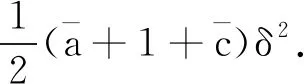
(25)

對不等式(24)右邊的第二項，根據等式(16)和(23)有

(26)

根據式(25)和式(17)可得

(27)

(28)

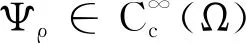
(29)

考慮下列橢圓方程Dirichlet問題

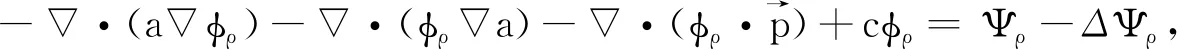
(30)

φρ=0,在?Ω上.

(31)

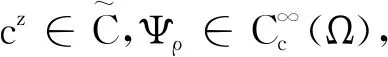
由分部積分得

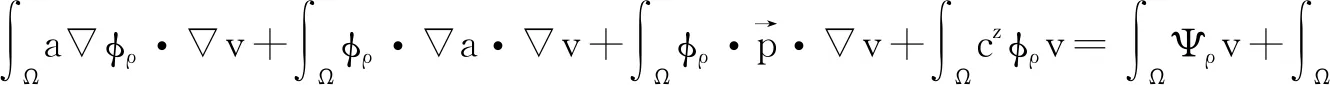
(32)

(33)

由式(27)～(28)和(33)可得

(34)

根據不等式(29)～(34)得到

(35)

(36)

根據式(4)和(11)得

根據不等式(9)得到

(37)

由不等式(29)知，{φρ}ρ∈(0,1)在H1(Ω)-范數是有界的.因此由引理4知，存在一個只依賴于Ω的常數M>0，使得對任意ρ∈(0,1)有

(38)

根據式(38)和式(35)可得

(39)

聯立(35)～(39)推出

(40)

(41)

根據不等式(24)，(25)和(40)和(41)可得，當ρ→0,ρ～δ時

即

定理證明完畢.