基于多品種流網絡的高鐵站站改前后多態理論通過能力對比分析

鮑立群,寇瑋華,闞劍鋒,許 磊,何宏暉,范 軍

(1.中國鐵路廣州局集團有限公司，廣州 510088；2. 西南交通大學 交通運輸與物流學院，成都 611756；3. 西南交通大學 綜合交通運輸智能化國家地方聯合工程實驗室，成都 611756；4. 西南交通大學 綜合交通大數據應用技術國家工程實驗室，成都 611756；5. 中鐵四局集團公司第五工程公司，江西 九江 332000；6. 中國鐵路廣州局集團有限公司調度所(施工辦)，廣州 510088)

針對車站通過能力的研究，主流思路是分別計算咽喉通過能力和到發線通過能力，核定出高鐵站通過能力，為解決偏差問題，再用通過能力評估和能力利用率等方法進行修正，但割裂了咽喉與到發線、咽喉與咽喉之間互相關聯和互相制約的關系.有些研究將車站通過能力劃分層次并對車站通過能力的影響因素進行分析，提出不同層次車站通過能力的計算方法；有些研究根據車站咽喉布局建立到發線運用關系以及按照不同技術作業參數，得出交叉進路條件下接發列車的最優化作業時序，最后提出能力損耗率的概念和計算方法；有的研究為了使綜合分析法的計算結果精確化，將一些關鍵參數取值細致化、標準化；有的研究基于高速鐵路車站咽喉區和到發線的相互制約關系，以及車站接發各種類型列車的作業過程與列車進路的關系，結合道岔分組的方法，建立咽喉區和到發線一體化運用的列車進路分配方案優化模型；有些研究盡管將站通過能力分為理論能力、實際和有效能力、可用能力等，但沒有把動車組列車對到發線占用時間的差別等因素進行綜合考慮[1-5].

盡管針對車站通過能力的研究成果很多，一直沒有形成統一的計算方法和更符合現場實際運用的推算模式.在借鑒其他專家學者研究成果基礎上，按照高鐵站基本布局將站場圖抽象為站場網絡圖，依據動車組列車車流特點，從多品種流網絡角度，按照動車組列車車流進出到發線通過咽喉區的不同順序狀態，形成符合行車規則的多態理論通過能力推算模式，利用該推算模式可以針對車站站改前后的通過能力進行縱向橫向對比，并分析出車站通過能力變化情況[6-15].

1 符合高鐵站站場布局和車流特點的多品種流網絡圖構建

1.1 多品種流網絡結構構建及生成進路數據集

將站場網絡圖咽喉區分別稱為A咽喉區和B咽喉區.設xi、yi分別表示站場圖A、B咽喉區進出車站分界點，形成點集X={…,xi,…}及Y={…,yi,…}.設定車站有m條到發線，針對到發線與A、B咽喉區的分界點形成點集A={…,Ai,…}及B={…,Bi,…}.設定vi表示咽喉區道岔，將進出站信號機也視為道岔組，即進出站信號機與進出站方向最外側道岔之間視為咽喉.針對分界點Ai和Bi分別做作A截面和B截面，到發線區域作一個流匯集的C截面.

將站場圖抽象成站場網絡圖后，在遵從行車組織基礎上，基于站場網絡圖中點線坐標的銜接關系以及行車進路生成規則，構建生成進路數據集Lpass算法，進路數據集構成如表1所列.

表1 進路數據集

為了選擇占用咽喉資源盡可能少的進路，將進路數據集中每一個起點至終點之間的進路，按照進路咽喉數量Kj遞增排序，再將每條進站進路中的咽喉按照進站順序排列，每條出站進路中的咽喉按照出站順序排列.

1.2 站場網絡圖參數構建

給定時間周期H，默認為24 h，轉換為分鐘單位周期T=60×H.根據列車運行圖、車站股道運用圖、高速鐵路行車組織細則以及能力查定報告等，查定進路準備時間Δt1、行車間隔Δt2及到發線最大停車間隔時間Δt3.

1.2.1 咽喉區域網絡參數構建

針對動車組列車咽喉占用時間主要由進路準備時間、列車通過咽喉時間以及行車時間間隔決定，這三類時間對于通過咽喉區的所有動車組列車沒有過大差異，由此可以將每列動車組列車占用咽喉時間簡化為相等.根據車站站場工程圖紙以及信號設備平面布置圖，查定每個咽喉距離，再依據文獻[16]查定動車組列車進出站速度，計算動車組列車通過咽喉時間；根據查定的Δt1及Δt2得出咽喉時間占用.取T/tij的整數作為時間周期H內咽喉通過的最大列車數即邊的容量，即有公式(1)，同時將以上參數如表2所列，其中如果Δt1<Δt2則Δt=Δt2，否則Δt=Δt1+Δt2.

cij=INT(T/tij).

(1)

基于以上分析，設定咽喉區域網絡中邊的容量、流量、時間占用為單品種流參數，咽喉區域網絡的邊如圖1所示，其中fij為邊(vi,vj)的流量，有0≤fij≤cij.

圖1 咽喉區域單品種流參數

1.2.2 到發線區域網絡參數構建

鑒于高鐵站動車組列車通過咽喉過程以及到發線停留時間的不同，對動車組列車類別歸類如表3所列.再根據列車運行圖以及車站股道運用圖查定到發線停留時間，得出到發線時間占用，將這些參數如表3所列，其中到發線時間占用中的Δt取值按照現場規則取定，即如果Δt1<Δt3，Δt=Δt3，否則Δt=Δt1+Δt3.

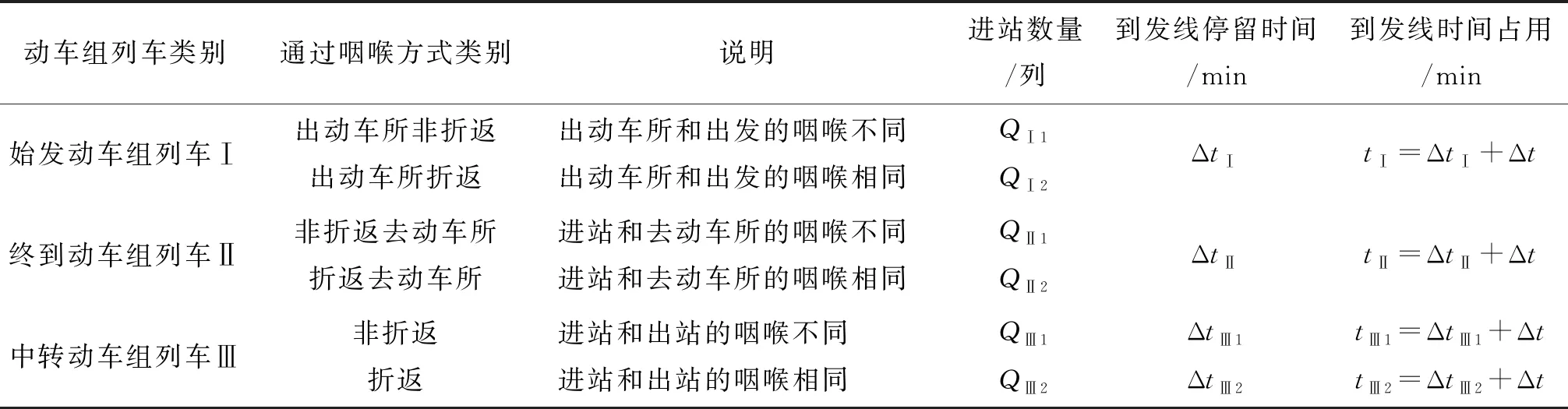
表3 動車組列車運行方式歸類及相關參數

為了表述方便，本文將表3中通過咽喉方式類別稱為6類動車組列車，即網絡圖有6種品種流.

1) 單條到發線參數確定

針對到發線節點Ai和節點Bi之間的線路，設定fⅠ1、fⅠ2、fⅡ1、fⅡ2、fⅢ1、fⅢ2分別表示6類動車組列車數量，cij表示該到發線最大能力，在時間周期T內可有fⅠ1×tI+fⅠ2×tI+fⅡ1×tⅡ+fⅡ2×tⅡ+fⅢ1×tⅢ1+fⅢ2×tⅢ2≤T以及fⅠ1+fⅠ2+fⅡ1+fⅡ2+fⅢ1+fⅢ2≤cij.由于查定的時間占用為最低限，實際行車組織中這些時間會高于查定的時間占用，另外，防止6類動車組列車在能力組合時發生數值“溢出”，采用6類動車組列車的最大到發線時間占用做為計算基準即有公式(2).

tAB=max{tⅠ,tⅡ,tⅢ1,tⅢ2},

(2)

時間周期T內單條到發線接收列車能力cAB取T/tAB的整數，即有公式(3).

cAB=INT(T/tAB).

(3)

基于以上分析，針對網絡節點Ai和Bi之間對應的到發線設定邊的參數為復合參數，其中三組參數依次表示到發線能力、6類動車組列車量及對應的時間占用，取值均為正整數或0，如圖2所示.

圖2 到發線區域多品種流復合參數

2) 所有到發線參數確定

本研究不涉及單條到發線行車方案，即不考慮公式fⅠ1×tⅠ+fⅠ2×tⅠ+fⅡ1×tⅡ+fⅡ2×tⅡ+fⅢ1×tⅢ1+fⅢ2×tⅢ2≤T中6類動車組列車數量.在遵從咽喉與到發線、咽喉與咽喉之間互相關聯和制約關系以及行車進路生成規則基礎上，基于公式(1)確定的咽喉能力以及公式(2)確定的單條到發線能力限制，確定最多能有多少動車組列車進出所有到發線，所以可以從A截面、B截面、C截面的角度研究車站理論通過能力問題.

A截面接收的最大流量有公式(4)：

(4)

式中：f(Ai)表示第i條到發線節點Ai接收的最大流量；QA表示A截面接收的最大流量.

B截面接收的最大流量QB則有公式(5)：

(5)

式中：f(Bi)表示第i條到發線節點Bi接收的最大流量；QB表示B截面接收的最大流量.

針對整個到發線C截面接收的最大流量QC則有公式(6)：

QC=QA+QB.

(6)

由此可知QC即為高鐵樞紐車站的理論通過能力，結合表3歸類的6類動車組列車可有公式(7)：

QⅠ1+QⅠ2+QⅡ1+QⅡ2+QⅢ1+QⅢ2=QC.

(7)

鑒于網絡圖流預推是在不考慮流分布狀態下，基于網絡流理論推算網絡圖能夠通過的最大流是多少即確定網絡圖能力，由此本文采用流預推方法推算公式(4)及公式(5)的f(Ai)和f(Bi)值.

2 網絡圖最大流推算的流預推過程

列車進出到發線通過咽喉區的順序不同，將會導致咽喉以及車站的通過能力結果不盡相同.盡管通過咽喉區順序不同，但必須保證“有進才有出，有出必有進”的行車原則、進入到發線進路流量、到發線剩余能力及流出到發線進路流量三者之間平衡的原則、交叉進路中共用咽喉進出流量“相互制衡”的原則.8種進出到發線咽喉先后順序的不同狀態如表4所列.

表4 進出到發線的咽喉先后順序狀態

2.1 參數查定及初始化過程

1) 根據第1.2節咽喉區域網絡參數的約定，查定距離參數和時間參數，計算通過咽喉時間Δtij，再利用公式(1)計算咽喉區域邊的容量cij值，設定流量初始值fij=0，形成表2內容的數據集.

2) 根據第1.2節到發線區域網絡參數的約定，查定6類動車組列車的時間參數并計算出到發線時間占用，形成表3內容的數據集.利用公式(2)選取計算基準，利用公式(3)計算單條到發線接收列車數最大能力cAB值，再針對到發線設定c[i]=cAB，流量初始值f[i]=0，其中i=1,…,m.

3) 設定流進入到發線進路的流量調整量為lc，流出到發線進路的流量調整量為lg.如果流進入到發線進路與流出到發線進路為交叉進路，設定lp為交叉進路中所有共用咽喉的最小剩余能力.再設定流進入到發線進路與流出到發線進路的最終調整量為lq.

4) 設定通過A咽喉流入A截面的流量總量為QA，其中通過A咽喉流出到發線的量為QAA，通過B咽喉流出到發線的量為QAB.設定通過B咽喉流入B截面的流量總量為QB，其中通過A咽喉流出到發線的量為QBA，通過B咽喉流出到發線的量為QBB.通過A咽喉流入A截面但無法流出的量為QAD，通過B咽喉流入B截面但無法流出的量為QBD.

2.2 流量預推過程

盡管行車中涉及到進路之間交叉以及敵對進路等現象，但在能力計算上均體現為“能力消耗”，另外，流預推時流入到發線的流同時又從同一個咽喉區流出，會出現“能力對沖”問題，所以算法中需要建立 “能力消耗”以及“能力對沖”相對應的推算公式.鑒于表4每種狀態的流預推過程相同，本文以“A咽喉優先進到發線”的“A咽喉進A咽喉出B咽喉出+ B咽喉進A咽喉出B咽喉出”為例說明流預推算法過程.

算法2.1“A咽喉進A咽喉出B咽喉出” 流預推算法

1) 如果A咽喉存在還沒有被選定過的進站方向點xi，選定該點作為進站進路起點，否則轉到“B咽喉進A咽喉出B咽喉出”的子過程.

2) 如果存在c[i]-f[i]>0的到發線，選定Ai作為進站進路終點，否則轉到第(1)步.

3) 按照行車進路規則，推斷xi和Ai之間的進站進路，如果不存在進路，轉到第(2)步.

4) 根據第(3)步推斷的進站進路，針對該進路中所有邊選擇lc=min{…,cij-fij,…}.如果lc=0，轉到第(2)步，否則使lq=min{lc,c[i]-f[i]}.

5) 如果A咽喉存在還沒有被選定過的出站方向點xi，選定該點作為出站進路終點，否則轉到第(11)步.

6) 按照行車進路規則，推斷Ai和xi之間的出站進路，如果不存在進路，轉到第(5)步.

7) 根據第(6)步推斷的出站進路，針對該進路中所有邊選擇lg=min{…,cij-fij,…}，如果lg=0，轉到第(5)步.

8) 根據第(3)步推斷的進站進路和第(6)步推斷的出站進路，判定兩個進路是否為交叉進路.如果不是交叉進路，使lq=min{lq,lg}；如果是交叉進路，針對兩條進路中所有的共用咽喉選取最小的剩余能力lp=min{…,cij-fij,…}，使lq=min{lq,INT(lp/2)}.

9) 針對進站進路、出站進路中所有咽喉以及第i個到發線進行流量調整，即所有咽喉流量調整為fij=fij+lq和第i個到發線流量調整為f[i]=f[i]+lq.通過A咽喉流入A截面流量總量QA=QA+lq，其中通過A咽喉流出到發線的量QAA=QAA+lq.

10) 如果存在lc-lq>0，轉到第(5)步，否則轉到第(1)步.

11) 如果B咽喉存在還沒有被選定過的出站方向點yi，選定該點作為出站進路終點，否則轉到第(1)步.

12) 按照行車進路生成規則，推斷Ai和yi之間的出站進路，如果不存在進路轉到第(11)步.

13) 根據第(12)步推斷的出站進路，針對該進路中所有邊選擇lg=min{…,cij-fij,…}，如果lg=0，轉到第(11)步，否則使lq=min{lq,lg}.

14) 針對進站進路、出站進路中所有咽喉以及第i個到發線進行流量調整，即所有咽喉流量調整為fij=fij+lq和第i個到發線流量調整為f[i]=f[i]+lq.通過A咽喉流入A截面流量總量QA=QA+lq，其中通過B咽喉流出到發線的量QAB=QAB+lq.

15) 如果仍然存在lc-lq>0，轉到第(11)步，否則轉到第(1)步.

算法2.2“B咽喉進A咽喉出B咽喉出” 流預推算法

該過程和上一過程思路相同，鑒于篇幅所限不再贅述.最后同樣得出通過B咽喉流入B截面流量總量QB，其中通過A咽喉流出到發線的量QBA，通過B咽喉流出到發線的量QBB.

利用兩個算法進行流預推有可能出現剩余進站能力，即通過上一過程推算后，存在通過進站進路可以流入到發線但無法流出的能力.推斷進路以及確定進路流量的思路和上一過程相同，差別是不再尋找出站進路，最后可以得出通過A咽喉只能流入A截面的量QAD，通過B咽喉只能流入B截面的量QBD.

鑒于本文研究內容的人工計算量大以及計算過程復雜等原因，基于研究思路和研究方法開發了《高鐵站通過能力計算及行車組織優化系統》，利用該系統進行推算、計算數據的同時，也可以驗證本文研究思路和研究方法是否具有可行性.

3 深圳北站站改前后理論通過能力推算分析

深圳北站是具有一定規模的高鐵樞紐站，有m=20條到發線和具有動A線和動B線的1個動車所，北咽喉有廣州方向，南咽喉有廈門和香港方向，針對深圳北站站場圖構建A截面、B截面、C截面，站改前站場圖抽象成站場網絡圖的示意圖如圖3所示.

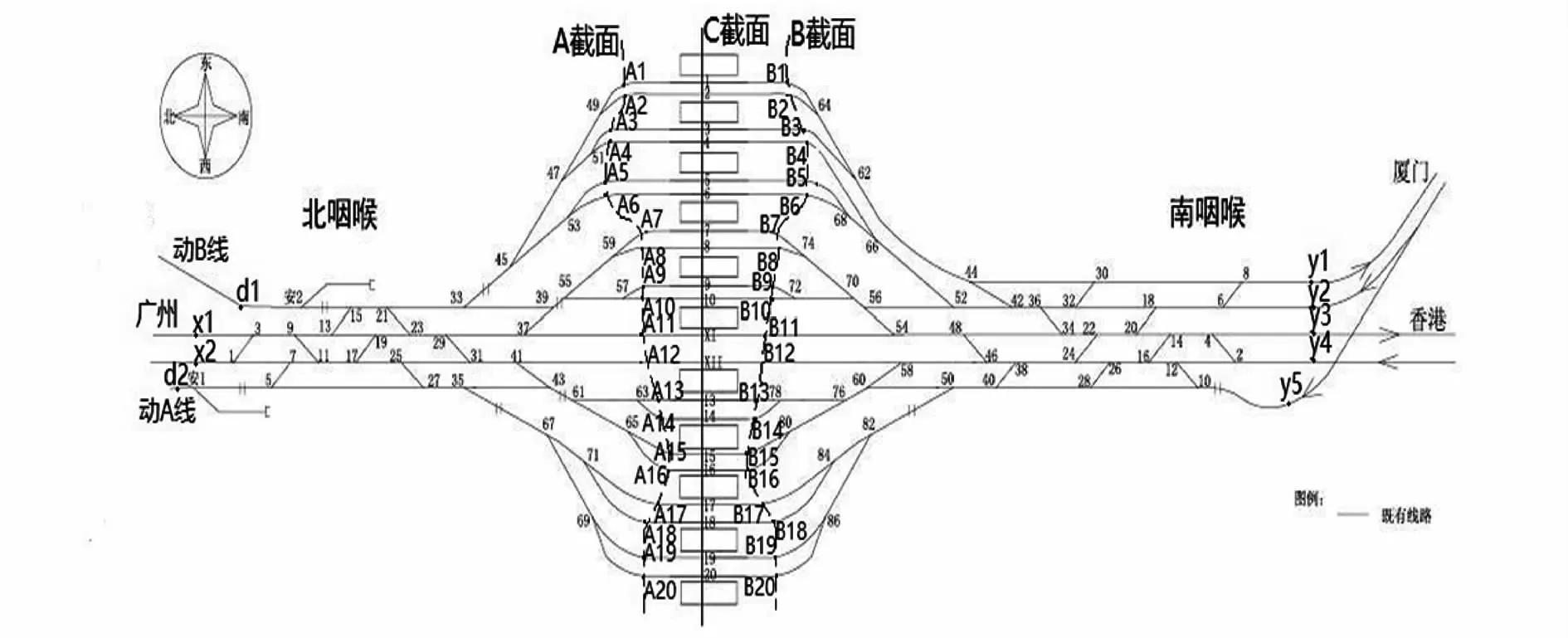
圖3 構建A、B、C截面的深圳北站站改前站場圖

3.1 時間占用參數確定及咽喉能力推算

將天窗時間以及深圳北站運行圖的最早最晚接發車時間結合起來綜合考慮，這里取H=18 h，即有T=60×18=1 080 min.為了提高接發能力，深圳北站于2019年11月開始進行贛深方向新線引入以及第二動車所的建設.以站改后站場圖抽象為網絡圖為例的咽喉能力計算結果如圖4所示.

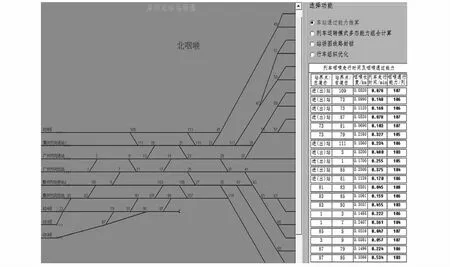
圖4 深圳北站站改后站場網絡圖及咽喉能力

查定規定進出站車速v=40 km/h及每個咽喉距離lij，得出動車組列車的行駛時間Δtij=l/v×60 min.查定的進路準備時間Δt1=5 min、列車行車間隔Δt2=5 min、到發線停車間隔Δt3=8 min，可以得出數據集如表5所列.

表5 深圳北站動車到發線時間占用參數

3.2 深圳北站理論通過能力推算

利用《高鐵站通過能力計算及行車組織優化系統》中基于本文研究思路和方法形成的功能，針對深圳北站站改前及站改后分別推算出表4所示8種多態理論通過能力，多態理論通過能力結果分別如圖5～6所示，分布狀態分別如圖7～8所示.對比可以看出數據分布非“極端”的才符合行車組織可行情況.另外，站改前后通過能力數據分布合理與否，二者之間的同一種狀態都互相對應.

圖5 站改前多態理論通過能力推算結果

圖6 站改后多態理論通過能力推算結果

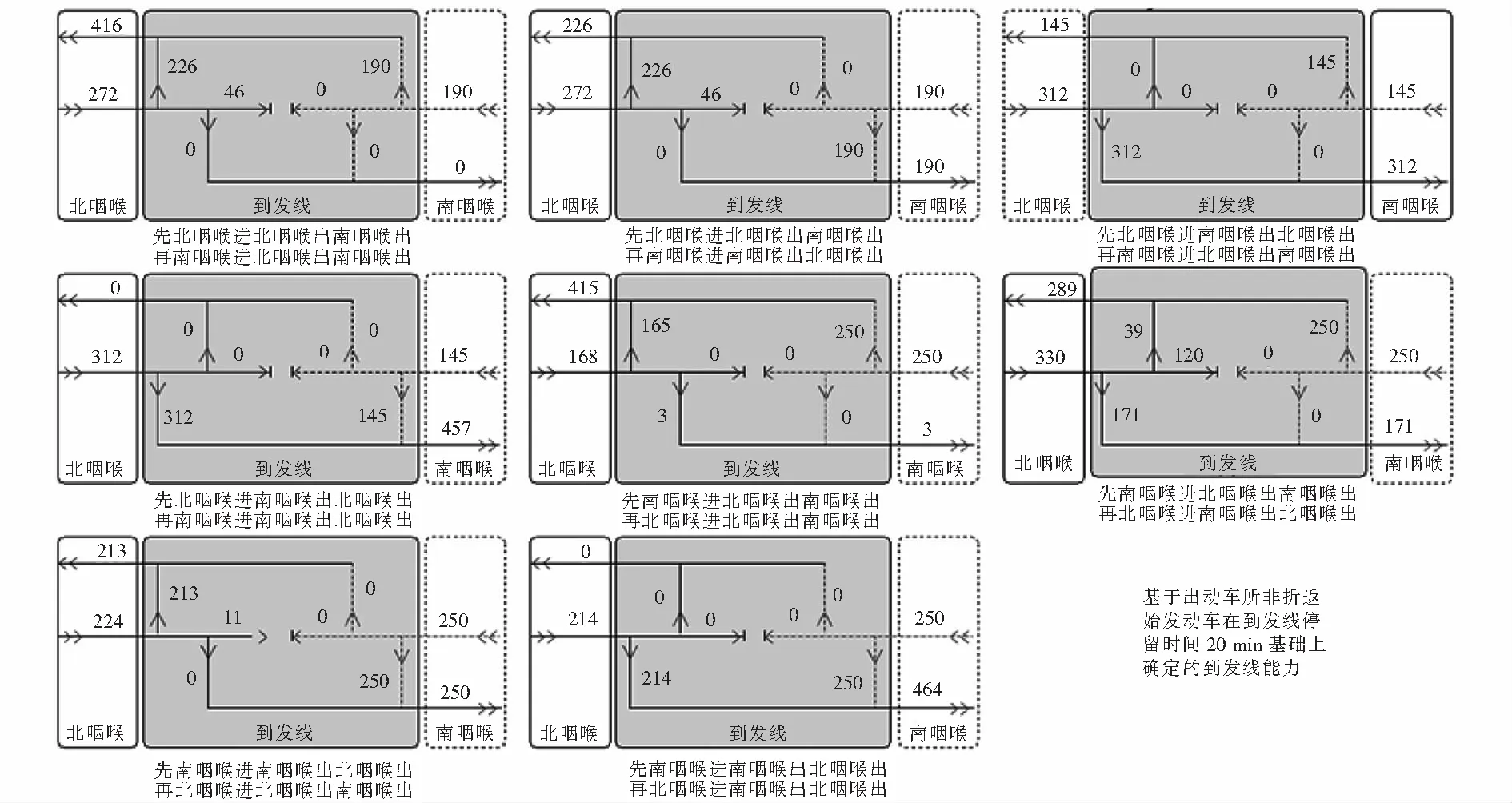
圖7 深圳北站站改前多態理論通過能力分布狀態(單位:列)

3.3 深圳北站站改期間通過能力影響分析

深圳北站站改主要對站場北咽喉進行，南咽喉的站場布局與站改前大致相同，所以車站站改通過能力變化主要由北咽喉引起.北咽喉站改后原有廣州方向行車線不變，增加贛州方向三條行車線，同時增加深圳第二動車所，這將導致北咽喉通過能力增加，也必然會導致車站通過能力增加，由于咽喉區與咽喉區之間通行能力的互相關聯和互相制約關系，也會導致南咽喉通過能力發生變化.

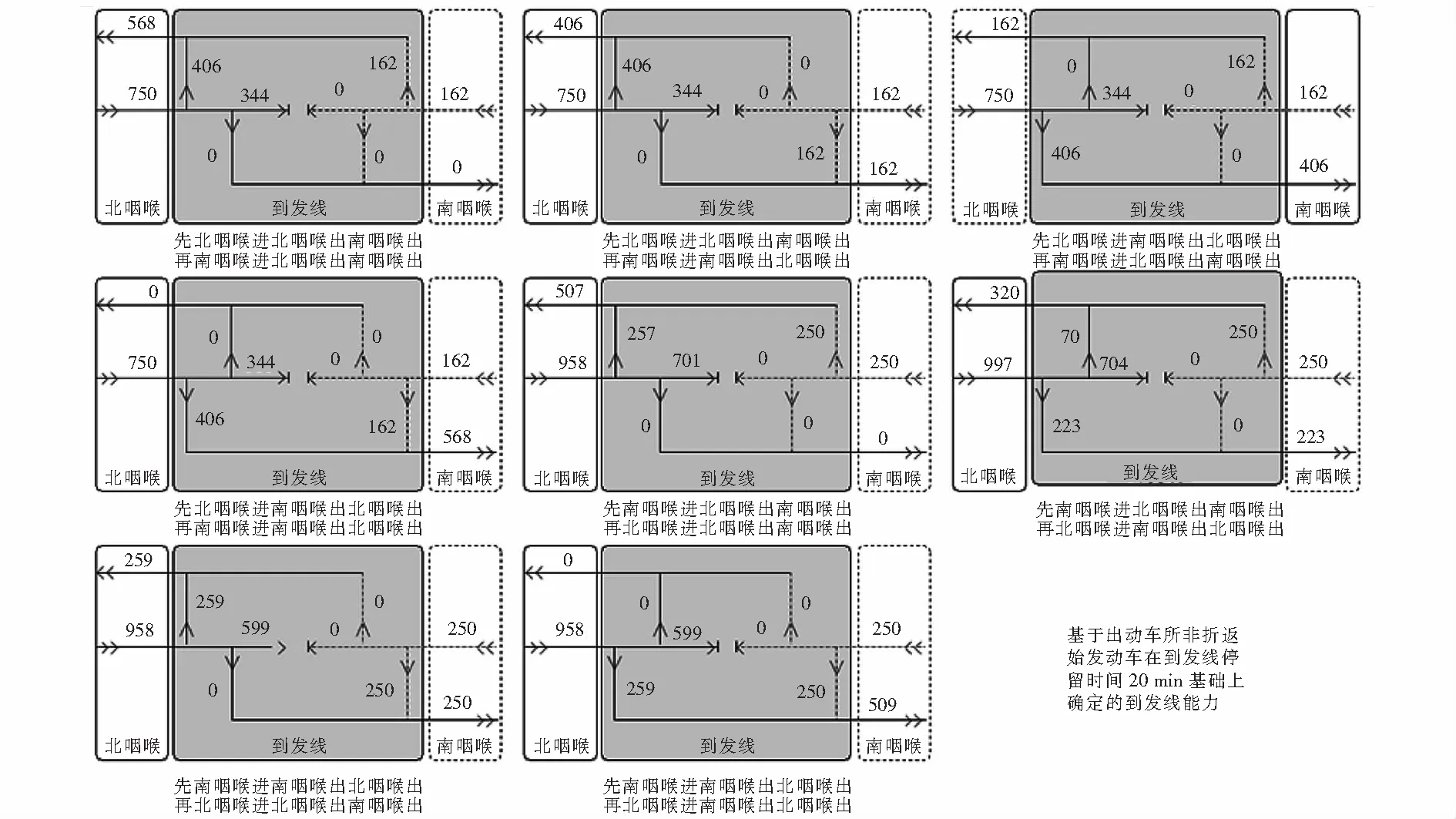
圖8 深圳北站站改后多態理論通過能力分布狀態(單位:列)

咽喉進站能力和出站能力的大小決定了咽喉和車站通過能力的大小，但數據 “極端分布”和“極端不均衡”狀態不屬于車站行車常態，本文根據圖5～8選取4種數據分布“非極端相對均衡”的狀態進行站改前后通過能力對比分析，將4種狀態分別記作A、B、C、D狀態，如表6所列.

表6 深圳北站站改前后通過能力對比

針對以上4種可行狀態的通過能力分析總結如下：

1) 站改前每種狀態的車站通過能力受限于咽喉通過能力，但站改后每種狀態的車站通過能力受限于到發線接發能力，這也為未來車站通過能力的擴展提供了方向.

2) 站改前每種狀態的車站通過能力變動幅度比較小，站改后有2種狀態的咽喉通過能力變動幅度較大，其余兩種狀態的咽喉通過能力變化幅度較小.

3) 站改前車站通過能力最低為416對，最高為463對，范圍相差463-416=47對，但有3種狀態的通過能力都集中在460對附近，可以推斷深圳北站站改前通過能力約為460對.

4) 站改后車站通過能力分兩種情況，北咽喉區優先順序時，有兩種狀態為568對，結果相同，可以推斷通過能力大約為568對；南咽喉區優先順序時，通過能力最高為543對，最低為509對.

5) 針對同一種狀態下，站改后北咽喉通過能力的變化量以及變化程度，較站改前的差異變化較大，南咽喉變化較小.

6) 站改后北咽喉區優先順序時，咽喉通過能力和車站通過能力增加幅度都在24%以上，甚至A狀態下達到了79%；南咽喉區優先順序時，車站通過能力增幅保持在20%以下.

7) 站改后的A狀態下，南咽喉的通過能力沒有增加反而減小，是因為受到發線能力的影響，北咽喉站改后通過能力大幅度增加，由北咽喉優先進入占用了較多到發線資源，從而使得南咽喉的通過能力減小.

4 結論

利用多品種流網絡理論首創性地研究了車站站改前后通過能力對比分析，為相關研究提供了一種全新的研究視角，可以為站改方案評估以及行車組織優化等提供可靠實用的依據和決策上的支撐，也可以針對不同的站改方案，比選出可行、滿意的方案.