基于Fischer算法的地鐵公用通信系統比特功率分配研究

程 璇，高云波，李茂青，王國榮，馬 瑞

(蘭州交通大學 自動化與電氣工程學院，蘭州 730070)

城市軌道交通系統根據軌道建筑物所處的空間位置、運行方式、運量大小、軌道結構、管理方式的不同，劃分為地下鐵道、單軌交通、有軌電車、小型地鐵以及軌道新交系統.由于地下鐵道輸送能力大，運營干擾小，且舊城區一般各種建筑物、結構物密集，市政道路多，干擾大，改建難度十分大，因此，我國大部分城市的軌道交通系統建設基本上選擇地下鐵道，簡稱地鐵.

地鐵作為城市軌道交通系統的一種主要方式，以其運量大、速度快、安全性高、價格低等優勢在城市交通網中發揮著重大作用，為民眾日常出行帶來極大便捷.而地鐵中為普通民眾提供服務的公用無線通信系統，主要通過引入運營商地面基站的信號實現覆蓋，其與蜂窩通信均屬于無線通信，區別在于地鐵采用敷設漏纜的方式引入信號.

目前，在中國移動5G的部分頻段、中國聯通LTE及中國電信LTE的部分頻段中，均采用了正交頻分復用(orthogonal frequency division multiplexing,OFDM)技術來區分多個不同的用戶，它是一種多載波技術及一種調制方式[1-2]，通過將寬帶信道在頻域上分成若干個正交的子信道來提高頻譜利用率.對于地鐵公用通信系統中的部分用戶，正是通過頻分雙工(frequency division duplexing,FDD)模式來通信的.傳統OFDM技術采用固定調制的方式來分配比特及功率資源，存在著數據誤比特率(bit error ratio,BER)較高的問題，而自適應策略能根據系統的實時信道狀態信息(channel state information,CSI)相應地調整傳輸策略以匹配當前的信道狀態[3].

目前，功率分配算法分為兩類：第一類是多用戶之間的資源競爭與協調.文獻[4]利用線性注水算法，對無線紫外線非直視MIMO通信系統進行功率分配，提升了系統容量；文獻[5]構建了具有線性約束的非線性優化模型，證明了其最優解滿足比例公平性及最大-最小公正性，為電動汽車充電站提供了一種實時最優的功率分配；文獻[6]針對高速鐵路環境，以滿足用戶服務質量需求且兼顧信道的公平性為優化目標，研究了基站固定功率約束下的功率分配問題.第二類是單用戶在多子載波之間的資源分配.在理論上屬于最佳分配的線性注水算法優化[7]，其運算復雜度較高，且在進行比特分配的時候不一定得到確定的整數，導致比特分配為分數時子載波將很難進行調制，使得注水算法在實際應用中十分困難.但研究人員基于該思想陸續提出了很多單用戶的自適應比特及功率分配方案，如Hughes-Hartogs算法[8]、Chow算法[9]、Fischer算法[10]及一些改進算法.

綜上所述，目前暫無針對地鐵公用無線通信系統的功率分配研究，且在地鐵公用無線通信系統中，每個小區內的中國移動LTE/5G、中國電信LTE/5G、中國聯通LTE/5G等各類用戶是混合存在的，它們使用的通信頻段各不相同、互不影響.因為采用了FDD技術的用戶量有限，每個用戶不止被分配一個子載波，故研究地鐵公用無線通信系統中單用戶在其子載波集上的自適應比特及功率分配具有實際意義.

本文將立足我國的地鐵網絡架構及FDD雙工模式應用現狀，構建系統優化模型.擬從經典的單用戶多載波自適應比特及功率分配算法出發，將自適應Fischer算法應用到地鐵公用無線通信系統中，并將它們進行綜合對比分析，進一步驗證其性能.

1 系統模型及優化問題

1.1 地鐵系統模型

1.1.1 地鐵網絡架構

地鐵中漏纜的頻段覆蓋在450 MHz～2.4 GHz以上，適應現有的各種無線通信體制，具有信號覆蓋均勻、產品使用壽命長、穩定可靠、多系統總體造價低等優勢[11]，因此，在長隧道地區均采用漏纜實現公用通信系統的布設.

圖1為地鐵區間漏纜布置示意圖.信號漏纜均架設在弱電七層電纜托架上，公網漏纜1、2、3、4多由鐵塔公司敷設，從上至下分別是2G、3G、4G、5G網絡，位置正對列車車窗，確保接收信號較好.整個公用通信系統下行通信鏈路包含了有線和無線部分.有線鏈路部分為：運營商基站-傳輸設備-室內基帶處理單元(building base band unit,BBU)-遠端射頻模塊(remote radio unit,RRU)-漏纜；無線鏈路部分為：漏纜-公用用戶.本文重點研究無線通信過程中的自適應調制過程.

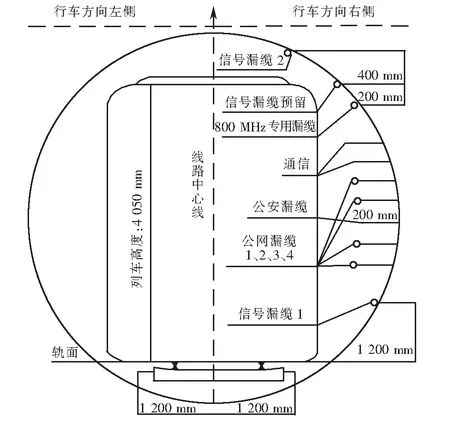
圖1 地鐵區間漏纜布置示意圖

1.1.2 公用無線通信系統FDD雙工模式頻段

表1為中國三大運營商目前采用了FDD雙工模式的頻段表.以中國電信LTE網絡為例：系統帶寬為15 MHz，則對應的資源塊(resource block,RB)為75個，在3GPP制定的協議中，子載波的間隔為15 kHz和7.5 kHz；若子載波的間隔為15 kHz，對應的子載波數為900個，此時傳輸帶寬為900×15 kHz=13.5 MHz，保護帶寬為1.5 MHz.在場景中的電信LTE用戶數有限，因此每個用戶不止分配一個子載波.

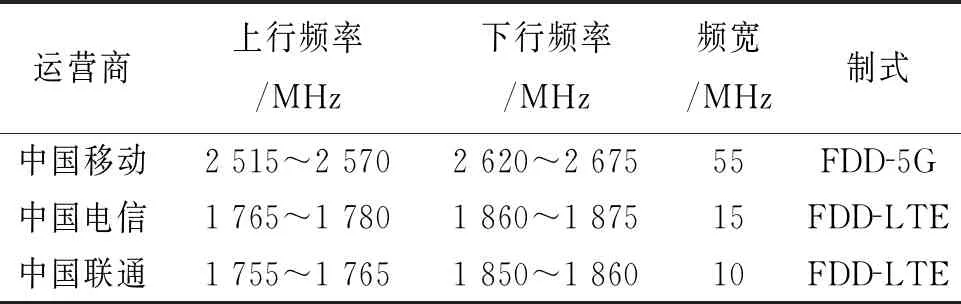
表1 FDD雙工模式頻段表

1.2 優化模型

1.2.1 自適應調制流程

在OFDM系統中，可供分配的資源有：子載波、比特及功率.當系統中有多個用戶時，首先完成子載波的分配過程，將多個子載波根據一定的規則分配到單個用戶；其次，利用算法對每個單用戶的子載波集再分配比特及功率.本文重點探討OFDM自適應調制過程，即比特及功率分配.

OFDM系統在多個子載波上采用多進制調制方式來進一步提高頻譜利用率.正交振幅調制(quad-rature amplitude modulation,QAM)作為近年來在國際上被廣泛應用的一種信號調制方式，可充分利用帶寬，抗噪聲能力強.在調制過程中，QAM是同時以載波信號的幅度、相位代表不同的數字比特編碼，把正交載波技術與多進制相結合，以進一步提高頻譜利用率.本文誤比特率的計算將基于QAM.

圖2為OFDM系統自適應調制流程.首先由發送方給接收方發送信道測量信號；接收方根據接收的信道測量信號，估計當前時隙的信道信息，并將其反饋給發送方；發送方根據信道信息選擇最適合的資源分配方式和編碼調制參數，完成調制過程并發送；接收方通過信息或盲檢測方式完成接收信號的解調，一次通信過程完成.

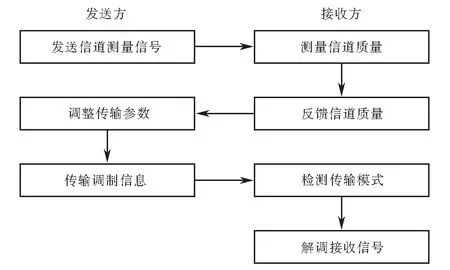
圖2 OFDM自適應調制流程

1.2.2 系統優化模型

根據優化目標的不同，OFDM自適應比特及功率分配算法分為3類[12]：1) 在總發送功率一定和滿足系統BER約束時最大化系統傳輸速率；2) 在總傳輸速率一定和滿足系統BER約束時最小化系統的發射功率；3) 在總發送功率和總傳輸速率一定時最小化系統的BER.在實際的通信過程中，往往更加關注如何用有限的功率資源達到某種速率的傳輸.考慮到城市軌道交通系統發射功率固定的特點，以及人們對無線移動業務要保證單用戶的傳輸速率的高需求，本文主要探討基于誤比特率最小準則[13]下的分配算法，其優化模型為：

minBER;

(1)

(2)

其中：RT、PT分別為總發送比特數及發射總功率；bi為第i個子載波的發送比特數；Pi為第i個子載波的發射功率；N為總的子載波數.

2 算法描述

Fischer算法是由R.F.H.Fischer和J.B.Huber在1996年提出的，由于在算法中比特的分配采用的是閉式解，Fischer算法省略了大量的排序、搜索運算操作，運算量較小，尤其當系統中子載波數非常多時優化效果更明顯，更適合在高速數據傳輸系統中使用.Fischer算法具體過程如下：

QAM的誤比特率Pr表示為

(3)

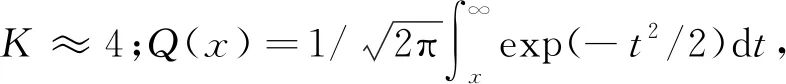
Fischer指出，系統性能受限于誤比特率最高的子信道，只有所有子載波上具有相同的誤比特率，系統才是最優的[14].記任意子載波的誤比特率為Pri，記其大小為固定值const，即

Pri=const,i=0,1,…,N-1.

(4)

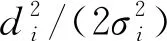
(5)

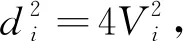
(6)

(7)

(8)

由于PT是固定值，通過拉格朗日優化可知，要使得SNR0最大，則有：

(9)

(10)

通過式(10)可以初步求得所有子載波的bi，但bi小于0則說明該子載波不可用，需進行剔除操作.記原來的N個總子載波經剔除操作后用N′表示，記此時N′個可用子載波組成的子載波集合為S′，則

(11)

根據式(11)重新計算各子載波上分配的比特數，反復迭代，直至bi均大于0，此時所有子載波上均分配了比特數.而系統總發射功率平均分配在各個子載波上，有

Pi=PT/N.

(12)

由于實際應用中調制的比特數必須為整數，則需要對bi進行量化，即:

(13)

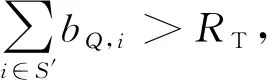
(14)

Fischer算法通過提前存儲所有子載波的對數噪聲方差值，簡化了算法復雜度，在實際運算中僅涉及加法、除數為整數的除法，經過幾次迭代就能得到最終結果，它是目前效率比較高的自適應分配算法，被用在許多系統中.同時，Fischer算法可使得系統中所有可用的子載波具有相同的誤比特率性能，進而使得系統的誤比特率降到最低，提高了數據傳輸的準確性.圖3為Fischer算法流程圖.

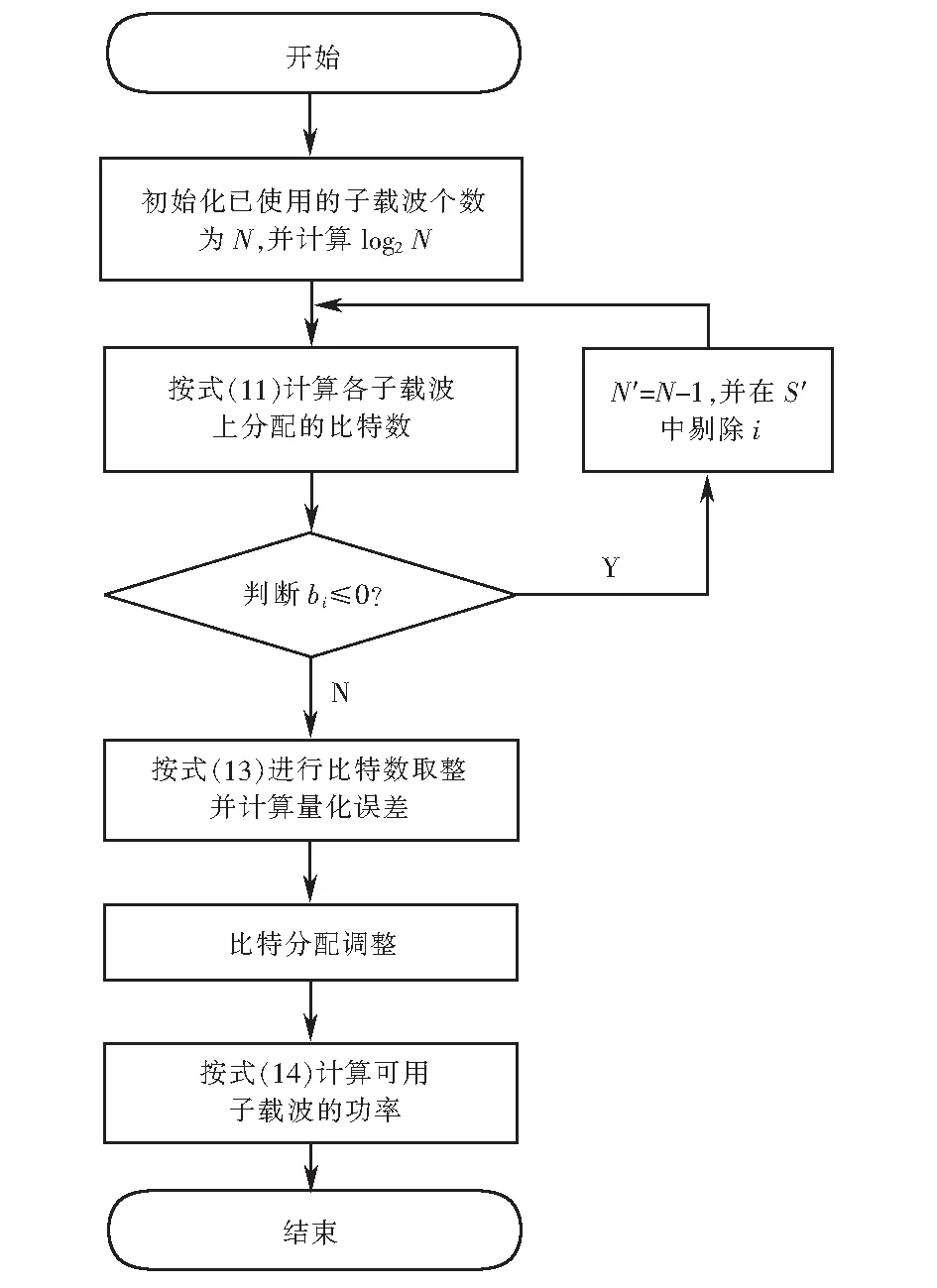
圖3 Fischer算法流程圖

3 算法復雜度分析

算法復雜度是衡量算法實時性的重要指標，表2為3種自適應算法的理論復雜度比較表[15].表2中，R為Hughes-Hartogs算法中系統傳輸比特數；MaxCount為Chow算法為保證收斂度而設置的最大迭代次數；R′為Fischer算法依據誤比特率最優解公式得到的預分配總比特數目.對表2進一步分析可看出，Hughes-Hartogs算法的復雜度隨N、R的增大而急劇增大，嚴重影響算法收斂速度，并不適用實時性要求較高的地鐵公用通信系統；Chow算法通過設置最大迭代次數在一定時間后跳出循環以保證運算收斂性，不需要大量搜索和排序，復雜度遠小于Hughes-Hartogs算法，更適用于現實系統；而Fischer算法則利用閉式解來直接分配比特信息，比前兩種算法復雜度進一步降低，更適用于高速傳輸系統.

表2 不同算法復雜度比較

4 仿真結果與分析

4.1 仿真參數設置

在地鐵隧道的無線通信信道環境中，總信號的強度服從瑞利分布，瑞利衰落能有效描述存在直射徑和非直射徑存在多障礙物的無線傳播環境.由此，本文對各子載波的信道增益采用多徑瑞利衰落信道來仿真，采用理想信道估計，對每個子載波上的平均功率進行歸一化處理.其他仿真參數設置見表3.

表3 系統仿真參數

4.2 仿真結果

1) 比特及功率分配對比

圖4～6給出了某次分配時3種自適應算法的信道增益、傳輸比特、發射功率的分配情況，可以看出：

① 3種方法均根據信道狀況進行自適應比特分配，以確保最終使用的子載波上一定有信息傳輸.在頻率選擇性衰落中，同一時間里不同子載波所經歷的衰落各不相同，部分子載波的信道衰落小、傳輸速率快，而有些子載波則存在嚴重的衰落、傳輸條件較差.

② 子載波上的傳輸比特數與信道條件正相關，對信道增益大、通信質量好的子載波上會分配更多比特數，如圖4中第2個子載波上分配的比特數大于第3個子載波；反之，信道增益小、通信質量差的子載波分配的比特數少；對于存在嚴重衰落導致信道條件極差的子載波則可能不分配比特，如圖6中第9個子載波.

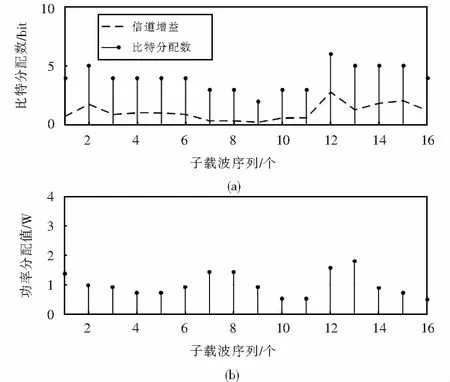
圖4 Hughes-Hartogs算法比特和功率分配

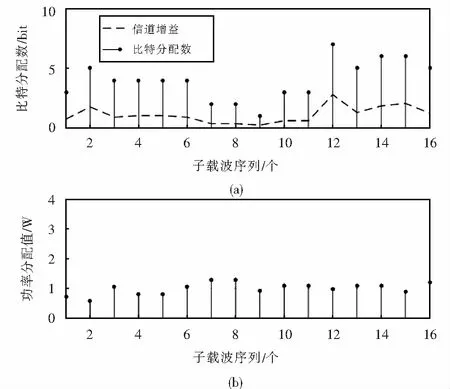
圖5 Chow算法的比特和功率分配

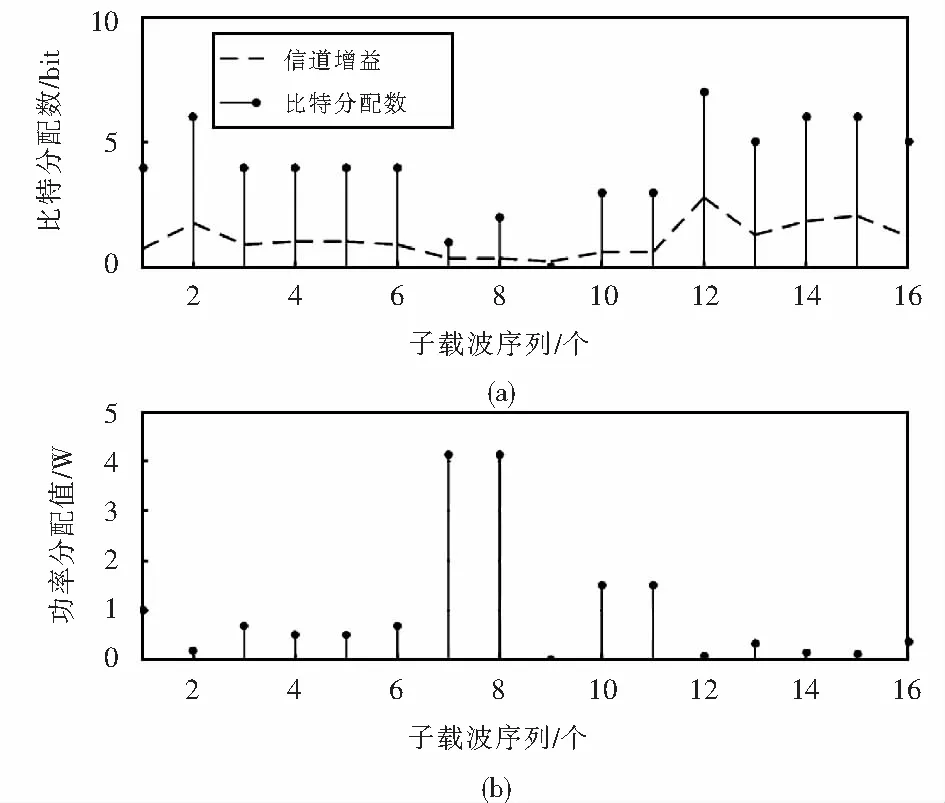
圖6 Fischer算法的比特和功率分配

③ 子載波上分配的發送功率和信道增益緊密相關.對分配比特數相同的子載波，功率分配值與信道增益的大小成反比，信道增益越大、通信質量越好，其所需的功率就越小，越節省資源，如圖5中信道增益更大的第15個子載波上所分配的功率就小于信道增益稍小的第14個子載波的.

④ Fischer算法比Hughes-Hartogs算法、Chow算法在一些子載波上的分配功率要大很多，這是由于3種算法的優化目標不同導致的.Fischer算法優化目標是使系統的BER最小，那么在信道狀況比較差的信道就會分配較多的功率，仿真結果也與該目標相一致.

總的來說，在比特分配中，Hughes-Hartogs算法、Chow算法在信道質量較差的子載波(如9號子載波)上也承擔了一部分比特的傳輸，而Fischer算法對信道質量的好壞更加敏感，直接將該信道質量過差的子載波舍棄；在功率分配過程中，Hughes-Hartogs算法、Chow算法功率的分配結果較為均衡，Fischer算法則起伏更大，比起另外兩種算法，Fischer算法在信道質量較好的子載波上僅使用很小的功率就能實現信息傳送.

2) 誤比特率性能分析

算法誤比特率性能是衡量算法可靠性的重要指標.對每個子信道信噪比下進行800次仿真取平均值，得到不同算法誤比特率隨信噪比的變化曲線，如圖7所示.從圖7中可以看出：誤比特率與系統信噪比成反比，它隨著信噪比的增大而降低，3種自適應算法的誤比特性能明顯優于傳統OFDM固定調制下的等功率分配；Chow算法誤比特性能最優，Fischer算法、Hughes-Hartogs算法誤比特性能較為接近；在誤比特率為10-4時，Fischer算法和Hughes-Hartogs算法的子信道平均信噪比要比等比特功率分配算法小約4 dB；同時從前面復雜度分析來看，Fischer算法比前兩種算法復雜度進一步降低，更適用于高速傳輸系統，證明了自適應Fischer算法的優勢和適用性.

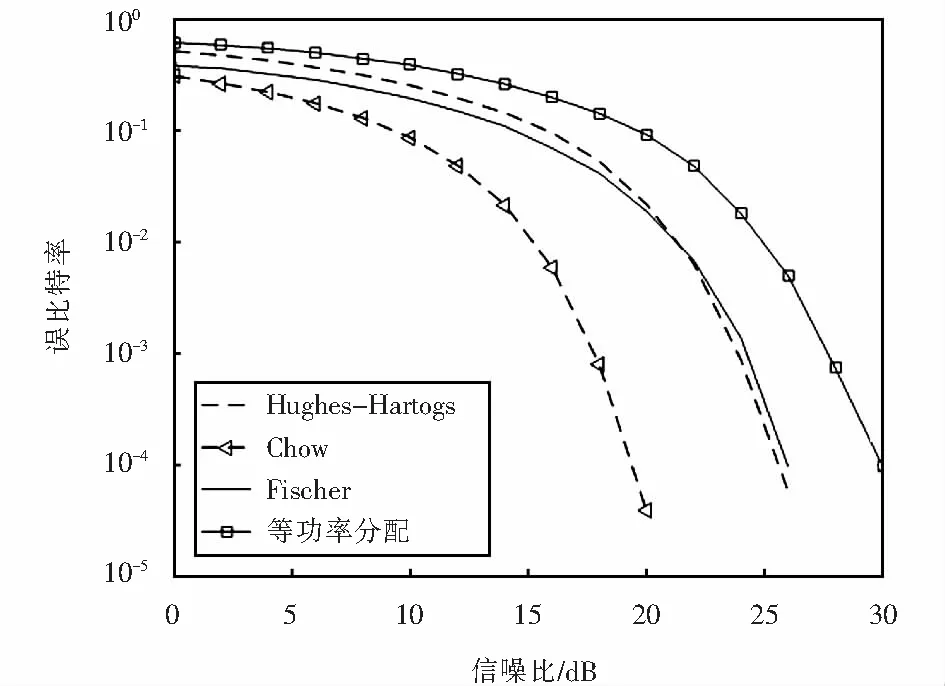
圖7 不同算法誤比特率比較

5 結論

本文在地鐵公用通信系統中引入了自適應策略來改善傳統OFDM固定調制時數據誤比特率較高的問題.采用了自適應Fischer算法來完成單用戶在子載波集上的比特及功率分配，該算法綜合考慮了功率限制約束、傳輸速率要求，兼顧實時性和誤比特率性能改善；復雜度分析表明，Fischer算法實時性更好，更適用于高速傳輸系統.仿真結果表明，Fischer算法對信道質量的好壞更加敏感，在信道質量較好的子載波上僅使用很小的功率就能實現信息傳送，且該算法能有效地改善誤比特率性能，在誤比特率為10-4時，Fischer算法的子信道平均信噪比要比等比特功率分配算法小約4 dB.