古今碰撞 邁好證明“第一步”
——以蘇科版 “三角形內角和定理”證明為例

姜鴻雁 秦語真 孫丹丹

(1.江蘇省無錫市河埒中學214062；2.華東師范大學教師教育學院200062；3.山東師范大學數學與統計學院 250358)

1 引言

“證明”是數學學科至關重要的內容，滲透到數學的枝枝蔓蔓.蘇科版教材七年級下冊第12章專講“證明”，這一章第2節“證明”分3個課時層層推進，從說明“證明”的必要性到“什么是證明”再到“證明與圖形有關的命題的一般步驟”，給出規范的“三段論”證明格式，最后1課時主要內容為“三角形內角和定理”的證明及其推論[1].

蘇科版教材第7章“平面圖形的認識(二)”中已經對三角形內角和為180°的緣由進行過說理，但在形式上并沒有以規范的“三段論”方式進行，這應該是教材編寫者基于符合學生數學學習的心理規律的角度考慮的.那么本節課教學是不是僅以內容為中心，簡單定位為將定理以三段論的形式“嚴格證明”一遍？顯然不是.三角形內角和定理位于“證明”這一章，按照教材編排思路，應以內容為載體服務于“證明”的教學，以承載更大的教育教學價值.因此，我們借助三角形內角和定理豐富的歷史素材，以思想方法為中心設計開展本課時教學.

現有的教學設計中，依托數學史進行教學設計的案例不在少數[2]～[5]，筆者認為，這些設計基本是聚焦“知其然、知其所以然”兩個層面，沒有很好地解決“知何由以知其所以然”這一方法論問題，而以具體內容為載體，助力學生對一般證明思路的洞察是本節課應該承載的價值.此外，以往課例對方法多樣性本質的提煉、育人價值的挖掘不夠充分.筆者認為，學生在探究證明方法多樣性的過程中，應該對為何證明、證明特點以及怎么開展證明等問題有更多的思考，這樣的上位認識對將來的數學學習非常重要.

2 史料介紹與分析

從古希臘七賢之首泰勒斯(Thales，公元前6世紀)發現“三角形內角和等于二直角”以來，歷時2000多年，數學家們一直探索這個結論的不同驗證及證明方法，經久不衰.就證明而言，首先是畢達哥拉斯(Pythagoras，約公元前560—480)學派證明了這個定理(如圖1)，過頂點A作邊BC的平行線，由兩直線平行，內錯角相等，實現角的轉移，結合平角證得結論[6].

之后，歐幾里得(Euclid，約公元前330—270)在《幾何原本》中給出新的證明方法(如圖2)，過頂點C作AB邊的平行線，由兩直線平行，內錯角、同位角相等，結合平角得到結論[6].

圖1 畢達哥拉斯的證明方法

圖2 歐幾里得的證明方法

在公元5世紀，古希臘評注家普羅克拉斯(Proclus，410—485)用了兩種方法證明了這個定理，經歷了從特殊到一般的過程[7].第一種證明方法如圖3所示，先是分別過A、B、C三點作BC邊的垂線，則BE∥AD∥CF，通過兩直線平行，內錯角相等轉化角，由兩直線平行，同旁內角互補證得結論.第二種證明方法，將輔助線一般化(如圖4)，在∠BAC內部任意作線段AD，分別過B、C作AD的平行線，本質與作垂線的方法一致.

18世紀法國數學家克萊羅(A. C. Clairaut，1713—1765)過點A作BC的平行線，由兩直線平行，內錯角相等、同旁內角互補證得結論(如圖5)[7].

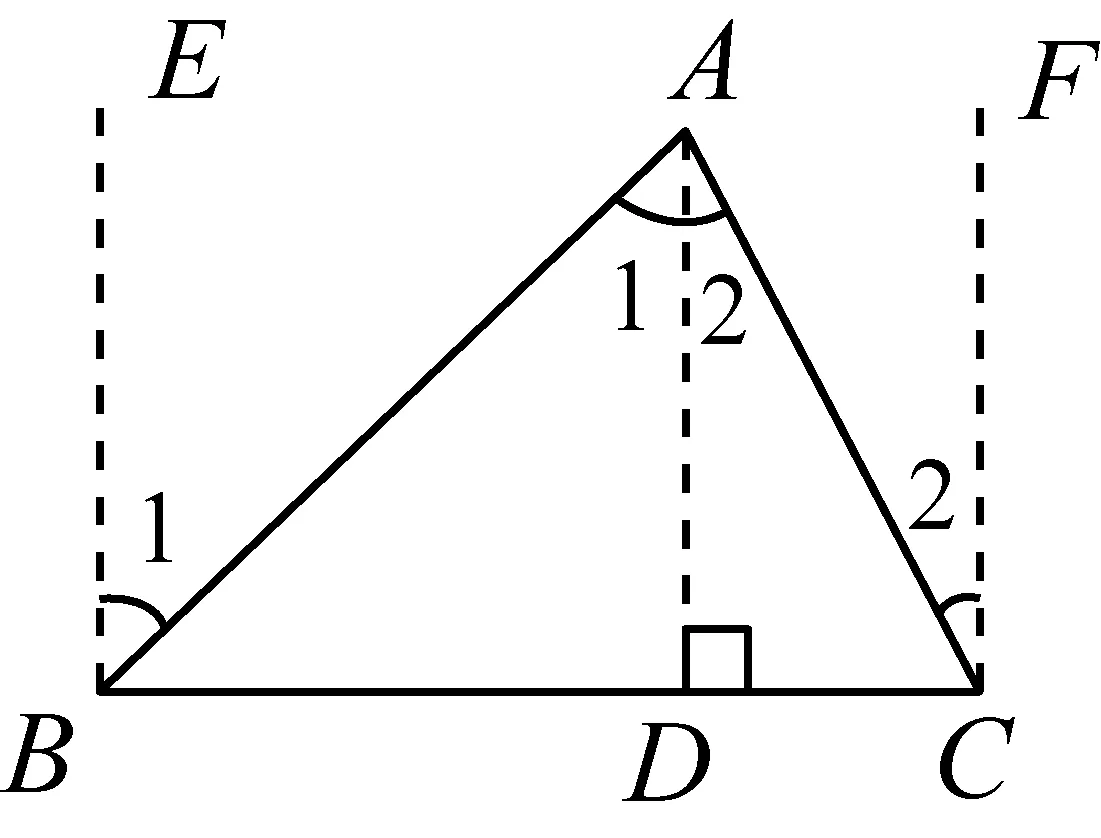
圖3 普羅克拉斯證法1

圖4 普羅克拉斯證法2

圖5 克萊羅的證明方法

此外，在18—20世紀英美一些教科書里分別過邊上任意一點、形外一點、形內一點作平行線，給這個定理增加了多種新的證明方法(如圖6)[8].

圖6 英美早期教科書證明方法

從歷史發展來看，人類對這個定理的認識從公元前6世紀延續到今天，展示了它強大的“生命力”，多種多樣的證明方法也為本節課定理證明的教學提供了多方面的啟示.

首先，為什么產生如此多的不同證明方法？面對180°產生聯想的角度不同，則影響著思維的走向.比如畢達哥拉斯、歐幾里得、英美教材中的多種證明方法都是通過平角解決問題，而克萊羅、普羅克拉斯的方法則是通過平行線下的同旁內角互補解決問題，這是教師引領學生探究證明方法多樣性的“點撥思維的風向標”，也是實現“知何由以知其所以然”的關鍵之一，還是教學生“由果索因”發展邏輯推理能力的重要抓手，這對剛剛跨進幾何證明大門的七年級學生來說尤為重要.

其次，眾多方法的共性是什么？在“異”中發現“同”——利用平行線轉化角，這是對數學方法的抽象，在提煉轉化思想的過程中促進學生的深度思考.為什么古代數學家們都要作平行線？因為三角形的三個內角是分散的，需要將“角”集中到一起形成平角或同旁內角，“轉移角”成為必須，而平行線可以通過生成相等角實現轉移，這何嘗不是實現“知何由以知其所以然”的另一個關鍵所在.

最后，為什么從公元前6世紀直到20世紀，橫跨2000多年，這一偉大的定理的驗證、證明方法一直保持著活力與生機？是什么力量支撐著人們追求多種方法驗證結論、證明結論？這顯然是人類在認識自然過程中，一種自我挑戰信念的傳承與發展，這是在課堂教學中實現德育之效的“活素材”.

3 課堂實錄與課后反饋

3.1 引入新課

PPT放映形狀大小不一樣的三角形若干.

師：在不一樣的事物中研究并發現事物的共同特征是數學的任務也是數學的魅力，你能說出這些形形色色的三角形具有什么共同特點嗎？

生1：兩邊之和大于第三邊、兩邊之差小于第三邊；三個內角的和等于180°.

師：研究幾何圖形常常從邊、角兩個方面入手，其中邊的數量關系在第7章曾經研究過，今天主要研究三個內角的和等于180°.(板書)

師：你是怎么知道這個結論的？

生1：我是證出來的.

生2：用量角器量每個角的度數，加起來，可得180°.

生3：拼圖拼出來的.

師：通過前面學習我們知道，生活中很多事情眼見不一定為實，度量會產生誤差，拼圖也是如此，所以需要嚴格的證明.同學們的思路定是不拘一格、各有特色的，證明方法可能不止有一種，下面大家就各顯神通一起探究吧.

片段解讀初步體會研究數學的任務之一是發現變化中不變的結論；幾何圖形的“抓手”是邊、角；“喚醒”證明的必要性，鼓勵不同證明方法，為下一步教學做準備.

3.2 證法探尋

師：我們首先將文字語言轉化為圖形與符號語言.

已知：如圖，△ABC有三個內角∠A、∠B和∠C.求證：∠A+∠B+∠C=180°.

圖7

師：你是怎么證明這個結論？(指向前面回答“證明”的生1)

生1：我是利用外角性質證明的.

(在教師追問中得知，生1 掌握的三角形外角性質是由三角形內角和等于180°得來的，這可能是受第7章教材相關內容影響，學生發現自己落入“旋渦”，并在師生對話中明白這是循環論證，在證明過程中是要不得的，不少學生恍然大悟.)

生4：我想到一種證明方法……(同畢達哥拉斯方法，過程略).

師：你是怎么想到這樣證明的？

生4：是平行線讓我想到的.

師：你是怎么想到作平行線的？

生4：這樣可以用“兩直線平行，內錯角相等”來證明角相等.

師：為什么要證明角相等，為什么要轉化角？

生4：因為三個角很分散，要集中到一起.

師：很好！最終是借助哪個特殊的角證得180°的？

生4：平角.

師：這說明，由結論中等號右邊——180°，可以聯想到平角；等號左邊是三個分散的角，將它們集中到一起成為必須，從而聯想到平行線可以轉化角，于是將問題解決.

(教師在黑板上寫下詳細證明過程)

師：這是“由果索因”的思維過程，它是打開證明思路的一種重要的方法，在寫推理的過程時，是從已知或輔助線作法一步步推“果”的過程，這是“由因推果”的思考方法，當“因果打通”時，問題便得到解決.

師：我們可以感受到證明過程步步有根有據、言必有據的理性力量，從此運用這個結論時，底氣就足了.我們把經過證明的真命題叫“定理”，它可以作為其它命題的證明或計算的依據.

師：有不同的證明方法嗎？

生5：由180°我想到了由平行線得同旁內角互補.

師：看來面對同樣的 “果”，聯想到的“因”可能不一樣，則會影響著證明的思維走向.

(教師在黑板上畫出圖形，學生根據圖形說明了完整的思路，同克萊羅的證明方法)

師：還有其它方法嗎？

隨后生6用歐幾里得的證明方法，根據老師畫出的圖形說明了完整的思路.

片段解讀在對證明思路的不斷追問中，將學生“潛在思維過程”顯性化，解釋添加輔助線的原因與目的，滲透“由果索因、由因推果”的證明思路，輔助學生邁好證明的第一步，努力達成幾何教學三境界：知其然，知其所以然，知何由以知其所以然，以此實現邏輯推理能力落地.在歷史的啟發下，鼓勵并給學生呈現不同證明方法的機會，體會證明方法的靈活多樣，享受探究之樂.

3.3 古今碰撞

師：早在2000多年前，人們就發現了這個結論，同學們觀看下面這個視頻，你會了解得更多.

(教師播放“史話三角形內角和”小視頻.視頻勾勒了從泰勒斯基于拼圖發現結論到帕斯卡通過折疊、提波特通過旋轉驗證結論，從畢達哥拉斯學派證明結論，到近代數學家不斷用不同方法證明結論的歷史演進.其中英美教材的證法，沒有展示“點”在形內，該證明思路作為課后作業.)

師：(視頻播放結束后，指明生5、生6的證明方法分別是克萊羅、歐幾里得的證法)看來同學們剛才在重演歷史.在英美教材中的證明方法的啟發之下，還有其它證明方法嗎？

生(齊)：“點”可以取在三角形內.

師：縱觀如此多的證明方法，發現有什么共同特征？

生(齊)：都用平行線轉化角.

師：既然泰勒斯已經通過拼圖發現、驗證了這個結論，為什么帕斯卡、提波特還要用不同的方法驗證？既然畢達哥拉斯已經對定理進行了證明，為什么后人還在追求不同的證明方法？這體現了人類在認識世界時的一種什么力量？

生(你一言我一語)：創新、探索、鉆研、自我挑戰……

師：這是數學帶給人們一種向上的信念.

片段解讀通過附加式運用數學史，首先，可以拓寬學生知識視野，在眾多的方法中，提煉共同的特征——利用平行線轉化角，感受方法之美，落實數學抽象.其次，在老師“小畢達哥拉斯、小克萊羅、小歐幾里得” 的稱呼中，讓學生享受成功的喜悅.再次，在縱向歷史發展進程中，讓學生對數學證明本身有更深刻的認識，在多種方法的熏陶之下，向上信念油然而生，發揮了數學史在培養理性精神，激發積極情感，樹立正確數學信念方面的作用[9].

3.4 學以致用

1. 如圖8，∠ACD是△ABC的外角，已知∠A=70°，∠B=40°，求∠ACD的度數？

圖8

圖9

2.已知直角三角形的一個銳角等于35°，求另一個銳角度數.

3. 已知(如圖9)，AC、BD相交于點O，求證：∠B+∠A=∠C+∠D.

4.已知，△ABC三個內角度數之比是2∶2∶5，求三個內角的度數.

片段解讀第1、2題，體現定理在運算過程中作為依據，并在學生解決問題之后，改變角的度數、再求解，并觀察結果，發現結論并表達結論，在從特殊到一般的過程中(這也是泰勒斯、普羅克拉斯發現、證明三角形內角和等于180°的歷程)，分別為兩個推論的生成作鋪墊，并將證明推論作為課后作業.第3題，體現定理在推理過程中作為依據.第4題，表明定理也可以作為列方程的相等關系.

3.5 課后反饋

課后，我們通過問卷調查進一步了解了學生的收獲和體會.問及“有助于我們證明一個命題的思想方法有哪些”時，學生給出了由果索因及由因推果、添加輔助線、轉化等等思考問題的方法，這表明學生對“何由以知其所以然”有了一定的體悟.在“看到‘證明’你會想到什么”的問題回答中，學生提到了公理、定理、嚴謹、由果索因、由因推果、言必有據、方法多樣性、不可以循環論證等等，這節課的主題是“證明”，顯然經過這節課的學習，學生對“證明”的概念意象更加豐富.

多種證明方法的探索對學生認識和情感上都有較大影響，有學生發出“許多證明方法，而且很巧妙，讓我茅塞頓開”的感嘆；有學生思考了方法論問題，“抓住問題核心(180°)，可以從多角度深入得到結果”；也有學生對數學本身有了更多的思考，“數學很美，一個命題可以有多種證明方法”、“數學具有理性精神”.這些方法的歷史背景也發揮了獨有的價值，培養了學生自信心，有同學回答“我和畢達哥拉斯的方法是一樣的，仿佛我和數學家進行了思想碰撞”，培養了學生的數學興趣和挑戰精神.同學們還提到“定理證明的歷史悠久，讓我對數學感興趣”、“三角形內角和等于180°原來在2000多年前就證出來了，后來還有這么多證明方法，說明人們具有探索挑戰的精神”、“都是轉化的思想，體現了創新、探索、自我挑戰的一種精神”等.

還有學生提出了想進一步了解的疑惑或問題，如“歐幾里得是怎么寫《幾何原本》的？”“公理是怎么來的？”“還有其它方法證明這個定理嗎？”“數學家遇到困難的時候，他們是如何克服的？”等等.

從反饋不難看出，數學史可以在學生的心中播種下理性、好奇、興趣、積極信念等充滿希望的“種子”，也為剛剛入門幾何證明的七年級學生邁好證明第一步“添磚加瓦”.

4 教學反思

4.1 以史為綱，解讀教材編寫結構

結合歷史發展，仔細分析蘇科版教材，筆者認為教材為學生本節課學習做足了“心理上”、“技術上”的準備.具體地講，一方面，在第7章第5節“多邊形的內角和與外角和”這一節中，基于實驗幾何(小學拼圖學習經驗)發現了三角形內角和為180°的結論，接著在動態過程中猜想了結論的合理性，進行了初步說理；另一方面，在第12章第1、2節，分別對“定義與命題”進行了介紹、對“證明的必要性”進行了闡釋，對“證明命題步驟”進行了說明.兩條線索交織，以三角形內角和定理的嚴謹多樣化證明為載體，進一步洞悉證明思路、認識證明特點的教學便是水到渠成.對比歷史，人類對該定理的認識，起源于泰勒斯的拼圖，發展于諸多數學家的實驗操作，成就于眾多數學家的多樣化的證明，人類這一漫長的認識過程，在教材的相關章節里逐一呈現，真可謂“草灰蛇線、伏脈千里”.

4.2 以史為鑒，深化課堂教學設計

研讀相關歷史，多樣化的證明方法在浩瀚歷史長河中熠熠生輝，進而促使筆者思考方法的靈活多樣性及其背后的共性、產生的原因等，為深化課堂教學設計提供了靈感.要給學生開放的探究機會，以問題引導學生分析思維過程，以達到不但“知其然”、“知其所以然”，而且“知何由以知其所以然”，這是學生邁好“幾何證明”第一步的良機，是促進學生思維更加靈活深刻的寶貴資源，是培養學生積極信念的活素材.

數學史除了隱性地啟發和影響教學，也顯性地走進了課堂，通過微視頻的形式附加式展示三角形內角和從發現、驗證到證明的發展過程.學生見識多種證明方法，體會不一樣的證明方法是“由薄到厚”的過程，面對紛繁多樣的證明方法，提煉發現運用平行線轉化角的共同思維特點是“由厚到薄”的過程，在雙向貫通中感受數學家不斷求索的探索創新精神，體會方法的嚴密美、靈活美.

此外，第7章已經學習了“多邊形外角和是360°”這一結論，不排除學生用三角形的外角性質“證明”三角形內角和定理的可能，犯循環論證的錯誤.課上學生的確出現了類似的想法，教師及時抓住學生想法，因勢利導，創造了滲透公理化思想的契機.

4.3 以史為泉，澆灌學生思維之花

由于受課堂教學時間的限制，在小視頻里只是提及了帕斯卡通過折疊、提波特通過旋轉驗證結論，也許是學生對拼圖已經很熟悉，也許是受數學家們鉆研精神的影響，課后好幾位學生前來與筆者討論帕斯卡、提波特的方法，有對自己琢磨出折疊驗證到結論后的喜悅，有對旋轉法是怎么操作的渴望，這無形之中引領學生在動手操作的數學實驗中啟思明理，讓筆者深感數學史如一股甘泉，澆灌著學生思維.

更值得一提的是，有學生在完成課后作業——過三角形內一點作平行線證明結論之后，與筆者討論，他認為畢達哥拉斯等的證明方法是過三角形頂點作邊的平行線，可以統一為過三角形的一邊上的點作平行線，因為只是邊上一點的特殊情況，由此提出這樣的觀點：證明這個定理就是在三角形所在的平面內，任取一點作邊的平行線即可，所以那么多方法，便可以看成是一種方法.當筆者聽到如此“高論”時，情不自禁地為這位剛入初中大門不久的七年級學生能具有如此深刻的認識感到欣慰.這何嘗不是對眾多方法進一步提煉，進一步“由厚到薄”的過程？讓學生經歷思考的過程，積累探索的經驗，是達成“知何由以知其所以然”的關鍵.在厚重的數學史的澆灌之下，學生的思維之花綻放得如此燦爛！