初中代數學習中發展學生推理能力的著力點分析與建議

江守福 章 飛 顧繼玲

(1.青島市教育科學研究院 266023；2.江蘇第二師范學院科研處 211200；3.南京師范大學教師教育學院 210079)

推理是數學的基本思維方式，為此，《義務教育數學課程標準(2011版)》要求[1，7],推理能力的發展應貫穿在整個數學學習過程中，并在教材編寫建議中指出[1，65],無論是“數與代數”“圖形與幾何”還是“統計與概率”的內容編排中，都要盡可能地為學生提供觀察、操作、歸納、類比、猜測、證明的機會，發展學生的推理能力.但，高中教師反映，初中生代數領域的推理能力難以應對高中階段代數學習的要求.這固然更多地是由于初中有關代數運算學習要求與高中銜接不夠所致，但在現有的課程框架下，也有必要重新審視初中代數教學中是否切實重視了學生的推理能力發展.而從一線實踐和教學研究看，對于初中階段代數領域發展學生推理能力的研究確實很少.為此，有必要再次梳理代數領域發展學生推理能力的具體著力點，分析教材編寫和教學中如何外顯數學推理，從而更好地指導一線教師在代數領域加強數學推理的教學.

1 代數領域推理能力發展的著力點分析

推理分為演繹推理和合情推理(包括歸納、類比、統計推斷等).演繹是從一般到特殊的推理，歸納是從特殊到一般的推理，類比則是特殊的具體到另一個具有某種類似特殊性的具體.因此，代數里面的推理也包括演繹推理、歸納推理和類比推理.例如，從若干運算結果中歸納出有關運算規律，就是歸納；根據運算法則推演出運算的規律或者公式，就是演繹；而根據有理數的運算法則得到無理數的運算法則、實數的運算法則等就是類比.

分析代數領域推理能力發展的著力點，需要分析整個代數學習的結構.代數的學習內容，大致是這樣一個二維的結構(如圖1).對于一個具體的研究對象(如有理數、實數、整式、分式、方程等)，縱向上大致依次研究三個方面的問題：概念、運算(包括運算法則、運算規律或公式等)、應用.橫向上，則從一個對象的研究拓廣到另一個對象的研究，如從有理數到實數的延拓、從數到式的延拓、從式到“式與式之間關系”(函數、方程、不等式)的延拓.整個初中階段的代數學習就是這樣，從現實背景出發，按縱、橫兩個方向生長，教科書也是基本按照這樣的邏輯生長起來的.圖中以序號①-⑦表示了不同的知識生長過程.下面分別分析這些生長過程中蘊含的數學推理.

①基于現實抽象代數概念，具體過程如下：從現實中抽象出有關概念的若干原型，接著對這些原型進行歸納，歸納其共性，最終概括出概念及其定義.例如，通過現實抽象出若干具體的一元二次方程，接著歸納這些方程的共同特征：含有一個未知數的整式方程，未知數的最高次數是二次，進而概括出一元二次方程的概念：形如ax2+bx+c=0這樣含有一個未知數且未知數的最高次數是二次的整式方程.其中對若干原型共性的歸納過程，具有歸納推理的成分.

②在代數概念的基礎上建立該概念相關的運算法則，常見的作法也是從現實背景中抽取若干算式，根據算式歸納法則.例如，有理數的運算法則，可能是從生活背景中兩個相反方向的連續運動得到若干算式，并根據現實意義得到算式的結果，基于這些結果歸納運算法則，當然，歸納完畢，還可進一步進行有關生活的解釋.總體而言這個過程中，多為歸納推理.

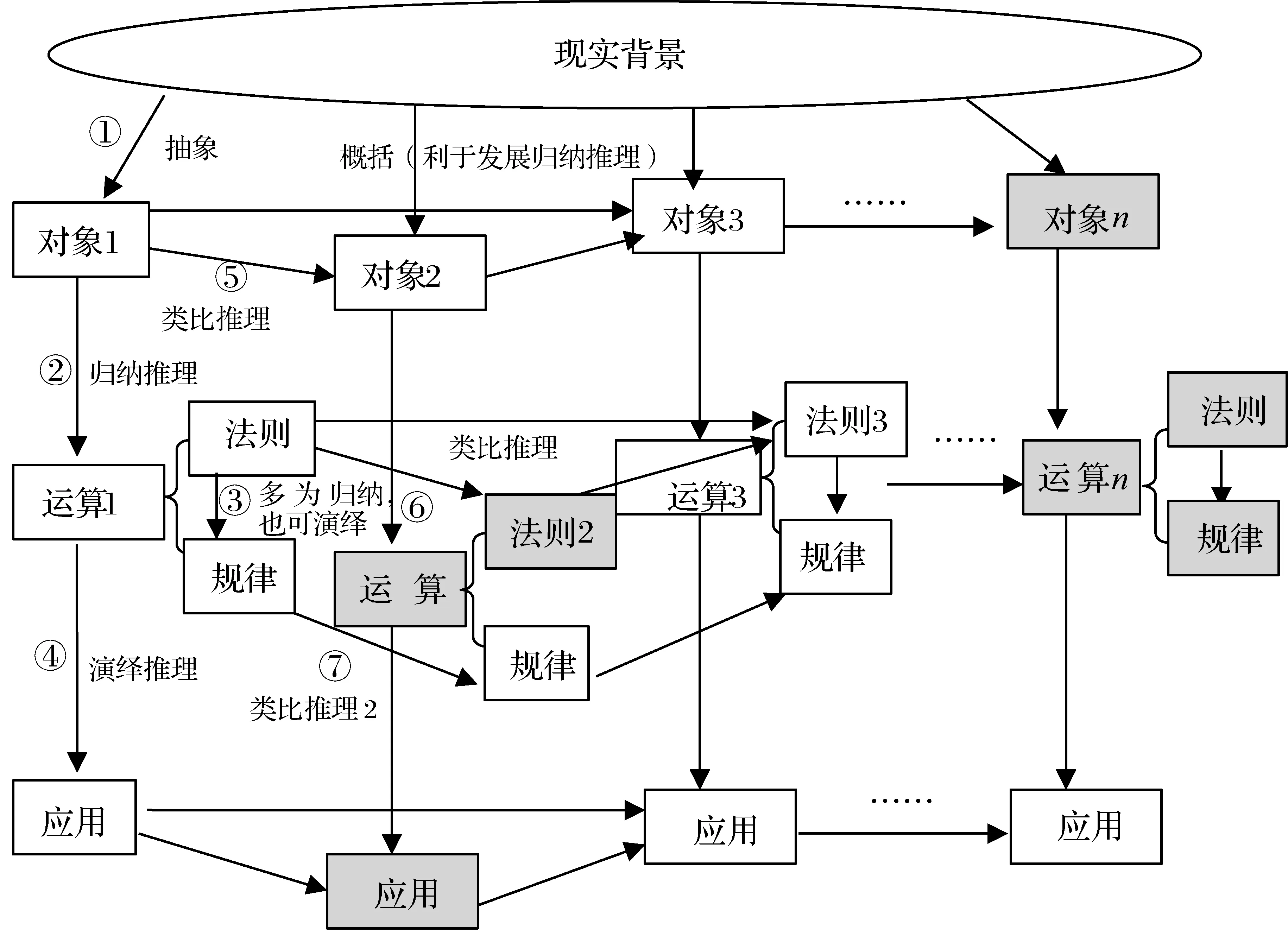
圖1 代數知識的生長示意圖

③基于運算規律探析運算規律或者運算公式.這里可能兩條思路.一是，完全基于法則進行推演，如基于多項式乘法法則推演乘法公式，這里側重的是演繹推理；二是，基于具體算式的歸納，通過對若干具體算式計算之后的觀察歸納出有關公式，這里側重的是歸納推理.

上述①-④,反映了代數對象的縱向生長，但，日常教學中常有前期類似的學習經驗，因此，代數學習中常可能產生橫向的類比拓廣，例如從有理數的概念延拓到實數的概念，從有理數加法法則延拓到實數的加法法則，從有理數的運算律(如交換律、結合律)延拓到實數的運算律，這就是⑤⑥⑦.⑤⑥⑦的學習多為類比延拓，側重的是類比推理.如由正數加法法則到有理數加法法則，原來參與運算的數是正數，現在延拓到了負數，自然正數部分的運算法則要保持一致，正數加正數仍是正數，還是按照原來的法則，結果變大；類似地，可以類比，負數加上負數，應該仍是負的，而且負得更多，結合現實情境，可以類比得出它們的絕對值相加；負數與正數，那自然可以適當抵消.再如，有理數運算到實數運算，對于初中生而言，沒有必要也沒有可能仔細介紹實數運算法則的探究推理過程，教學中一般直接點出可以類比得到：實數與有理數一樣，可以進行加、減、乘、除、乘方運算，而且有理數的運算法則與運算律對實數仍然適用.

綜上，初中代數學習中，歸納推理主要體現在①②③三個環節，類比推理主要體現在⑤⑥⑦三個環節，演繹推理主要體現在④這一環節，部分學習對象的③這一環節也可體現演繹推理.

2 代數領域推理能力發展的現狀分析

2.1 演繹推理過程簡略，師生難能體會

正如上述分析，代數領域的演繹推理主要體現在運算的應用環節，應該說，這本是代數學習中十分重要的環節，在代數學習中占有很大的篇幅.但與一線教師的交流表明，師生并未感受到其中豐富的演繹推理.這一方面是由于師生多將運算過程簡單地等同于代入公式或利用法則運算，并沒有把其視為演繹推理的過程.當然，深層次的原因是，教材設計和教學實施中，全部采用了簡化的過程，師生難能體會到其中的演繹推理.

2.2 合情推理素材豐富，但明確性不夠

正如上述分析，歸納、類比等合情推理體現在上圖中①②③⑤⑥⑦這些環節，顯然，合情推理在代數學習中同樣占據了較大的篇幅，特別是運算法則和運算規律的探究環節，但很多地方對于合情推理的過程體現尚顯不夠,很多地方多直接點明“類似地，×××同樣具有×××性質”，而缺少較為充分的探析過程.

2.3 合情推理與演繹推理的融合不夠

一個嚴格的推理過程，一般應包括從合情到演繹的全過程.但教材設計和教學實施中，這一閉環并未形成.很多法則、公式的探究僅僅停留在合情推理的層面，在歸納、類比得到有關法則、規律之后沒有進行較為嚴格的演繹推理.誠然，部分法則、規律(如實數的運算法則和運算規律)的嚴格證明確實超出了初中生的學力水平，教學中可以適度滑過，但即便如此，也可以具體案例的解釋和驗證使得學生形成更為豐富的體驗；另外，也有不少法則、規律的嚴格證明，并未超出學生的學力水平，但教材設計和教學實施中，并未進一步引導學生開展相關演繹推理活動.

2.4 未將推理能力發展作為明確的目標

教材設計和教學實施中，多將推理作為知識學習的具體工具，通過歸納、類比等得到代數的運算法則、運算規律，通過演繹等進行代數運算，但代數學習中，很少有例習題專門訓練或考查學生推理能力的發展.

3 代數領域加強推理能力發展的建議

3.1 外顯推理過程，讓推理的過程“看得見”

很多師生未能很好地“感受到”代數學習過程中的推理，部分原因是教材設計和教學實施中，代數推理的過程展開不夠.為此，需要將代數學習中的推理過程更好地展現出來，讓推理過程“看得見”.具體地，讓忽略的、壓縮掉的推理過程恢復過來，讓不完整的推理過程恢復完整.下面僅以演繹推理過程的外顯化和推理閉環的外顯為例加以說明.

演繹推理過程的外顯化學生能很好地感受幾何學習中的演繹推理，因為，幾何學習中很清楚地給出了三段論式的演繹推理過程，而代數中沒有給出三段論式的演繹推理過程.當然，如果所有代數運算中都完整地展現三段論式的演繹推理過程，過程較為拖沓，師生難免厭煩，而且算式也不連貫.面對這個兩難境地，可以適度簡化.實際上，幾何學習中，三段論式的演繹推理過程也做了一些簡化.完整的三段論式的推理模式是：大前提，小前提，小結論；這里的大前提實際上就是依據的原理、公理、定理等.但隨著學習的深入，新學習的定理(大前提)已經深入人心，要求每次寫出大前提作為依據，學生難免厭煩，而且易于形成思維阻隔現象，因此，幾何學習中，僅僅在新學習一個定理時，要求將這一定理作為證明的依據寫出，后面會逐步刪去這個大前提.考慮到刪去大前提前后的推理表達形式的一致性，數學教育工作者“創造性”地將大前提放到括號中，為后續刪減提供了便利.也就是說，幾何演繹推理形式的演變如圖2.類似地，代數運算中，也可以采用類似的做法：新學一個運算法則或運算規律，利用它們進行運算時，要求學生說明道理，即每個等號一行，在每一行算式后面標注理由，等學生熟悉之后，不再作出類似要求.這樣做，并沒有增加學生太多的負擔(僅在新法則運用的初始階段，而且對于解方程而言僅僅是在初次學習時在每行等式后面標注理由)，而將重心放到幫助學生理解和盡快熟悉新學習的有關法則、規律上，更重要的是，讓學生充分感受到代數推理的嚴謹性，養成學生言之有據的習慣.

圖2 幾何推理形式的演變

圖3 某教科書中根式乘法探析過程

3.2 設計推理任務，讓推理的目標“能達成”

推理不僅是學習的手段、工具，更是學生發展的目標.代數學習過程中，學生在運用推理的過程中，順帶發展了推理能力，但仍需要進行專門的推理訓練，通過更為豐富的推理活動發展學生的推理能力.建議，設計更有針對性的推理任務，確保推理目標的達成.這樣的任務是多樣的，可以是明確要求的歸納、類比或證明活動，也可以是對有關推理過程的判斷、辨析、完善與改進等.例如，設計一個具體的活動，要求學生在活動中經歷歸納、猜想與證明的過程，切實感受推理的全過程；再如，可以呈現一些推理的過程(如解方程、解不等式或者其他運算的過程)，要求學生判斷這樣的推理過程是否正確并加以完善、改進.茲舉幾例，與同行交流.

例1(1)嘗試用分數表示各分數的和(略).

(2)根據(1)的結果，有人說“兩個有理數的和還是一個有理數”，你認為這個說法正確嗎，請給出你的證明.

(3)一個有理數與一個無理數的和，是有理數還是無理數？

(4)*兩個無理數的和一定是無理數嗎？(*為選做題，根據學生學力靈活處理)

(5)*關于兩個數(有理數或者無理數)的積，你有哪些猜想，你能證明你的猜想嗎？

例2下列解方程的過程是否正確(略)？正確的說明每一步的依據，錯誤的加以改正.

例3如圖4，8個相同的直角三角形和一個小正方形組成了一個大正方形.

圖4 某教科書中根式乘法探析過程

(1)不進行計算，僅觀察圖形，說說(a+b)2-(a-b)2的結果和理由.

(2)用代數方法證明(1)中發現的結論.

總之，推理能力的發展，同樣是初中代數學習的重要目標.為此，在教材編寫和教學設計中，應認真梳理代數學習中發展學生推理能力的著力點，審視代數教學中發展學生推理能力的薄弱環節，通過外顯推理過程和明確的推理任務等多種方式，切實發展學生的推理能力.