改進物質點法及其在爆炸與沖擊動力學中的應用

陳衛東， 劉瀾， 路勝卓， 吳世博， 馬敬鑫， 吳培文

(哈爾濱工程大學 航天與建筑工程學院，黑龍江 哈爾濱 150001)

物質點法(material point method，MPM)是一種由粒子算法與網格算法相結合的數值計算方法。該算法最早是由Sulsky等[1]率先提出的，此后國內外許多學者都對該算法進行了深入研究，并且在時間積分[2]、形函數改進[3-5]、接觸算法[6]以及多種算法耦合[7-9]等多個方面對該算法進行了改進，從而使該算法不斷趨于成熟。因此在近年來，該算法已經在許多工程計算領域中得到了廣泛應用。

但是在爆炸與沖擊類工程計算領域中，由于計算對象往往會出現體積劇烈膨脹或結構大尺度拉伸變形等狀況，例如炸藥爆轟產物膨脹擴散以及破片飛濺等。所以在應用物質點法及其現有的改進算法求解此類問題時，當模型運行至一定階段后，往往會出現背景網格區域容量不足以及物質點陷入拉伸不穩定狀態等不利情況，這些情況會對計算結果產生嚴重影響，從而制約物質點法在爆炸與沖擊類工程計算領域中的應用。因此現有必要對物質點法作進一步改進，以使該算法能夠更加適用于求解爆炸與沖擊類工程實際問題。

1 物質點法的顯式時間積分原理

在物質點法中，計算對象被離散成一系列占據一定體積的物質點，并且被設置于背景網格之中，物質點儲存著其所在區域的材料的全部物理信息，而背景網格節點則只用于求解動量方程和空間導數。因此基于應力后更新(update stress last，USL)求解格式的物質點法顯式時間積分原理[10-11]的具體實現過程可表述如下。

1)將物質點所攜帶的質量、動量和速度映射到網格節點上，從而得到網格節點的質量、動量和速度。該步驟的具體表達式分別為：

(1)

(2)

(3)

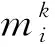
2)計算網格節點力。網格節點合力的表達式為：

(4)

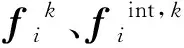
3)計算下一時間步的節點動量。該步驟的表達式為：

(5)

式中Δtk表示時間步長。

4)將下一時間步的節點動量映射回物質點，并更新物質點的速度和位置坐標。該步驟的表達式分別為：

(6)

(7)

5)計算物質點的旋率增量和應變增量。旋率增量和應變增量的表達式分別為：

(8)

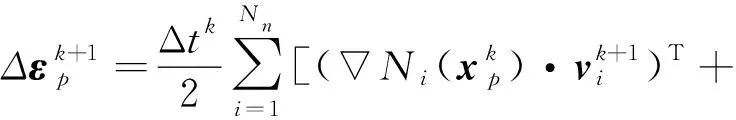
(9)

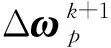
6)更新物質點的密度和幾何尺寸。該步驟的表達式分別為：

(10)

(11)

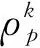
7)更新物質點的應力。該步驟的表達式為：

(12)

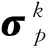
8)重復上述步驟1)～7)，直至達到終止計算時間。

2 物質點法的改進

2.1 構建物質點自由流出邊界條件

2.1.1 物質點自由流出邊界條件的作用與構建方式

根據物質點法的顯式時間積分原理可知，背景網格在每次時間積分計算結束后都會自動復原，并繼續參與下次時間積分計算。因此物質點法的背景網格區域始終處于非嚴格封閉狀態，當物質點擴散至背景網格邊界時，物質點及其所攜帶的物理信息都會受到邊界節點的約束，而無法從背景網格邊界自由流出，導致數值計算結果產生巨大誤差。所以一般應設置容積較大的背景網格區域，以盡量減小邊界節點約束對數值計算的影響。但是背景網格區域設置過大，又勢必會加大數值計算的工作量，導致計算成本大幅度提高，這是物質點法所面臨的一種局限。為了破除物質點法的這一局限，本文將基于物質點法顯式時間積分原理來構建物質點自由流出邊界條件，以使物質點及其物理信息能夠根據實際情況從背景網格邊界自由流出，從而在保證數值計算精確度的同時提高計算效率。下面對物質點自由流出邊界條件的構建方式進行具體介紹。

在每次時間積分計算開始前，都要對模型中的全部物質點進行位置坐標的重新確定，然后按照

(13)

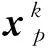
2.1.2 算例分析

為了檢驗物質點自由流出邊界條件的有效性，本文將該邊界條件應用到近物面水下爆炸算例中，并通過算例的對比分析結果來對該邊界條件的實際效果以及鋼板前后的正向沖擊波(入射波)、反射波和透射波的形態進行量化描述。在近物面水下爆炸算例中，采用基于Fortran語言自編的物質點法程序來構建3個近物面水下爆炸二維模型，這3個模型在該算例中分別簡稱為模型A、模型B和模型C，這3個模型的初始形態如圖1所示，其中，模型A和模型B的矩形背景網格區域的面積均為100.0 cm×100.0 cm，模型A施加物質點自由流出邊界條件，模型B不施加該邊界條件；而模型C的矩形背景網格區域的面積為200.0 cm×200.0 cm，且不施加物質點自由流出邊界條件。除此之外，這3個模型的其他方面都是相同的，即：直角坐標系的坐標原點均設置在背景網格區域的形心位置，網格單元尺寸均為0.5 cm×0.5 cm，背景網格區域中均填加了面積為100.0 cm×100.0 cm的矩形物質點區域，物質點區域的中心部位構建了尺寸為8.0 cm×8.0 cm的矩形TNT炸藥，炸藥右側構建了厚度為2.0 cm的鋼板，鋼板的前壁面(迎爆面)與炸藥形心的距離為250 cm，物質點區域的其他部位由水填充，離散物質點的尺寸為0.25 cm×0.25 cm，在物質點區域中從左至右依次設置了4個觀測點，這4個觀測點的坐標見表1。

通過圖1可知，模型C在其物質點區域的四周均預留出寬度為50 cm的背景網格擴充區域，從而可給物質點膨脹擴散提供充足的空間，這是應用物質點法構建數值模型的常規方式，所以模型C的計算結果可以認定是正確的，因此本算例采用模型C的計算結果來作為模型A和模型B的計算結果的正確性檢驗標準；而模型A和模型B的背景網格區域的尺寸與物質點區域的尺寸相同，并沒有給物質點膨脹擴散提供額外的網格空間，因此可通過將這2個模型的計算結果與模型C的計算結果進行相互比較，以檢驗施加于模型A的物質點自由流出邊界條件的有效性。在分別對這3個模型進行數值計算后，得到了這3個模型中4個觀測點的壓力時程數據以及這3個模型在各時刻的壓力云圖。

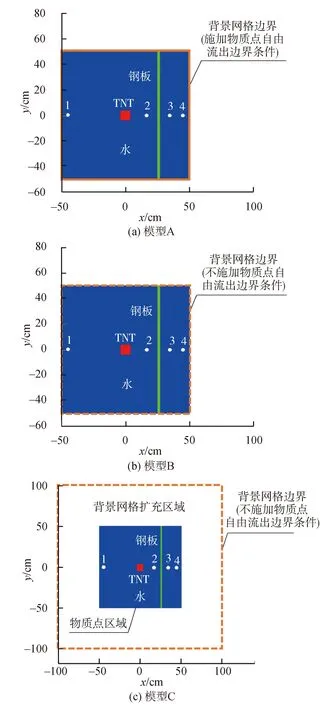
圖1 3個模型的初始形態Fig.1 Initial form of 3 models

現分別提取距離背景網格左側邊界5 cm的觀測點1和距離背景網格右側邊界5 cm的觀測點4的壓力時程數據，繪制出圖2所示的這2個觀測點的壓力時程曲線。

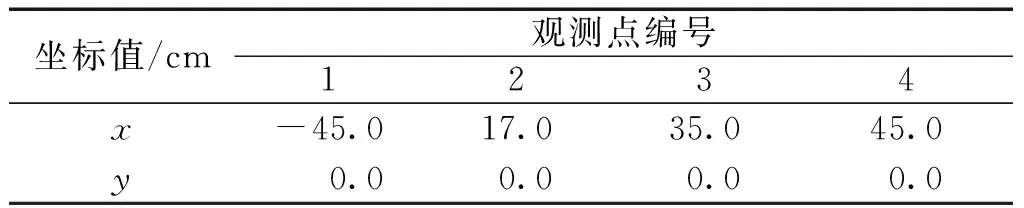
表1 近物面水下爆炸模型的觀測點坐標

通過觀察圖2可知，由于模型C給物質點膨脹擴散提供了網格空間，所以模型C中水下爆炸形成的正向沖擊波以及鋼板前后形成的反射波和透射波都能夠跟隨物質點的膨脹擴散而被自由釋放，因此在450 μs的計算時間內，模型C中這2個觀測點的壓力時程曲線都只具有1個波峰，其中觀測點1的波峰是由正向沖擊波形成的，觀測點4的波峰是由板后透射波形成的；而模型B既沒有給物質點膨脹擴散提供網格空間，也沒有施加物質點自由流出邊界條件，這導致模型B中水下爆炸形成的正向沖擊波以及鋼板后方的透射波在傳播至背景網格邊界后不能被自由釋放，并且在網格邊界產生了反射波，因此模型B在這2個觀測點位置的壓力時程曲線都具有2個波峰，其中第2個波峰都是由網格邊界產生的反射波所造成的，這與模型C的壓力時程曲線存在顯著差異；而模型A雖然沒有給物質點膨脹擴散提供網格空間，但是由于在背景網格邊界施加了物質點自由流出邊界條件，所以模型A中水下爆炸形成的正向沖擊波以及鋼板后方的透射波都能夠從網格邊界自由釋放，不會在網格邊界產生反射波，因此模型A能夠得到與模型C十分相近的數值計算結果，從而使模型A和模型C在這2個觀測點位置的壓力時程曲線高度重合。

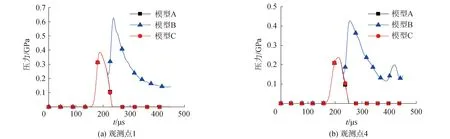
圖2 3個模型中觀測點1和觀測點4的壓力時程曲線Fig.2 Pressure history of observation point 1 and 4 in 3 models

再通過觀察圖3所示的3個模型第300 μs的壓力云圖可知，由于模型C給物質點膨脹擴散提供了網格空間，因此在模型C的壓力云圖中，能夠清楚的觀察到物質點區域的膨脹變形過程和壓力釋放過程；而模型B既沒有給物質點膨脹擴散提供網格空間，也沒有施加物質點自由流出邊界條件，因此模型B水下爆炸形成的正向沖擊波以及鋼板后方的透射波在傳播至背景網格邊界后會出現明顯的反射現象，反射波壓力峰值會達到0.3 GPa以上；而模型A雖然也沒有給物質點膨脹擴散提供網格空間，但是由于在背景網格邊界施加了物質點自由流出邊界條件，致使模型A中的部分物質點及其物理信息能夠從網格邊界自由流出，所以模型A水下爆炸形成的正向沖擊波以及鋼板后方的透射波在傳播至網格邊界后依然能被成功釋放，因此模型A的物質點區域內的壓力分布與變化情況能夠與模型C基本保持一致。

通過以上對比分析結果可知，由于模型B未施加物質點自由流出邊界條件，因此模型B的背景網格邊界是一種非嚴格封閉邊界，物質點及其所攜帶的物理信息不能從網格邊界自由流出。而模型A在背景網格邊界施加了物質點自由流出邊界條件，因此物質點及其物理信息能夠從網格邊界自由流出，從而使模型A能夠得到與模型C非常相近的數值計算結果，并且由于模型A的網格節點數量較少，物質點又能夠在計算過程中從網格邊界大量流出，因此模型A的計算效率較模型C有明顯提高，計算結果顯示，模型A的計算耗時約為32 869 s，模型C的計算耗時約為50 316 s，模型A的計算耗時僅為模型C的0.653倍。由此可知，施加物質點自由流出邊界條件的物質點模型能夠在保證計算精確度的同時大幅度提高計算效率，因此物質點自由流出邊界條件是十分有效的。

此外，為了進一步觀察近物面水下爆炸模型中正向沖擊波以及鋼板前后的反射波和透射波的基本形態，現分別提取模型A中距離鋼板前壁面8 cm的觀測點2和距離鋼板后壁面8 cm的觀測點3的壓力時程數據，繪制出圖4所示的這2個觀測點的壓力時程曲線。

圖3 3個模型第300 μs的壓力云圖Fig.3 Pressure contours regarding 3 models at the 300th μs

通過觀察圖4可知，觀測點2的壓力時程曲線具有2個峰值超過0.7 GPa的波峰，這2個波峰分別是由水下爆炸的正向沖擊波和鋼板前壁面反射波所造成的；而觀測點3的壓力時程曲線則只具有1個峰值超過0.25 GPa的波峰，該波峰是由鋼板后壁面透射波所造成的。通過觀察圖4還可知，觀測點2位置的正向沖擊波和板前反射波的峰值較高，但正壓作用時間較短；而觀測點3位置的板后透射波的峰值較低，但正壓作用時間較長，這與近物面水下爆炸的真實情況相符合。

下面分別選取圖5所示的模型A第130 μs和第170 μs的壓力云圖來對該模型中正向沖擊波以及鋼板前后的反射波和透射波的基本形態做更為直觀的觀察。

通過觀察圖5可知，在模型A中，水下爆炸所形成的正向沖擊波作用到鋼板后，會在鋼板的前壁面和后壁面分別產生反射波和透射波，且正向沖擊波和反射波的壓力峰值要高于透射波的壓力峰值，同時鋼板會發生明顯變形，這也符合近物面水下爆炸的真實情況。

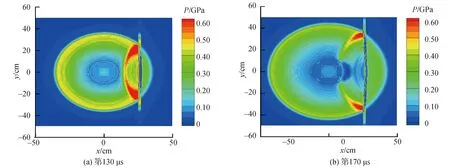
圖5 模型A第130 μs和第170 μs的壓力云圖Fig.5 Pressure contours regarding model A at the 130th μs and the 170th μs

2.2 改進物質點自適應分裂方案

2.2.1 物質點自適應分裂改進方案的作用與原理

在標準物質點法中，物質點數量在數值計算過程中是保持不變的，這會導致在計算對象沿某一方向膨脹或拉伸變形的過程中，該方向的物質點也會隨之變得稀疏，這種情況會對計算結果產生一定程度的影響，甚至會使數值計算產生嚴重的拉伸不穩定現象，這是物質點法所面臨的另一種局限[10,12]。為了解決這一問題，Ma等[12]設計并提出了物質點自適應分裂方案(adaptive particle splitting scheme)，但是該方案只能使物質點在每次時間積分計算中沿某一個坐標軸方向進行自適應分裂，而不能使物質點在每次時間積分計算中沿多個坐標軸方向同時進行自適應分裂，所以基于該方案的物質點法在多維度物質點模型數值計算中仍然具有局限性。為了徹底破除物質點法的這一局限，本文對物質點自適應分裂方案進行了改進，使物質點在每次顯式時間積分計算中能夠沿多個坐標軸方向同時進行自適應分裂，以滿足多維度物質點模型的數值計算要求，并由此形成物質點自適應分裂的改進方案。下面以二維問題為例，來對物質點自適應分裂改進方案的基本原理進行詳細介紹。

在由直角坐標系所表征的二維問題中，計算對象具有沿x軸方向和y軸方向進行膨脹或拉伸變形的可能性，因此在物質點自適應分裂改進方案中，應將物質點自適應分裂分為以下3種情況來分別進行討論。

1)只沿x軸方向進行分裂。

當物質點沿x軸方向發生膨脹或拉伸變形時，如果物質點在x軸方向上的特征尺寸達到分裂判定條件：

(14)

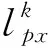
(15)

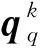
2)只沿y軸方向進行分裂。

當物質點沿y軸方向發生膨脹或拉伸變形時，如果物質點在y軸方向上的特征尺寸達到分裂判定條件：

(16)

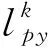
3)同時沿x軸方向和y軸方向進行分裂。

當物質點沿x軸方向和y軸方向發生膨脹或拉伸變形時，如果物質點在這2個方向上的特征尺寸同時達到式(14)和式(16)所示的分裂判定條件，則使物質點沿這2個方向同時進行均等分裂，分裂以后將產生4個新物質點，這4個新物質點的各項廣延量的數值為原物質點的0.25倍，而各項強度量的數值則保持不變，因此新物質點的各項物理量的取值方式為：

(17)

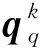
以上即為二維條件下的物質點自適應分裂改進方案的基本原理。而三維條件下的物質點自適應分裂改進方案的基本原理也與之類似，只是需要考慮物質點沿z軸方向進行自適應分裂的情況，因此存在7種分裂方式，此處不再逐一贅述。

2.2.2 算例分析

為了檢驗物質點自適應分裂改進方案的有效性，本文將該改進方案應用到聚能射流算例中，并通過算例的對比分析結果來對該改進方案的實際效果進行量化描述。在聚能射流算例中，同樣采用自編的物質點法程序構建了圖6所示的聚能射流模型(本算例中簡稱物質點聚能射流模型)，該模型的背景網格區域的面積為25.0 cm×10.0 cm，背景網格區域中構建了藥型罩錐角為60°的射流彈，射流彈的藥型罩的材料為銅，殼體材料為鋼，內裝藥為PBX9501炸藥，背景網格區域的其他部位用空氣填充，射流彈各結構的物質點的尺寸為0.05 cm×0.05 cm，空氣物質點的尺寸為0.1 cm×0.1 cm，網格單元的尺寸為0.1 cm×0.1 cm，整個模型共離散出29 440個物質點和25 000個網格單元，背景網格邊界施加了物質點自由流出邊界條件，在背景網格區域內沿著射流路徑依次設置了6個觀測點，這6個觀測點的坐標見表2。

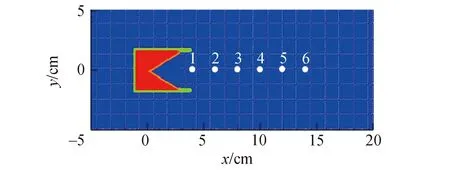
圖6 聚能射流模型Fig.6 Shaped charge jet mode

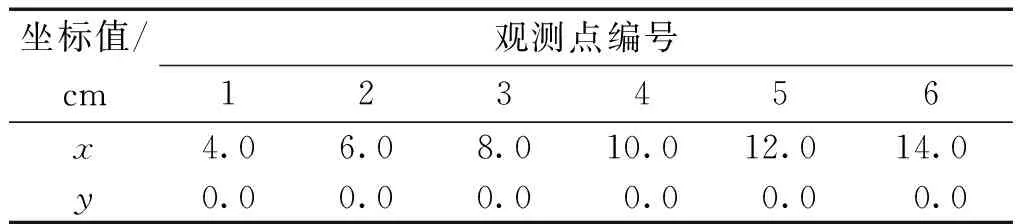
表2 聚能射流模型的觀測點坐標

此外，由于Autodyn軟件是目前公認的數值模擬爆炸與沖擊動力學問題效果最好的商業軟件之一，因此本算例運用Autodyn軟件的Euler-2D Multi-material求解器來構建與物質點聚能射流模型相對應的Autodyn二維軸對稱聚能射流模型(本算例中簡稱Autodyn聚能射流模型)，并且采用Autodyn聚能射流模型的計算結果來作為物質點聚能射流模型的計算結果的正確性檢驗標準。Autodyn聚能射流模型的Euler網格單元尺寸為0.025 cm×0.025 cm，網格邊界添加Autodyn自帶的流出邊界條件(Flow_Out邊界條件)。

然后分別對物質點聚能射流模型和Autodyn聚能射流模型進行數值計算，其中，物質點聚能射流模型的數值計算分別在啟動物質點自適應分裂子程序和不啟動該子程序這2種條件下進行，以檢驗物質點自適應分裂改進方案的有效性。數值計算完成后，得到圖7所示的第35 μs模型外觀形態對比結果以及表3所示的聚能射流頭部到達6個觀測點位置時頭部速度的對比結果，且為了便于觀察聚能射流的外觀形態，空氣介質在圖7的3張圖片中均不予顯示。

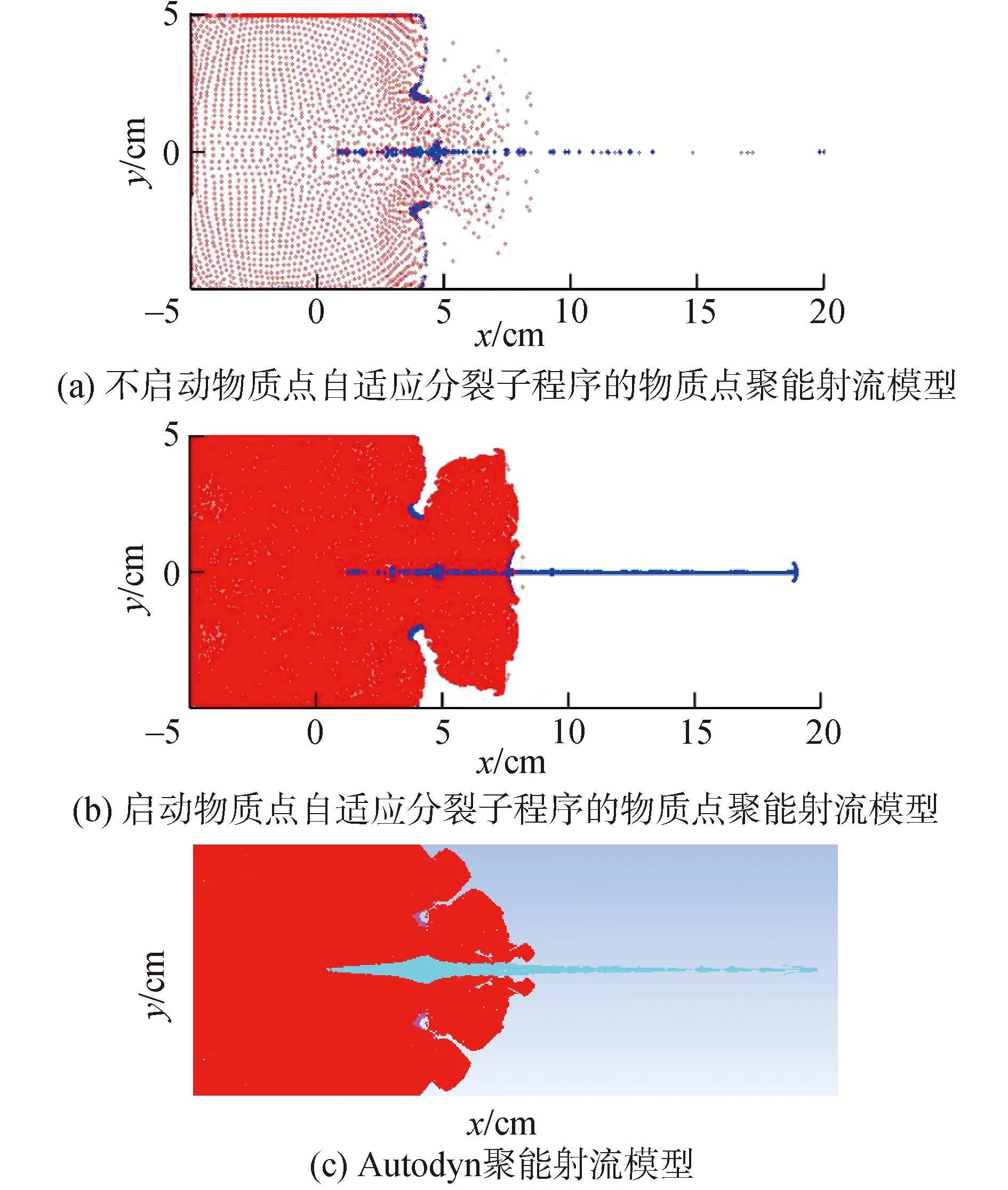
圖7 3個模型第35 μs的外觀形態對比結果Fig.7 Comparative results of the visual forms regarding 3 models at the 35th μs

首先通過觀察圖7可知，在未啟動物質點自適應分裂子程序的物質點聚能射流模型數值計算中，隨著內裝藥爆轟產物的持續擴散和銅質藥型罩的持續擠壓拉伸變形，內裝藥爆轟產物物質點和藥型罩物質點在背景網格區域內的空間分布密度逐漸降低，數值計算過程產生了嚴重的拉伸不穩定現象，以至于當物質點聚能射流模型運行至35 μs時，內裝藥爆轟產物區顯露出大面積空白區域，并且藥型罩物質點之間也發生了明顯的非物理性分離，因此所形成的聚能射流并不連續，這與Autodyn聚能射流模型的聚能射流外觀形態存在本質性差別；而在啟動物質點自適應分裂子程序的物質點聚能射流模型數值計算中，隨著內裝藥爆轟產物的持續擴散和藥型罩的持續擠壓拉伸變形，內裝藥爆轟產物物質點和藥型罩物質點在x軸方向和y軸方向上不斷進行自適應分裂，從而可保證物質點在背景網格區域內的空間分布密度不會明顯降低，有效避免了拉伸不穩定現象的產生，因此當物質點聚能射流模型運行至35 μs時，共產生出84 600個物質點(其中包括29 440個初始物質點)，此時的物質點總數約是初始物質點總數的2.87倍，內裝藥爆轟產物區沒有出現大面積空白區域，并且藥型罩物質點之間也沒有發生非物理性分離，因此所形成的聚能射流的連續性非常好，這與Autodyn聚能射流模型的聚能射流外觀形態具有較高的吻合度。

再通過表3可知，物質點聚能射流模型在未啟動物質點自適應分裂子程序的條件下，其與Autodyn聚能射流模型只是在觀測點1位置的射流頭部速度相對差值的絕對值低于4%，而在其余5個觀測點位置的射流頭部速度相對差值的絕對值均高于4%；而物質點聚能射流模型在啟動物質點自適應分裂子程序的條件下，其與Autodyn聚能射流模型在6個觀測點位置的射流頭部速度相對差值的絕對值均低于2.5%。由此可知，啟動物質點自適應分裂子程序條件下的物質點聚能射流模型與Autodyn聚能射流模型的射流頭部速度相差較小，即該條件下的物質點聚能射流模型的計算精確度更高。

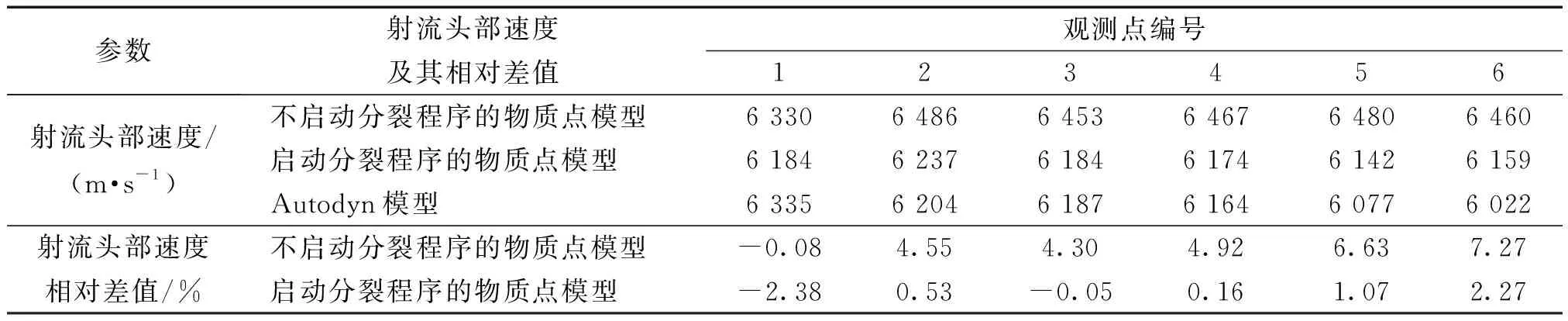
表3 3個模型在6個觀測點位置的射流頭部速度對比結果Table 3 Comparative results of shaped charge jet tip velocity by the location of 6 observation points regarding 3 models

通過本算例的上述對比分析結果可知，物質點自適應分裂改進方案能夠使物質點在每次顯式時間積分計算中沿多個坐標軸方向同時進行自適應分裂，從而可避免物質點模型的數值計算產生拉伸不穩定現象，進而使數值計算的精確度得以顯著提高。由此可知，物質點自適應分裂改進方案對物質點法的改進效果是十分顯著的。

3 結論

1) 物質點自由流出邊界條件能夠使物質點及其所攜帶的物理信息在每次顯式時間積分計算中根據實際情況從背景網格邊界自由流出，所以構建背景網格時并不需要給物質點膨脹擴散提供額外的網格空間，因此可使物質點模型在保證計算精確度的同時大幅度提高計算效率；

2) 物質點自適應分裂改進方案能夠使物質點在每次顯式時間積分計算中根據分裂判定條件沿多個坐標軸方向同時進行自適應分裂，從而有效避免了數值計算過程中拉伸不穩定現象的發生，使多維度物質點模型的計算精確度得以顯著提高；

3) 經過這2項改進的物質點法能夠更加適用于求解爆炸與沖擊類工程實際問題。