改進的稀疏度自適應多路徑匹配追蹤算法
吳夢行, 伍飛云, 楊坤德, 田天
(1.杭州應用聲學研究所 聲納技術重點實驗室,浙江 杭州 310023; 2.西北工業大學 航海學院,陜西 西安 710072)
壓縮感知(compressed sensing, CS)在過去的十幾年中,由于其在圖像和音頻處理[1]、視覺跟蹤[2-4]、以及計算機視覺和水聲信道估計[5-8]等多個領域的巨大潛在應用價值,受到了越來越多的關注。
結合測量矩陣和壓縮的信號對原始信號進行恢復是壓縮感知最重要的部分之一,其可以對采樣不足的信號進行充分的重構,突破了傳統的香農奈奎斯特采樣定理,實現了可接受的準確性和復雜度。常用的重構算法主要包括凸優化算法和貪婪迭代算法[9]。其中,貪婪算法以其兼顧重構質量和運行效率的優勢,受到越來越多的關注。匹配追蹤算法(matching pursuit)是最典型的貪婪算法之一,其特點是根據傳感矩陣與殘差值相關性的強弱,挑選最為匹配的原子擴充支撐集,其重構速度快且有較好的重構質量。其改進算法還包括OMP (orthogonal MP)[10]、ROMP (regularized OMP)[11]、 StOMP (stagewise OMP)[12]等算法。然而,挑選的原子被選入支撐集后,將在整個迭代過程中保留,無法判斷和更新錯選的原子,影響了支撐集的準確性,且相關性判據有待改進。為此,出現的CoSaMP算法 (compressive sampling MP)[13]和SP算法(subspace pursuit)[14]算法通過回溯步驟剔除相關性較低的原子,獲得更精確的支持集,但是重構效果受到支撐集原子選擇方式缺乏靈活性的約束。為了滿足在未知稀疏度K的情況下獲得更好的跟蹤和重建性能,SAMP (sparsity adaptive MP)等算法對匹配跟蹤算法進行了大量的改進[15-18]。這類稀疏度自適應算法的核心是利用一個固定步長多次迭代不斷逼近,達到事先不需要知道稀疏度就能準確估計真實的稀疏度K的目的。
在滿足稀疏性條件的前提下,MMP算法[19]從多個候選支撐集中選擇最優方案,顯然多路徑搜索比單路徑搜索有更好的性能。但由于MMP計算量大,在沒有稀疏信息的情況下很難求解大規模問題。因此對MMP算法進行優化具有重要的意義。本文在MMP算法基礎上提出了一種改進的快速稀疏度自適應多路徑匹配追蹤算法(improved multipath matching pursuit algorithm with sparsity adaptive, IMMP)。與傳統算法相比,IMMP算法具有明顯的重構精度和時間優勢。
1 壓縮感知與多路徑匹配追蹤算法
1.1 壓縮感知理論
由CS理論可知,將一個K-稀疏或在某一稀疏域能稀疏表示的N維離散數字信號通過某一個測量矩陣進行有效壓縮,我們就能夠在線性變換下通過得到少量的觀測值精確重構原始信號[10]。信號x中除了只有K個非零值外其余N-K個值均為零,且K遠小于N。采樣和壓縮過程可以描述為:
y=Φx
(1)
式中:Φ是大小為M×N的測量矩陣,觀測值y的長度為M且滿足M?N。壓縮感知理論的目標是基于觀測值y和測量矩陣Φ將重構問題轉換為求具有稀疏約束的l0范數的最優解問題。其求l0范數最優解模型為:
(2)
式中 ‖x‖0為x的l0范數。如果在某一變換域中使信號x滿足稀疏條件,稱此變換域為x的稀疏域,在此稀疏域中,信號可以稀疏表示為:
x=Ψθ
(3)
式中:Ψ=[ψ1ψ2…ψN]為稀疏基矩陣;θ為在稀疏基矩陣Ψ下的K稀疏信號矩陣。理論表明,求解最小l0范數是一個NP-hard問題[20],而且求解最小l0范數可以轉化為求解最小l1范數[11],即最小l1范數優化問題:
(4)
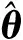
1.2 MMP算法
MMP算法通過將搜索最優路徑建模成基于樹的路徑搜索問題,每次迭代依據測量矩陣與殘差的相關性來更新一個支撐集原子,通過貪婪迭代搜索多個路徑,每個路徑經K次迭代后得到一個含K個原子的支撐集,最終達到選擇最優路徑即最優支撐集的目的。在多路徑搜索中,當前第k層分支節點原子通過計算第k-1層分支節點的殘差rk-1與測量矩陣Φ的內積確定:
Γ=arg max|〈Φ,rk-1〉|
(5)
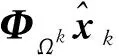
(6)
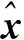
(7)
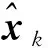
(8)
偽逆矩陣為:
(9)
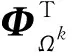
在MMP算法中,分支原子選擇的優先級由式(10)決定,其中Cl=[c1c2…cK],優先級函數layer_Order是其算法實現過程:
(10)
式中:ck與當前k層分支原子的選擇相關;d表示當前原子節點的子路徑數。Cl給予MMP搜索的第l條路徑每個節點原子被選擇的優先級,直至殘差值滿足一定停止迭代閾值ε1或達到最大搜索路徑數LMAX時停止搜索。
layer_Order函數的實現步驟如下:
1) 輸入當前路徑次序當前路徑次序l,子路徑d,稀疏度K,初始值j=1,p=l-1并計算余數cj=mod(p,d)。
2) 計算p除以d的商并賦值給p,如果j≤K,更新迭代j值:j=j+1,并轉步驟1);否則停止迭代,輸出當前路徑節點搜索順序Cl=[c1c2…cK]。
MMP-DF算法步驟如下:
1) 輸入觀測向量y,測量矩陣Φ,稀疏度K,子路徑d,最大路徑迭代次數LMAX和停止迭代閾值ε,初始值l=0,rmin=y,Ω0=?,r0=y。
2) 如果l
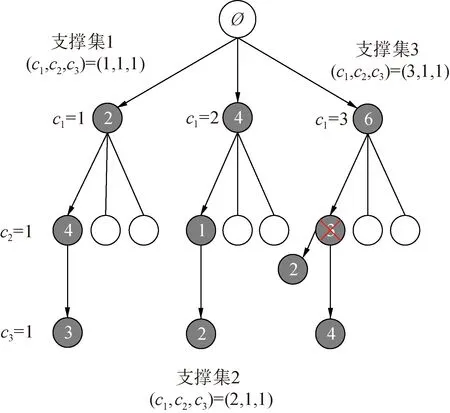
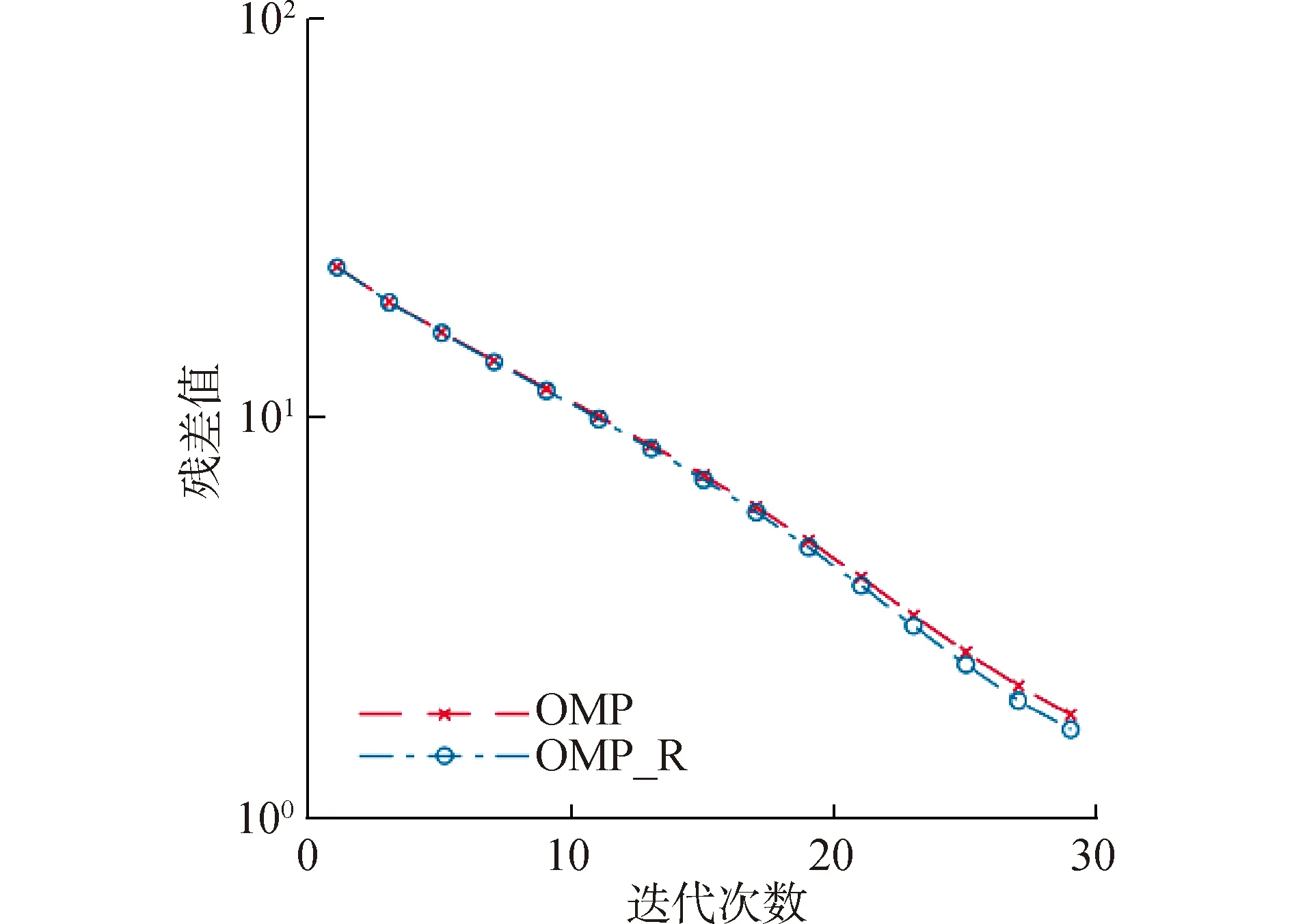
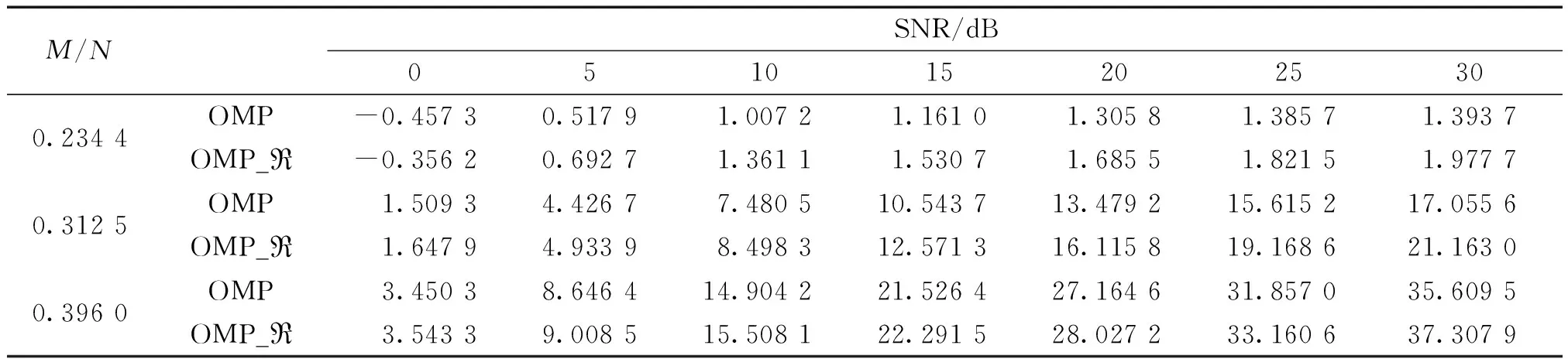
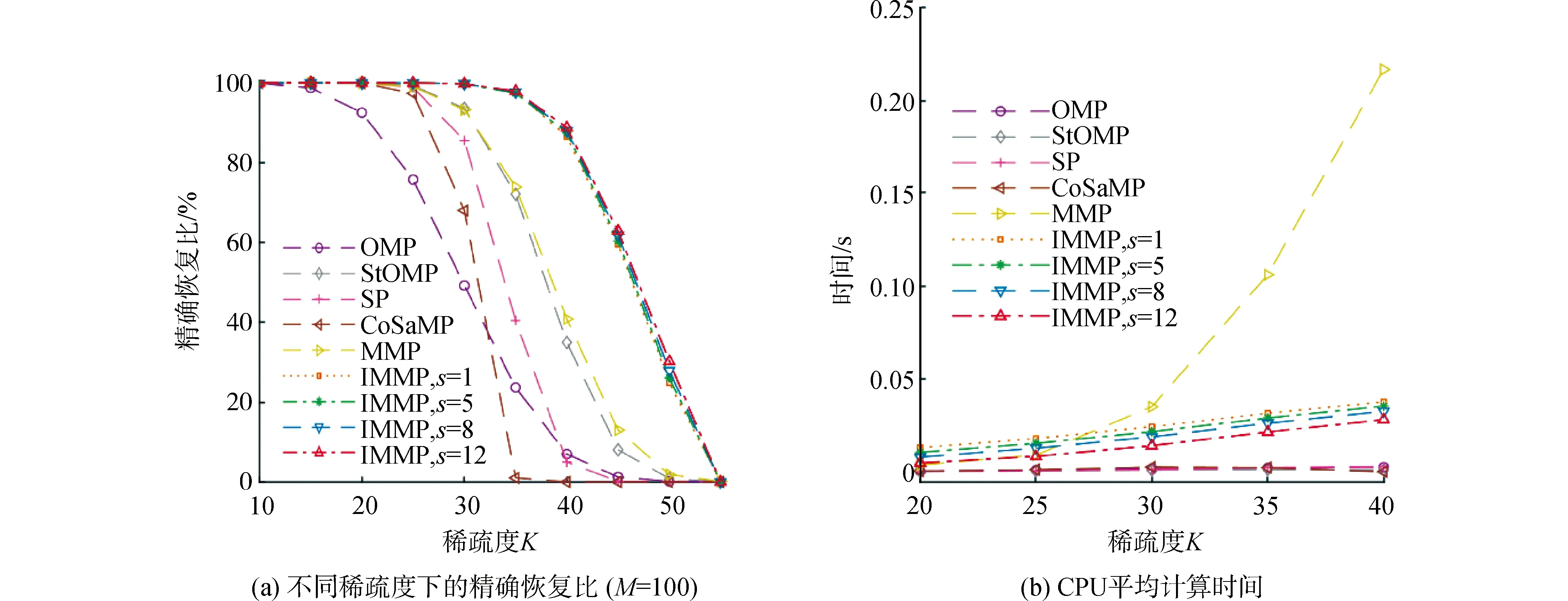
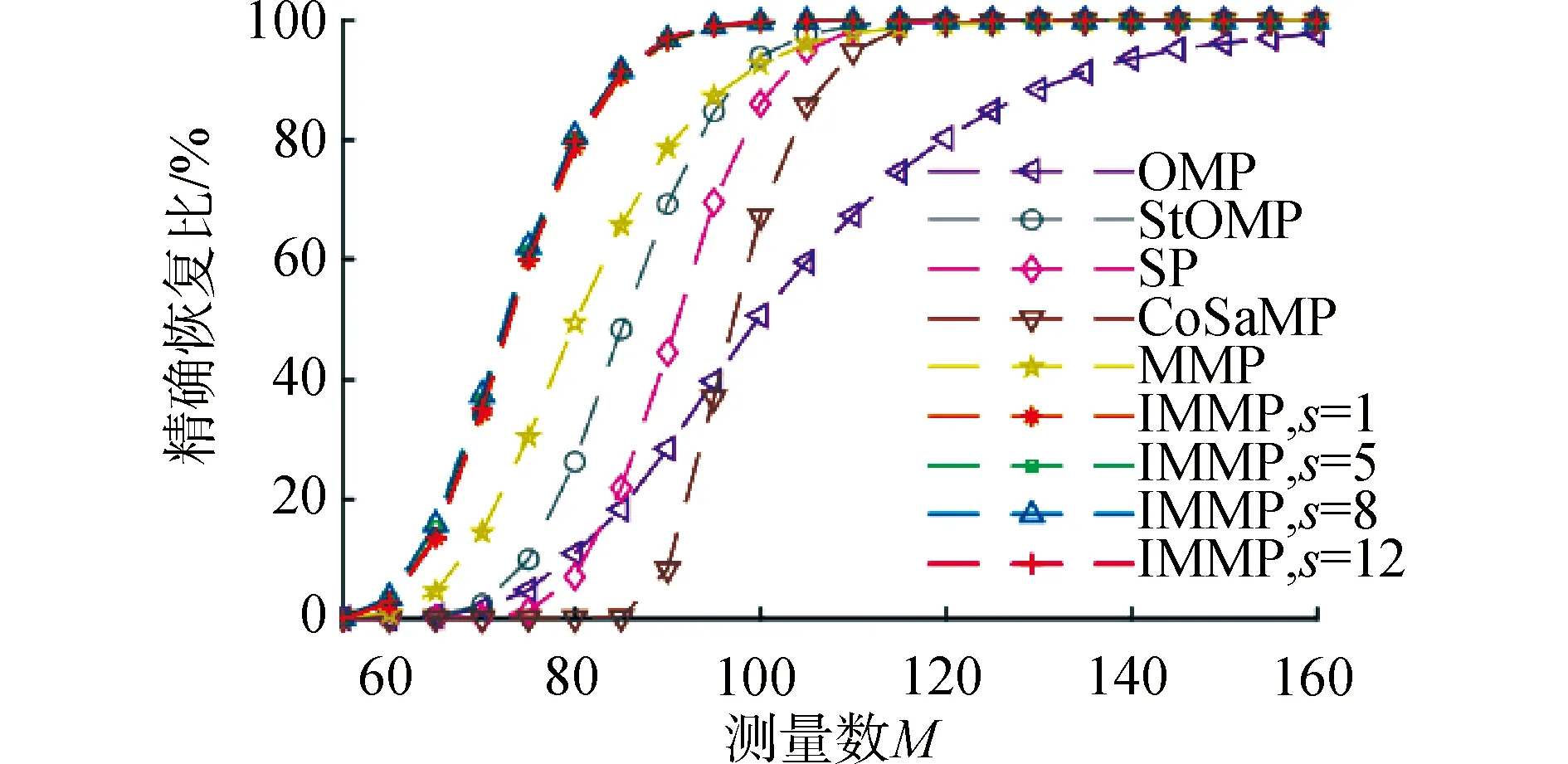
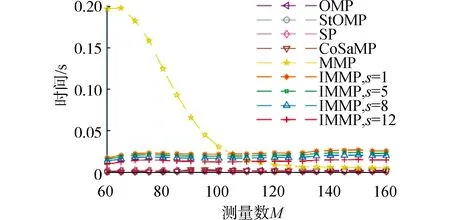
4) 如果j MMP算法改進了正交匹配追蹤算法支撐集非最優的不足,將正交匹配追蹤算法每個原子僅分支出一個原子改為分支出多個原子,其多樣化的搜索路徑使搜索范圍更廣,避免陷入局部最優解。理論上可以得到遠多于OMP算法的支撐集,大大提高了重構精度。但當遇到大規模數據時,MMP算法需要搜索大規模路徑,考慮實際應用需要對搜索路徑進行有效優化降低計算復雜度。 在實際應用中,重構信號的稀疏度一般是未知的,借鑒SAMP算法稀疏度自適應和SP算法回溯的思想,結合MMP算法的優點和不足,本文提出了IMMP算法。該算法對內積匹配準則進行改良,利用閾值法選擇支撐集,并采用變步長思想來逼近信號稀疏度,并對MMP算法的搜索路徑進行剪枝處理,在不影響重構質量的同時極大減少了運算時間,使之更具實用價值。下面主要從以下幾個方面對IMMP算法進行描述。 MMP等貪婪算法主要使用內積匹配準則度量測量矩陣與殘差值間的相關性強弱。傳統的內積匹配準則更多地是從方向上區分差異,而對絕對的數值不敏感,從而影響對相似原子的區分,使觀測矩陣中任意2個相近似的原子可能影響殘差信號的匹配過程。這種僅考慮向量維度方向上的相似性而沒考慮到各個維度量綱差異的不合理性會降低信號的重構質量。假設有任意向量a=(a1,a2,…,an)和向量b=(b1,b2,…,bn)。改良后的內積匹配準則公式為[21]: (11) (12) 從根節點迭代到第K個分支節點,其中每個節點代表不同的字典原子,當候選支撐集中選擇的原子數量等于稀疏度K時,認為此路徑搜索完成。根據原子選擇優先級的不同,將會得到不同的候選支撐集。取當前起始路徑l={1,2,…,LMAX},在后面每個路徑迭代過程中,一個最有希望的原子被添加到當前路徑中。當搜索路徑達到最大值LMAX或者完全確定最優路徑時終止迭代。圖1給出了該算法的樹搜索過程,其中LMAX=3,d=3,K=3。可以看到由C1=(1,1,1)確定的原子構成第1個支撐集,第2個支撐集則由C1=(2,1,1)確定的原子構成,直到選擇最佳的候選支撐集為止。 在當前支撐集迭代完成后,將與上一個支撐集執行回溯步驟用來選擇最佳的K個原子。在第2個候選支撐集{4,1,2}完成后,執行回溯細化沒有替換任何原子,第3個候選支撐集{6,3,4}回溯重新選擇原子后,支撐集更正為{6,2,4},提高了路徑搜索的精度。回溯雖然帶來了額外的計算負擔,但優化路徑大大降低了計算復雜度,提高了算法的重構精度。 稀疏度自適應算法設置的固定步長無法兼顧重構精度和重構效率,初始步長較小會降低算法重構效率,步長較大則會降低算法重構精度。采用兼顧兩者的變步長是一個不錯的方法。根據稀疏度估計的特點,改進算法稀疏度估計可以分為2個部分:1)初始階段大步長快速估計,2)完成階段小步長逐步逼近。 圖1 MMP和IMMP算法原理Fig.1 Schematic diagram of MMP and IMMP algorithms 文獻[22]研究表明,重構信號的殘差能量在2個相鄰階段中是遞減的,且隨著支撐集長度λ不斷逼近真實稀疏度K,殘差能量減小速度逐漸變緩趨于穩定。所以本文以相鄰階段重構信號的殘差能量作為步長變換的條件。當殘差能量小于等于‖rmin‖2時,步長切換更新稀疏度到下一階段,當殘差能量小于ε2時稀疏度估計過程完成。ε2是迭代停止閾值,在這里取ε2=10-6。 利用ax指數函數的變化規律來調整步長,初始階段步長取一個合適的初值s0,每次增加步長s=s0ax,支撐集長度λ=λ+s;其中a是固定常數,文獻[23]證明當a∈[0.3,0.5]時效果較好,x為當前候選支撐集迭代次數,「·?表示向上取整。當支撐集長度λ接近真實稀疏度K時,添加進支撐集的原子越來越少,直到支撐集長度λ=λ+1。采用此變步長方法可提高算法重構質量和計算效率。 根據上面對IMMP算法原理的描述,在下面分別詳細地給出了階段自適應估計稀疏度Search函數和IMMP算法的實現步驟: Search函數的實現步驟如下: 1) 輸入搜索序列Cl,殘差值r0,稀疏度λ,inputj={rj,Ωj,j}。 2) 如果j<λ或λ>length(Ωj),更新參數j=j+1,否則轉到步驟4)。 MMP-DF算法步驟如下: 本節使用一維信號模擬實驗,以信號精確重構比(exact reconstruction ratio, ERR)和重構時間作為算法重構性能的評價標準,其中當重構信號的殘差小于閾值ε1時,認為信號重構是成功的,本文取ε1=10-6。信號精確重構率反映了重構精度,其中ERR定義為準確恢復次數pn與總實驗次數psum的比值:ERR=pn/psum重構時間和迭代殘差反映了重構效率。仿真實驗使用Matlab(版本R2018b)在一臺裝配了Core i5-6400 @2.70GHz 處理器的計算機上進行。實驗中設置MMP和IMMP算法的最大迭代次數和子路徑數(LMAX,d)分別為(50, 6)和(10, 6)。選擇高斯隨機矩陣作為觀測矩陣,為避免隨機因素的干擾,每個算法都獨立重復進行了10 000次試驗且稀疏信號的非零位置都是隨機選擇的。 以典型的單路徑搜索算法OMP作為MMP算法中的一條搜索路徑中為例,分別使用內積準則和改進的內積準則來度量觀測矩陣原子和殘差信號的相關性,以便挑選最為匹配的原子。隨機生成稀疏度K=30,長度N=256的一維信號作為測試信號。比較在加入高斯噪聲后(SNR=15 dB),2種匹配準則下的殘差值隨不同迭代次數的變化情況,取對數表示的結果如圖2所示。 圖2 OMP不同迭代次數的殘差(K=30)Fig.2 Residual error of different iterations of OMP(K=30) 很明顯,隨著迭代次數增加,殘差值逐漸減小。同等條件下,可以從圖2看出改進的內積匹配準則的殘差值比內積準則更低,迭代過程中殘差值逼近零的速度更快。這充分說明改進的內積匹配準則不僅更有利于挑選最優匹配原子,降低誤選原子的概率,而且能夠加速完成迭代逼近,提高重構效率。 表1是當壓縮比M/N=[0.234 4,0.312 5,0.396 0]時,OMP算法應用2種不同原子匹配準則在不同高斯白噪聲等級(SNR=[0,5,10,15,20,25,30] dB)干擾下的平均重構信噪比,更進一步驗證了改進的內積匹配準則的性能。其中,重構信噪比公式為: (13) 表1 2種原子匹配準則的重構性能比較Table 1 Reconstruction performance comparisons of two atomic matching criterias 實驗表明應用改進的內積匹配準則在稀疏度和測量數2個方面都優于改進前的內積匹配準則。在相同壓縮比時,改進的內積匹配準則有更高的重構信噪比;在有相同的重構效果下,改進的內積匹配準則能適應更低的信噪比,抗干擾性能更優。改進的內積匹配準則從向量的夾角信息和長度數值信息2個方面更好地比較了向量間的相關性強弱,是一種更加合理有效的相關性度量準則。 本部分比較了IMMP算法與OMP、StOMP、SP、CoSaMP和MMP等5種稀疏信號重構算法的平均重構性能,同時也分析了在相同迭代次數下不同初始步長對IMMP算法性能影響。 圖3(a)給出了固定測量數M=100時,重構信號的ERR性能隨不同稀疏度K的變化曲線。從圖3(a)可以看出,本文提出的IMMP算法的ERR要高于傳統的重構算法,尤其當K>30時,IMMP算法的ERR明顯遠高于傳統算法。當K=40時,IMMP算法在初始步長s={1,5,8,12}時的ERR為86.59%、87.51%、88.12%和88.79%,而除了CoSaMP算法ERR為0外,OMP、StOMP、SP和MMP算法的ERR分別僅為6.99%、34.91%、4.99%和40.85%。 圖3(b)顯示了各種算法對應的CPU平均計算時間,客觀上可以比較算法的計算效率。MMP多路徑搜索算法計算時間隨著稀疏度K的增加呈現近似指數式增長,而OMP、StOMP、SP和CoSaMP算法的計算時間增加幅度不明顯。優化搜索路徑后的IMMP算法的計算時間較OMP、StOMP、SP和CoSaMP等單路徑搜索算法略有增加,但遠低于MMP算法。 圖3 不同稀疏度下IMMP算法性能驗證Fig.3 IMMP algorithm performance verification with different sparsity 圖4給出了稀疏度K=30,隨著測量數M增大時各種算法的重構成功率。容易由ERR曲線得到,除OMP算法外,其他算法在M>110時能取得極高的重構成功率,而IMMP算法在測量數M>90時也達到了相似的優良性能,所需測量數明顯減少。 圖4 不同測量數下的精確恢復比(K=30)Fig.4 The ERR for different measurements(K=30) 圖5說明了相應算法的平均計算時間,在M<110時,IMMP算法顯然比MMP算法花費更少的時間;而當M>110,IMMP算法由于要滿足迭代停止條件計算時間比其他算法要長,所以IMMP算法在壓縮比低的情況下更能體現出性能優勢。 圖5 CPU平均計算時間Fig.5 Average CPU time of computation 實驗結果表明,初始步長的大小對IMMP算法的重構性能影響也較為明顯。適當大的初始步長不僅能提高算法精確重構成功率,還能有效降低算法的計算時間,提高算法重構效率。IMMP算法具有良好的收斂速度和重構質量,表明優化后的精確的搜索策略可以加速搜索候選支撐集。 1)本文提出的IMMP算法可以盲稀疏度自適應估計,自適應選擇支撐集原子個數;而且改進的原子選擇方式能在高斯測量矩陣中更準確高效地挑選與殘差信號匹配的原子,并結合剪枝技術優化了MMP算法的路徑搜索,大大降低了算法計算時間。 2)MMP算法在迭代過程中采用支撐集原子回溯操作和指數變步長方法大大提高了信號重構精度。 3)仿真結果表明,該算法在不同測量數下性能有所差異,與傳統算法相比,得到的測量數較大時,算法計算時間有所增加,可適當減少迭代次數減少計算時間,而不會降低算法重構精度;在測量數較少時,該算法的信號重建精度高,運行時間短,更貼合實際工程應用。
2 改進的快速稀疏度自適應多路徑匹配追蹤算法
2.1 改進的內積匹配準則
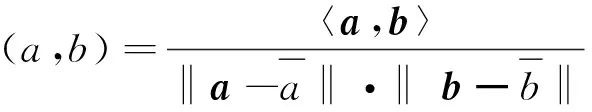
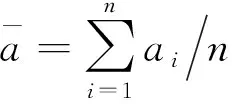
2.2 剪枝優化搜索路徑
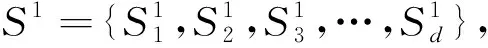
2.3 稀疏度自適應與指數變步長
2.4 算法步驟
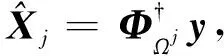
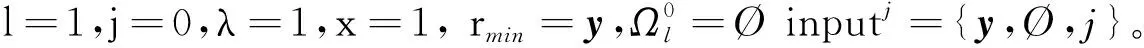
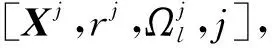
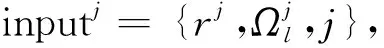
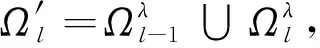
3 仿真驗證
3.1 改進的內積匹配準則的有效性驗證
3.2 算法性能分析
4 結論

