仿生尾緣對導管槳推進性能的影響

尚志強， 劉鵬， 王思琦， 劉然然， 劉福順， 王許潔

(1.中國海洋大學 山東省海洋工程重點實驗室，山東 青島 266100； 2.河口黃河河務局，山東 東營 257231)

導管螺旋槳又稱套筒螺旋槳，與普通螺旋槳不同的是外部多了一個套筒，導管的剖面分為折線型和機翼型。導管槳相比螺旋槳來說，能夠改善船尾伴流場，提高額外推力和推進效率。因此，導管槳在船舶上廣泛應用。

國內外對導管槳水動力性能方面做了大量的研究。呂曉軍等[1]研究了不同網格模型和湍流模型下導管槳的正車敞水性能曲線。胡健等[2-3]研究了導管槳內部流場數值特征，并探究了不同導管長度、葉稍間距和斜流對導管槳水動力性能的影響。謝永和等[4-5]研究了導管的長徑比、伸張系數和收縮系數以及導管型號對導管槳水動力性能的影響。Sanchez-Caja等[6]用計算流體力學方法分析了導管槳的水動力性能。Feiten等[7]等采用實驗的方法對導管槳進行了充分的研究。宋科等[8]探究了多導管螺旋槳的水動力性能。高慧等[9]探究了導管槳加上轂帽鰭后的節能性能。Caldas等[10]計算了不同舵分布下導管槳的操縱性以及其水動力性能。張正騫等[11]、孫瑜[12]等依據仿生學原理，研究了仿生導管槳的水動力性能。

本文以Ka4-5508+JD75導管槳為研究對象，利用Fluent對其水動力性能進行分析計算，將計算值與文獻[13]的實驗值對比，驗證這種復雜結構混合型網格劃分方法的可靠性。然后依據仿生學原理，以該槳為母型，利用三維建模軟件UG在導管后半段增加鋸齒突起，結合復雜結構混合型網格劃分方法在Gambit完成網格劃分，在Fluent軟件中實現對該仿生尾緣導管槳的水動力性能模擬，結合控制變量方法研究尾緣突起個數、尾緣長度和尾緣傾斜角度對仿生尾緣導管槳水動力性能的影響，并探究其水動力性能提升的機理。

1 數值方法與計算模型

1.1 數值計算方法

假設流體是不可壓縮的，本文采用RANS方程(雷諾平均方程)作為求解旋轉域的控制方程[14-15]，流場的連續性方程和動量方程可分別表示為：

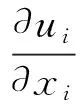
(1)

i,j=1,2,3

(2)

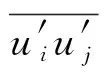
本文使用的SSTk-ω[16-17]模型，綜合了k-ω模型在近壁區計算的優點和k-ε模型在遠場計算的優點。與標準k-ω模型相比，SSTk-ω模型中增加了橫向耗散導數項，同時在湍流黏度定義中考慮了湍流剪切應力的輸運過程，模型中使用的湍流常數也有所不同。這些特點使得SSTk-ω模型的適用范圍更廣。

1.2 模型建立與網格劃分

本文研究采用的計算模型由JD75導管和Ka4-5508螺旋槳組成。螺旋槳直徑D=0.25 m，葉稍間隙1 mm，槳葉數4，盤面比為0.55，螺距P=0.2 m，相應螺距比P/D=0.8。圖1給出了Ka4-5508螺旋槳和JD75導管的模型以及改進后的仿生尾緣導管槳模型。借用三維建模軟件UG對JD75導管后半段進行改進，以導管后半段母線為基準線，改變仿生尾緣伸出距離為α，仿生尾緣傾斜角度為β，仿生尾緣突起個數為γ。

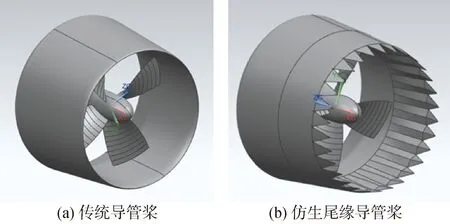
圖1 改進前后的導管槳模型Fig.1 Before and after improved of ducted propeller model

對于圖1(a)中的傳統導管槳，將導管槳的數據點導入Gambit中建模。由于導管內壁和螺旋槳葉稍間距很小，為了提高計算效率和保持相對較高的計算精度，并且基于復雜結構混合網格劃分方法,需對求解域進行更加細致地劃分。將求解域劃分為導管前、包含導管和槳的中部區域、導管后3個部分，然后又將包含導管和槳的中部區域劃分為含螺旋槳的單獨網格部分、含導管的網格部分和其余部分。為了后續劃分網格的需要，除螺旋槳所在域以外的部分分割成對稱結構體。如圖2所示，整個流場域大小一共61個體積，共220萬網格。計算域入口與槳盤面的距離為3D，計算域出口與槳盤面的距離為4D，計算域直徑為3D[18]。

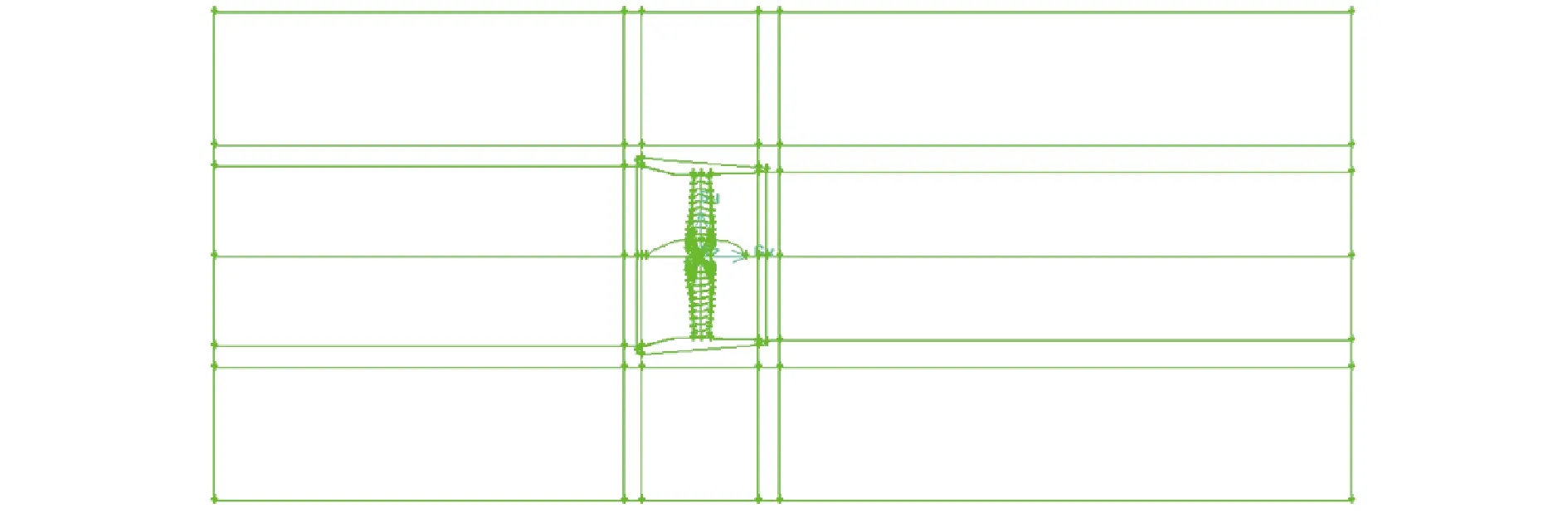
圖2 網格分塊劃分示意Fig.2 Schematic diagram of grid division

包含螺旋槳的域為動域，其余部分為靜域。動域的網格為非結構性四面體網格，如圖3(a)所示；對槳葉葉梢部分進行網格加密，導管前后緣采用Cooper的方式劃分體網格，由于導管內壁和螺旋槳葉稍間距很小，該部分采用結構網格并進行加密，其余部分均采用結構性網格，進流段和出流段適當降低網格數，如圖3(b)、(c)所示。這樣，在網格模型總節點數一定的情況下可以提高計算精度，還可以避免流場變化平緩區域計算資源的浪費。

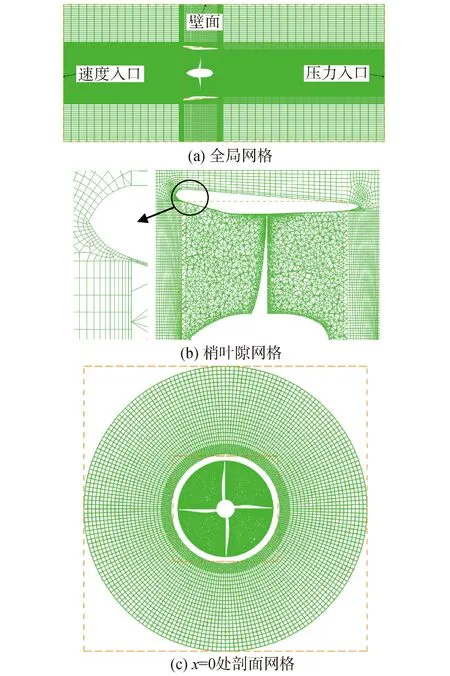
圖3 計算域的全局網格、梢葉隙網格及x=0處剖面網格Fig.3 The meshing of all domain, blade tip and section x=0

1.3 邊界條件及求解參數的設定

在螺旋槳敞水計算中，大域的入口邊界設置為速度入口；出口邊界設置為壓力出口；圓筒表面邊界設置為壁面；導管和螺旋槳表面設為無滑移、固壁邊界條件，如圖3(a)所示。螺旋槳所在的動域采用MRF (moving reference frame)方法，并繞x軸以600 r/min的速度旋轉，通過改變來流速度改變進速系數。使用Fluent軟件基于有限體積法求解RANS方程，湍流模型為SSTk-ω，采用三維單精度基于壓力隱式求解器，耦合方式采用SIMPLER算法，壓力項采用PRESTO方式，離散格式采用二階迎風格式，對導管槳的定常水動力性能進行計算，計算結果收斂后停止迭代。

2 數值驗證

分別取進速系數為0.1～0.7，螺旋槳轉速為600 r/min。通過Fluent軟件模擬其水動力性能，各系數定義表示為：

(3)

(4)

(5)

KT=KTp+KTd

(6)

螺旋槳推進性能為：

(7)

式中：KTp和KTd分別為螺旋槳和導管的推力系數；KQ為螺旋槳的轉矩系數；KT為導管槳的推力系數，Tp和Td分別為螺旋槳和導管的推力，N；Q為螺旋槳的轉矩，N·m；η為導管槳效率；J為進速系數；VA為來流速度，m/s；n為轉速，r/min；D為螺旋槳直徑，m；ρ為水的密度，kg/m3。

將計算值與實驗值相比較，結果如圖4所示。由圖4可知，計算值和實驗值曲線走向一致，呈現相同的變化規律，隨著進速系數的增加，推力系數和扭矩系數均減小，兩者誤差的絕對值也增大，效率誤差最大不超過3%，所對應的進速系數J=0.5。推力系數和扭矩系數的誤差較高的計算結果均出現在高進速系數情況下(J≥0.5)，而在低進速系數時，計算結果的誤差均低于8%。

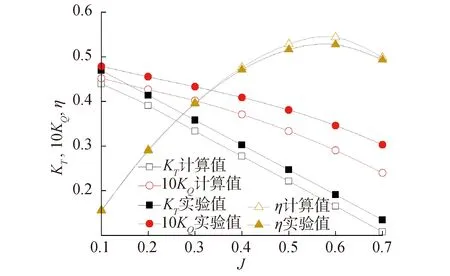
圖4 Ka4-5508+JD75導管槳敞水性能Fig.4 Open water performance of Ka4-5508+JD75 ducted propeller

存在誤差的原因主要由2個部分構成：一是數值模型和實驗模型存在出入，在Gambit中建模時，生成的槳葉和槳轂較為簡單粗糙，這也就導致了與實驗模型存在一定誤差。同時數值計算過程中離散方程的截斷誤差以及舍入誤差也是不容忽略的，實驗設備以及實驗條件的設置也能夠引起誤差。二是利用Fluent軟件模擬螺旋槳的敞水性能是在理想狀態下進行的，這在現實中是不可能達到的，實驗中的水面興波以及水池壁面等因素的影響并沒有考慮到。

總的來說，利用以上提出的數值模擬方法模擬導管槳的水動力性能是可行的，滿足模擬精度要求。

3 仿生尾緣導管槳水動力特性及影響因素分析

采用上文提出的基于復雜結構混合型網格劃分方法，選取α=0.2L(L為導管長度)，β=6°，γ=30作為仿生尾緣導管槳的初始參數，采用控制變量的方法來探究參數對仿生尾緣導管槳水動力性能的影響。

3.1 尾緣突起個數

改變尾緣突起個數γ分別為20、24、30、36，固定α=0.2L，β=6°，探究尾緣突起個數的改變對導管槳推力系數、扭矩系數和效率的影響，如圖5所示，圖中“Duct”表示尾緣未改進導管槳的相應性能曲線。

從圖5(a)中可以看出改變仿生尾緣突起個數后的推力系數較傳統導管槳有較大提升，隨著進速系數提高，推力系數增長速度增大，最大值出現在γ=20、J=0.7時為25%。尾緣突起個數的改變對推進系數的影響很小，整體上看隨著尾緣突起個數的增加，推力系數略微減小。

從圖5(b)中可以看出改變仿生尾緣突起個數后的扭矩系數較傳統導管槳同樣有較大提升，隨著進速系數提高，扭矩系數增長速度增大，但增長的幅度較推力系數小，最大值出現在γ=20、J=0.7時為19%。從整體上看，隨著尾緣突起個數的增加，扭矩減小，低進速系數下扭矩減小的幅度相比較于高進速系數更大。

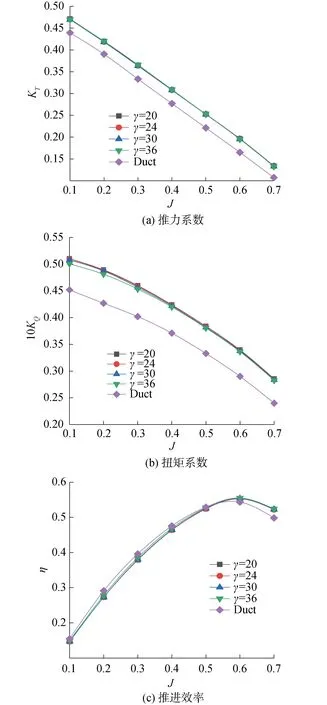
圖5 不同尾緣突起個數的敞水性能曲線Fig.5 Open water performance of different number of trailing edge protuberances

從圖5(c)中可以看出低于J=0.5時，傳統導管槳的效率高于仿生尾緣導管槳的效率，隨著進速系數增加，仿生尾緣導管槳與傳統導管槳效率的差值減小。大于J=0.5情況下，仿生尾緣導管槳效率高于傳統導管槳，最大值為5.16%出現在γ=36、J=0.7時。當進速系數J>0.5時，效率隨著突起個數的增加而增加。

由此得出結論：突起個數的變化對推力系數和扭矩系數影響不大，當J>0.5時仿生尾緣導管槳的效率高于普通導管槳的效率，J<0.5時，反而低于普通導管槳的效率，起到不利的影響。

3.2 尾緣長度

改變尾緣長度α分別為0.1L、0.15L、0.2L、0.25L、0.3L，固定β=6°，γ=30，探究尾緣長度的改變對導管槳推力系數、扭矩系數和效率的影響，如圖6。

從圖6(a)中可以看出改變仿生尾緣長度后的推力系數較傳統導管槳有較大提升，隨著進速系數提高，推力系數增長速度增大，最大值出在α=0.3L、J=0.7時為25.57%。尾緣長度的改變對推進系數的影響很小，整體上看隨著尾緣長度的增加，推力系數增加的幅度很小。

從圖6(b)中可以看出改變仿生尾緣長度后的扭矩系數較傳統導管槳同樣有較大提升，隨著進速系數提高，扭矩系數增長速度增大，不過增加的幅度較推力系數小，最大值出在α=0.3L、J=0.7時為18.9%。從整體上看，隨著尾緣長度的增加，扭矩增加幅度很小。

從圖6(c)中可以看出低于J=0.5時，傳統導管槳的效率高于仿生尾緣導管槳的效率，隨著進速系數增加，仿生尾緣導管槳與傳統導管槳效率的差值減小。大于J=0.5情況下，仿生尾緣導管槳效率高于傳統導管槳，最大值為5.6%出現在α=0.3L、J=0.7時。在進速系數J>0.5情況下，隨著尾緣長度的增加，效率也小幅度增加。

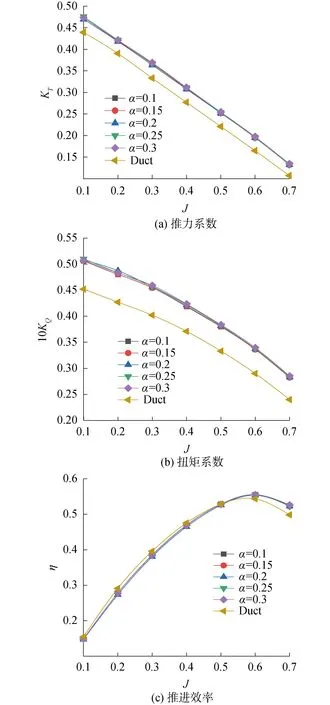
圖6 不同尾緣長度的敞水性能曲線Fig.6 Open water performance of different trailing edge lengths

由此得出結論：尾緣長度的變化對推力系數和扭矩系數影響不大，在J>0.5時，能夠提高效率，J<0.5時，低于普通導管槳的效率。

3.3 尾緣傾斜角度

改變尾緣傾斜角度β分別為2°、4°、6°、8°、10°，固定α=0.2L，γ=30，探究尾緣傾斜角度對導管槳推力系數、扭矩系數和效率的影響，如圖7所示。

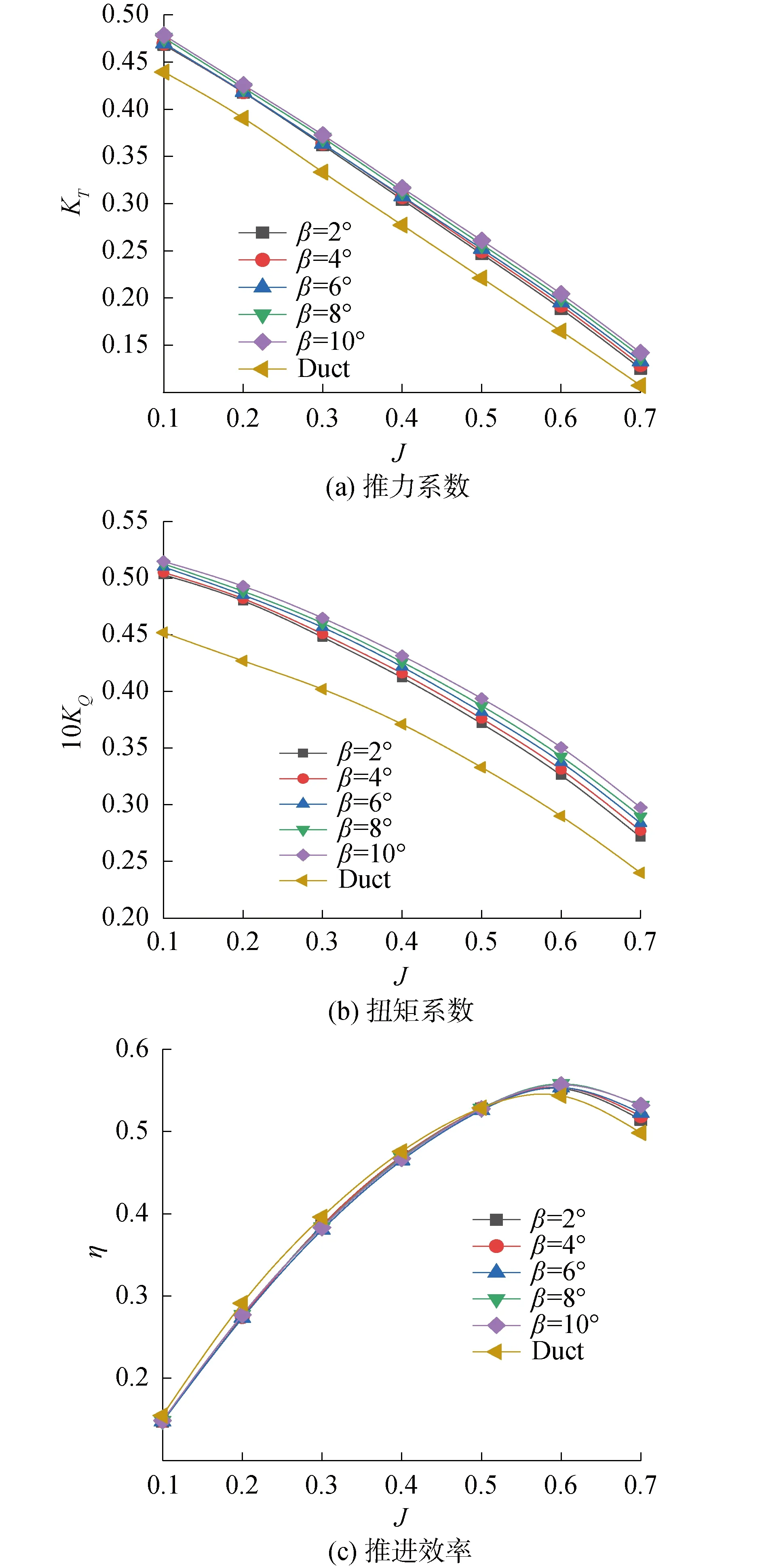
圖7 不同尾緣傾斜角度的敞水性能曲線Fig.7 Open water performance of different trailing edge inclination angles

如圖7(a)所示，改變仿生尾緣傾斜角度后的導管槳的推力系數較傳統導管槳有較大提升，隨著進速系數的增加，推力系數增長速度增大，最大值出在β=10°、J=0.7時為32.4%。隨著尾緣傾斜角度的增加，推力系數增加，增加的幅度比圖5(a)和圖6(a)中的幅度大。

如圖7(b)所示，改變仿生尾緣傾斜角度后的扭矩系數較傳統導管槳同樣有較大提升，隨著進速系數提高，扭矩系數增長速度在增大，最大值出在β=10°、J=0.7時為24%。隨著尾緣傾斜角度的增加，可以明顯地看出扭矩系數在增加，增加的幅度較圖5(b)和圖6(b)中更明顯。

如圖7(c)所示，低于J=0.5時，傳統導管槳的效率高于仿生尾緣導管槳的效率，隨著進速系數增加，仿生尾緣導管槳與傳統導管槳效率的差值在減小。大于J=0.5情況下，仿生尾緣導管槳效率高于傳統導管槳，最大值為6.7%出現在β=10°、J=0.7時。在進速系數J>0.5情況下，隨著尾緣長度的增加，效率在增加。

由此得出結論：尾緣傾斜角度的變化對推力系數和扭矩系數的影響比較明顯，隨著傾斜角度增加，推力系數和扭矩系數也在增加，對效率的影響與3.1節和3.2節中相同，不過效率增加速度較前2種工況更快。當角度繼續增加時，水流沖擊仿生尾緣的載荷增大，相應齒根應力的增加可能導致螺旋槳的損壞，同時高流速下易產生空泡影響仿生尾緣水動力性能。因此，目前只在尾緣傾斜角度的有限范圍內進行計算。后續研究中，將把推進性能、結構強度以及空泡性能綜合考慮進行分析。

3.4 槳葉壓力分布對比

圖8是J=0.7、來流速度1.75 m/s、螺旋槳轉速600 r/min時的槳葉壓力圖。對比分析改進前后的槳葉壓力分布圖，得到推力增加的機理，圖8是改進前和改進后(α=0.2L、β=10°、γ=30個)的槳葉壓力分布圖。

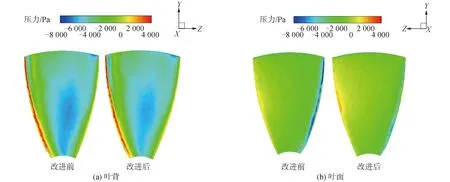
圖8 J=0.7 時導管改進前后槳葉壓力分布對比Fig.8 Comparison of blade pressure distribution before and after duct improvement at J=0.7

觀察圖8可以看到導管改進后對葉背壓力分布影響較小，仔細對比觀察后發現導管改進后的葉背壓力分布更均勻，中心處的低壓區明顯減小。相比之下，導管改進后的葉面隨邊的高壓區擴大，導邊的低壓區減小，槳葉上的壓力分布變化導致推力增大。另外通過壓力分布對比，導管改造后低壓區減少，最低壓力值提升，這樣有利于減緩空泡的發生和螺旋槳運行的噪聲。

3.5 流場x軸方向速度分布

圖9是J=0.4、來流速度1.0 m/s、螺旋槳轉速600 r/min時的槳葉壓力圖。

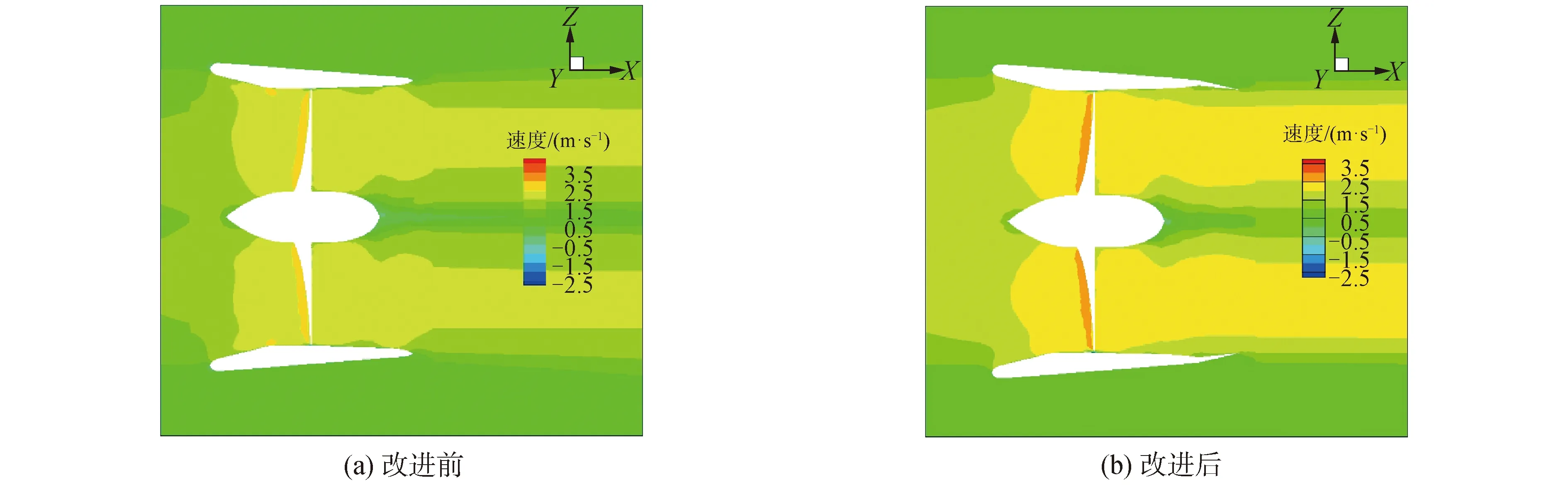
圖9 J=0.4時導管改進前后X軸速度分布對比圖Fig.9 Comparison of X-axis velocity distribution before and after improvement of duct at J=0.4

對比改進前后x軸速度分布對比圖發現：導管改進前，x軸方向的速度分布數值絕大多數在2.0～2.5 m/s；而導管改進后，x軸方向的速度分布數值絕大多數在2.5～3.0 m/s且速度分布面積擴大。因此，導管改進后，流場得到改善，導管槳的推力相應增加。

4 結論

1)通過應用計算流體力學中的SSTk-ω模型和旋轉坐標系方法，基于復雜結構混合型網格劃分方法，在Fluent軟件中實現對導管槳的數值模擬，對比計算值和實驗值，驗證這種混合型網格劃分方法的可靠性。

2)通過分析導管槳改進前后的水動力性能曲線和壓力、速度分布圖，發現：該仿生尾緣導管槳相比傳統導管槳來說，推力系數和扭矩系數均有較大提升，效率在高進速系數有提升；改進后的葉背壓力分布更加均勻，導管改造后低壓區減少，最低壓力值提高，有利于減緩空泡的發生和螺旋槳運行的噪聲；導管改進后，x軸方向的速度增加，流場得到改善，導管槳的推力得到增加。

3)該仿生尾緣導管槳更適用于高進速系數的船舶，能夠提高效率起到有利影響，符合綠色船舶的發展趨勢，低進速的船舶不建議采用此改進方式。

在接下來的研究中，可以選擇最優模型開展敞水實驗，以及針對噪聲和不同導管槳模型開展研究。