LOM薄木層積熱壓過程中溫度實時模擬模型構建*

楊春梅 寧禮佳 劉清偉 繆 騫 馬 巖 劉九慶

(1.東北林業大學機電工程學院 哈爾濱 150040； 2.哈爾濱工業大學航天學院 哈爾濱 150001)

近年來，結合數字化設計、制造技術，先進材料技術以及激光、電子束等高能束流工藝的3D打印增材制造技術受到熱捧，被認為是可能改變制造行業的一次新的技術革命(盧秉恒等， 2015； 王強等， 2018)。LOM(laminated object manufacturing)技術，也稱分層實體制造，是3D打印增材制造技術的重要分支之一，也是一種快速層壓成型工藝(馮明智， 2013； 黃彬等， 2012； 于利等， 2012)，將LOM技術引進木材加工領域，在不損害木制品細胞組織形態、保證木制品紋理美觀的前提下實現木制品成型，可解決我國傳統木制品加工周期長、更新換代緩慢和加工效率低等問題，為木制品加工行業提供了新的思路(Zhouetal.， 2015)。基于LOM技術的薄木層積過程中，熱壓溫度是保證薄木良好黏合的基礎，熱壓溫度過高，可能灼傷薄木表面，也可能使膠層過度固化，導致膠層變脆和熱解； 熱壓溫度過低，膠層達不到固化溫度，產品質量不滿足使用要求(Younsietal.， 2007； Asgharetal.， 2018)。在木材傳熱傳質研究(陶文銓， 2001)基礎上，Ahn等(2012)提出一種基于LOM的薄木傳熱傳質模型，分析了熱傳導時熱壓壓力對零件的影響。Sonmez等(1998)對層壓過程中的熱力學行為進行數值分析，通過建立模型探討了工藝參數與層合板內部溫度和應力分布的關系。Liao等(2006)提出加熱分壓分離系統，建立熱模型，采用有限元軟件ANSYS進行數值求解，研究了系統的傳熱問題。

木材具有各向異性，同時細胞腔和細胞間隙之間有大量孔隙，這使其在LOM薄木層積熱壓過程中存在一些困難，如薄木容易剝離黏合層、零件內會產生氣泡，且熱壓過程參數難以控制，零件翹曲引起變形，零件可能因過熱而燒毀或因溫度不足而發生毀壞等(程偉等， 2007； 余養倫等， 2007)。鑒于此，本研究結合LOM工藝加工流程，對微米薄木傳熱過程進行簡化，以木材傳熱理論為基礎，建立模型的控制方程和邊界方程，采用向前差分法對控制方程和邊界條件進行離散，利用MATLAB軟件實時模擬薄木層積熱壓過程中零件內部的溫度場，觀察溫度場變化，對不同深度層的溫度分布曲線進行分析，解釋層積熱壓過程中溫度隨層數變化的規律，探討熱壓工藝參數與溫度場分布梯度的關系，以期為滿足成型零件膠合質量與加工精度需求提供參考。

1 工藝分析

LOM作為一種快速層壓成型工藝，其成型系統主要由原材料粘貼、熱壓、激光掃描和落料幾部分組成，工作原理如圖1所示。首先將涂有熱熔膠的紙層通過熱壓機構與原有紙層黏結，然后激光束按照截面輪廓數據對當前紙層進行掃描切割，完成輪廓成型，同時將非輪廓部分切成網格狀，通過落料機構對其進行清理，反復迭代，直至零件成型(張健等， 2008； 于冬梅， 2011； 周六剛， 2004)。

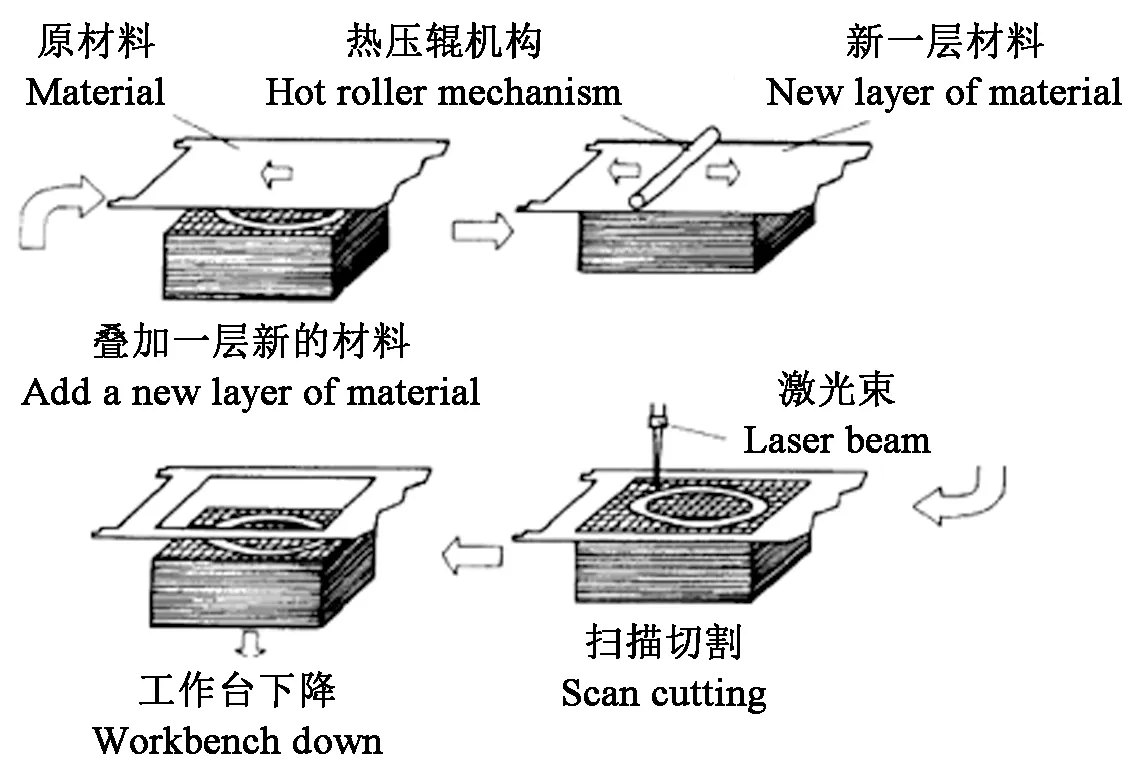
圖1 LOM工藝流程

通過分析現有LOM工藝成型原理，調整LOM工藝加工工序，解決目前LOM成型時因激光切割過程中激光光斑熱影響區導致熱溶膠提前固化的問題，提高零件的力學性能。改進后木制品層積成型設備的結構示意如圖2所示。

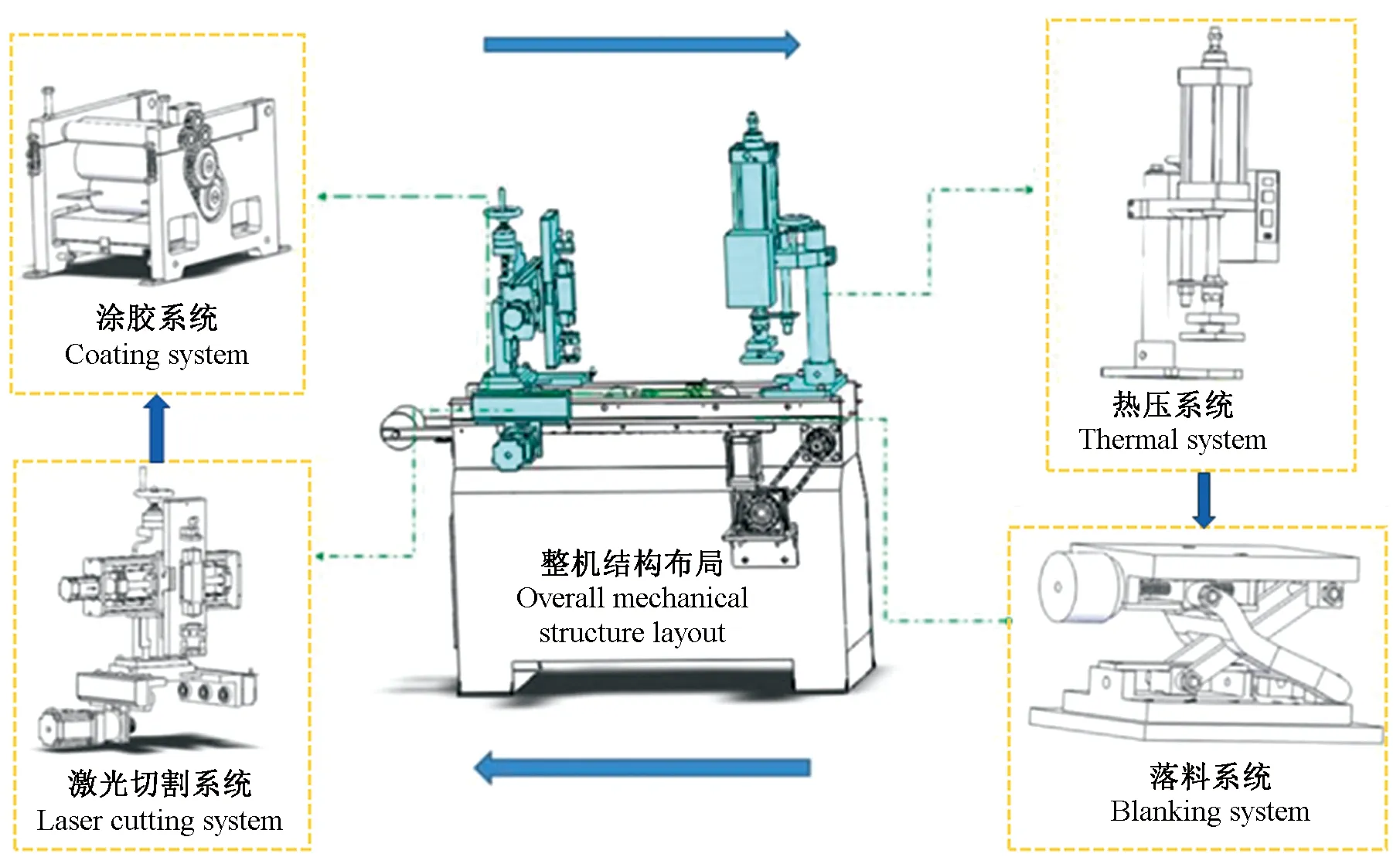
圖2 木制品層積成型設備結構示意

木制品層積成型設備主要由激光切割系統、涂膠系統、熱壓系統、落料系統等組成。在工作過程中，首先進料滾筒通過鏈傳動將單層薄木運至工作臺上，激光系統對單層薄木進行切割，切割后的二維輪廓以及廢料通過鏈傳動傳遞至涂膠系統，涂膠后經鏈傳動運輸至熱壓系統，完成零件的熱壓成型； 與此同時，落料系統通過升降臺對已經成型的零件進行落料處理，如此反復迭代，直至零件加工完成。

2 層積熱壓模型構建

LOM成型過程中，熱壓是一道非常重要的工序，對零件上表面進行熱壓時，零件內部將產生非穩定、不均勻的溫度分布，在溫度場作用下，零件內部將產生熱應力，熱應力不斷累積會導致零件翹曲變形，影響零件的精度。因此，需要控制熱壓板加熱時的熱壓溫度，以提高薄木的黏結質量。

2.1 模型基本假設

本研究采用一種動態模型實時模擬薄木層積熱壓過程中的溫度場變化，通過實時調整熱壓工藝參數使其具有穩定的溫度梯度。為簡化模型，做出以下假設： 1) 將層積疊加后的木制品看作一個各向異性但分布均勻的連續體，分析過程中忽略薄木和熱熔膠熱物理力學性能上的差異性； 2) 激光切割對溫度場的影響忽略不計； 3) 薄木在長度和寬度方向上受熱均勻，零件邊緣存在的溫度梯度忽略不計，單層微米薄木厚度為0.01 mm，側面散熱忽略不計，層積熱壓過程的三維非穩態導熱問題簡化成一維非穩態傳熱問題。

2.2 模型構建

結合LOM工藝流程，按照熱壓板工作過程，將模型分為熱壓板工作狀態和非工作狀態分別探討。

2.2.1 熱壓板工作狀態 1) 控制方程 圖3所示為熱壓板工作時的主視圖，選擇零件左下角為坐標系原點，根據木材傳熱學原理，由能量守恒定律可得控制方程為：

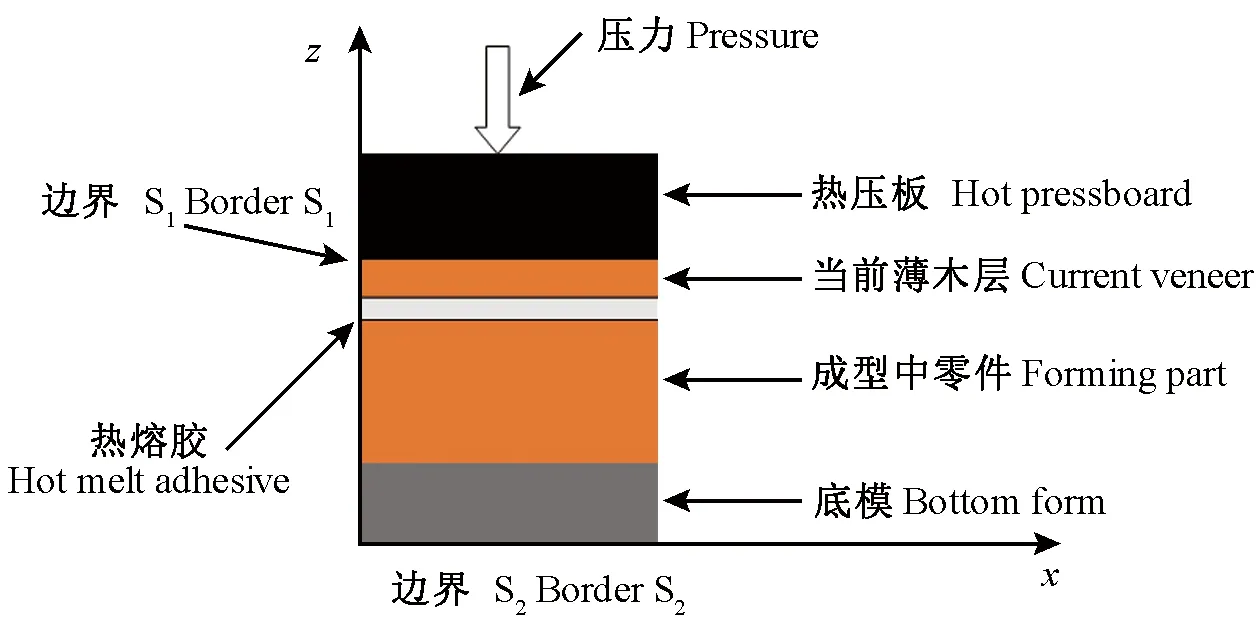
圖3 熱壓板工作時模型

(1)

式中：α表示木材在垂直方向上的傳熱系數。

2) 邊界條件 薄木和熱壓板接觸的邊界用S1表示，邊界的對流條件如下：

(2)

式中：kt表示薄木的傳熱系數；Tb表示熱壓板的溫度；hb表示熱壓板的傳遞系數。

底模下表面和空氣接觸的邊界用S2表示，邊界的對流條件如下：

(3)

式中：km表示底模的傳熱系數；h3表示底模和空氣的對流換熱系數；Tc表示成型室內溫度。

2.2.2 熱壓板非工作狀態 此時薄木黏結結束，新層與舊層之間完全黏合，熱壓機停止工作，其模型如4所示。薄木層積過程中，整體傳熱控制方程不變，由于熱壓機離開薄木表面，所以S1的邊界條件變為一個自然的散熱過程，S2邊界不變，其邊界條件如下：

(4)

式中：h4表示薄木和空氣的對流換熱系數。

3 模型離散化

3.1 模型離散化原理

模型的控制方程為一維非穩態熱傳導方程，具有復雜的級數解，且在解決實際物理問題時邊界條件復雜多樣，不便于數值求解，因此本研究采用有限差分方法對其進行求解。對求解區域進行離散化處理，如圖5所示。

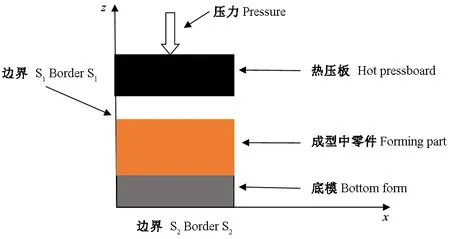
圖4 熱壓板不工作時模型

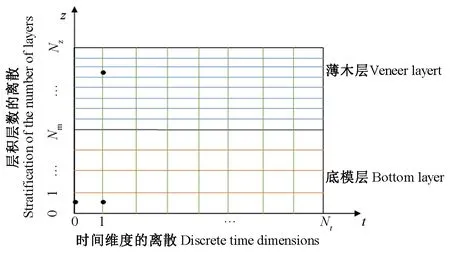
圖5 模型單元劃分

采用上述方法劃分求解區域，可以保證除了邊界點外每個節點都控制在一個薄木層上，有利于邊界條件表達，同時網格結構可以清晰表達研究區域的變化情況。利用該方法將加工區域進行離散，得到一系列數據點(ti，zi)，其中：

ti=ihti=1, 2, 3, …,Nt；

(5)

(6)

式中：Nt表示沿著t方向劃分的網格數；Nm表示z方向上底模的網格數；Nz表示z方向上薄木層和底模的總網格數；ht表示時間方向上的步長；hz1表示底模的步長；hz2表示薄木層的步長，取值為薄木層厚度。

3.2 模型離散化

為了提高MATLAB的運行速度，減少計算過程中的工作量，采用向前差分法，得到差分方程如下。

根據差分原理，薄木層的一維熱傳導方程寫成差分形式為：

(7)

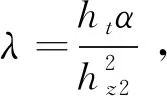
T(i,k+1)=λT(i+1,k)+(1-2λ)T(i,k)+λT(i-1,k)。

(8)

式中：i=0, 1, 2, 3,…,Nt；k=0, 1, 2, 3, …,Nz+1。

將上式寫成遞推公式表達為：

(9)

將其轉化成矩陣形式表達為：

(10)

同理可得底模節點的離散方程(由于文章篇幅所限，關于底模離散方程只給出離散結果，具體推導過程等相關內容不再列出)：

(11)

對邊界S1上的點進行離散，對于邊界S1上的點T=T(i,k+1)，根據第三類邊界條件，由能量守恒定律可得：

(12)

經整理得：

(13)

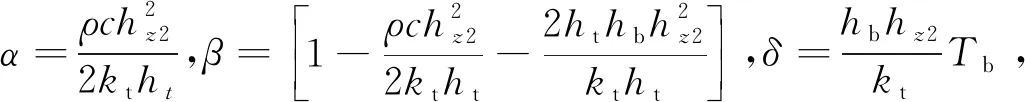
T(i,k+1)=αT(i+1,k)+βT(i,k)+δ。

(14)

將上式寫成遞推公式表達為：

(15)

將式(15)轉化為矩陣形式表達為：

(16)

式中：E表示單位矩陣。

同理可將式(3)和(4)的邊界條件進行離散(由于重復，具體推導過程不再列出，只給出離散結果)，式(3)的離散結果如式(17)所示，式(4)的離散結果如式(18)所示：

(17)

(18)

4 模型求解與分析

4.1 模型求解

針對以上模型，應用MATLAB軟件對其編程，求解每個節點不同時刻的溫度。每鋪上一層為一個循環，如此反復疊加，直至整個零件加工結束(陸君安， 2001； 王潔等， 2010； 徐凱等， 2016)。為了更好表達層積熱壓過程中熱壓溫度、熱壓時間以及層數的數學關系，以層積15層為例，對層積件的溫度變化進行分析，仿真模擬過程中所需要工藝參數如表1所示，結果如圖6所示。

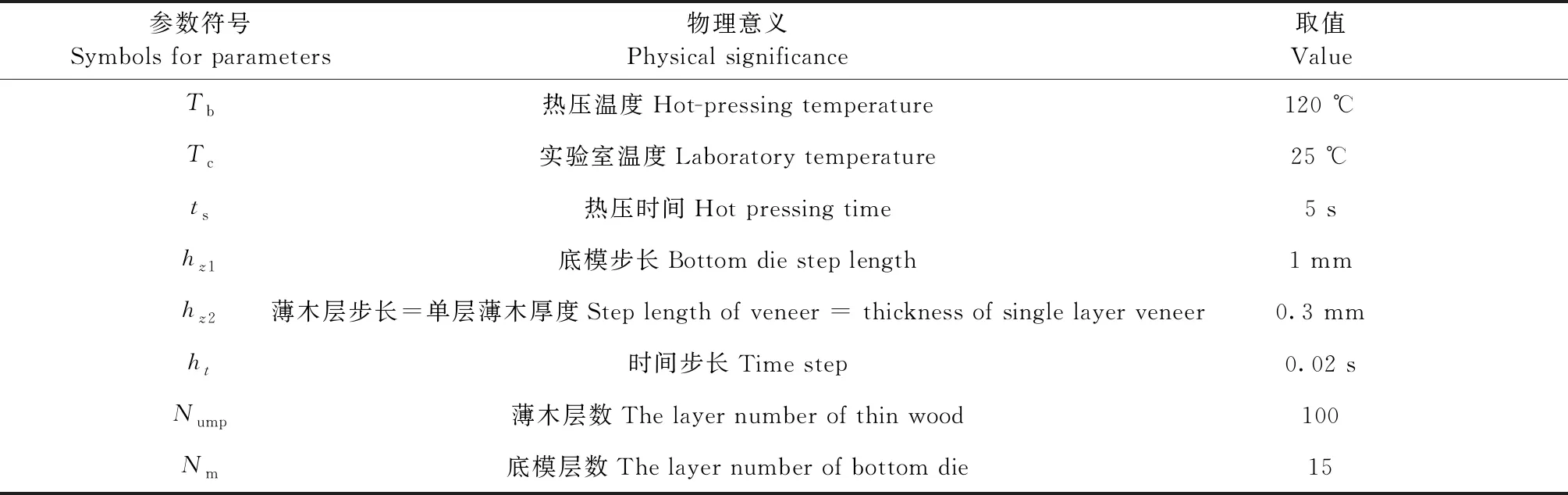
表1 工藝參數

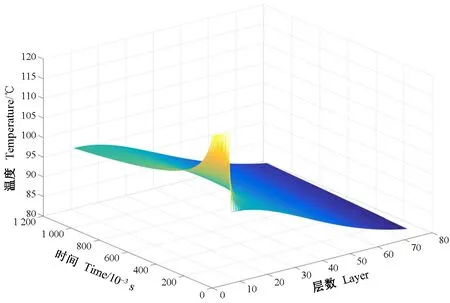
圖6 薄木層積過程溫度場實時模擬仿真

基于LOM技術的微米薄木成型過程中，設定不同工藝參數均可實現對零件各層溫度變化的實時模擬，能夠求解零件各層每一時刻的溫度分布。探索LOM技術微米薄木層積過程中溫度的時刻變化不僅有利于控制零件溫度場變化，改善零件內部產生熱應力引起的翹曲變形，防止發生錯層漏層現象，提升薄木層黏接質量，而且有助于對熱壓過程中的溫度進行動態調整。在LOM微米薄木層積過程中，影響溫度場的工藝參數很多，為了實現對溫度場的精確控制，需要對工藝參數影響溫度場的變化規律進行研究。

4.2 模型分析

為了研究薄木層數量對溫度場的影響規律，在不同時間下，利用仿真數據將靠近熱壓板和遠離熱壓板的各層溫度分布繪制成二維折線圖，如圖7所示。

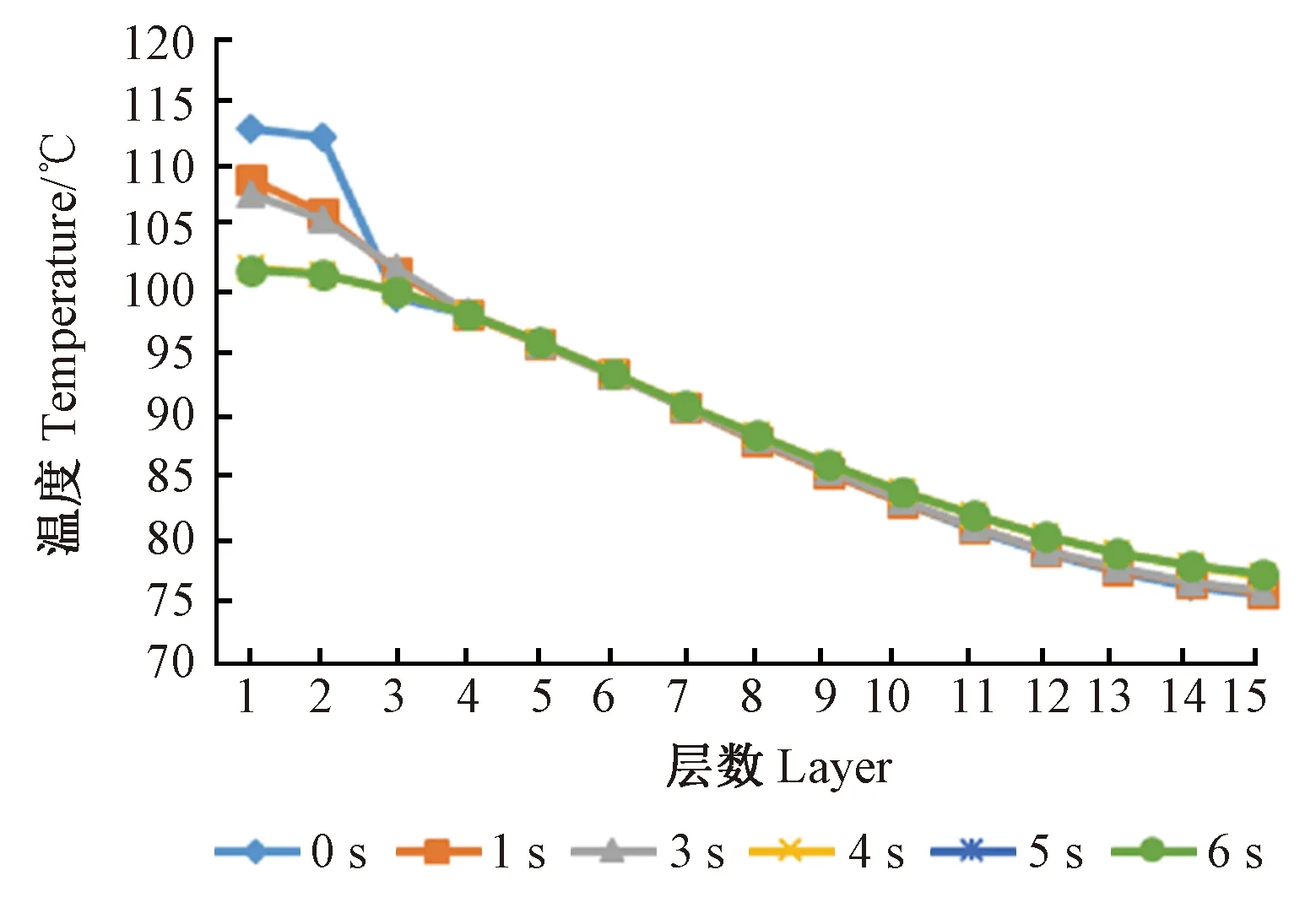
圖7 不同時間溫度隨層數的變化規律

隨著薄木層積厚度增加，熱壓板對薄木層溫度的影響不斷減弱，與熱壓板接觸附近的薄木層，其層內最高溫度隨著深度增加迅速下降，而一定深度以下的薄木層，層與層之間的變化不顯著。靠近熱壓板的表面層，接觸熱壓板的薄木層溫度變化顯著。這是因為當熱壓板工作時，薄木層與熱壓板之間產生強烈的對流換熱，薄木層溫度上升。熱壓板不工作時，薄木層與空氣進行換熱，薄木層溫度下降； 但是在一定深度以下的薄木層，溫度變化幅度很小，同一層內溫度分布比較均勻。

4.3 試驗分析

試驗于東北秋季進行，室外溫度20 ℃，空氣相對濕度15%，選用0.1 mm厚櫻桃木(Prunus)，氣干密度為0.85 g·m-3，含水率為10%，幅面為100 mm×100 mm，按順紋方向組坯。熱壓機選用深圳多禾科技有限公司生產的氣動熱壓機，試驗過程中熱壓溫度為120 ℃，將熱電偶導線一端置于板坯中心處，另一端與杭州聯測自動化技術有限公司生產的SIN-R6000C測溫儀相連，測試每層板坯的熱壓升溫曲線，每隔1 s讀取1次測溫數據，測試第1 s、第3 s、第5 s的溫度，每組試驗重復2次，取平均值得出試驗數據與模擬數據如表2所示。

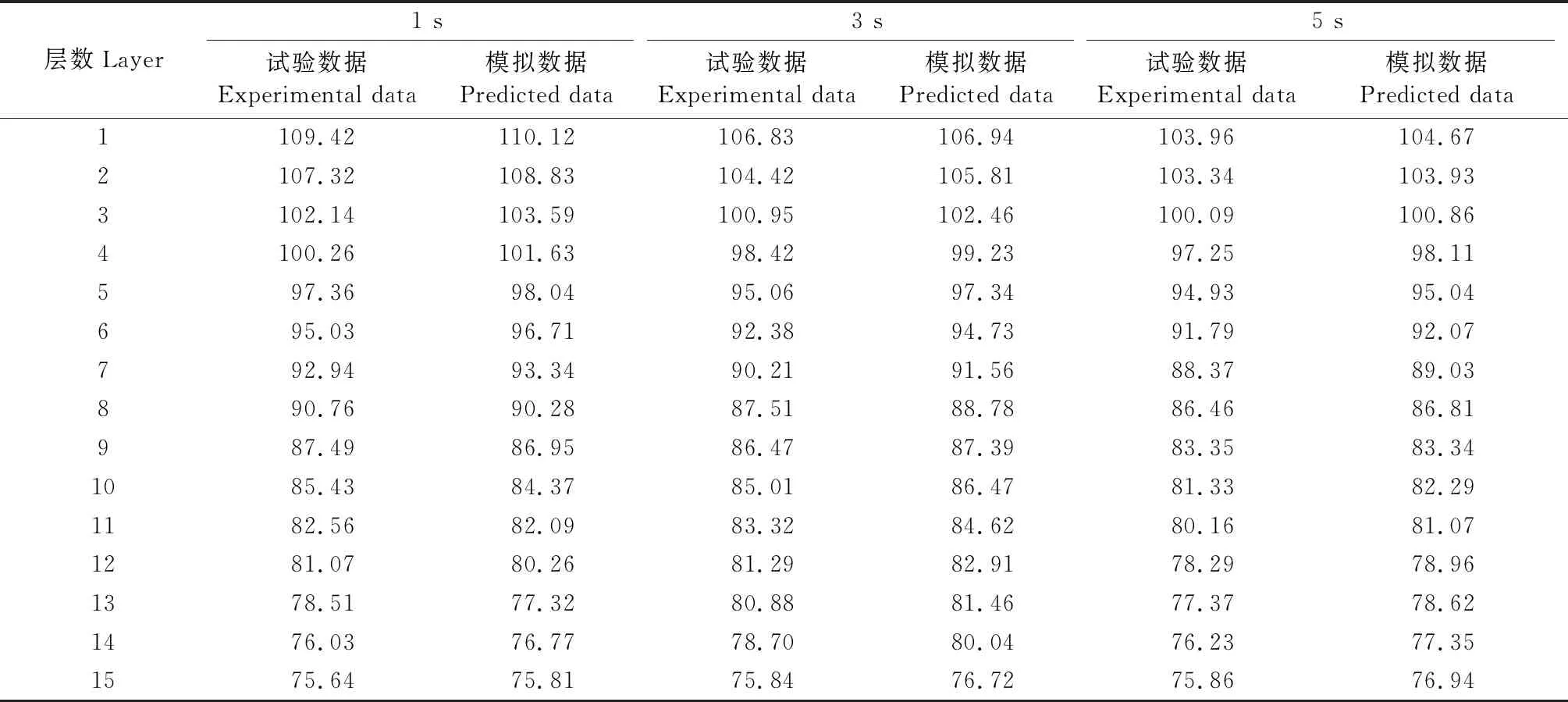
表2 各層溫度實測值

試驗中部分數據在同等層數下出現5 s時的溫度低于3 s時的情況，這是木材和水分對熱量的吸收作用以及層積過程中熱量從側面流失導致。將試驗結果與模型結果進行對比，得到統計數據如圖8所示。

利用擬合優度(R2)驗證模擬數據與試驗數據之間的擬合程度，其表達式如下：

(19)

式中：SST=SSR+SSE為總平方和；SSR為回歸平方和；SSE為殘差平方和。

將上述模擬數據與試驗數據導入MATLAB軟件，在cftool命令窗口求得擬合函數，擬合優度R2=0.996 3，模擬數據與試驗數據擬合優度較高，模型可以較為準確預測熱壓時的溫度，對熱壓工藝有較強指導作用。

5 結論

1) 以木材傳熱理論為基礎，根據能量守恒定律，建立LOM薄木層積熱壓過程的傳熱控制方程和邊界方程，通過基本假設簡化模型，將層積熱壓過程的三維非穩態導熱問題簡化為一維非穩態傳熱問題，降低了模型求解難度。按照熱壓板工作過程，將模型分為熱壓板工作狀態和非工作狀態，提高了模型解的精確性。采用向前差分法對控制方程和邊界條件進行離散，提高了程序運行速度，依托MATLAB對模型進行求解，繪制出時間-層數-溫度三維圖，使結果更清晰化。

2) 通過MATLAB對模型進行求解，結合溫度場，根據仿真求解數據繪制二維折線圖顯示出： 在靠近熱壓板的表面層，接觸熱壓板的薄木層溫度變化顯著，熱壓板對薄木層溫度的影響隨著薄木層深度增加不斷減弱； 在一定深度下，溫度變化幅度很小，同一層內溫度分布比較均勻。

3) 模型中模擬數據與試驗數據擬合優度較高，模型可以很好預測熱壓過程中各層板材溫度，對LOM單木層積熱壓工藝具有較強指導作用。