鈉原子s、p能級量子缺的普通物理實驗粗測法

丁又也，張三軍，尹亞玲

（華東師范大學 物理與電子科學學學院 物理實驗教學中心，上海 200241）

“分光計的調節與三棱鏡折射率的測量”是高校普通物理實驗中的經典實驗，該實驗著重訓練學生學會分光計的調整與使用，以及對基于實驗得到的數據進行基礎的處理，從而理性認識折射率與波長的關系.常見的分光計實驗的分光器具為三棱鏡，光源為低壓汞燈光源.低壓汞燈接近白色，各譜線強度相近，通過三棱鏡色散后可以清晰地看到黃色、綠色、紫色的譜線.在該實驗中，學生觀察汞燈不同顏色的譜線，并從實驗中求得各色譜線的折射率，定性分析折射率和波長的關系，直觀形象，但是未深入探究原子譜線的產生機理［1］.

實際上，學生對于譜線特征的理論分析，更多是以堿金屬原子譜線為案例.經典的《原子物理學》教材［2］，以鋰原子為例介紹四類線系，以鈉原子為例介紹量子缺，以鈉原子3P→3S譜線為例介紹譜線的精細結構分裂，等等.在近代物理實驗中，“鈉原子光譜實驗”是一個經典實驗.其關于原子性質認識的實驗設計具有重要的啟發作用和借鑒意義.學生利用較為精密的儀器，通過軟件接收并獲得鈉原子譜線的波長和能量數據，并以此計算鈉原子各能級的量子缺，繪制原子能級，深入認識原子特性.該實驗中，內插法的數據處理過程比較復雜，學生過去少有接觸，因而不夠熟悉，可以在普通物理實驗課程中先行訓練.

由上可知，分光計對于光譜的觀察具有直觀性，而鈉原子光譜的實驗設計有效培養了學生的理論分析和數據處理能力.有一些學者在實驗的拓展上作了研究，例如鄧莉拓展分光計實驗，將測量數據擬合以柯西公式驗證［3］；朱洪玉將汞燈替換為鈉燈，從理論上分析了目視可得的鈉原子光譜的譜線波長［4］；蘆立娟、沈建堯測量并給出了鈉原子譜線的線系歸屬［5］；藍發超、唐宇給出了一種用Matlab計算鈉原子量子缺的快速方法［6］.但是這些研究都沒有嘗試將兩個實驗的思路結合起來.如果在普通物理實驗中，能有一種實驗設計，既能直觀地觀察到原子譜線，又能對測量結果進行較為深入的分析，這對于學生理解知識、培養思維以及提高實驗技能，都是大有裨益的.

基于以上想法，我們提出一個基于分光計的拓展實驗，利用分光計觀察和測量鈉原子的光譜，并利用內插法計算其量子缺.該實驗用普通物理實驗的方法，通過計算，獲得了近代物理實驗相關物理量的數據，是實驗設計上的一次創新，同時激發起學生的學習興趣，提高其對于物理直觀和物理圖像的認識.

1 實驗原理和思路

1.1 實驗原理

1.1.1 譜線的產生和量子缺［2］

對于氫原子，由里德伯公式可得，氫原子譜線的波數:

其中n和n′為主量子數，該式表示氫原子外層電子由主量子數為n′的能級躍遷至n時，產生的光子的波數.RH為里德伯常量，其大小可由基本物理量算出.若用mA表示原子核質量，me表示電子質量，則

由于鈉原子譜線主要由最外層電子的躍遷產生，此時可以看作類氫離子，因而鈉原子譜線的波數為

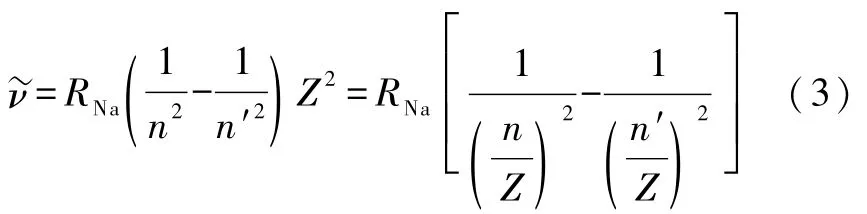
其中Z是有效核電荷數.相應地

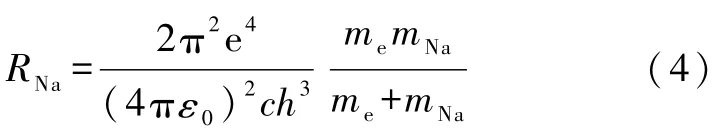
如果把波數計算公式的分母改寫，則可以記作

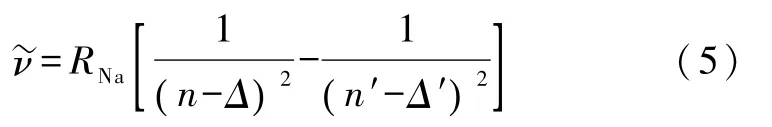
其中的Δ即為某一能級的量子缺.

考慮到每個主量子數 n都有 n個軌道角量子數，記作 l，其取值為 0、1、2、…、n-1，對應的光譜學標記分別為 S、P、D、….躍遷選擇定則要求躍遷前后Δl＝±1，因而對于鈉原子而言，會有 nP→3S（主線系），nS→3P（銳線系），nD→3P（漫線系），nF→3D（基線系）等4種線系.一般而言不同的軌道角動量對應不同的量子缺數值，因而相應地會有 Δs、Δp、Δd、Δf等量子缺值.

1.1.2 最小偏向角和折射率［7］

均勻介質對于一定頻率的光而言，有一定的折射率.當光通過三棱鏡時會發生折射，入射光線和出射光線有一夾角δ.δ有一最小值，稱為最小偏向角，記作 δmin.如圖1所示，設三棱鏡的頂角為 α，當入射和出射光線的夾角等于最小偏向角時，可以算出該頻率對應的折射率

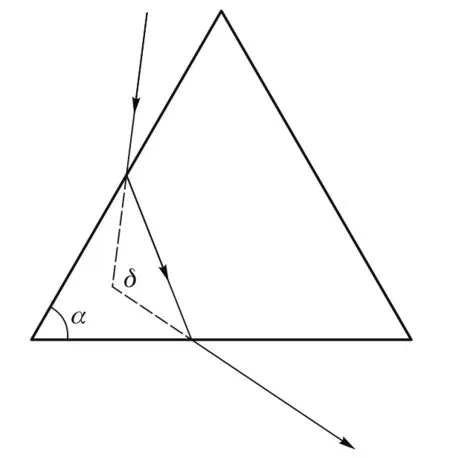
圖1 三棱鏡折射光路示意

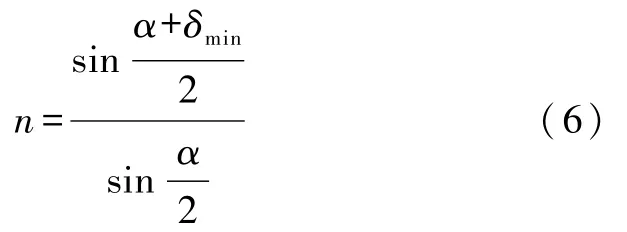
因而只要測量出頂角和最小偏向角，即可得到折射率.由柯西色散公式，保留到4次項，有

只要代入已知波長對應的折射率，即可求解得到待定系數.進而代入未知波長光譜的折射率，可以反推出光的波長.

1.2 實驗思路

本實驗的核心問題有二，即鈉原子光譜線的波長測量和基于波長的能級量子缺的計算.考慮到分光計無法直接測量波長，故可以利用柯西公式過渡.首先，利用分光計測量三棱鏡的頂角和汞燈黃、綠、紫譜線的最小偏向角，計算譜線的折射率；其次，通過數據擬合，得到保留4次項的柯西公式；最后，利用鈉燈測量出的最小偏向角計算折射率，代入公式反求其波長.這便完成了波長的測量.在波長測量的基礎上，通過內插法數據處理，可以得到鈉原子的能級量子缺.

2 實驗內容和數據

2.1 測量三棱鏡的頂角

利用“二分之一調節法”［8］調節好分光計后，利用自準直法［3］測量三棱鏡的頂角.旋轉望遠鏡，讀出其分別垂直于三棱鏡兩個面時的表盤示數，獲得數據如表1.

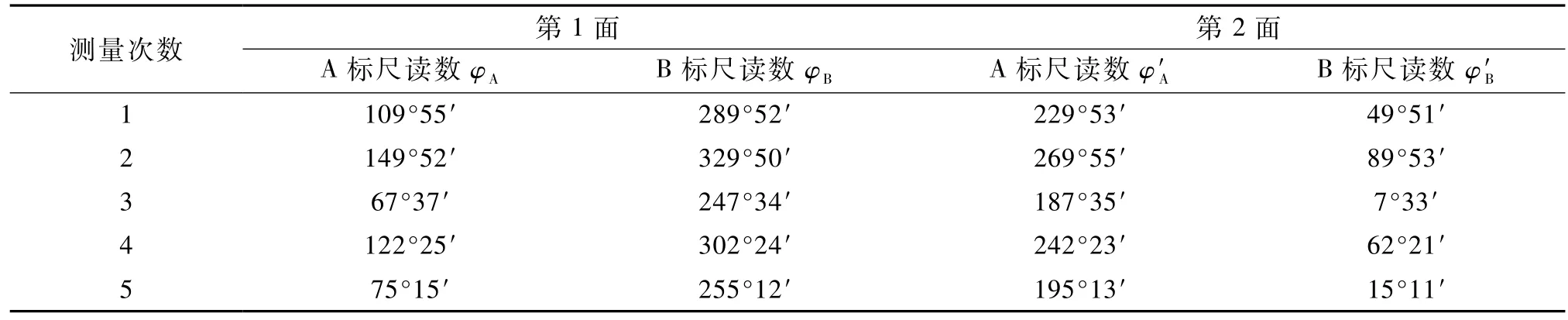
表1 三棱鏡兩個面位置的測量

三棱鏡的頂角

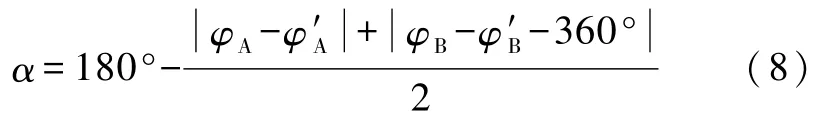
2.2 汞光譜折射率的測定

開啟汞燈，恰當地擺放三棱鏡的位置，使靠近望遠鏡的一面盡量與汞燈的光路垂直［3］.仔細調節望遠鏡的位置，直至觀察到視野中有色散譜線，其中有兩條黃色、一條綠色、一條紫色譜線，按從左向右的順序展開.各譜線強度視覺上相近.選定一條譜線后，轉動小平臺，使得視野中該譜線先向一側移動、又反向移動，反復幾次找到轉折點，轉折處對應的角度即為最小偏向角.測量數據在表2—表6中.

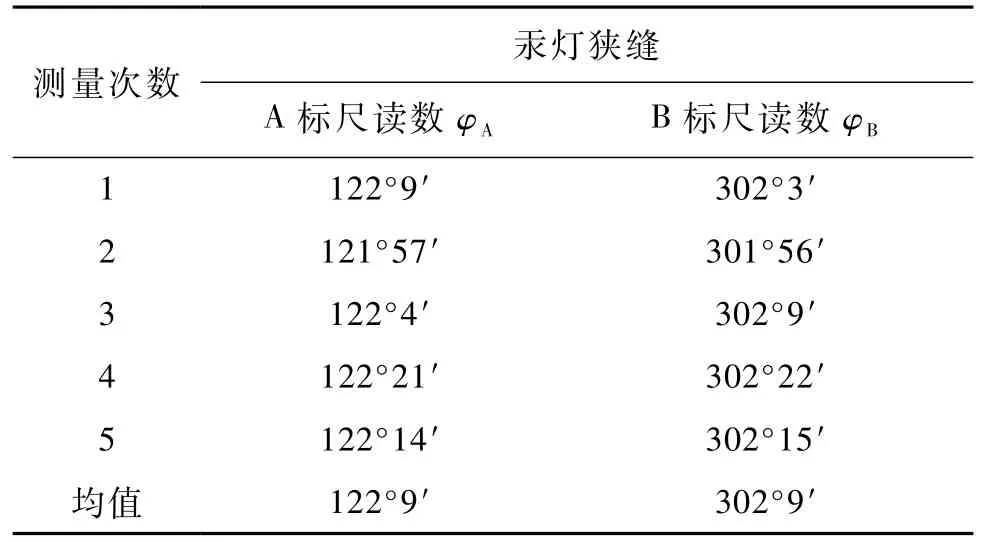
表2 汞燈狹縫位置的讀數

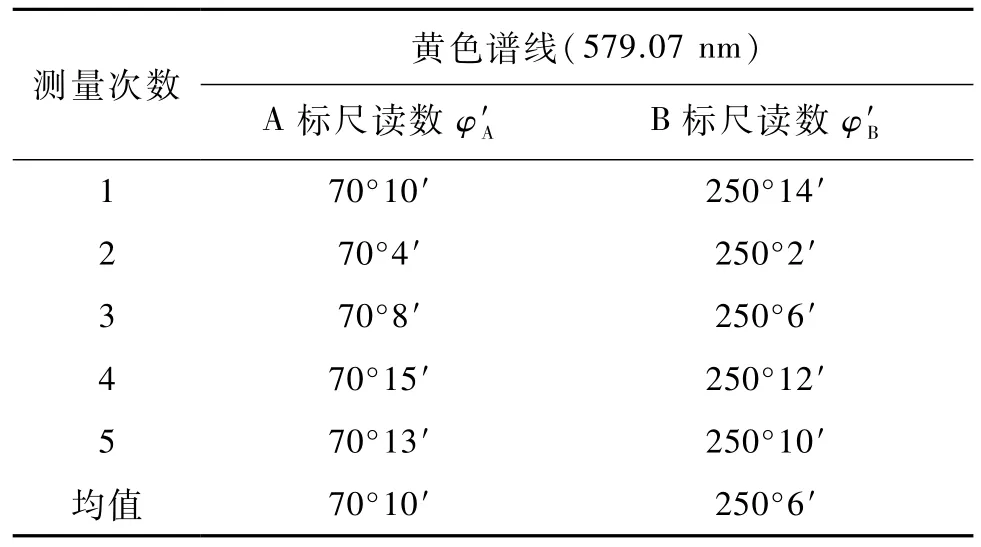
表3 黃色譜線（579.07 nm）位置的讀數

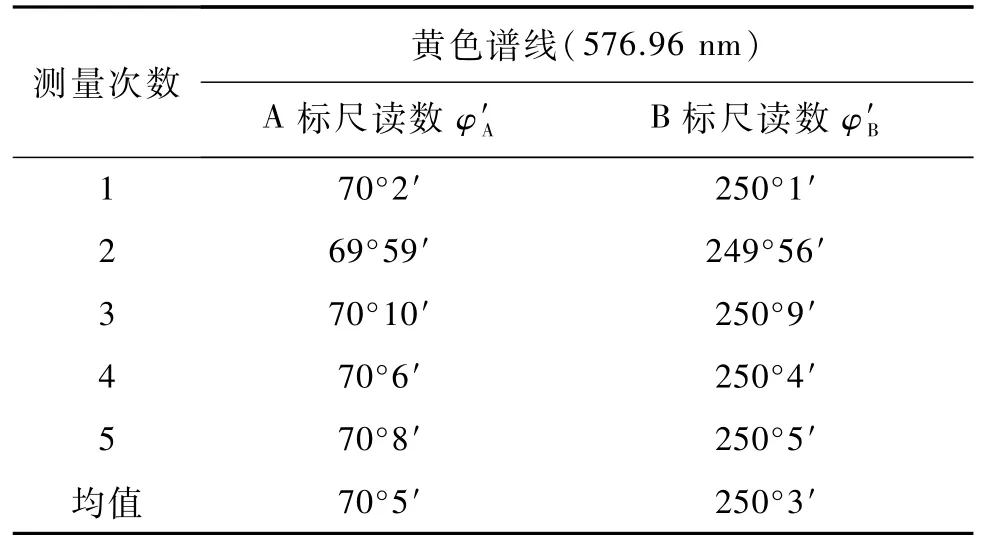
表4 黃色譜線（576.96 nm）位置的讀數

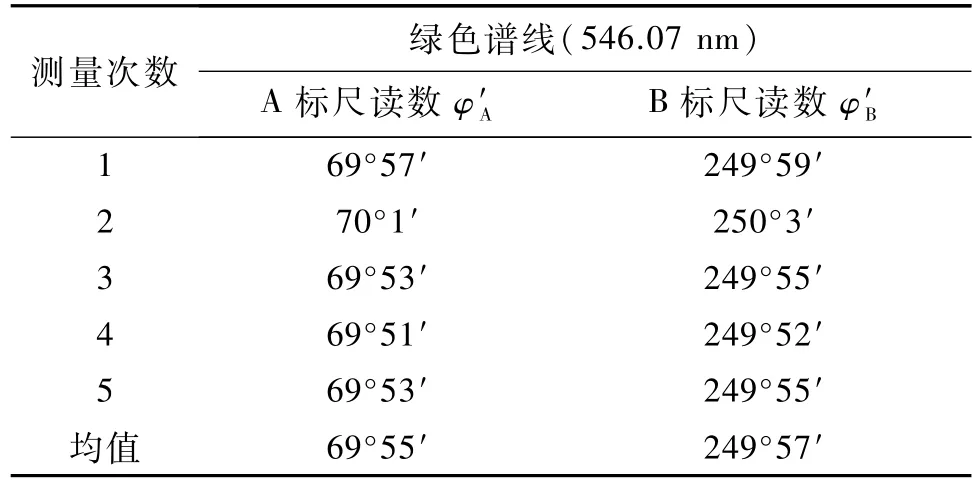
表5 綠色譜線（546.07 nm）位置的讀數

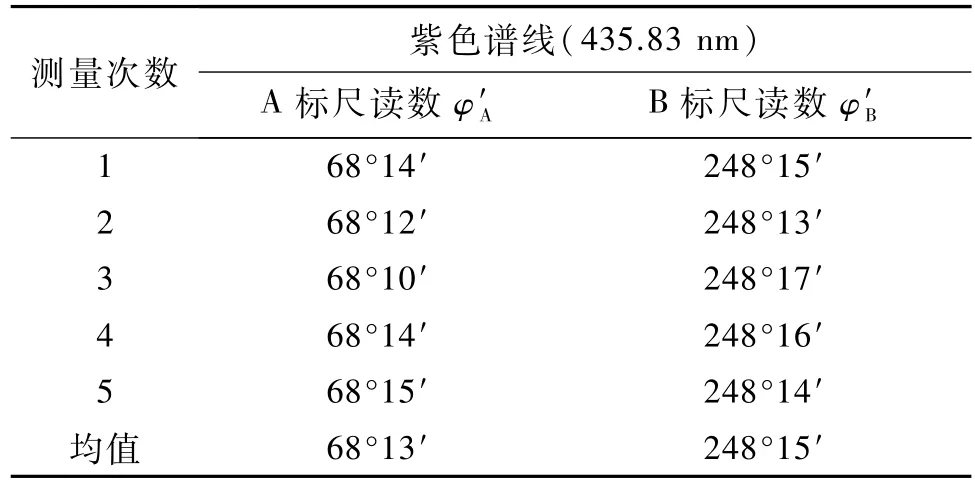
表6 紫色譜線（435.83 nm）位置的讀數

由

可以算出最小偏向角，進而算出折射率.利用平均值的計算結果，如表7所示.

表7 汞燈譜線波長和折射率的關系

依據柯西公式，擬合出結果如圖2所示.擬合式為

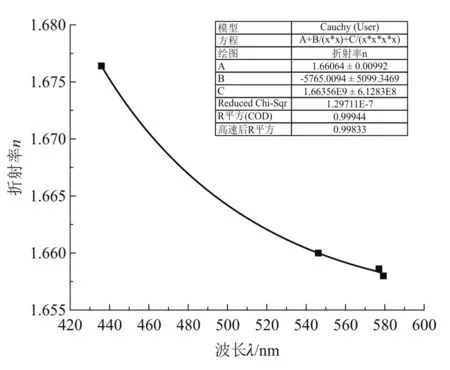
圖2 折射率-波長擬合示意圖

2.3 鈉光譜的測定

依照上述方法，將汞燈換為鈉燈，進行狹縫和譜線的測量.可以看見紅色、黃色、綠色三色的譜線.由于鈉燈中黃雙線強度較大，在視野中難以分辨，故取黃線的中部代替兩根黃色譜線分別測量.測量結果如表8—表11.

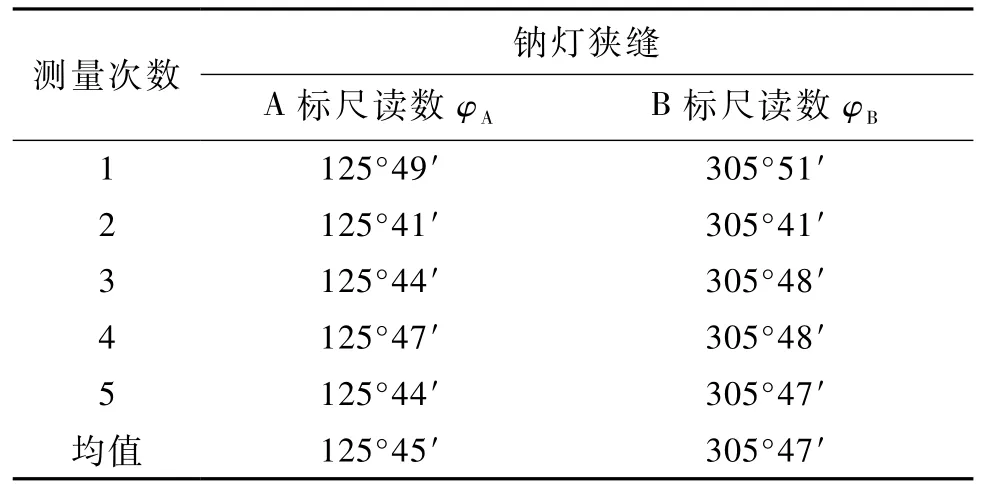
表8 鈉燈狹縫位置的讀數

表9 紅色譜線位置的讀數

表10 黃色譜線位置的讀數

表11 綠色譜線位置的讀數

類似地，可以算出最小偏向角，進而算出折射率.再將折射率代入柯西公式，即可解出對應的波長，結果見表12.

表12 鈉燈譜線折射率和波長的關系

將求算出的波長與理論分析得到的譜線值對照可知［5］，紅色為 5S→3P的譜線，屬于銳線系；黃色為3P→3S的譜線，屬于主線系；綠色為6S→3P的譜線，也屬于銳線系.

3 鈉原子量子缺的計算

3.1 鈉原子s能級的量子缺

考慮每一組線系中相鄰譜線的波數差

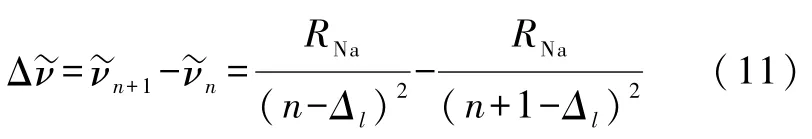
為計算方便起見，可以令

其中m為整數，a為正的小數.這樣

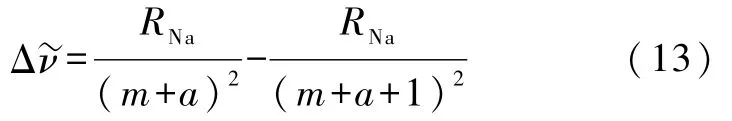
為了培養學生的數據處理能力，我們選用內插法，通過對里德伯表的查詢，獲得未知量m和a.內插法的基本思路如下:依據里德伯表的標準［9］，這里取RNa＝109 737.31 cm-1.求出的波數差 Δ介于表中波數差Δ和Δ之間，可以從表中讀出這兩個波數差對應的m值，記表中兩個波數差對應的a值分別為a1和a2，則由內插法可得實際的a值應當為

然后依據代換關系，可以計算出量子缺:

利用銳線系的兩條譜線即可算出s能級的量子缺.經過計算，可得Δν?＝3 158.10 cm-1.從表中可知，對應“34”，即 m＝3；其對應兩側 a1＝0.66，a2＝0.64，Δν?1＝3 138.66 cm-1，Δν?2＝3 185.27 cm-1，于是由公式可得 a＝0.652，因此 Δs＝n-（m+a）＝ 1.348.

3.2 鈉原子p能級的量子缺

由于沒有多組主線系的譜線數據，所以不能用上述方法計算p能級的量子缺.但是可以從線系限的角度考慮.考慮到銳線系固定項

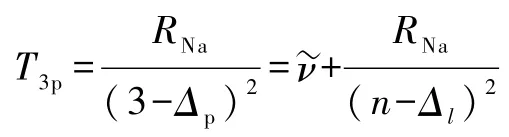
可以直接利用已知的光譜數據求算，將該數值代入里德伯表，按內插法可以求出p能級的量子缺.

4 分析討論

由擬合結果可知，對于參數 A的擬合較好，但是參數B的不確定度較大.由作圖可知，汞的黃雙線測量和擬合結果偏差較多，主要是兩根黃雙線較為接近、不易分辨，且目鏡存在視差，導致測量不夠精確.

依照測量出的最小偏向角反求鈉光的波長，并求算其量子缺的結果，與文獻［6］中的精確計算值符合得較好，說明該方法是可以正確得到鈉原子的譜線數據和量子缺的.由計算可知，s能級的量子缺比p能級要大，這可以用軌道貫穿和實極化解釋.如果考慮經典的電子軌道，隨著角量子數l的增大，軌道越接近正圓，也即越接近玻爾模型，有效電荷 Z較小，這樣量子缺就較小；相反，如果l較小，則軌道偏心率較大，可能會穿過原子實，此時受到原子實的吸引會比外側軌道更強，因而有效電荷 Z更多，這樣量子缺就更大.

當然，由于本實驗的觀察和測量手段限制，只能得到鈉原子光譜可見光區的有限三條譜線，對于量子缺的計算是比較粗略的.但該實驗進一步強化了學生對于分光計的使用，同時介紹并訓練了內插法的處理思路，為近代物理實驗中鈉原子光譜的精細實驗打下了基礎.

5 結束語

本實驗將普通物理和近代物理兩個經典的實驗相結合，從定性直觀的角度觀察汞原子和鈉原子光譜，從定量理性的角度導出折射率的公式、求出鈉原子譜線的波長，進而利用內插法計算鈉原子譜線的波長和量子缺.在整個過程中，既有實驗的操作，又有仔細的數據分析，達到了實驗創新訓練的目的.基于這樣的思路，還可設計其他結合拓展實驗，在普通物理實驗中有近代物理實驗的思維，讓近代物理的理論學習直接指向可見、可做的普通物理實驗.