定點運動轉軸唯一性與歐拉角位移矢量性討論

徐晨昊，張亞紅

（1.西安交通大學 機械學院，陜西 西安 710049；2.西安交通大學 航天學院，陜西 西安 710049）

剛體的定點運動可看成剛體繞一系列過定點的瞬時轉軸的連續轉動，關于定點運動的討論是理論力學研究中的重要問題［1，2］.理論力學教材中通常先采用幾何法證明達朗貝爾-歐拉定理，即定點運動剛體的任何有限位移可通過繞過定點的等效轉軸的一次轉動實現，再令運動時間趨于無窮小，定性地得到存在瞬時轉軸的結論.幾何證明法因不能確定等效轉軸和瞬時轉軸是否唯一而有失完整性.

目前已有文獻使用幾何法直接證明瞬時轉軸的存在性，用反證法證明其唯一性［3］，也有文獻利用解析法證明等效轉軸的存在性［4］，經典理論力學教材中也包含瞬時轉軸存在性的解析證明［5］.若能采用解析法進一步對等效轉軸和瞬時轉軸的唯一性進行論證，對于充實和完善剛體定點運動的描述將具有重要意義.

現行理論力學教材公認剛體定點運動的角速度矢量與瞬時轉軸共線，通過反證法說明有限歐拉角位移具有不可換序性，從而證明了有限歐拉角位移不是矢量，不能合成為繞等效轉軸旋轉的角位移.同時通過特例證明無限小歐拉角位移是矢量，角速度矢量與歐拉角變化率之間的關系為

ω ＝ ψ·+θ·+φ·（1）

若能夠對于式（1）進行嚴格的一般性證明，則可進一步完善剛體定點運動的描述，并對本部分教學工作具有很好的參考意義.

本文采用解析法，通過矩陣運算闡明等效轉軸與初末狀態的過渡矩陣之間的關系，進而對等效轉軸的唯一性進行證明，并嚴格證明有限歐拉角位移不是矢量的結論.之后證明瞬時轉軸的唯一性，并對無限小歐拉角位移是矢量的結論進行嚴格證明，同時基于該結論印證式（1）的正確性，并建立了瞬時轉軸的方位與歐拉角之間的關系.

1 等效轉軸與過渡矩陣的關系

設剛體做定點運動，定點為坐標原點O.［i j k］和［i′j′k′］分別為定坐標系和結體坐標系的單位方向向量，則

矩陣 A 為［i j k］到 [ i′ j′ k′]的過渡矩陣.同一個向量在這兩組基底下的坐標之間的關系為

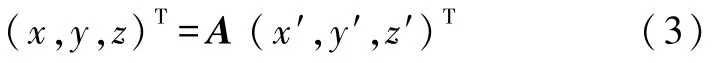
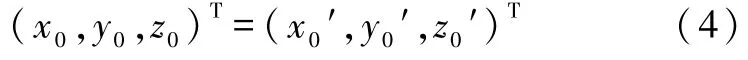
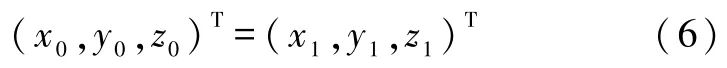
滿足式（6）的向量是等效轉軸的方向向量，該向量在定坐標系下的坐標向量記作e，由式（5）得

式（7）表明等效轉軸的方向向量為過渡矩陣A的特征值1所對應的特征向量.

2 矩陣法證明等效轉軸的唯一性

如式（2）所述，A是兩組三維標準正交基 Q＝［i j k］和 Q′＝ [ i′ j′ k′]之間的過渡矩陣，滿足

標準正交基構成的矩陣是正交矩陣.正交矩陣可逆，其逆矩陣和轉置矩陣也是正交矩陣，正交矩陣的乘積依然是正交矩陣.由以上性質可知A＝Q-1Q′也是正交矩陣.

剛體定點運動可用圖1所示歐拉角描述.設Q到Q′的歐拉角為ψ、θ、φ，則過渡矩陣A可表示為

圖1 歐拉角示意圖

其中

因為歐拉角與剛體定點運動的位置一一對應，所以任意一個有限位移的過渡矩陣是唯一的.經運算可知

正交矩陣的特征值具有以下性質:若特征值為實數，則其必為+1或-1；若特征值為復數，則其必成對出現，且互為模等于1的共軛復數.A為三階正交矩陣，在復數域內有三個特征值λ1、λ2、λ3，且三個特征值滿足

結合式（14）和正交矩陣特征值的性質分析可知，矩陣A只可能有一對復特征值或不含復特征值.當矩陣A有一對復特征值時，剩下的一個特征值必為1；當矩陣A沒有復特征值時，因為A不是單位矩陣，所以三個特征值只能為λ1＝1，λ2＝ -1，λ3＝-1.由此可知，過渡矩陣 A一定有單特征值1，所以式（7）中的特征向量e存在，即等效轉軸存在.

特征值 1的代數重數是指代數方程det（A-λI）＝0的根 λ＝1的重數，由上文可知其為1.特征值1的幾何重數是指特征方程（7）的基礎解系所含有的向量個數.根據線性代數理論可知，矩陣A的任何特征值的幾何重數不大于其代數重數，又因為幾何重數至少為1，所以幾何重數只能等于1，即A的特征值1對應的特征向量只在一維向量空間中分布，因此等效轉軸是唯一的.

至此，剛體定點運動有限位移的等效轉軸的唯一性證明完畢.

3 有限歐拉角位移的矢量性討論

剛體定點運動有限位移可以分解為進動、章動和自轉.假設歐拉角位移具有矢量性，根據位移的等效性，三個歐拉角位移合成結果應當等于剛體繞等效轉軸旋轉的角位移.

如圖1所示，進動、章動、自轉的角位移分別沿z軸、節線 ON、z′軸.z軸、節線 ON、z′軸的方向向量以k、n、k′表示，則歐拉角位移在定坐標系下的表示形式為

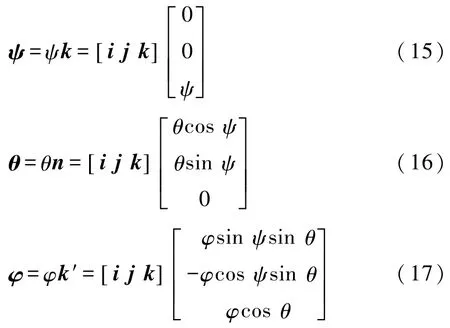
設向量 b＝ψ+θ+φ，則

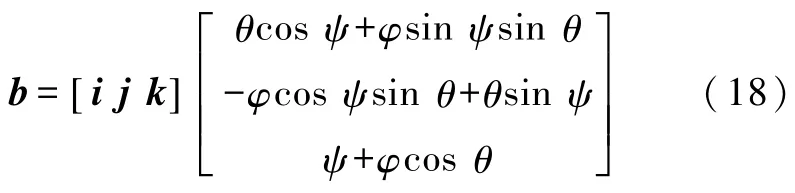
根據式（9）—（12），利用 MATLAB 計算可知

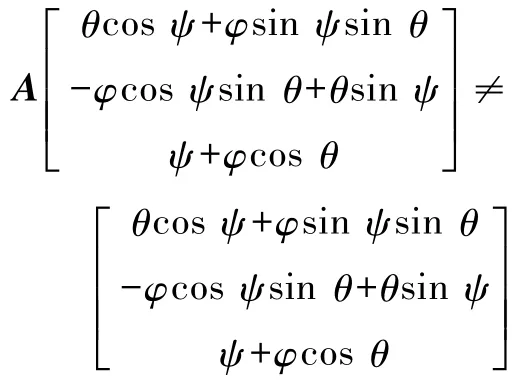
由此可見向量b不滿足式（7），所以其不是該有限位移的等效轉軸的方向向量.該結論與位移的等效性相違背，所以假設本身即是錯誤的.

綜上可知，歐拉角位移不是矢量.

4 矩陣法證明瞬時轉軸的唯一性

在無限小的時間間隔Δt內截取上述有限位移中的任意一段無限小位移，并且其初末狀態的結體坐標系不重合.設結體坐標系在無限小位移前后的標準正交基 [ i1j1k1]和 [ i2j2k2]對應于定坐標系[i j k]的過渡矩陣分別為 B和 C，且 B＝B1B2B3，C＝C1C2C3，其中

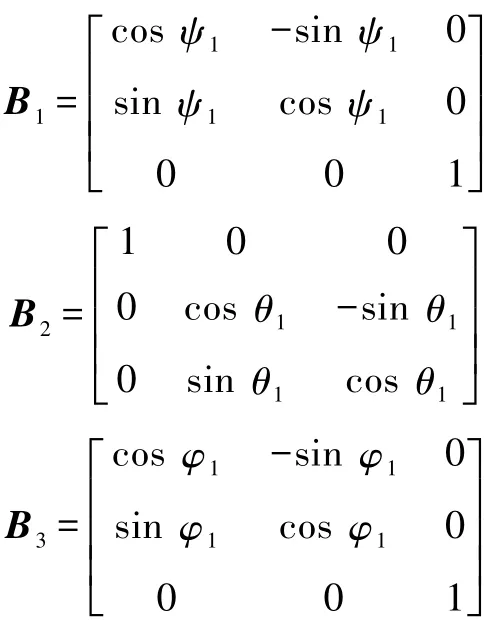
B和C滿足

根據式（19）和式（20），設 [ i1j1k1]到 [ i2j2k2]的過渡矩陣為D，則

因為B和C皆為行列式為1的正交矩陣，所以D 也是正交矩陣，且 det（D）＝ det（BT）det（C）＝ 1.因此，依照與第2部分完全相同的證明方式可知，該無窮小位移的等效轉軸是唯一的.由于 Δt→0，所以該等效轉軸即為瞬時轉軸.又因為該無窮小位移是任意選取的，所以剛體定點運動任意時刻的瞬時轉軸具有唯一性.

5 無限小歐拉角位移的矢量性討論

由上文可知剛體位移趨于零時滿足

因為矩陣B的所有元素均可視作為關于ψ、θ、φ的一階連續可導函數，所以B存在全微分

矩陣C和矩陣B無限接近，因此矩陣C可表示為

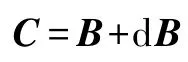
將式（22）代入上式可得

據上文所述，矩陣D＝BTC代表無限小位移的過渡矩陣，將式（23）代入矩陣 D并利用 MATLAB軟件進行計算，得到過渡矩陣D的表達式，它是一個單位矩陣I與一個無窮小量矩陣 H的和.矩陣D的第一行元素為

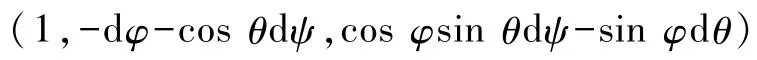
第二行元素為

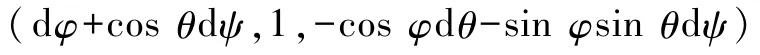
第三行元素為

求解矩陣D的特征值1對應的特征（坐標）向量，從而得到瞬時轉軸的方向向量.

設r為坐標原點到剛體上某一點的向量，則

dr是其經過該無限小位移后的變化量

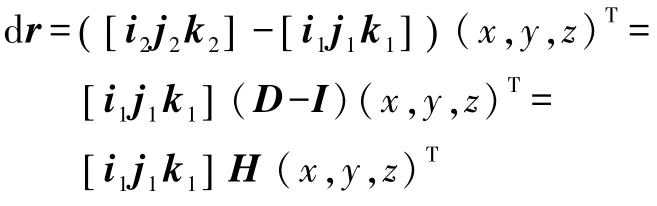
經MATLAB軟件計算可得

由此可知dβ是該無限小位移所等效的旋轉角位移.

將式（24）展開可得

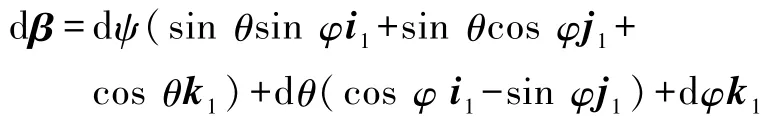
對比式（15）—（17）中的表達式，并假設無限小歐拉角位移是矢量，可得

由式（26）可知，無限小歐拉角位移的矢量和等于繞瞬時轉軸的等效旋轉角位移，滿足位移的等效性，因此假設成立.綜上所述，無限小歐拉角位移是矢量.

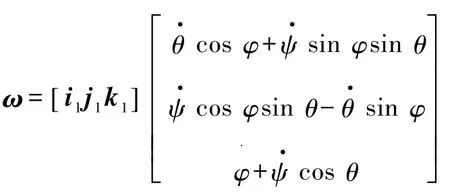
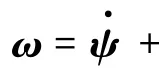
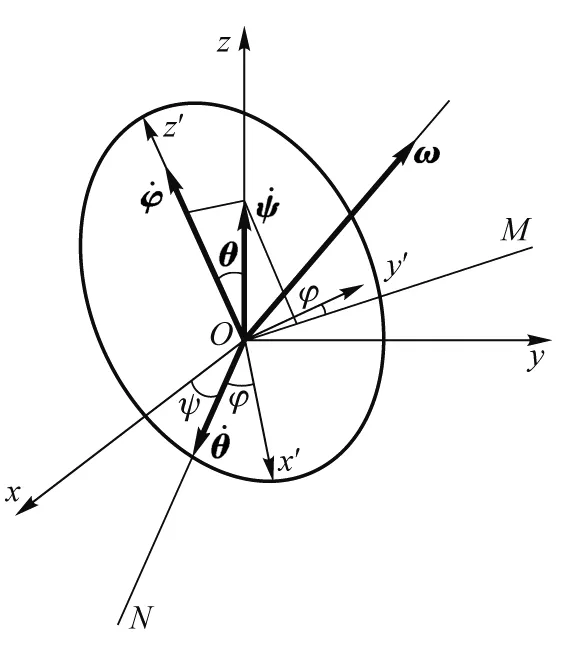
圖2 剛體定點運動角速度示意圖

6 結論

1）證明了剛體定點運動等效轉軸的唯一性，并給出了等效轉軸應滿足的條件:方向向量為過渡矩陣A的特征值1對應的特征向量.

2）通過矩陣運算，論述了有限歐拉角位移不滿足矢量運算的性質，從而說明有限歐拉角位移不是矢量.

3）在等效轉軸唯一性的證明基礎上，進一步利用矩陣及其特征值的性質，證明了剛體定點運動瞬時轉軸的存在性和唯一性.

4）從角位移和角速度的定義出發，借助矩陣全微分運算，證明了無限小歐拉角位移是矢量，并建立了瞬時轉軸方向向量與歐拉角之間的關系.

應當指出，上述證明和分析除了對剛體定點運動的相關結論給予嚴格的解析證明，分析過程也展示了矩陣及其特征值性質在復雜剛體運動分析中的優勢.