兩狹長平行板間液橋兩端體積的計算
陽 麗,程震宇,蕭華鵬
(廣西師范大學 物理與科學技術學院,廣西 桂林 541004)
當兩固體之間的接觸部分或者間隙部分存在微量液體時,在兩物體表面間會出現液橋現象[1].對液橋的研究可為顆粒/粉體團聚、毛細黏附力、微/納系統、多孔材料的某些特性研究提供幫助[2].研究液橋的體積也是微重力流體力學、毛細力學中的一個課題[3].
大部分文獻關注兩球形體之間的液橋,對于平板間液橋體積的計算相關文獻較少[4-7],例如,Broesch[4]利用 Surface Solver軟件模擬狹長裂縫幾何形狀中非軸對稱毛細管橋的形態演變.莊大偉[5,6]等人考慮液橋重力和表面張力作用下液橋的接觸角隨著方位角的變化,對液橋三相接觸線采用橢圓方程描述,計算了兩豎直翅片間液橋體積.朱朝飛[7]通過張力等效方法建立液橋的三維受力模型,采用不考慮重力的球形近似求解液橋形態微分方程,得到狹長平行板間液橋的形態特征參數與液橋受力之間的關系.實際上,兩平板間液橋并不為規則的柱體[8,9],而是兩端呈現類似馬鞍形狀.在以往的文獻中都采用軟件模擬或者近似為柱體的方法對液橋的體積進行計算,未有過在理論上對狹長平板間的液橋體積進行精確計算.
本文考慮液橋兩端的實際形狀,以狹長的兩平行板間的液橋作為研究對象,建立忽略重力的三維液橋模型,計算液橋的兩端(類馬鞍形)的體積.在計算過程中將多個液橋的形態特征參數用扎釘角表示出來,得到體積與高度和扎釘角的關系,從而得到體積的清晰數學表達式.
1 液橋的模型
圖1中兩平行板之間的陰影部分表示液橋,側面和端面為液體和氣體的交界面,根據毛細力學的相關知識,隨著固液界面的收縮,在表面張力的作用下,忽略重力影響,穩定后的氣液徑向界面的形狀將會趨近于圓弧形[10].液橋為兩端近似馬鞍形、中間凹陷的長條狀的全對稱形狀.圖中液橋的相關形態表征參數有多個.θ表示接觸角,α表示扎釘角,H表示兩板之間的高度,W表示板子之間的寬度.Rn表示液橋兩端馬鞍形液體中間最細處的半寬度,rc為兩側的氣-液交界面曲率半徑,rd為兩端的氣-液交界面曲率半徑.
2 液橋兩端的體積計算
由于液橋兩端的馬鞍形狀[圖1(e)]具有對稱性,因此把左右兩端合并計算.采用高等數學中計算旋轉體體積的柱體方法[11].我們沿著 xy平面將高度區間(z方向)內分割成無數個高度為 dz的 “薄片”,近似地把這些“薄片”看作一個個底面為橢圓的柱體.每個柱體的體積為 πxmymdz.其中 xm和 ym,分別對應橢圓的長半軸、短半軸的長.液橋兩端角度的積分微元為 β1,兩側角度的積分微元為 β2,范圍分別為,β1為 0~(π-2θ),β2為 0~(π-2α).由圖 1得出
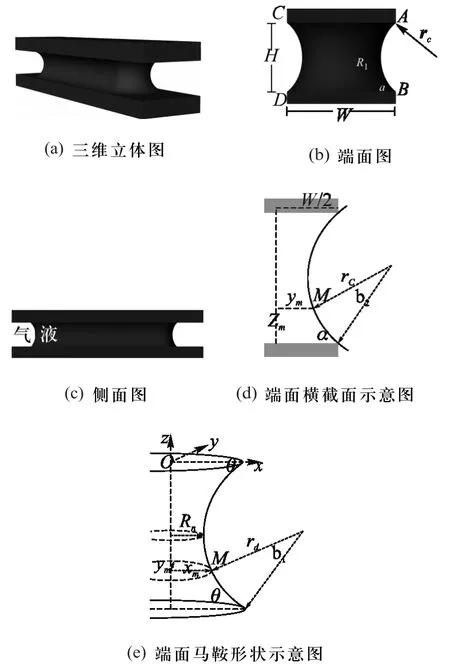
圖1 兩平行板間的液橋模型
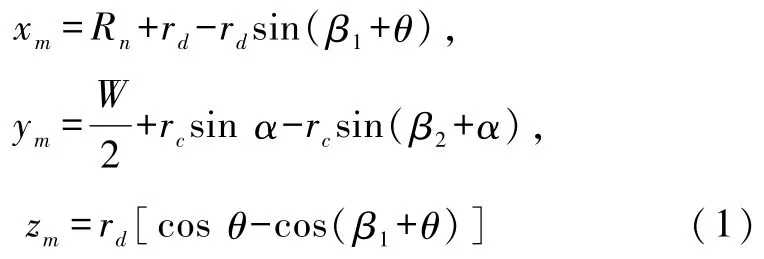
無論兩側面還是兩端面z方向高度應相同,得到 β1和 β2的關系為
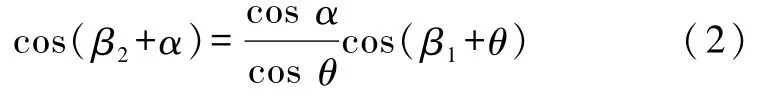
液橋兩端馬鞍形的總體積為
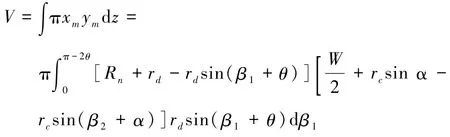
由于公式較長,為了方便計算,將與積分微元無關的項用A、B表示:
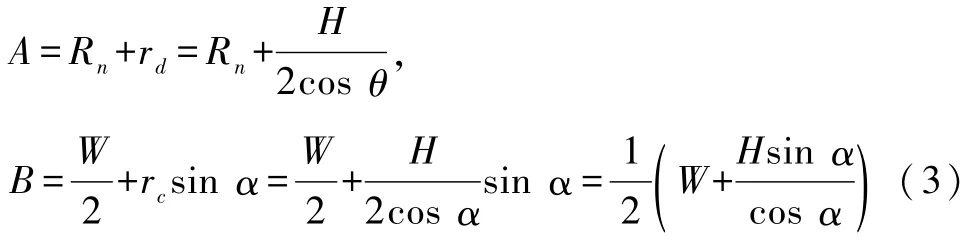
于是
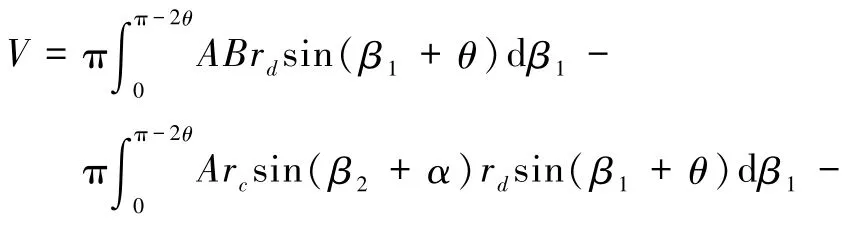
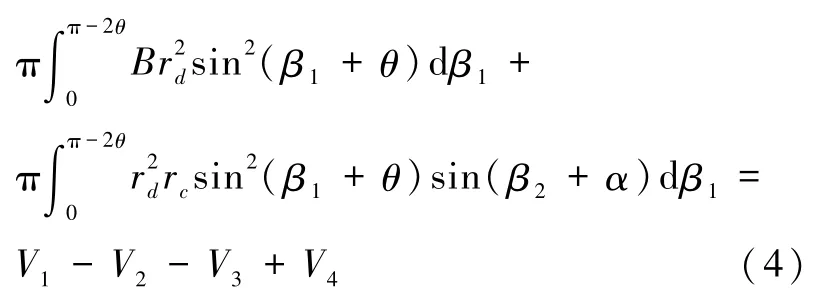
可計算得到
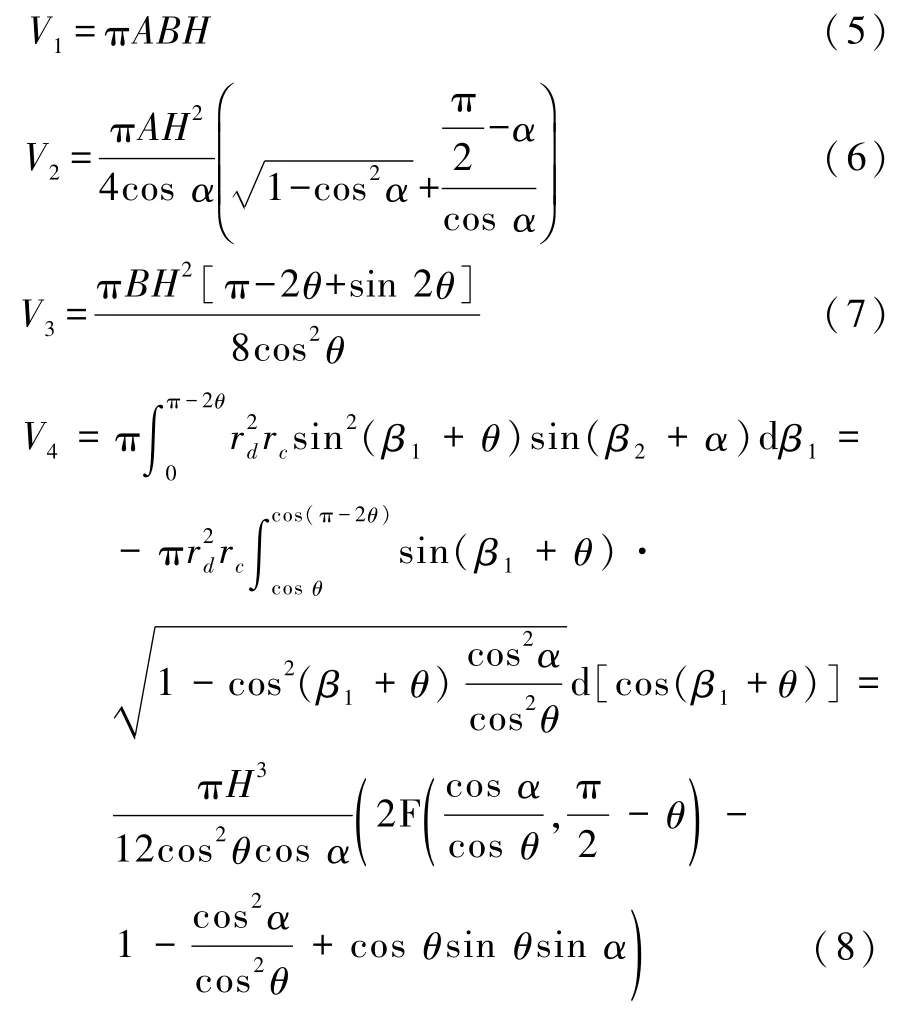
其中 F表示第一類橢圓積分[12]:
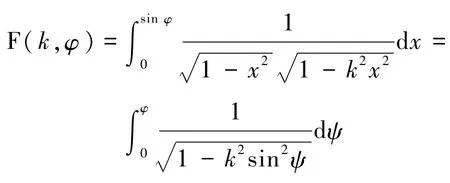
第一類橢圓積分級數表達為
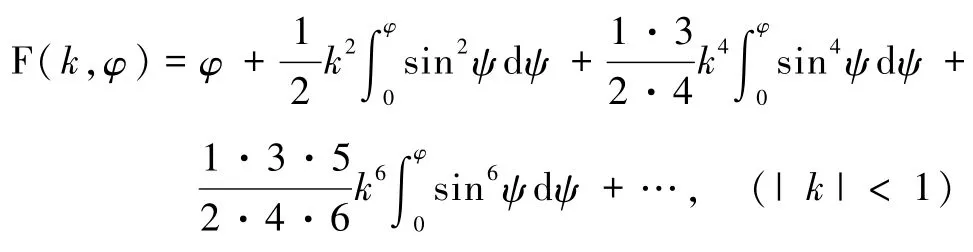
所以液橋兩端馬鞍形總的體積有
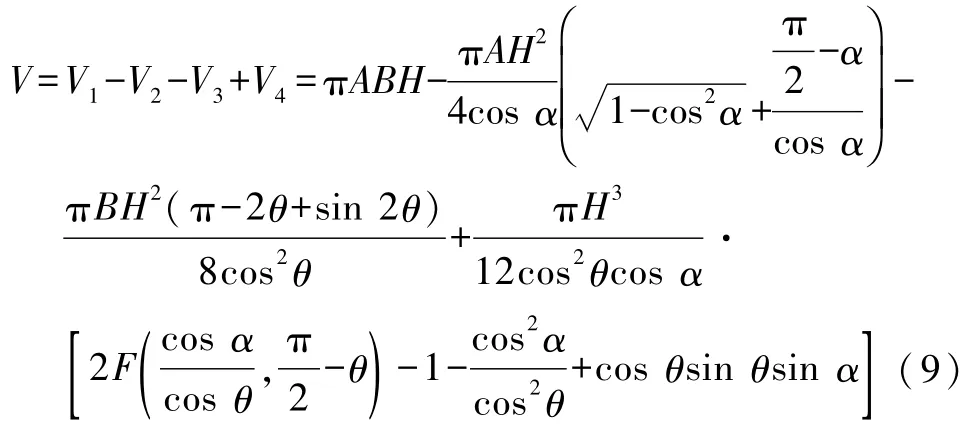
其中,根據圖1中的幾何關系可以得到
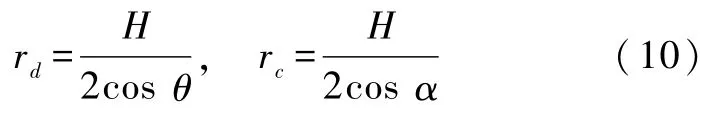
根據流體靜力學的Pascal定律,液橋兩端和兩側的內外壓強差相同,根據Young-Laplace方程,可得
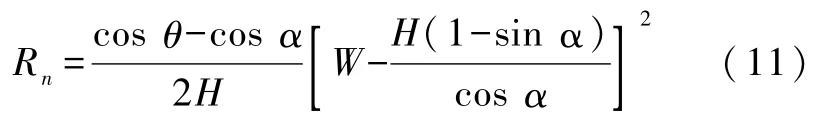
于是,體積函數可以簡寫為 V=V(H,W,θ,α,rd,rc,Rn),當體積 V、W、θ、H 為可測量的已知量的時候,通過式(10)、(11)可以得到 V 與 H、α 的關系式,進而得到扎釘角 α隨著H變化的數值結果.總之可以根據測量得到的液橋兩端體積 V,根據式(1)—式(11)得到α和Rn隨著 H變化關系的結果(圖2所示).從而可以得到液橋的各個形態特征參數,分析液橋的側面輪廓的形貌.
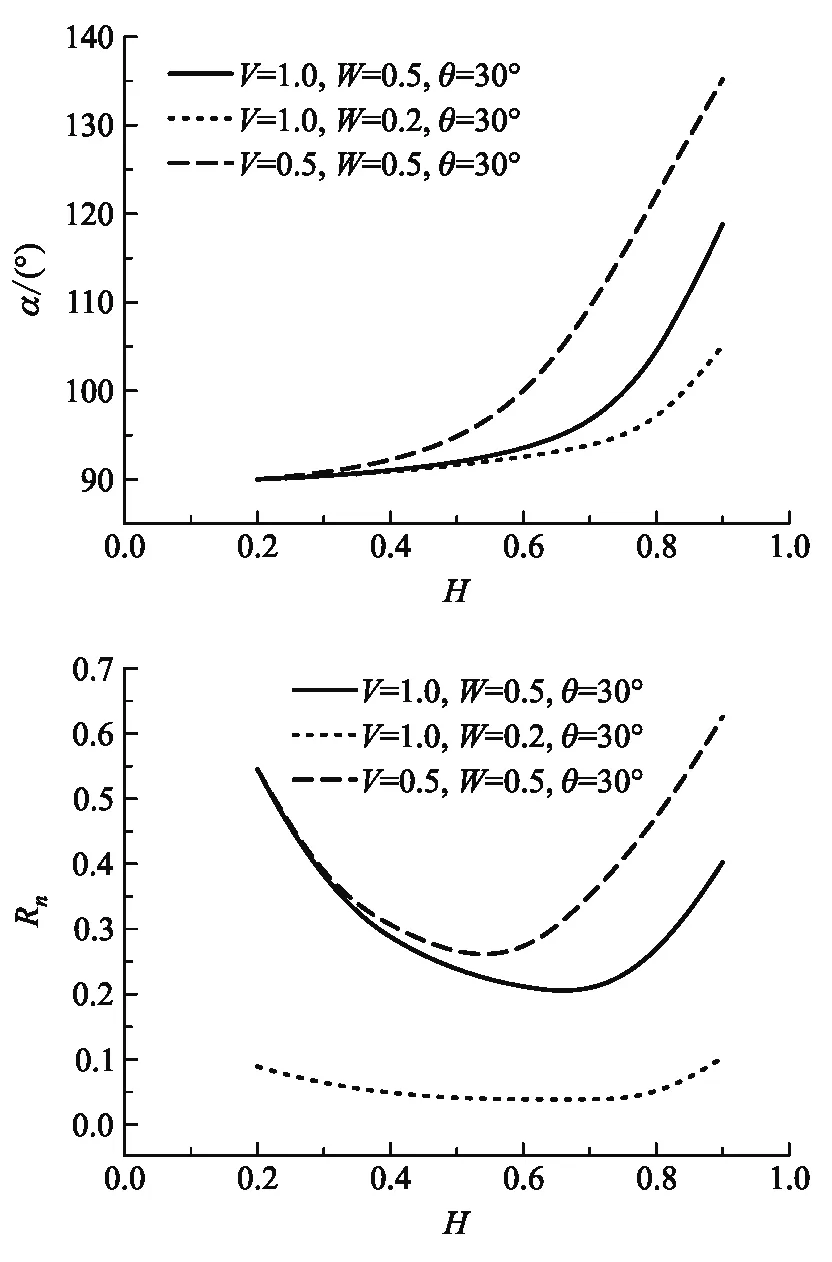
圖2 α和Rn隨著H變化的關系
從圖2中可以看出,V、W、θ對液橋的形貌起決定作用.板子寬度越寬,α角越大,液橋體積越大,液橋越長,α角反而越小,而液橋兩端的馬鞍形的突起部分Rn的數值是先減小后增大.隨著兩個平板之間距離的增大,扎釘角變化的規律與直覺是相反的,人們普遍認為兩板子越拉越開,液橋兩側和兩端都會變細.實際的計算結果表明,液橋兩側變胖,兩端回縮.在低高度處,釘扎角度通常小于90°,并且隨著高度的增加,釘扎角度可能會高達140°,即兩側面處的α角緩慢增大,如圖3所示.這與實驗觀察到液橋慢慢回縮“變胖”,變圓變短的情況是一致的,如圖4所示.這種變化意味著當兩表面距離增大時,液橋側面輪廓的曲率會從凹變為凸,馬鞍形狀的突起程度也相應變化.這是因為液橋的穩定形貌是由最小表面能決定的.由于表面張力的作用,使液體三相接觸線具有收縮趨勢,使液體表面積趨于最小,液面的穩定狀態遵循最小能量原理.關于液橋能量的詳細計算還有待深入的分析.
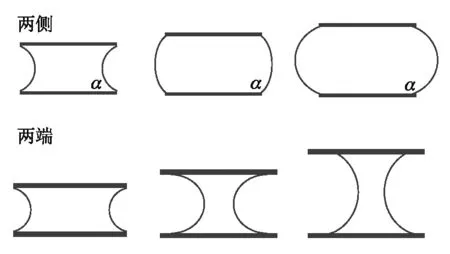
圖3 液橋的側面和端面的輪廓線變化示意圖

圖4 液橋隨著距離增大的圖像(液橋體積 1.0微升)
對兩板間的液橋進行物理模型的構建是一個復雜的思維過程,對于學生的學習來說,具有一定的科學性,分別為模型建立、模型計算分析和模型的實驗驗證3個步驟,通過3個階段的探索,教師開展科學建模教學,幫助學生掌握基礎知識和概念.
3 結論
本文考慮狹長的兩平行板間液橋兩端的真實形狀,建立三維液橋模型,推導出液橋的兩端(類馬鞍形)的體積,可計算得到液橋側面曲率半徑和扎釘角隨著體積和高度的變化關系.該計算方法基于旋轉體體積計算方法,液橋的形態特征參數用扎釘角、板間高度、寬度等重要參數表示出來,即可以加深學生對高等數學中的積分知識的理解,還可以培養學生建立物理模型的能力.

