例析數學實驗在初中數學教學中的應用

沈忠良

摘要：數學實驗教學注重讓學生在實踐的過程中體驗、學會和運用數學知識和方法，從而提升學生的數學核心素養。基于此，教師可以把數學實驗引入到課堂教學環節中來，從而激發學生主動參與學習的過程，促進學生在實驗中學會合作交流，進一步幫助學生理解數學的本質意義。

關鍵詞：數學實驗;學習興趣;合作學習;核心素養

數學實驗為學生提供了從事數學活動的機會，真正讓學生親歷數學發明創造的過程，幫助學生在自主探索和合作交流中掌握數學基礎知識，訓練數學基本技能，領悟數學基本思想，積累數學基本活動經驗。在初中數學課堂教學中引入數學實驗，為學生學習數學提供一些感性材料，是引導學生發現問題、提出假設，驗證猜想和解決問題的有效途徑，也是完善學生認知結構，提高學生數學核心素養的一個重要途徑。

一、數學實驗可以激發學生興趣，讓學生主動參與學習過程

數學實驗教學中，學生可以通過觀察、操作等實踐活動來進行數學學習，在這樣的學習過程中，學生不是被動接受現成的結論，而是從自己的“數學現實”出發，通過動手、動腦，用觀察、模仿、實驗、猜想等手段獲得經驗，逐步建構并發展為自己的數學認知結構。在數學實驗中，學生由于親自動手操作，所以更容易對實驗結果、產生結果的原因、新的知識以及新的方法等產生強烈的好奇心，因而能激發學生學習的興趣，調動學生的積極性。

[案例1]

在初一數學“一元一次不等式組”的概念教學中，教師可以使用天平這一實驗器材。先讓兩位學生根據要求依次上臺動手操作，然后提出問題：怎樣用天平來估計一支筆的質量？

實驗1：把一支筆放在已經調整至平衡狀態的天平的左側托盤內，在右側托盤內放置10g的砝碼，發現天平指針向左側傾斜，那么怎樣來表示筆的質量與砝碼的質量之間的關系呢？（由學生得到不等式：x>10）

實驗2：在右側托盤內放置20g的砝碼，發現天平指針向右側傾斜，那么怎樣來表示筆的質量與砝碼的質量之間的關系呢？（由學生得到不等式：x<20）

接著由學生總結得出：這支筆的質量大于10g并且小于20g，把兩個不等式用大括號連接起來，就可以寫出一元一次不等式組 。

教學思考：設計上述新課導入的方法，既使學生參與了實驗過程，又使不等式組的概念顯得更加直觀形象，幫助了學習困難的學生積極參與學習過程，提升了學生的學習興趣。后面教師只要再編擬幾個練習題，強化學生對概念的理解，那么就能促使學生由感性認識上升到理性認識。

二、數學實驗促進學生手腦并用，讓學生在活動中學會合作

數學實驗的實質是一種數學活動，是學生根據已有的數學知識和經驗，在老師指導下或與他人合作，并借助于一定的工具，對數學結論進行探索、驗證的過程。在數學實驗中，學生相互合作、相互依賴，形成了良性的合作互動的學習模式，學生的合作交流得到了很好的體現。通過數學實驗不僅能激發學生的創新思維，還能培養學生與他人合作的習慣。

[案例2]

在初一數學“感受概率”的教學中，教師可以組織學生進行擲硬幣的實驗。

步驟1：創設情境，合理猜測

任意擲一枚均勻的硬幣，若正面朝上，那么甲獲勝，若反面朝上，則乙獲勝。想一想：這個擲硬幣的游戲公平嗎？

步驟2：開展實驗，收集數據

首先，兩人之間輪流擲20次硬幣，記錄數據并計算正面朝上的頻率。其次，用表格的形式匯總各組的數據，分別計算試驗20次、40次、80次……400次時正面朝上的頻率。最后，將所得數據繪制成折線統計圖。

步驟3：驗證猜想，形成概念

從下表中的數據可以發現，在大量的重復實驗中，任意擲一枚均勻的硬幣，正面朝上的可能性趨向于0.5。

由此發現規律：若正面朝上的可能性大小用P來表示，則P= ，即硬幣正面朝上的概率為 。

教學思考：在數學實驗中，學生通過自主探索、合作交流的學習方式，形成概念。學生由一個旁觀者轉變成一個活動參與者，有利于激發學生的學習興趣，培養學生的創新思維與合作精神，幫助學生積累搜集、處理數據的經驗。

三、數學實驗使抽象數學形象化，讓學生理解數學的本質意義

信息技術的運用不僅為抽象的數學思維提供了直觀模型，而且為學生自主探索和構建數學模型提供了強有力的學習平臺。在數學課堂教學中，常常會碰到學生解題時因為找不到突破口而倍感困惑，此時教師可以引導學生利用“幾何畫板”軟件進行數學實驗，將蘊藏在數量關系背后的幾何意義直觀地展現出來，幫助學生理解數學的本質，提高學習效率。

[案例3]

有一張三角形紙片ABC，其中BC=6，∠C=90°，∠A=30°。

（1）如圖1，若用這張紙片裁剪出一個矩形CDEF，使點D、E、F分別落在AC、AB、BC上，且使矩形CDEF的面積最大，則點E應選在何處？

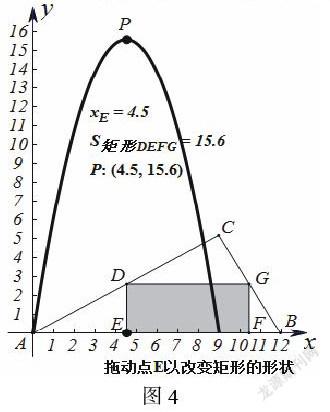
（2）如圖2，若用這張紙片裁剪出一個矩形DEFG，使點D、G分別落在AC、BC上，點E、F均在AB上，且使矩形DEFG的面積最大，則點E應選在何處？

對于上述題組，建立恰當的數學模型是解解決該問題的關鍵。“幾何畫板”為學生尋求解題模型提供了便利，能幫助學生有效突破難點。第（1）問中，若假設AE的長為x，則矩形CDEF的面積y可表示為y= ，用“幾何畫板”構造動點P（x，y），再運用動點追蹤功能，就能直觀地演示當點E在線段AB上運動時，動點P的運動軌跡（如圖3），幫助學生快速建立二次函數模型來解題。第（2）問中，也可以設AE的長為x，則矩形CDEF的面積y可表示為y= ，類似地用“幾何畫板”直觀地演示動點P（x，y）的運動軌跡（如圖4）。用“幾何畫板”將數、形之間的關系動態地展示出來，活躍了學生的思維活動，使抽象的數學知識變得生動形象，并且容易接受。

教學思考：在計算機信息技術環境中，學生自主探索知識的天地更為廣闊，學生參與學習活動的程度更高，因而“研究性學習”教學思想體現得更加充分。在上述案例中，學生參與實驗的過程也是一個數學思考的過程，學生也可以發揮自己的創造性，提出自己獨特的實驗設想，并與全班同學進行分享。

數學實驗是現代數學發展的必然產物，也是學生學習、理解和掌握數學的重要途徑。我們必須進一步加強數學實驗的研究與實踐，努力創設適合學生動手“做”數學的良好環境，幫助學生架起思維與建構之間的橋梁，充分發揮數學實驗在數學學習與能力發展等方面的積極作用，從而實現新課程標準提出的三維目標的融合，滋養學生的數學核心素養。

參考文獻

[1]袁麗華.數學實驗在初中數學教學中的應用分析[J].數理化學習（教研版），2020（03）：37-38.