n階多時滯微分方程的周期解

李文金, 龐彥尼

(1. 吉林財經大學 應用數學學院, 長春 130117; 2. 吉林大學 數學學院, 長春 130012)

0 引 言

時滯微分方程在生物數學、工程、經濟、信息等領域應用廣泛, 可用于描述動物血紅細胞再生、種群生態系統、心臟起搏等現象. 目前, 關于微分方程振動理論及其應用的研究已有很多成果[1-7], 特別是關于二階微分方程的研究已有較大進展, 但對于微分方程中含有多時滯量, 用上下解的單調迭代技巧處理其周期解的存在性和唯一性的研究文獻報道較少.

考慮n階時滯微分方程

-u(n)(t)=f(t,u(t),u(t-τ1),u(t-τ2),…,u(t-τn)),t∈

(1)

ω-周期解的存在性, 即滿足方程(1)和u(t+ω)=u(t)的解, 其中f:×n+1→連續且關于t以ω為周期,τ1,τ2,…,τn為正常數. 本文利用單位算子擾動理論, 通過建立新的極大值原理, 討論方程(1)ω-周期解的存在性和唯一性. 本文結果推廣了文獻[1]中二階多時滯微分方程

-u(2)(t)=f(t,u(t),u(t-τ1),u(t-τ2),…,u(t-τn)),t∈

ω-周期解的存在性.

1 預備知識

記Cω()是以ω為周期的全體連續函數按范數構成的Banach空間. 對()是以ω為周期的m階連續可微函數全體按范數構成的Banach空間. 記()是Cω()中的非負函數錐. 設Mn為正常數, 且

根據文獻[8]中引理2.4知, 微分算子Lnu=u(n)+Mu在周期邊界條件下滿足極大值原理, 且有下列引理.

引理1[8]設M∈(0,Mn)為一個常數, 則n階線性邊值問題

存在唯一解Φ∈Cn[0,ω], 且對?t∈[0,ω],Φ(t)>0.

引理2[9]設M∈(0,Mn), 則對?h∈Cω(),n階線性微分方程

-u(n)(t)+Mu(t)=h(t),t∈

(2)

存在唯一ω-周期解

(3)

且解算子S:Cω()()是線性全連續算子.

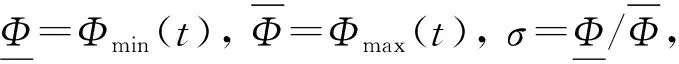
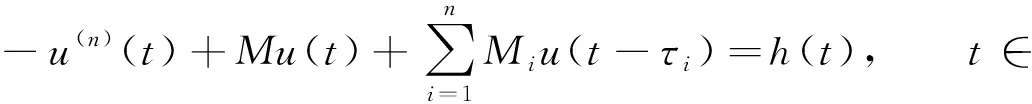
(4)

周期解的存在性, 其中M>0,Mi≥0.

引理3線性方程(2)的ω-周期解算子S:Cω()→Cω()具有下列性質:

1) 范數‖S‖=1/M;

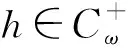
證明: 1) 由S的定義可知,

即‖S‖≤1/M.

另一方面, 取h0=1, 則h0∈Cω(), ‖h0‖C=1, 且于是有

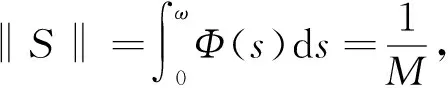
(5)

故性質1)成立.

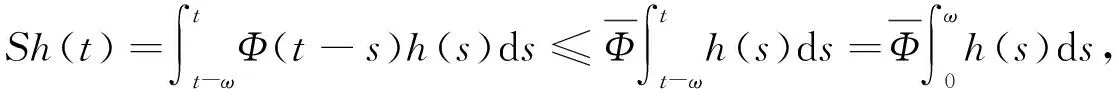
(6)

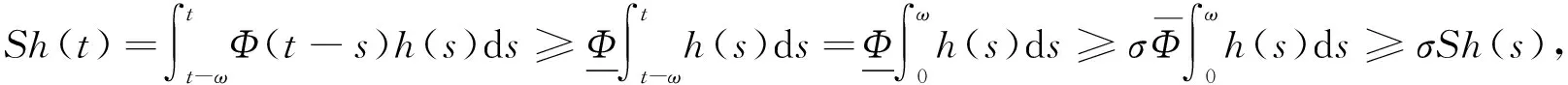
(7)

故性質2)成立. 證畢.

證明： 由線性方程ω-周期解的表示式(3)知,u∈Cω()是方程(4)的ω-周期解當且僅當

(8)

定義算子B:Cω()→Cω()為

(9)

則B:Cω()→Cω()為正的有界線性算子, 易知結合式(3),(8),(9), 有

(I+SB)u(t)=Sh(t),t∈.

(10)

由單位算子擾動理論可知,I+SB為有界線性逆算子：

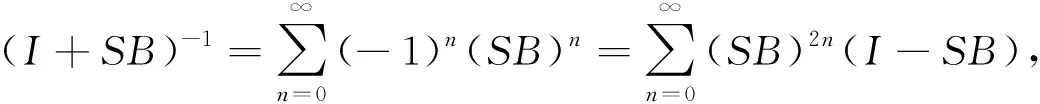
(11)

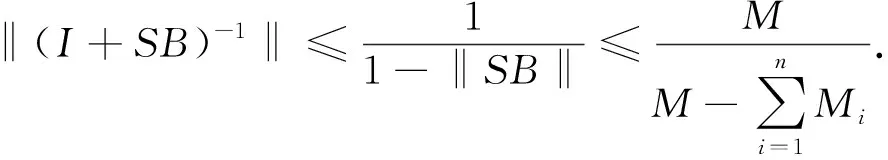
(12)

因此算子方程(10)有唯一解

(13)

其為方程(4)的ω-周期解. 由式(3)知,S:Cω()→Cω()是線性全連續算子, 由(I+SB)-1的有界線性可知,T=(I+SB)-1S是全連續的. 由式(11)～(13)可得

因此(I-SB)S是正的, 即T:Cω()→Cω()是一個正算子. 證畢.

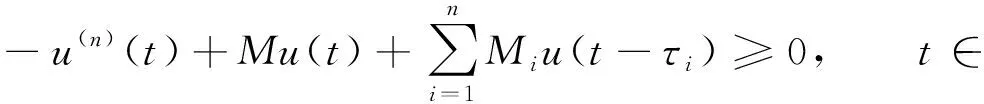
則u(t)≥0,t∈.

證明： 令

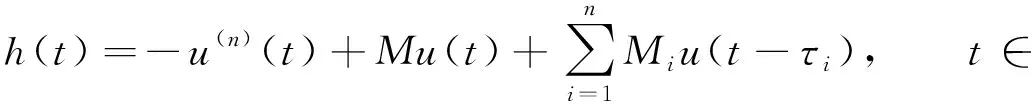
為利用單調迭代技巧, 類似周期邊值問題上下解的概念[10], 本文引入方程(1)上下ω-周期解的定義.

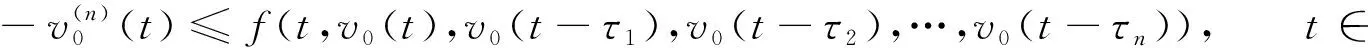
(14)

則稱v0是方程(1)的下ω-周期解; 若上述不等號取反向, 則稱v0是方程(1)的一個上ω-周期解.

2 主要結果

定理1設f:×n+1→連續, 關于t以ω為周期, 且v0和w0是方程(1)的下ω-周期解和上ω-周期解,v0≤w0,v0≤Qv0,Qw0≤w0, 則方程(1)在v0和w0之間存在最小ω-周期解和最大ω-周期解, 且可分別以v0,w0為初始元作迭代得到.

若f在v0和w0之間還滿足以下條件:

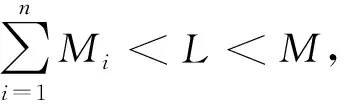
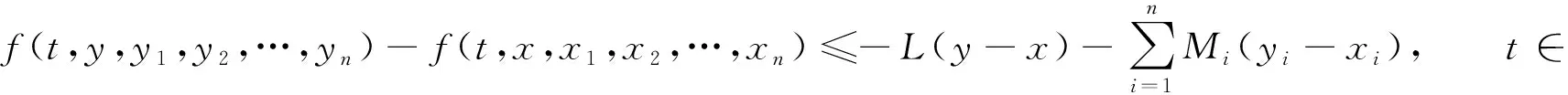
則方程(1)在v0和w0之間存在唯一解u*.

證明： 令D=[v0,w0]={u∈Cω()|v0≤u≤w0}. 定義算子F:D→Cω()為

于是F:D→Cω()連續、有界, 且為增算子. 則方程(1)在D中的解等價于算子Q=T°F:D→Cω()有不動點, 且由F的序增性及T的線性和正性可知Q=T°F是增算子, 即對?u1,u2∈[v0,w0], 滿足u1≤u2, 則Qu1≤Qu2.

對Q用增算子不動點定理單調迭代求解. 下面分三步證明.

1) 證明算子Q在D中有不動點. 分別以v0,w0為初始元作迭代序列:

vn=Qvn-1,wn=Qwn-1,n=1,2,….

(15)

根據算子Q的單調性, 有

v0≤v1≤v2≤…≤vn≤…≤wn≤…≤w2≤w1≤w0,

(16)

則{vn}和{wn}分別在序區間D上單調遞增和單調遞減. 由Q的緊性可知, {vn},{wn}?[v0,w0]為Cω()中的相對緊集, 有一致收斂的子列. 因此{vn}和{wn}均在Cω()中收斂, 即(), 使得又因為D為Cω()中的凸閉集, 故在式(15)中令n→∞, 則由Q的連續性知,所以和都是算子Q在D中的不動點.

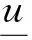
vn≤u*≤wn.

(17)

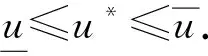
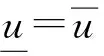
則

‖wn-vn‖C≤(M-L)n·‖Tn‖·‖w0-v0‖C.

(18)

由于{vn}和{wn}在Cω()中分別單調遞增收斂到及單調遞減收斂到所以在式(18)中, 當n→∞時, 有從而即u*是方程(1)在方程v0和w0之間的唯一解. 證畢.