分數階微分方程無窮多點邊值問題正解的存在性
尚 淑 彥
(西北師范大學 數學與統計學院, 蘭州 730070)
0 引 言
分數階微分方程在電磁學、力學、醫學、擴散、控制、信息處理等領域應用廣泛. 目前, 分數階微分方程的研究主要集中在非線性分數階微分方程邊值問題正解的存在性、多重性和唯一性[1-11].
文獻[1]利用Krein-Rutman定理研究了m-點邊值問題:



受上述研究工作啟發, 本文考慮問題

(1)

1 預備知識
定義1[12]函數f: [0,∞)→的α>0階Riemann-Liouville分數積分定義為
定義2[12]函數f: [0,∞)→的α>0階Riemann-Liouville分數導數定義為

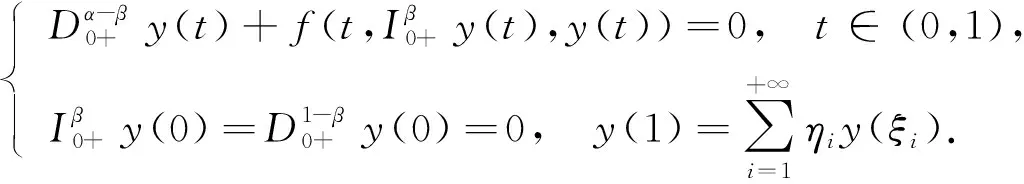
(2)
由文獻[5]知, 增函數
有唯一的根τ*>0.
顯然, 共振問題(2)等價于非共振問題:

(3)
其中τ∈(0,τ*],τ<1. 記

(4)
引理1設g∈C[0,1], 則分數階邊值問題

(5)
有唯一解
證明:y(t)的證明過程與文獻[3]類似, 故略. 下面證明
收斂. 由式(4)得

(6)
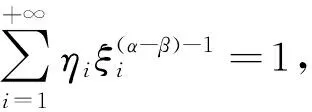
由于
故G(1)在[0,1]上收斂.G(1)各項絕對值組成的級數為
用比式判別法可得
因此|G(1)|收斂, 從而G(1)絕對收斂. 記

用比式判別法可得


收斂.
記K(s)=(1-s)α-β-2-s在[0,1]上嚴格遞減, 且K(0)=1,K(1)=-1, 則K(s)在(0,1)上有唯一的根s*, 滿足
s*=(1-s*)α-β-2.
引理2H(t,s)有下列性質:
ρ1s(1-s)α-β-1tα-β-1≤H(t,s)≤ρ2s(1-s)α-β-1,t,s∈[0,1],
其中
引理2的證明過程與文獻[3]類似, 故略.
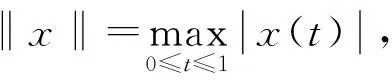

1) ‖Ax‖≤‖x‖, ?x∈P∩?Ω1; ‖Ax‖≥‖x‖, ?x∈P∩?Ω2;
2) ‖Ax‖≤‖x‖, ?x∈P∩?Ω2; ‖Ax‖≥‖x‖, ?x∈P∩?Ω1.

設P是Banach空間E中的一個錐,Pr={x∈P|‖x‖ 考慮P上一個非負連續凹泛函α(x), 即α:P→[0,∞)連續, 且對?x,y∈P, 0≤t≤1, 有 α(tx+(1-t)y)≥tα(x)+(1-t)α(y). 下面恒用P(α,a,b)表示集合{x∈P|a≤α(x), ‖x‖≤b}, 這里0 1) {x|x∈P(α,b,d),α(x)>b}≠?, 且當x∈P(α,b,d)時, 恒有α(Ax)>b; 3) 當x∈P(α,b,c)且‖Ax‖>d時, 恒有α(Ax)>b. 注1如果d=c, 則由引理4中條件1)可推出條件3). 設 引理5[3]設算子A:Q→E定義為 則A:Q→Q是全連續的. 為方便, 記 定理1令g(t,x,y,τ)=f(t,x,y)+τy, 設存在兩個正數r2>r1>0, 使得下列條件成立: 則問題(1)至少存在一個正解, 且r1<‖y‖ 證明: 記Ω1={y∈Q|‖y‖≤r1}, 對y∈?Ω1, 有0 因此 ‖Ay‖≥‖y‖, ?y∈Q∩?Ω1. 記Ω2={y∈Q|‖y‖≤r2}, 對y∈?Ω2, 有0 因此 ‖Ay‖≤‖y‖, ?y∈Q∩?Ω2. 由引理3可知, 問題(1)至少存在一個正解, 且r1≤‖y‖≤r2. 證畢. 對?R≥r>0, 定義 定理2假設存在0 則問題(1)至少存在3個正解y1,y2,y3. 首先, 設{xn?Q},x∈Q且xn→x(n→∞), 即 因為 且 所以 從而 故α是連續泛函. 其次, ?x,y∈Q,α:Q→[0,∞)連續, 0≤λ≤1, 有 顯然α(x)是在Q上的非負連續凹泛函, 且α(x)≤‖x‖. 對t∈[δ,1-δ], 有 則引理4中條件1)成立. 3) 證明引理4中條件3)成立. 對?y∈Q(α,b,c), 有‖Ay‖≥d,dx*>b.因此 綜上, 本文分別用錐拉伸與壓縮不動點定理和Leggett-Williams不動點定理, 得到了問題(1)至少存在1個正解和3個正解的結果. 特別地, 在Leggett-Williams不動點定理中, 對問題(1)中的非線性項f的限制更多則條件更強, 得到的結果相比于錐拉伸與壓縮不動點定理的結果更好.
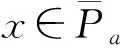


2 主要結果










