基于廣義S變換和隨機子空間的局放窄帶干擾抑制方法

宋立業， 蒲霄祥， 李希桐

(遼寧工程技術大學電氣與控制工程學院， 遼寧 葫蘆島 125105)

1 引言

局部放電(Partial Discharge，PD)監測是有效診斷電力電纜絕緣狀態的手段之一，一般情況下PD的信號能量較弱，會被現場的電磁干擾所掩蓋，阻礙了PD信號的提取識別[1,2]。PD信號面臨的電磁干擾主要分為隨機脈沖干擾、周期性窄帶干擾和白噪聲三大類，其中周期性窄帶干擾擁有噪聲能量強和持續時間長的特點，會嚴重污染PD信號，因此研究PD信號中窄帶干擾抑制方法具有重大的意義[3]。

目前，國內外學者針對PD信號的窄帶干擾抑制方法開展了大量研究。文獻[4]提出利用快速傅里葉變換配合頻域中閾值抑制窄帶干擾，該方法操作簡單、計算速度快，但是容易受到頻譜泄露的影響造成嚴重的邊緣效應。文獻[5,6]提出利用小波分解方法開展PD信號去噪，該方法可以有效分析PD信號的時頻特征，進而取得較好的去噪效果，但是該方法需要人為設定小波基、分解層數和各層閾值，去噪效果受人為因素影響較大。文獻[7]提出利用經驗模態分解方法對PD信號進行自適應分解去噪，該方法不需要選擇基函數，能更好地適應多種PD信號，但是該方法存在端點效應和模態混疊的問題。文獻[8,9]提出利用奇異值分解實現窄帶干擾和PD信號的分離，該方法僅需要確定奇異值閾值便可以重構出純凈的PD信號，但是該方法難以準確給出奇異值閾值，同時該方法在窄帶干擾幅值較低以及干擾和PD信號的頻率出現混疊時去噪效果較差。

廣義S變換具有良好的時頻分辨能力，能有效地分離出時頻特征不同的PD信號和窄帶干擾，因此被逐漸用于PD信號的窄帶干擾抑制中。文獻[10]提出利用廣義S變換模時頻矩陣的能量分布重構窄帶干擾進行去噪，該方法可以有效在時頻域中分離出PD信號和窄帶干擾，但是沒有考慮窄帶干擾相位的影響。文獻[11]提出利用廣義S變換配合奇異值分解算法實現窄帶干擾抑制，雖然解決了奇異值分解算法中奇異值閾值的選取問題，但是仍在窄帶干擾和PD信號的頻率出現混疊時去噪效果較差。

綜上所述，本文提出一種基于廣義S變換和隨機子空間的局部放電窄帶干擾抑制方法。該方法首先通過廣義S變換得到染噪PD信號的模時頻矩陣，然后根據窄帶干擾和PD信號各自的時頻特征確定窄帶干擾數量和分離出不含PD的時間片段，接著利用隨機子空間算法進行窄帶干擾數據重構，最后提取出純凈的PD信號。分別利用本文方法、廣義S變換模矩陣方法和頻率切片小波變換方法對仿真和實測的染噪PD數據進行窄帶干擾抑制，對比結果顯示，相比于傳統方法，本文方法能更好地抑制局部放電信號中的窄帶干擾。

2 算法原理

2.1 廣義S變換

S時頻變換早期由Stockwell提出，該方法集合了短時傅里葉變換和連續小波變換的優點[10,11]。S變換中窗函數選用了參數可變的高斯函數，該函數的時寬和頻率成反比，幅值與頻率成正比，因此S變換可以在低頻區間獲得較好的頻率分辨率，而在高頻區間獲得較好的時間分辨率，擁有優異的時頻分析能力，對于提取PD信號這類非平穩信號的時頻分布特征具有良好的效果。

信號y(t)的S變換可以表示為:

(1)

式中,f為頻率；ω(t-τ,f)為高斯窗函數；t、τ為時間變量。

S變換中窗函數表達式為：

(2)

從式(2)中可以看出，S變換中窗函數的幅值和時寬是隨頻率變化而變化的，因此S變換中時頻分辨率能夠跟隨頻率變化而變化，能改善短時傅里葉變換中不變的時頻分辨率，同時不需要考慮連續小波變換中基函數的選擇問題，憑借上述優點，S變換具有良好的使用前景。

為了使S變換能夠適用更多的使用場景，Pinnegar設計了調節因子λ(λ>0)對S變換中高斯窗函數進行了改進[10,11]，得到新的窗函數為：

(3)

使用式(3)作為窗函數的S變換被稱為廣義S變換，從式(3)中可以看出，廣義S變換可以通過調節λ實現高斯窗函數和f的變化率調節。當λ<1時，高斯窗的時寬增加，幅值減少，廣義S變換的頻率分辨率增加，時間分辨率下降；當λ>1時，高斯窗的時寬減少，幅值增加，廣義S變換的頻率分辨率下降，時間分辨率增加，由此實現時頻分辨率的有效調節。

由于實際信號通常為離散數據，因此需要對廣義S變換做離散化處理，令f=n/(NT)和τ=iT，其中T為采樣周期，N為采樣個數，得到離散的廣義S變換為：

(4)

式中，n，i=0，1，…，N-1；Y是y的傅里葉系數。

通過式(4)得到信號的廣義S變換復數矩陣。為了能直觀分析信號在時頻域中的能量分布，對該復數矩陣進行求模，得到廣義S變換模矩陣(Generalized S-transform Modular Matrix，GSMM)。該矩陣能直接反映信號能量的時間和頻率分布特性，因此可以利用GSMM對信號的時頻特征進行深度分析。

2.2 隨機子空間

隨機子空間算法可以有效地計算離散系統的模態參數，并且有著計算精度高、受采樣條件影響小和步驟簡單的優點[12]。其中基于協方差驅動的隨機子空間算法憑借著優異的計算效率被廣泛使用[13]，本文將其引入用于窄帶干擾參數估計。

將離散信號yk以離散系統的狀態方程可以表示為：

(5)

式中，A為離散系統的狀態矩陣；C為離散系統的輸入矩陣；xk和yk分別為離散系統k時刻的狀態量和輸出量；wk為離散系統中白噪聲；vk為測量中白噪聲。對應本文中，yk是離散的窄帶干擾信號。

將yk建立三個時間矩陣分別為：

(6)

(7)

(8)

式中，Yp為“過去”時間矩陣；Yf1為第一個“未來”時間矩陣；Yf2為第二個“未來”時間矩陣；b為時間矩陣的列數，該值越大，說明離散系統輸出數據量越多，此時各參數估計越精準，但是yk的數據量是有限的，因此本文取b>10(N-b-1)，得到b為：

b=Floor(10(N-1)/11)

(9)

式中，Floor是向下取整。

將三個時間矩陣Yp、Yf1和Yf2構建托普利茨矩陣T1和T2為：

T1=Yf1YpT

(10)

T2=Yf2YpT

(11)

接著將T1開展奇異值分解為：

(12)

式中，S1、S2分別為信號和噪聲主導的奇異值對角矩陣；U1、U2分別為信號和噪聲主導的左單位奇異矩陣；V1、V2分別為信號和噪聲主導的右單位奇異矩陣。

從統計理論上分析，wk和vk應該是無相關性的兩組噪聲，由此根據離散系統的理論可得：

(13)

式中，Oa為觀測矩陣；G=E(x(k+1)ykT)，E為期望；Гa為控制矩陣；a=N-b-1。

將式(12)和式(13)進行聯合分析可得：

(14)

再依據式(13)可得：

T2=OaAΓa

(15)

進一步聯合式(14)和式(15)得到A為：

(16)

對A開展特征值分解為：

A=ψΛψ-1

(17)

式中，Λ=diag(zs)，s=1，2，…，p；zs是A的第s個特征值；p為式(5)中系統的階數，對應本文為窄帶干擾個數的2倍；ψ為A的特征矩陣。

利用最小二乘法求解下式即可得到參數Bs。

(18)

利用zs和Bs得到窄帶干擾的幅值Qs、頻率fs和相位θs分別為：

Qs=2|Bs|

(19)

(20)

(21)

由于窄帶干擾為實信號，因此確定fs>0的對應數據組為真實數據，進而估計得到窄帶干擾的幅值、頻率和相位。

2.3 PD窄帶抑制流程

本文結合廣義S變換和隨機子空間提出PD窄帶干擾抑制方法的具體步驟為：

(1)將染噪PD信號開展廣義S變換，得到對應的廣義S變換模矩陣GSMM。

(2)借助窄帶干擾時間分布長，頻率能量集中的特點確定窄帶干擾個數。

(3)借助PD信號時間分布短，頻率能量分布寬的特點確定染噪PD信號中無PD的最長時間片段。

(4)利用隨機子空間算法對染噪PD信號中無PD的最長時間片段進行處理，估計窄帶干擾參數。

(5)利用估計的窄帶干擾參數值對窄帶干擾信號進行重構，在時域中將染噪PD信號減去窄帶干擾的重構值，得到窄帶干擾抑制后的PD信號。

3 仿真測試

3.1 仿真局放模型

PD信號通常呈現衰減振蕩的特性，因此可以用如式(22)和式(23)所示的單指數衰減振蕩型和雙指數衰減振蕩型信號模型進行模擬[14]。

g1(t)=Ce-t/ηsin(2πfgt)

(22)

g2(t)=C(e-1.3t/η-e-2.2t/η)sin(2πfgt)

(23)

式中，C為脈沖幅值；η為衰減系數；fg為振蕩頻率。

本節模擬4個PD脈沖信號，各脈沖信號參數如表1所示，其中脈沖Ⅰ和Ⅲ是單指數衰減振蕩型脈沖，脈沖Ⅱ和Ⅳ是雙指數衰減振蕩型脈沖，采樣頻率為30 MHz。

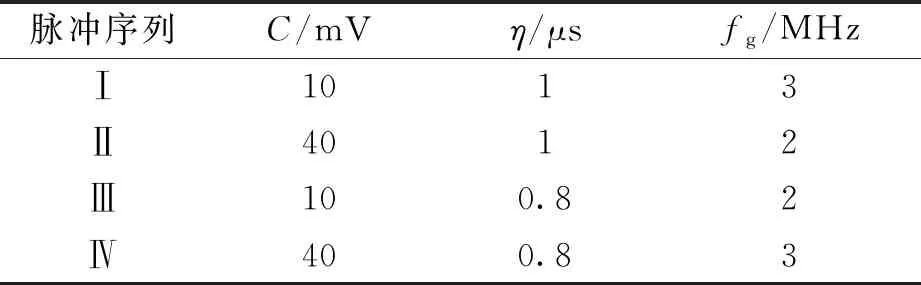
表1 仿真PD脈沖參數

仿真中窄帶干擾由4個不同頻率、幅值和初始相位的正弦波疊加組成，根據文獻[11、15]的仿真窄帶干擾參數范圍，本文將仿真中窄帶干擾的參數值設置如表2所示。由此得到純凈的PD信號、窄帶干擾信號和染噪PD信號如圖1所示。從圖1中可以看出，在染噪PD信號中，由于窄帶干擾的存在，PD信號幾乎完全被淹沒，難以直接進行識別和提取。

表2 仿真窄帶干擾參數

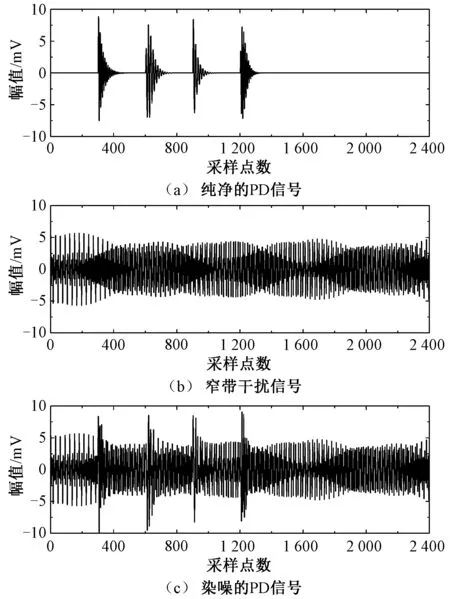
圖1 仿真的PD信號

3.2 局放去噪

由于廣義S變換仍屬于短時傅里葉變換，因此其時間分辨率和頻率分辨率并不能同時達到最高，本文將λ取為0.4以同時獲得較好的時間分辨率和頻率分辨率。通過廣義S變換處理圖1(c)中的染噪PD信號，得到染噪PD信號的GSMM如圖2所示。從圖2中可以看出窄帶干擾信號和PD信號存在明顯不同的特征：窄帶干擾信號時間上分布較長，頻率上分布較集中；PD信號時間上分布較短，頻率上分布較寬。

以此可以通過分析圖2中染噪PD信號的GSMM確定窄帶干擾的個數為4，同時可以在時間橫軸上進行區域劃分，得到無PD區域。對于圖2而言，橫軸上采樣點數為1 400～2 400區域可以被視為無PD區域，該區域中主導信號為窄帶干擾信號。將最長時段的無PD區域作為窄帶干擾參數估計時間段，選擇圖1(c)中染噪PD信號中該時間段的數據進行隨機子空間算法處理，得到窄帶干擾參數估計值如表3所示。對比表2和表3可以看出，該方法可以有效地估計窄帶干擾的各參數值。值得說明的是，由于僅截取了染噪PD信號中部分時段區段進行參數估計，因此估計得到的相位和原始參數的相位是不一致的。

表3 仿真染噪PD信號的窄帶干擾參數估計值

利用表3中窄帶干擾參數估計值重構整個時間段的窄帶干擾，重構的窄帶干擾Dg如下：

(24)

式中，t1為截取區段的起始時刻。

將染噪PD信號減去重構的窄帶干擾得到去噪結果如圖3(a)所示，為了進行對比，利用廣義S變換模矩陣方法[10]和頻率切片小波變換方法[16]處理圖1(c)中染噪PD信號，得到去噪結果分別如圖3(b)和圖3(c)所示。從圖3的對比結果可以看出，對于廣義S變換模矩陣方法而言，該方法沒有考慮窄帶干擾相位的影響，因此對于本文中窄帶干擾相位不為0的情況，該方法無法實現窄帶干擾抑制；對于頻率切片小波變換方法而言，去噪后波形存在較大殘余噪聲，同時波形中存在明顯的邊緣效應，整體去噪效果較差；本文方法去噪后波形的噪聲較小，PD信號的細節得到保留，利于后續PD信號的提取識別分析。

圖3 仿真染噪PD信號的窄帶干擾抑制結果

為了進一步說明3種方法的去噪效果，本文引入信噪比SNR、均方誤差MSE和波形相似度NCC三個評價參數開展分析[17]，其具體計算公式為：

(25)

(26)

(27)

式中，g(n)為原始PD信號；d(n)為各方法去噪后的信號。其中SNR越大，MSE越小，NNC越接近于1時，去噪效果越好。

計算得到圖3中各方法去噪后波形的SNR、MSE和NCC如表4所示，從表4中可以看出，和廣義S變換模矩陣方法、頻率切片小波變換方法相比，本文方法能更好地去除染噪PD信號中窄帶干擾，去噪后波形更好地保留了原始PD信號的波形特征，利于后續的分析研究。

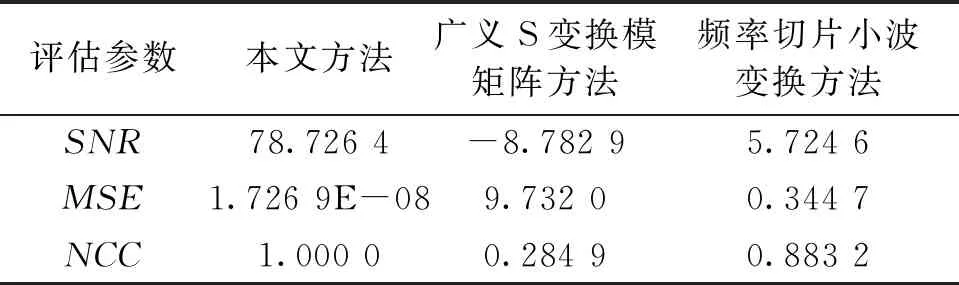
表4 窄帶干擾抑制結果對比

4 實測研究

為了驗證本文方法在實際測試中的可行性，在實驗室中對10 kV電纜開展工頻局放測試，電纜終端頭中制作有半導電層突刺缺陷[18]，監測方法為高頻電流法[7]，采樣率設置為200 MHz，其具體接線圖如圖4所示。

圖4 工頻局放測試接線圖

由于實驗室中采集的PD信號噪聲較小，因此在采集的PD信號中添加多個窄帶干擾信號。文獻[19]指出高頻電流法受到的窄帶干擾主要包括中波段0.5～1.6 MHz、短波段 2.3～25 MHz和調頻段88～108 MHz的廣播信號。因此本文在此基礎上隨機選擇窄帶干擾信號的幅值分別為2 mV、4 mV、3 mV和2 mV；頻率分別為5.06 MHz、10 MHz、15.18 MHz和22 MHz；相位分別為π/4 rad、π/3 rad、π/5 rad和π/2 rad，得到實測的染噪PD信號如圖5所示，從圖5中可以看出，由于窄帶干擾的污染，PD信號無法直接被識別提取。

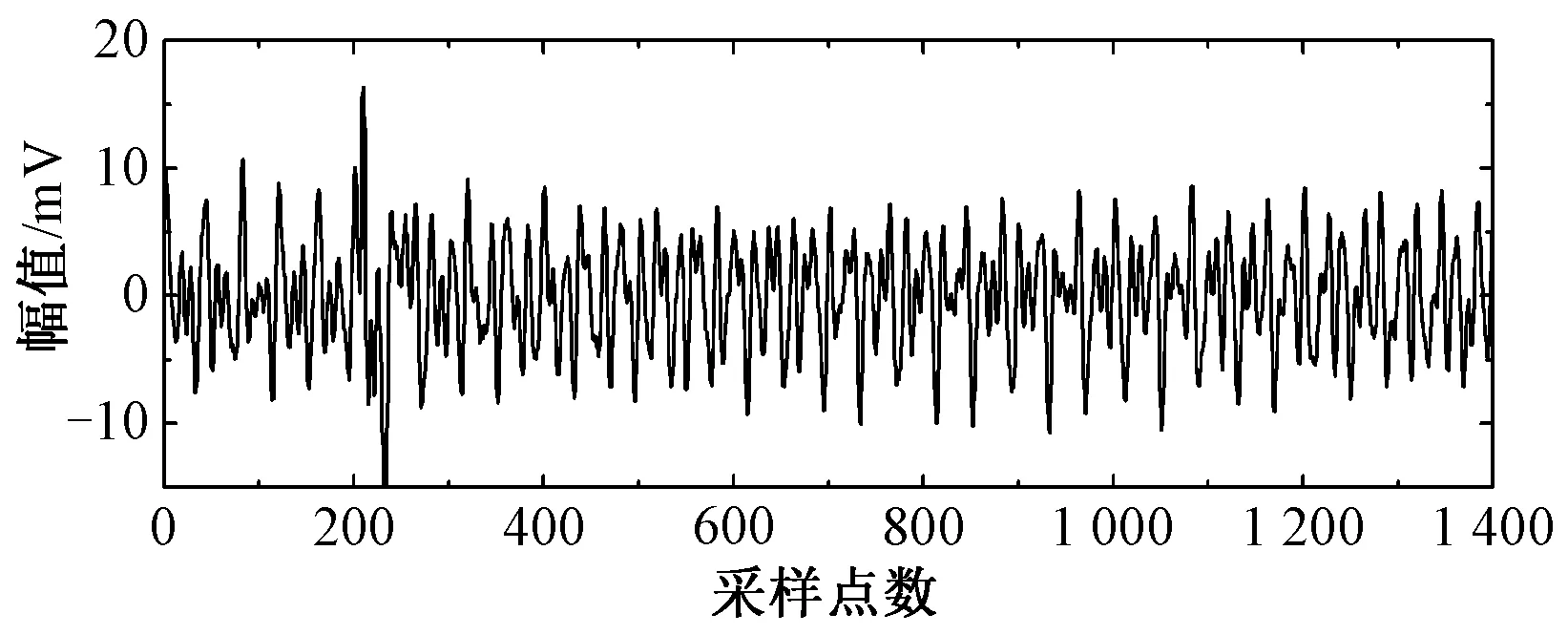
圖5 實測的染噪PD信號

利用本文方法對圖5中染噪PD信號進行去噪處理，得到染噪PD信號的GSMM圖如圖6所示，借助PD信號和窄帶干擾的時頻特征，可以確定圖6中窄帶干擾數目為4，同時很容易在時間橫軸上確定無PD區域。對于圖6而言，時間橫軸上采樣點數為600～1 400區域可以被視為無PD區域，將圖5中染噪PD信號對應時間段的數據利用隨機子空間算法進行窄帶干擾參數估計，得到窄帶干擾參數估計結果如表5所示，利用該結果對窄帶干擾進行重構，得到去噪后波形如圖7(a)所示。為了進一步說明本文方法的優越性，再利用廣義S變換模矩陣方法和頻率切片小波變換方法對圖5中染噪PD信號進行去噪，得到對應去噪結果如圖7(b)和圖7(c)所示。從圖7的對比結果中可以看出，廣義S變換模矩陣方法抑制窄帶干擾失敗，沒有提取出局放波形；頻率切片小波方法的去噪結果中存在明顯的窄帶干擾抑制不干凈現象，同時存在明顯的邊緣效應，因此上述2種傳統方法的去噪效果較差。相對于傳統方法而言，本文方法可以更加有效地提取出PD波形，殘余噪聲更小。

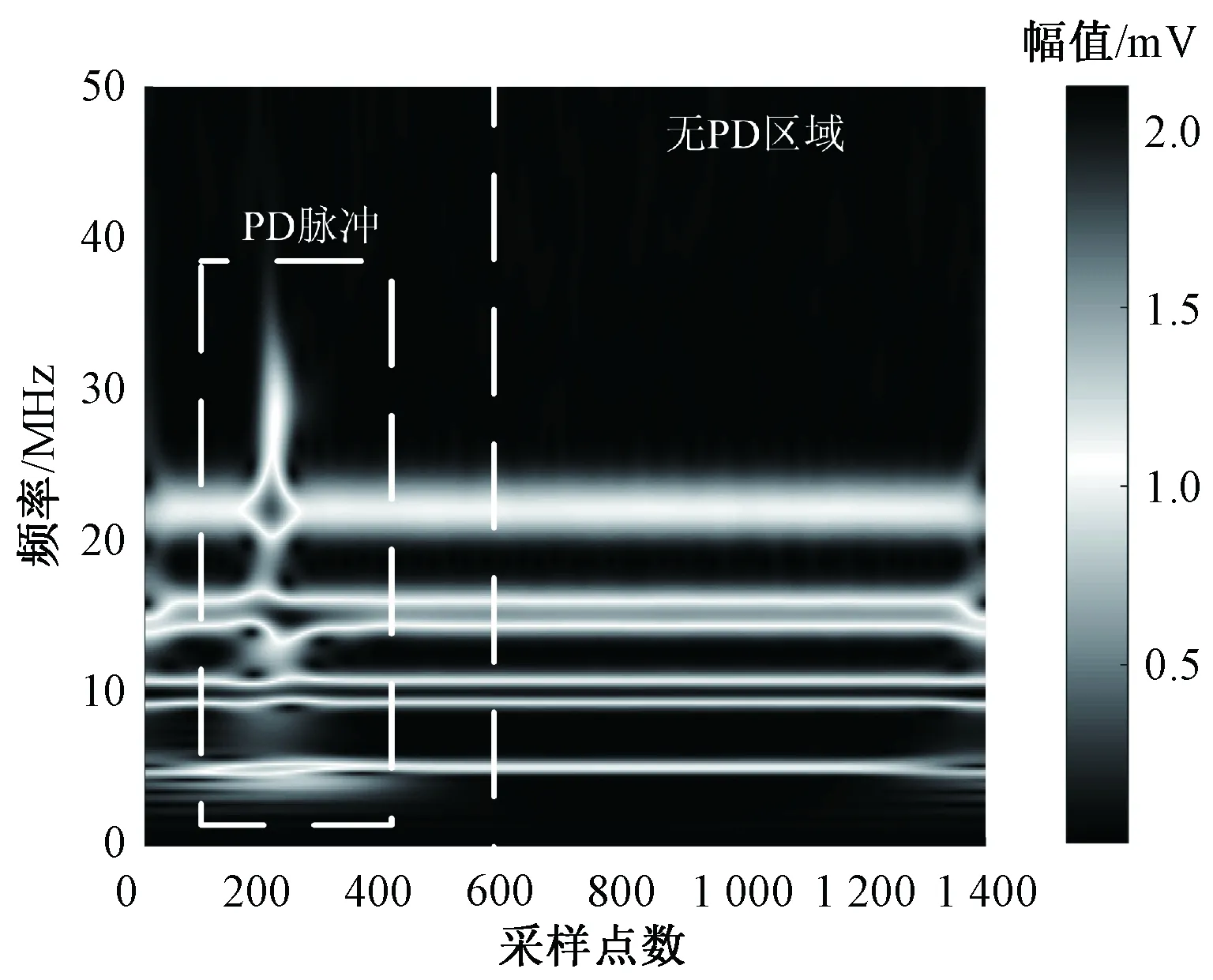
圖6 實測染噪PD信號的GSMM圖

表5 實測染噪PD信號的窄帶干擾參數估計值

圖7 實測染噪PD信號的窄帶干擾抑制結果

為了對圖7中降噪結果進行量化分析，本文引入了噪聲抑制比ρ[9]如式(28)所示。噪聲抑制比可以顯示出窄帶干擾抑制前后有效信號的凸顯程度，該值越大，說明窄帶干擾抑制結果越好。

(28)

式中，σ1和σ2分別為窄帶干擾抑制前、后的信號標準差。

通過計算得到圖7中3種方法的噪聲抑制比分別為10.541 1、-2.854 8和8.188 0，可見，本文方法的噪聲抑制比最大，對窄帶干擾的抑制結果最好。

5 結論

(1)廣義S變換能夠將染噪PD信號從時域轉化到時頻域中，并具有較好的時頻分辨能力，借助PD脈沖和窄帶干擾的不同時頻特征可以確定染噪PD信號中窄帶干擾數目和無PD時間片段。

(2)利用隨機子空間算法和窄帶干擾數目處理無PD時間片段可以精確估計窄帶干擾參數，進而有效重構染噪PD信號中窄帶干擾，對染噪PD信號實現窄帶干擾抑制。

(3)仿真和實測結果表明，相比于廣義S變換模矩陣方法和頻率切片小波變換方法，本文所提方法能夠有效抑制染噪PD信號中的窄帶干擾，去噪后殘余噪聲較小，PD波形恢復效果更好。