考慮脈沖負載影響的直流微電網變換器模型預測控制策略

趙新寬， 陳燕東， 姚 鵬， 姜洪朝

(1. 珠海城市職業技術學院珠海市智能電網技術協同創新中心， 廣東 珠海 519000； 2. 湖南大學國家電能變換與控制工程技術研究中心， 湖南 長沙 410082； 3. 珠海萬力達電氣 自動化有限公司， 廣東 珠海 519000； 4. 中國電子信息產業集團有限公司第六研究所， 北京 102209)

1 引言

隨著電力電子技術的發展，直流微電網相關技術將成為未來新能源接入、全電飛機或船舶的核心關鍵架構。直流微電網能提供高效且可靠的配電，并通過簡單控制對能量進行靈活管理[1-3]。對于全電船舶而言，負載類型較為多樣，包含常規負載、推進負載、脈沖負載(Pulsed Power Load，PPL)和專用高功率負載等[4,5]。其中PPL會間歇性從電網中消耗大量功率，具有一種高功率脈沖行為特性，可能導致電網電壓波動和跳變，甚至導致整個直流微電網失電[6,7]，故對系統運行和控制提出了很高的要求。對此，直流微電網中設置基于電池組或超級電容的儲能系統(Energy Storage System，ESS)可對PPL進行關鍵條件下的補償，從而提高系統可靠性和效率[8-10]。

通常增加電池組儲能的主要方法是增加電池數量，故功率成本折中和電流均分問題使得其不是最理想補償PPL的方案。而超級電容由于其內阻低、功率密度高和循環壽命長，是一種對電池組較好的儲能補充，可形成混合ESS方案[11-13]。混合ESS方案下，PPL暫停時，超級電容平滑充電，而在PPL工作時，其快速放電進行功率緩沖。文獻[14]指出混合ESS可減少內部損耗，并增加ESS的壽命，故較單電池組具有更好的性能。混合ESS若直接接入直流側，則稱為無源混合ESS，其優點是成本低和損耗小。但電池組和超級電容直接并聯連接會限制兩者之間的功率均分，故可設置變換器接入到直流側，則該配置稱為有源混合ESS。文獻[15]中指出有源混合ESS可通過變換器調節功率流，故可使得ESS體積容量更小。由于有源混合ESS經由變換器接入直流側，故需分析系統穩定性和進行協調控制策略設計[16-18]。同時，構建的控制方案必須能考慮PPL、ESS和系統之間的交互來減輕PPL的不利影響[19]。文獻[20]提出了混合直流儲能的瞬時功率控制方案，并在直流母線上配備了電壓滯環保護。文獻[21]中提出基于極限電壓的控制結構，可根據變換器功率和電源可用功率的限制，控制直流電壓盡可能快地為ESS充電。文獻[22，23]設計了一種平均電流控制方案，其試圖將變換器輸出電流盡量保持恒定以減輕對變換器和ESS的影響。文獻[24，25]中利用自適應補償器和滑動平均測量技術設計了電流-電壓協調控制方案，可實現對變流器電流和直流電壓的同時控制。但上述方案均沒有考慮ESS電壓限制問題，也忽略了系統硬約束。

目前，隨數字芯片發展，模型預測控制(Model Predictive Control，MPC)在電力電子變換器中的應用前景趨于廣闊[26,27]。MPC可通過最優化成本函數計算直接獲取變換器控制信號來實現最優控制。故本文將MPC引入到直流微電網變換器控制中，實現了一種簡單、魯棒性好且高效的直流微電網控制策略。不同于傳統控制方法，所設計的控制系統不僅考慮了系統硬約束，還具備將直流微電網輸出電壓和電流保持在工作點附近較小區域中的能力，同時還保證了超級電容快速充電，以應對PPL的不利影響。最后，通過實驗驗證了所設計MPC方案的效果。

2 直流微電網配置及其動態建模

本文研究對象為全電船舶直流微電網[28]，如圖1所示，包含發電機組、混合ESS、PPL、推進負載和常規負載等。其中混合ESS用于補償直流側的電壓波動。此外，還有能量管理控制系統參與進行分散式或集中式的系統能量調度和控制，實現在一些預定目標下優化系統運行。直流微電網中還配備有系統保護，由變換器控制和直流斷路器組合實現，以應對系統故障。

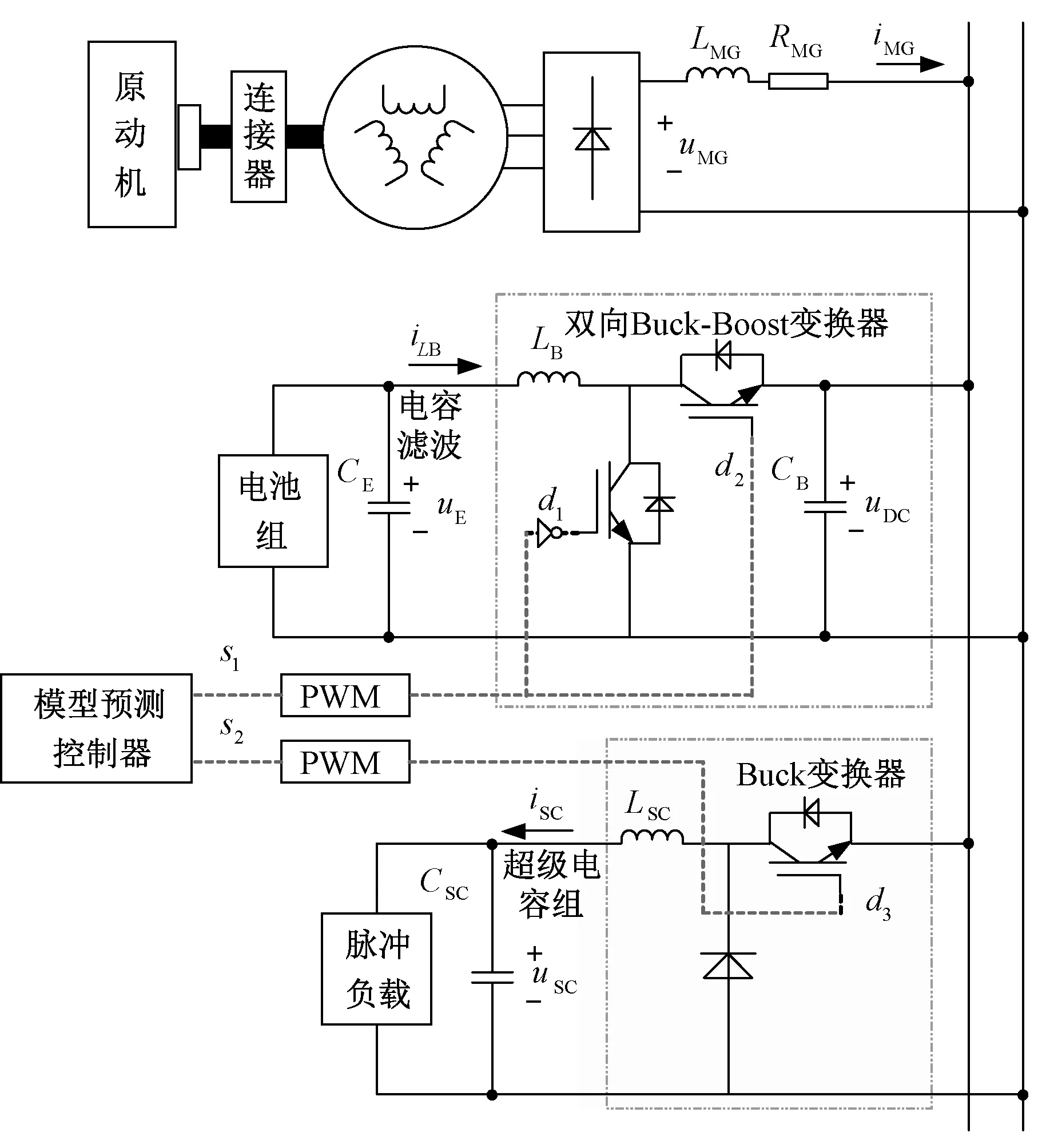
圖1 直流微電網配置

2.1 直流微電網配置

圖1中直流微電網的電源由三相同步發電機組及不控整流器組成，整流器輸出電壓為uMG。混合ESS包含超級電容和電池組，分別經Buck變換器和雙向Buck-Boost變換器接到直流側[29]。在孤島模式或高負載等工況下，電池組可為直流電壓提供長期支持；而在正常情況下電池組將進行充電。此外，PPL通過功率緩沖器連接到直流母線，功率緩沖器即由超級電容組成，超級電容通過直流側充電后斷開連接，當PPL激活時，其迅速放電以達到功率緩沖的目的。

2.2 ESS動態模型

圖2(a)為鋰離子電池組的經典電路模型[30]。圖2(a)中，Rp和Cp分別是極化電阻和電容。電池組的充電狀態可定義為：

(1)

式中，SOC為電池組荷電狀態；CESS為電池組標稱容量；ib為負載電流；kt為充電系數。對式(1)進行微分運算可得：

(2)

式中，Rb為電池組內阻；uE為輸出電壓；up為極化電容電壓；uoc是電池組內電壓。將圖2(a)中電路模型結合雙向Buck-Boost變換器電路可得圖2(b)中的電池組接入直流側電路模型。結合圖1，可推導得到混合ESS的狀態空間模型為：

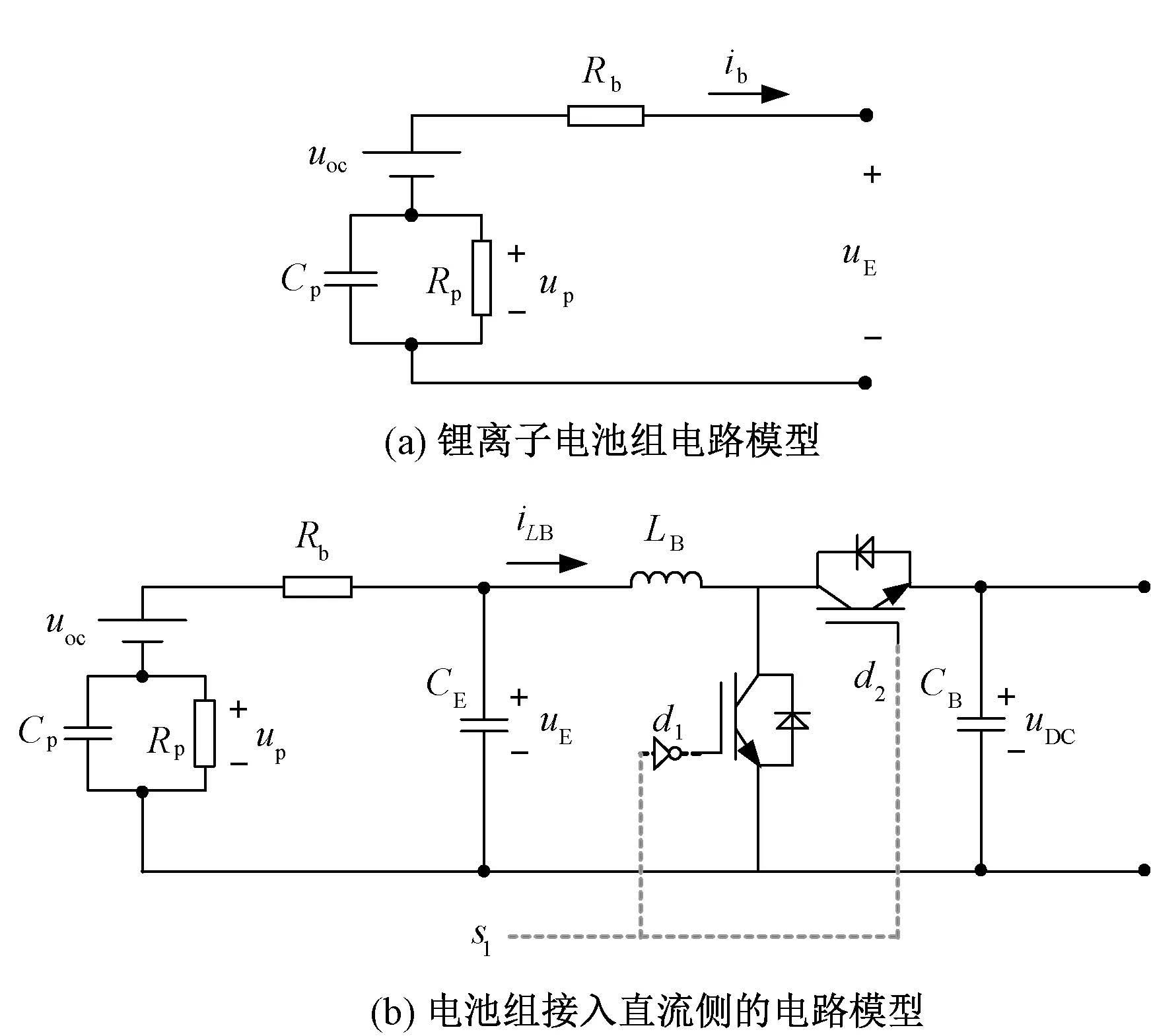
圖2 ESS電路模型

(3)

式中，s1和s2分別為雙向Buck-Boost變換器和Buck變換器的控制信號；LB和CE分別為雙向Buck-Boost變換器電池側電感和電容；CB為雙向Buck-Boost變換器直流母線側電容；RLB為LB的寄生電阻；iLB為流過LB的電流；uDC為直流母線電壓；iSC為Buck變換器內電感LSC上電流；iMG為直流源輸出電流。

2.3 PPL動態模型

圖3所示為ESS及其功率緩沖器的電路模型。考慮到PPL突然需要較高的功率，因此設置了超級電容由Buck變換器接入到直流側進行緩沖。根據圖3，可推導得PPL的狀態空間模型為：

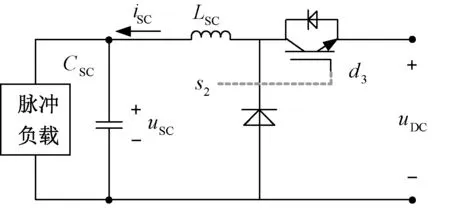
圖3 PPL電路模型

(4)

式中，CSC為超級電容的容值；uSC為CSC上的電壓；LSC為Buck電路內電感；RSC為LSC的寄生電阻；PPL(t)為脈沖負載功率。

2.4 直流源動態模型

如圖4所示為直流源電路模型，據此可推導得到直流源的狀態空間模型為：

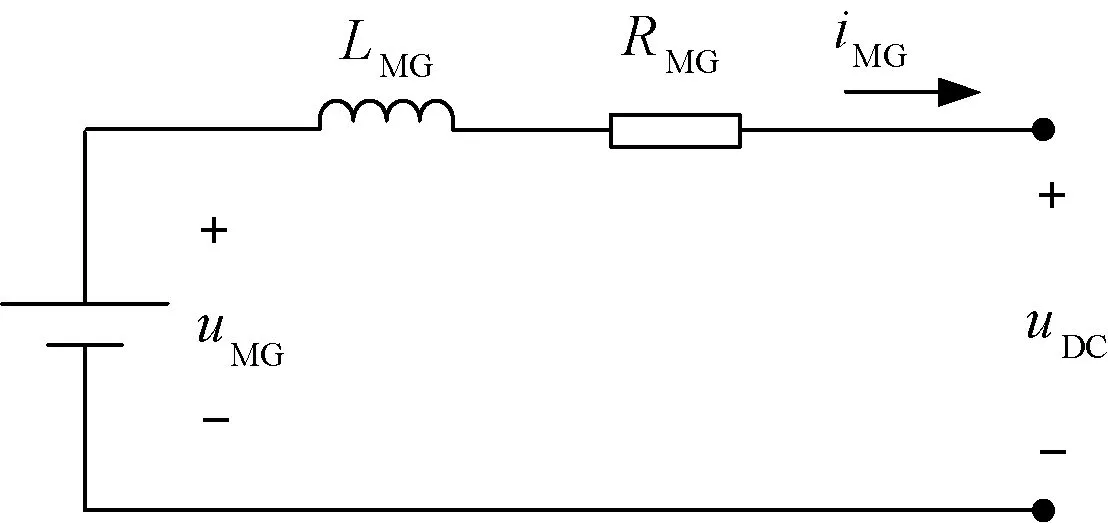
圖4 直流源電路模型

(5)

式中，RMG和LMG分別為對直流側電壓的壓降進行模擬而設置的電源內阻和內電感；uMG和iMG分別為直流源輸出電壓和電流。

2.5 直流微電網的動態模型

根據前述對直流微電網中各組成部分的建模及其狀態空間模型推導，可構建出整個直流微電網的狀態空間模型。設z=[z1z2z3z4z5z6z7z8]T=[uEupuDCiLBuSCiSCiMGSOC]T，而脈沖負載功率PPL(t)為未知擾動d(t)，聯立式(3)～式(5)可得直流微電網的狀態空間模型為：

(6)

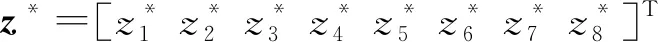
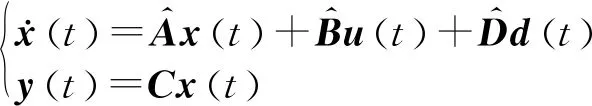
(7)

其中

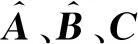
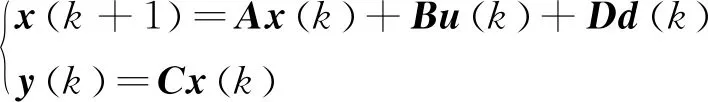
(8)

式中，A、B、C和D為離散模型中的常系數矩陣；k為步長。

3 系統約束分析

圖1中所示直流微電網配置可在極端工況條件下，使系統運行能力最大化。根據1～35 kV中壓直流電網標準[28]，在設計控制策略時需考慮系統約束，以保證輸出電能質量。圖1中直流微電網各個設備均由電力電子變換器連接到直流側，因此需進行協調控制。此外，通過使用主動配置可以限制故障電流。根據圖1中系統配置，可以提取出主要的系統約束如下：①發電機組是通過不控整流器實現交流電能向直流側的輸送，輸出電流為iMG，其中不控整流器中必須使用半導體限流裝置；②需確保直流母線電壓uDC在允許范圍內；③由于直流變換器存在電流限制，即iLB和iSC存在最大限制，故過電流保護是必要的；④超級電容電壓uSC需控制為較高且相對穩定，以補償PPL高脈沖功率的影響；⑤變換器由PWM調制器生成的0/1脈沖信號進行控制。下面設計MPC方案時將考慮上述所有列出的系統約束。

4 直流微電網變換器MPC方案設計

MPC廣泛用于各類工業場景中，可很好地解決帶約束的控制問題。MPC方法較傳統控制技術具有優勢如下：①可處理多輸入多輸出系統；②可對輸入輸出信號嚴格限幅；③MPC方法可用于包括延遲、不確定性或擾動的非線性系統。

MPC方案設計的關鍵在于求解約束下的最優化問題，這需要基于系統模型計算狀態變量和控制信號在預測范圍內的演變，并在每個步長得到使預測結果最優的控制信號施加到系統中。由于MPC中最優問題的結構可以轉換為凸結構，因此可以使用線性矩陣不等式方法進行數值求解。

對于式(8)所描述的離散時間域系統，由于沒有確切的擾動值，故在MPC設計過程中不考慮擾動。基于式(8)，可計算輸出變量的N步長預測值為：

(9)

從式(9)可構建輸出預測矩陣Y(k)為：

Y(k)=Fx(k)+GU(k)

(10)

其中

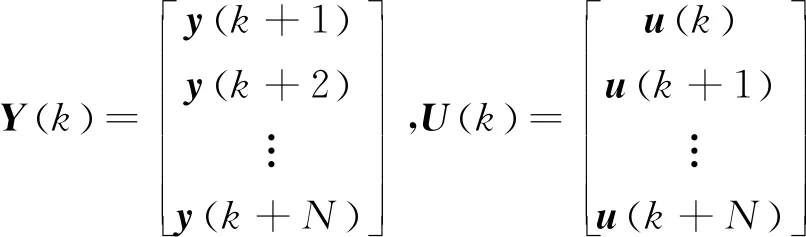
為了評估不同控制輸入作用下系統的性能，需定義與性能指標相關的成本函數表達式。當成本函數最小化時，則意味著系統在所期望的條件下運行。MPC中成本函數設計為：

(11)

式中，P和Q為已知的正定加權矩陣；w(k)為輸出參考值。利用下面的不等式，可使式(11)所描述的成本函數最小化：

[Y(k)-w(k)]TP[Y(k)-w(k)]+

UT(k)QU(k)<γ

(12)

式中，性能指標γ是正定函數，必須通過優化問題將其最小化[31]。由于式(12)中所包含的成本函數是非凸的，故需要將式(12)轉為凸結構。下面引出引理1。下文中，對于一個對稱矩陣M，采用“M>0”、“M<0”、“M≥0”和“M≤0”分別表示M為正定、負定、正半定和負半定。此外，diag{}代表對角矩陣。

引理1[32]：考慮一個仿射函數F′，其劃分為：

(13)

當且僅當滿足以下不等式之一時，有F′<0。

(14)

定理1：如果存在決策矩陣變量K(k)滿足以下具有線性矩陣不等式約束的凸優化問題，則將使成本函數式(12)最小化。

γ最小化，則有：

(15)

所獲得的控制信號不僅試圖將輸出變量保持在恒定值，并同時使性能指標γ最小。此外，還保證了輸出和控制信號的幅值在預設置區域內，該預設置區域由Umax、Umin、Ymax和Ymin定義。

證明：將式(10)代入式(12)，可得：

(16)

式(16)可重寫為如下形式：

(17)

通過使用引理1，將雙線性矩陣不等式(16)轉換為線性矩陣不等式條件，如下所示：

(18)

其中H11(k)為：

(19)

另外，對輸出信號和控制信號幅值的約束如下：

(20)

式中，Y(k)=Fx(k)+GU(k)。由于以上約束式是非凸的，為了將非凸條件轉換為凸條件，以對角矩陣的形式重新表示式(20)，從而式(20)轉換為線性矩陣不等式。至此，證明完成。

5 實驗驗證

為驗證所設計的直流微電網變換器MPC方案的性能，采用和文獻[24]中所描述傳統控制方案進行了對比測試，其中實驗平臺如圖5所示。圖5中直流微電網實驗平臺設有單個PPL，功率為2 kW，工作頻率為0.2 Hz，占空比為20%，即功率譜設置如圖6所示。

圖5 實驗平臺

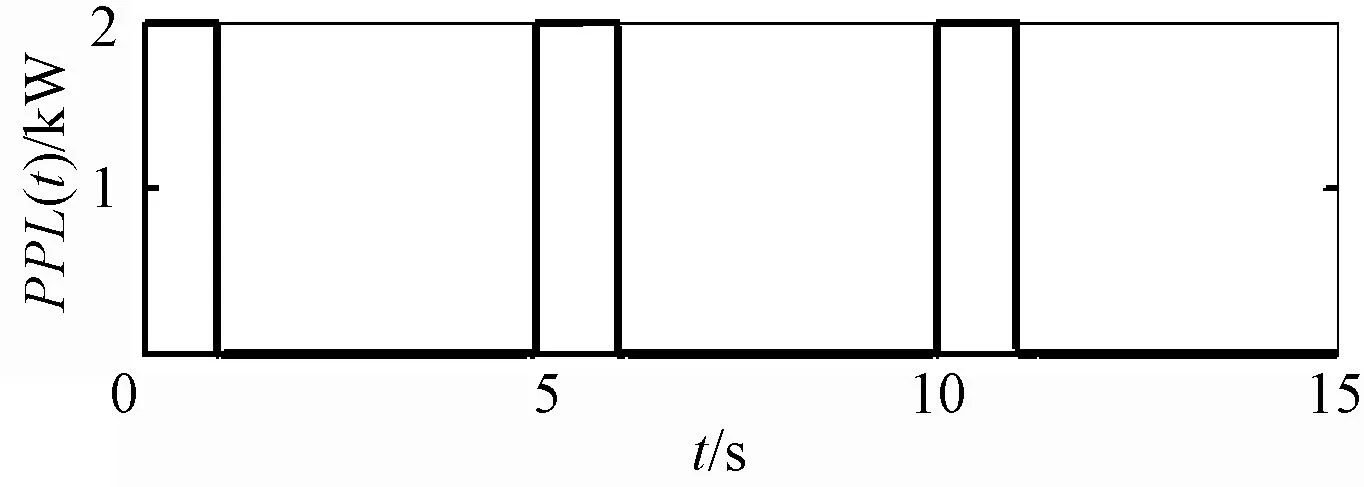
圖6 PPL功率譜設置

系統其他主要參數設置為：直流源動態模型中內電阻RMG和電感LMG分別為0.1 Ω和3 mH；超級電容CSC為0.1 F，其對應的Buck變換器中電感LSC為3 mH；電池組側雙向Buck-Boost變換器中電感LB和電容CB分別為3 mH和680 μF。除了系統參數外，工作點和輸出參考值設置為：

同時輸出信號設置的邊界為：

MPC算法中預測步長設置為N=4，采樣周期設置為T=1 ms。此外，在考慮狀態變量需滿足無量綱條件，以及不同輸出變量的權重后，設置成本函數式(12)中的加權矩陣P和Q如下：

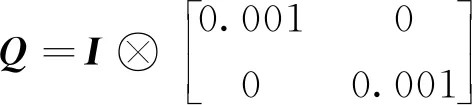
式中，“?”為Kronecker積；I為單位矩陣。通過應用定理1中的最優算法，可以計算每個采樣周期的狀態反饋控制增益矩陣。優化求解是基于Matlab平臺中的YALMIP工具箱實現的。進一步，基于Matlab/Simulink平臺構建控制律，并在dSPACE(DS1202)系統上生成可執行實時運行代碼，進而生成控制信號施加到Semikron變換器組件中。

如圖7所示為采用所設計的MPC方案下的直流微電網運行結果，同時還包含了傳統控制方案時的測試結果，以方便進行對比。其中直流微電網中的直流母線電壓uDC的波形如圖7(a)所示，從實驗結果中可以看出，傳統控制方案下，直流母線電壓較參考值相差更大，而MPC可有效補償PPL帶來的不利影響，使實際母線電壓較好地跟蹤參考值。圖7(b)為雙向Buck-Boost變換器電流iLB的波形，圖7(c)為超級電容CSC上電壓uSC的波形，超級電容分別在PPL工作和不工作期間放電和充電，相對于傳統控制方案，MPC方案下超級電容可盡快充電，故參考值跟蹤性能更好，這也可從圖7(d)為超級電容CSC充電電流iSC的波形看出，電流響應更快。圖7(e)為直流源輸出電流iMG的波形，可看出，傳統方案下，直流源須注入大電流以補償響應慢的問題，這意味著整流器上的電流過高，將提高整流器功率開關器件的電流應力要求。而所提出的MPC方案可保持整流器輸出電流在預定范圍內，對系統設計更為有利。

圖7 對比實驗結果

從圖7的實驗結果可觀察出，傳統控制方案和新型MPC方案都可以補償PPL的影響。新方案的優勢體現在系統瞬態響應明顯更快，可使超級電容盡快充電，并在穩態下，輸出變量快速收斂到所定義的參考值。而傳統方案下參考跟蹤的偏差較大，如表1所示為誤差信號的兩種范數在兩種控制方案下的對比關系，更清楚地反映出所提出的MPC方法相對于傳統控制方法的顯著改進。此外，MPC控制器可直接實現對直流微電網中Buck變換器和雙向Buck-Boost變換器的最優魯棒協調控制，而傳統方案則是對兩者分別進行控制的。

表1 誤差信號的兩種范數對比

6 結論

針對PPL對直流微電網的不利影響，本文提出了一種簡單有效的MPC作用于直流微電網中變換器的控制方法，從而實現了更穩定的系統協調控制。回顧全文，可歸納主要結論為：

(1)由于帶PPL的直流微電網系統存在一些系統約束，這使得標準線性控制技術無法使用，而MPC和線性矩陣不等式求解方法的結合，使得控制和輸出信號在嚴格約束下完成，最大程度地減輕PPL對系統的影響。

(2)和傳統控制策略的對比實驗結果表明，MPC直接作用于直流微電網中混合ESS，可使直流母線壓降優于傳統方案，同時動態響應更快。

進一步的研究方向是將該MPC方案推廣應用至其他配置更為復雜的直流微電網控制策略設計中。