Lévy 穩定過程均值變點監測在EWMA 和GLR控制圖中的比較

胡松瀛，李 泰

（亳州學院 電子與信息工程系，安徽 亳州 236800）

為優化自動系統的自動故障監測，工業生產中的質量控制等功能，就要解決在隨機系統中如何快速的監測出變點.為了快速監測出變點，就產生了不同的控制圖，例如：Shewhart［1］控制圖、EWMA［2］控制圖、CUSUM［3-4］控制圖、Cuscore［5-6］控制圖和GLR［7］控制圖.一些研究是基于隨機變量服從正態分布，或方差有限［8-9］.在實際問題中，大量的變量是服從穩定分布的，有無限方差，例如：年降雨量、刻畫核反應堆溫度的溫度分布、股票市場的收益率及金融網絡中的資金交易量，這些都是Lévy 穩定過程，可見研究Lévy 穩定過程均值變點具有十分重要的意義.在統計過程控制中，通過計算平均運行長度，考量控制圖監測均值變點的效果.筆者首先探討了控制圖EWMA、GLR 的平均運行長度的估計，其次分析了數字模擬比較.

1 預備知識

首先給出4 個定理［7］，利用這4 個定理得到其他定理.

依照規定，水行政執法機關一旦發現涉水違法行為可能觸犯刑法，有義務將相關案件移送至公安、檢察等司法機關處理。按照最高檢規定，水行政執法機關向公安機關移送案件，公安機關作立案、不立案決定處理，應向同級檢察院備案。但對未報送檢察機關備案的，沒有規定監督和懲罰措施，這使得部分水行政執法機關對應移送的案件持一種消極態度。雖然刑法第402條規定了行政執法機關不移送案件的刑事責任，但該條款的適用取決于檢察機關及時發現行政機關在移送案件過程中的瀆職行為。事實上在未及時備案又缺乏信息共享的前提下，檢察機關很難發現部分水行政執法機關的瀆職行為。

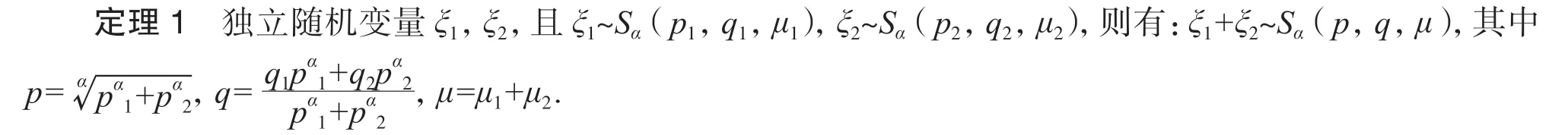
定理2 若ξ～Sα（p，q，μ），r是實常數，則：ξ+r～Sα（p，q，μ+r）.

定理3 隨機變量ξ～Sα（p，q，μ），k∈R，k≠0，有：

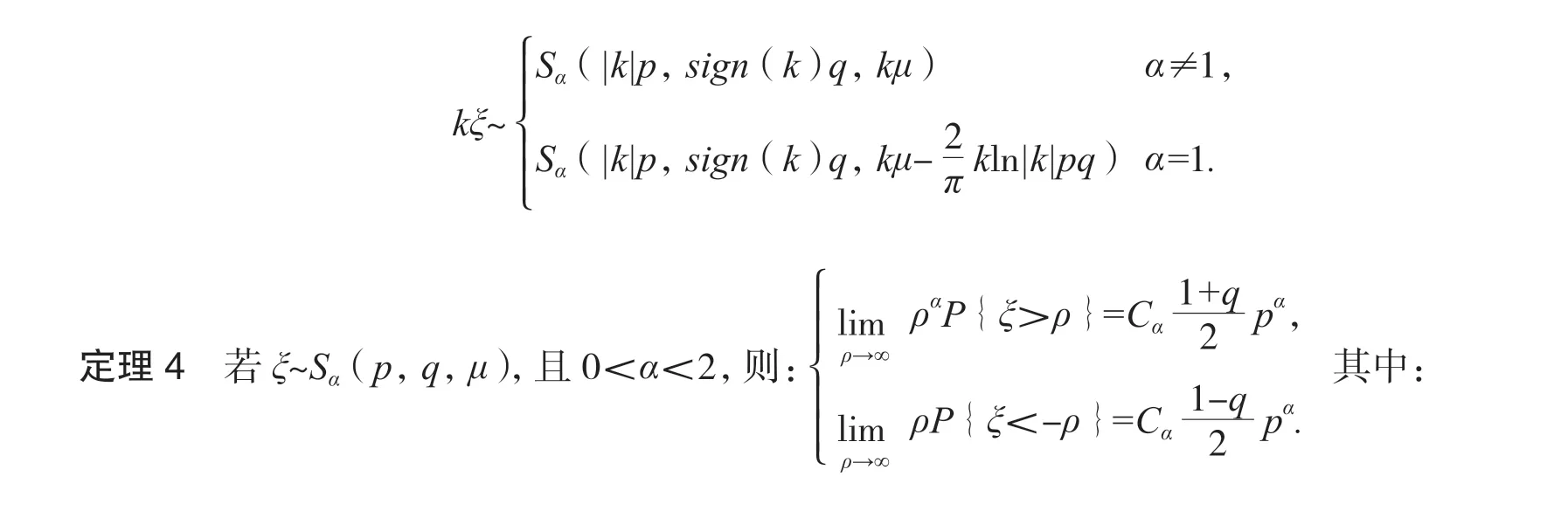
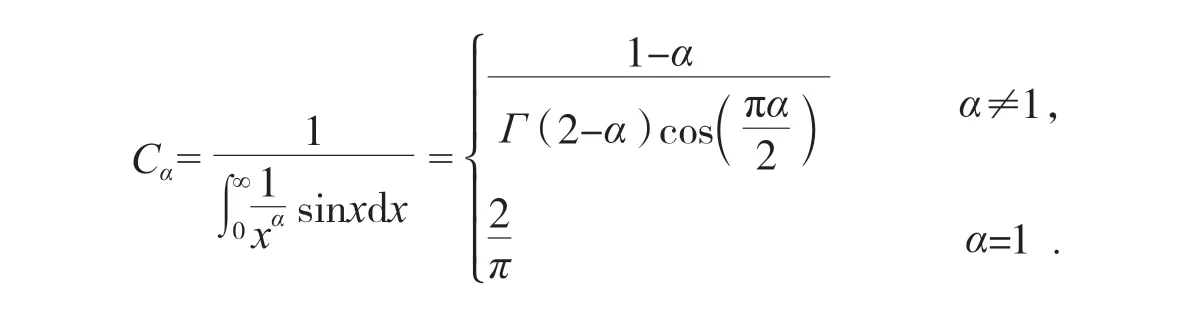
由此（2）式的向下不等式得證.下面證明（2）式的向上不等式.

定理6 設穩定過程的第i（i=1，2，…）個觀測值是ξi，ξi～Sα（1，0，μi）且相互獨立，1＜α≤2，μi≥0，令μ0=inf［μi］，μ0=sup［μi］，，對于EWMA 控制圖，有：

下面證明（3）式的向下不等式.

由于ξm（i=1，2，…）是相互獨立的一列隨機變量，根據定理4，有：

2 平均運行長度ARL 的估計

由于ξm（i=1，2，…）是相互獨立的一列隨機變量，根據定理4，有：

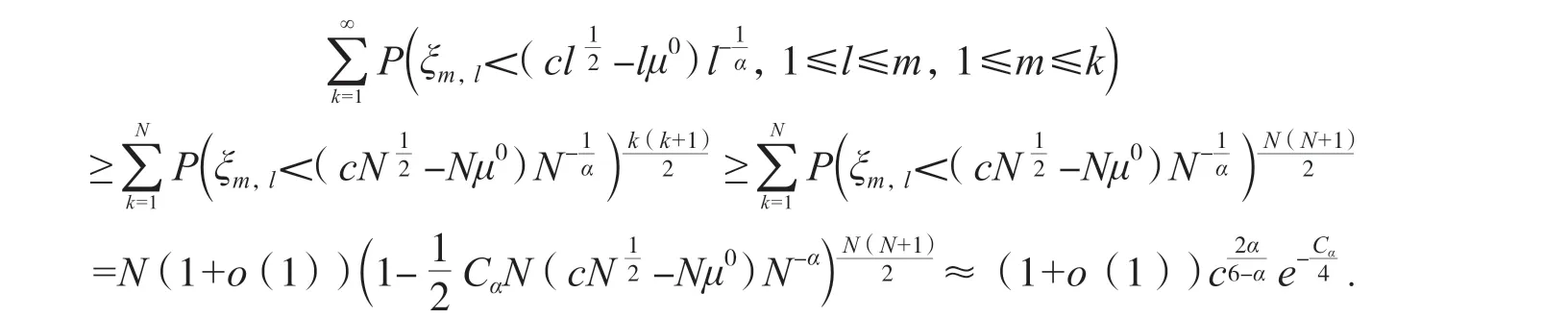
設ξi，i=1，2，…，n，是獨立穩定隨機變量序列，考慮檢驗問題：

定理5 證畢.

其中變點o未知，μ0≠μ，α∈（0，2］，q∈［-1，1］，p≥0.

目前，人工智能技術還處于初級階段。對于人工智能技術能達到何種水平，存在分歧。樂觀者，如人工智能科學家加里斯認為，人工智能的智力是人類的萬億個萬億倍(10的24次方)。在21世紀末，量子計算機的計算能力可能是當代計算機的萬億個萬億個萬億倍(10的36次方)。①這種人工智能可以稱為“超人”。屆時，人類與超人的智力差距，比細菌與人類的智力差距還大。但是，并非所有人工智能科學家都贊同加里斯的技術樂觀(不是社會效應樂觀)態度。

估計EWMA 和GLR 控制圖的平均運行長度之前，對一些符號先做出說明，沒有均值變化的概率和期望用P（·）和E（·）表示.ARL0表示受控平均運行長度，ARLμ表示失控平均運行長度，且：ARL0（T）=E（T），ARLμ（T）=Eμ（T）.其中T表示的是過程失控時的預警時間.考慮實際情況，c取充分大.

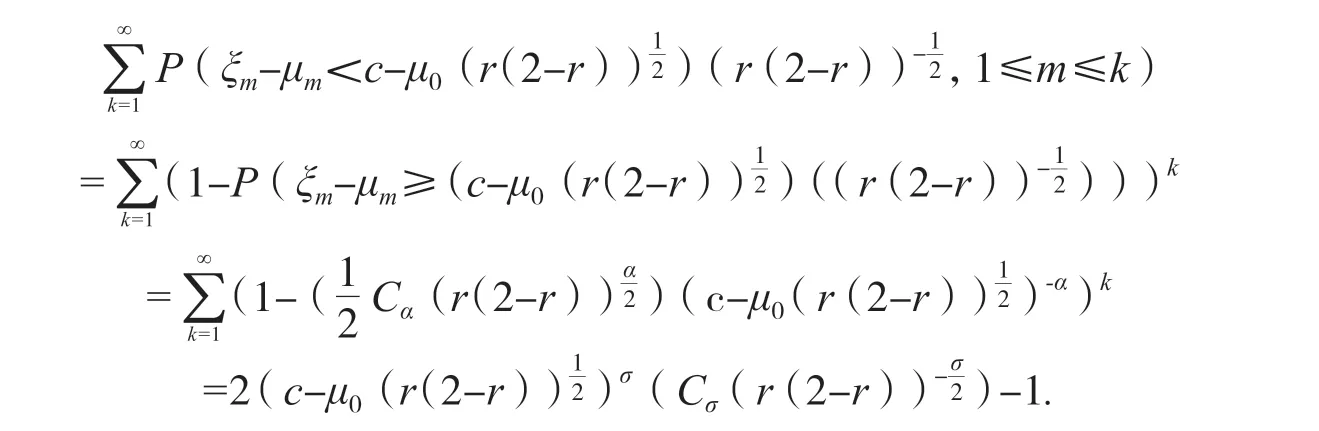
（3）式的向上不等式得證.

為了檢驗過程中均值有沒有變點，需要利用假設檢驗（1）式.假設在過程中變點沒有出現，那么接受H0；否則接受HA.在HA情況下，從時刻o開始，過程均值產生漂移μ-μ0.若μ＞μ0，就是向上漂移，若μ＜μ0，就是向下漂移.不論是雙向飄移，還是向下漂移，它們的監測與上漂移的監測沒有本質區別，筆者僅就向上漂移的監測作出探討.

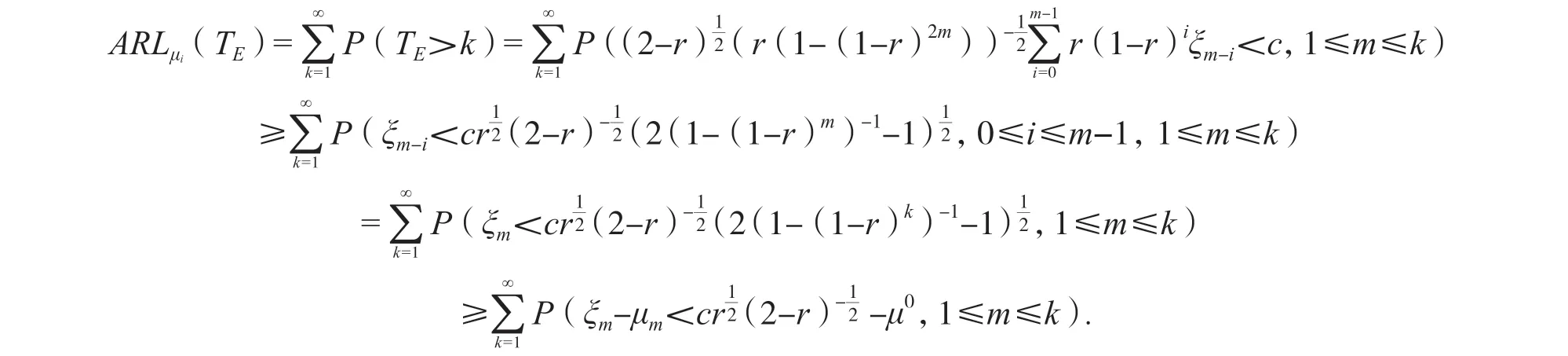
MONARCH-2[11]是一項Ⅲ期、雙盲臨床研究，入組了669例HR＋和HER2-的晚期乳腺癌患者，按2∶1的比例隨機分為接受abemaciclib（150 mg，2次/d，持續給藥）或安慰劑聯合氟維司群治療組。結果顯示，abemaciclib組和安慰劑組的mPFS分別為16.4個月和9.3個月（HR＝0.553，95% CI：0.449～ 0.681，P＜ 0.001）。

從孔子“禮”的發生機制來看，禮必須具有能指導主體實踐的功能。前文提到，孔子之“禮”是在周禮實踐基礎上之改造再實踐。禮的核心內容包含了對人倫關系的規定。孔子強調，仁是禮的核心內涵，所以禮的內容主要著眼于仁的約制規范和實踐。孔子主要從以下兩個方面進行對于禮的規制的：其一是處于特殊的身份、地位的道德實踐主體擁有不同的道德實踐義務與原則，其一是作為一般普遍意義上而言的道德實踐主體又必須必須具有共同的行為準則。

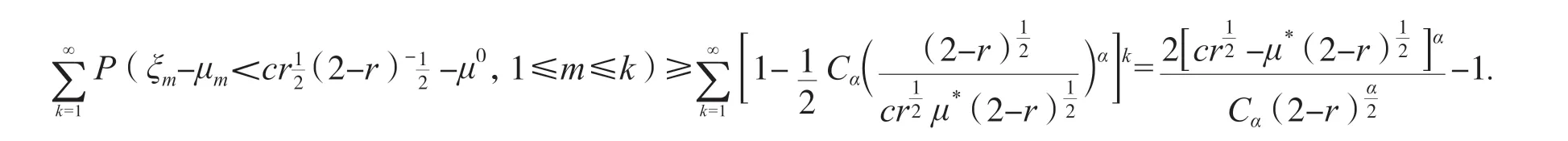
定理6 證畢.

3 數字模擬

檢驗控制圖效果的一個標準是平均運行長度ARL0，在受控的前提下，并且ARL0以及均值漂移μ相等，需要比較失控狀態時的平均運行長度ARLμ，ARLμ小的控制圖的效果就是較優的.這里僅就σi=1.5 和σi=1.8 時，比較EWMA 和GLR 這兩種控制圖的平均運行長度ARLμ.表1 和表2 給出了EWMA 和GLR 這兩種控制圖在Xi～S1.5（1，0，μ）和Xi～S1.8（1，0，μ）狀態下的平均運行長度.模擬的結果是由多次重復試驗獲得，其中隨機變量序列Xi～Sαi（1，0，μ）是由rstalbe 程序生成的.

第一，構建了完備的法律體系。美國早在1965年起，為了能夠為老年人的醫療、救助、安養機構提供法律保障，出臺了《多目標老人中心方案》、《老年法》等法律。其次，建立完善的養老金制度。由于美國強大的養老金制度的支持，使得市場力量能夠大量引入美國養老機構中。

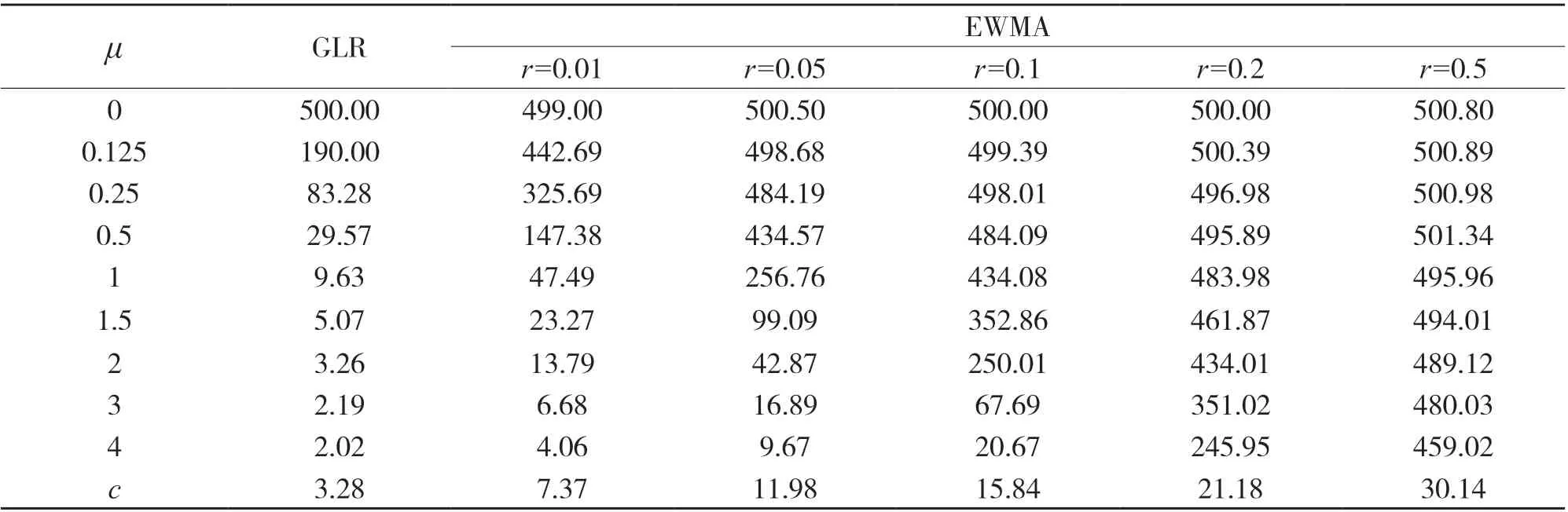
表1 Xi～S1.5（1，0，μ）情況下兩種控制圖平均運行長度的比較

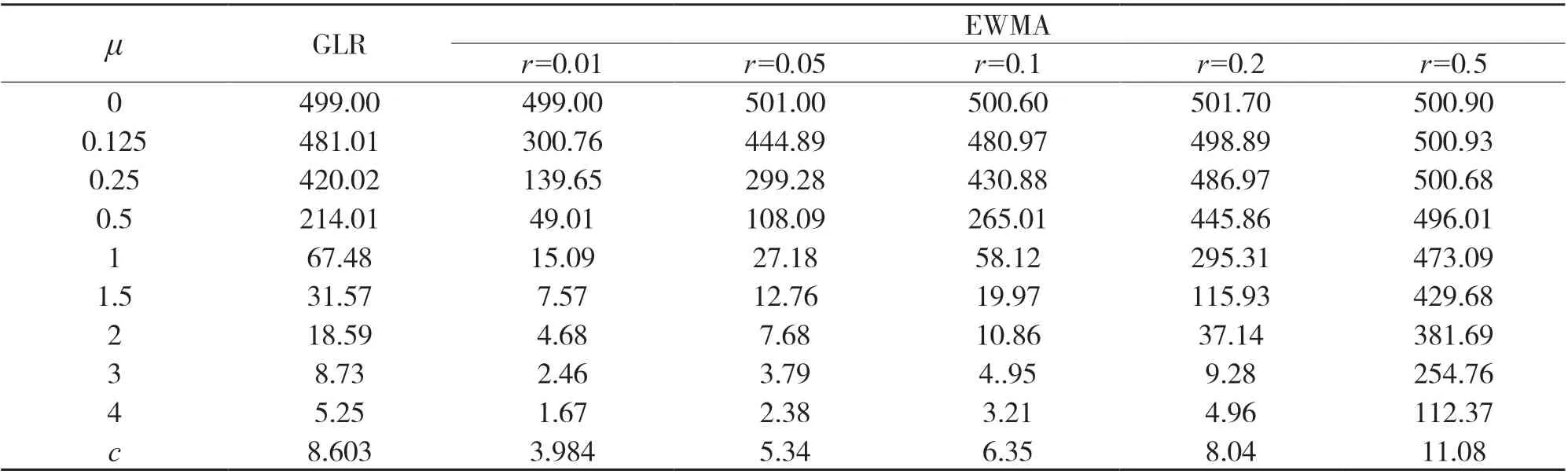
表2 Xi～S1.8（1，0，μ）情況下兩種控制圖平均運行長度的比較

4 分析數據

從表1 可以看出，在α=1.5 穩定分布中，GLR 的效果明顯比EWMA 的好.從表2 可以看出，在α=1.8穩定分布中，當r＜0.1 時，EWMA 的效果明顯比GLR 的好；r=0.1 兩者的效果相差不大，隨著r的增大，EWMA 的效果不如GLR 的效果.