基于布谷鳥搜索優化馬爾可夫的文件熱度預測

王 彪,王克儉+，何振學，高萬豪，魏雪川

(1.河北農業大學 信息科學與技術學院，河北 保定 071001；2.天津城建大學 控制與機械工程學院，天津 300384；3.國網河北省電力公司 石家莊供電公司，河北 石家莊 050052)

0 引 言

云計算平臺搭建在大規模服務器之上，通過系統中存儲的大量數據提取有價值的信息[1]。在對分布式文件系統的研究中，如何有效提高系統的可靠性和訪問效率成為當今的研究熱點[2]。現有分布式文件系統副本管理機制分為靜態管理和動態管理[3]。靜態管理因副本數目固定，難以確保高熱度文件的訪問效率[4]。動態管理根據資源環境的動態變化動態調整副本的數目，可提升文件訪問效率和存儲空間利用率[5]。

文獻[6]針對靜態副本策略的缺點，提出基于灰色模型的預測模型，根據文件最近的訪問特征預測數據未來訪問熱度。文獻[7,8]依據時間局部性原理，最近訪問的文件短時間內會被再次訪問。文獻[9,10]采用組合預測模型應對單一預測模型的局限性。文獻[11]神經網絡模型在建立過程中需要設置準確的層次和大量的樣本空間進行訓練，文件熱度預測效率低。文獻[12]采用了灰色馬爾可夫模型，利用C均值聚類法分析儀器設備信號數據頻譜輪廓峰值幅值序列殘差狀態，對殘差預測值進行修正，但效果不是很好。

綜上，目前已有的文件熱度預測方法都存在一些缺點，本文采用布谷鳥搜索(cuckoo search，CS)優化的馬爾可夫模型修正無偏灰色預測文件熱度，消除灰色預測的固有偏差，提高預測精度。此方法首先采集文件歷史訪問熱度，通過優化算法利用新陳代謝思想，對文件熱度序列進行預測更新，利用最新的熱度數據對未來熱度進行預測。

1 CS無偏灰色馬爾可夫模型理論

1.1 灰色預測模型

灰色模型主要用于具有不確定因素的灰色系統進行預測。其優點是可以利用少量不完整信息，通過建立數學模型并對數據未來的發展趨勢做出預測的一種模型。灰色預測模型定義請參見文獻[13]。本文采用灰色預測模型應用于文件熱度預測，將文件歷史訪問熱度作為預測數據序列，通過對預測序列進行簡單變換，從中尋找數據變動規律并對文件未來的熱度發展趨勢進行預測。

1.2 馬爾可夫模型

馬爾可夫模型根據在不同狀態之間轉移的概率對未來的發展趨勢進行預測。系統在狀態轉換過程中第n次轉換后的狀態決定于前一次(第n-1次)結果狀態。馬科夫模型定義請參見文獻[14]。本文關于文件熱度預測，因用戶訪問的隨機性和數據熱度變化的突發性是兩個不可避免的因素，導致灰色預測可能會產生較大的誤差，故采用馬爾可夫模型預測未來一段時間內文件訪問量所在的狀態區間，對文件熱度預測偏差進行修正，提升模型預測準確性。

1.3 布谷鳥搜索算法

布谷鳥搜索(CS)算法最早由楊新社和S.戴布提出，是一種自然啟發式算法。具有收斂速度快、效率高、調節參數少等優點[15,16]。該方法基于布谷鳥的寄生性育雛和Lévy飛行。

這個算法的靈感來自布谷鳥的寄生繁殖行為。在自然界中，布谷鳥在寄主鳥的巢中產卵，被識破后破壞或干脆放棄巢。為了降低蛋被破壞或遺棄的可能性，一些布谷鳥模仿寄主鳥蛋的顏色和圖案；一些布谷鳥選擇合適的時間孵化蛋，通常比寄主鳥早，拿走一些寄主鳥的蛋，以增加后代獲得更多食物的機會。尋巢過程可以看作Lévy飛行，一個Lévy飛行是一種隨機行走。

該算法的實現將所有的寄主巢看作是一代，每個巢穴都攜帶鳥蛋作為解決方案。目標就是通過不斷地迭代尋找潛在的最優解來取代現有的方案。本文用到的是對多目標優化的布谷鳥搜索算法。基于以下3個準則：

(1)每只布谷鳥一次產下k枚蛋(代表k個目標的解決方案)，將它們放在隨機選擇的某個寄主巢穴中；

(2)每一代中有高質量蛋(解決方案)的最佳巢穴被帶到下一代；

(3)可用的寄主巢數量是固定的，寄主發現布谷鳥放的蛋概率為pa∈(0,1)。 發現后，寄主可以消滅該蛋或放棄舊巢另建新巢。

本文運用CS搜索算法對馬爾可夫狀態區間與實際值和預測值之間的關系進行發掘，尋找該區間最合適的值對預測值進行修正。

2 CS動態無偏灰色馬爾可夫模型建模

灰色馬爾可夫模型在針對小樣本和指數分布樣本數據預測方面應用廣泛，但是該模型仍然存在不足。本章主要從灰色模型參數、馬爾可夫修正值計算、預測數據序列更新3個方面對該模型進行優化并對該模型進行建模。

2.1 無偏灰色預測

本文利用無偏灰色預測模型對文件訪問量序列進行處理并預測未來文件熱度。該模型通過對灰色發展系數a和灰作用量u的優化，解決了灰色預測固有偏差，達到減小預測誤差的目的。借助灰色模型的灰色發展系數a和灰作用量u確定無偏灰色預測模型的原始數據序列擬合模型，對文件未來熱度進行預測。

無偏灰色模型的原始數據序列為某文件在前m個相等時間段內的文件訪問量。建模過程如下：

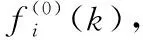
(2)對該文件歷史訪問量序列進行累加處理：累加序列的首個數據直接獲取原始序列的第一個數據，從第二個數據開始將原始序列的第n個數據與第n+1個數據相加作為新序列的第n個數據。根據式(1)得到累加序列

(1)

(3)準指數檢驗與光滑性檢驗

準指數檢驗，級比表示見式(2)

(2)

光滑性檢驗，時間序列光滑比表示見式(3)

(3)

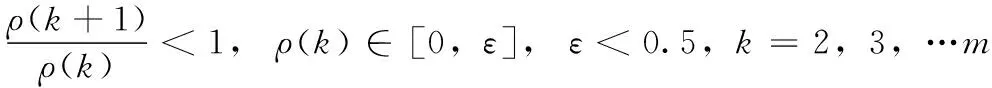
(4)累加序列的變化趨勢我們可以近似使用式(4)白化微分方程來描述

(4)

該微分方程中參數a和u為待識別常量，其中a稱為發展系數，u為灰作用量。

(5)模型求解：采用最小二乘法求待識別常量的估計值。

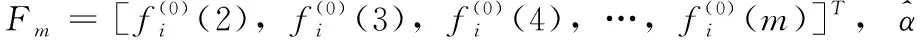
(5)

模型表示見式(6)

(6)

(6)求解白化微分方程，得到無偏灰色預測的離散時間響應函數，見式(7)

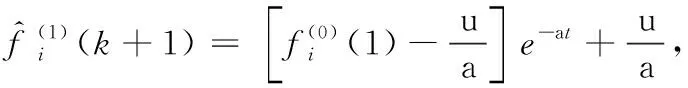
(7)

(7)基于灰色模型中參數估計值a、u得到無偏灰色預測模型中的參數b、A，消除固有偏差，見式(8)

(8)

(8)無偏灰色預測模型的原始數據的擬合模型見式(9)

(9)

通過對灰色預測模型參數的更新，無偏灰色預測模型無需在進行預測數據累減還原，簡化了建模步驟同時還提升了系統的運算效率。

2.2 CS優化的馬爾可夫對預測值修正

在馬爾可夫模型中，選取灰色預測值所處狀態區間的中心值對其進行誤差修正。但僅考慮狀態區間的中心值可能會忽略其它誤差分布信息的影響，狀態區間的中心值并不能適當代表誤差狀態。因此，為馬爾可夫模型對灰色預測值進行更加準確地修正，本文借助布谷鳥搜索算法更深入地挖掘狀態區間信息，以識別更具代表性的修正值，而不是狀態區間的中心值。CS優化馬爾可夫模型具體建模過程如下。

2.2.1 馬爾可夫模型

馬爾可夫模型見式(10)所示

X(m)=X(t)P(m-t),t=1,2,3,…,m-1

(10)

其中，狀態X(m)為初始狀態概率向量X(t)經過(m-t)個時刻之后的狀態概率向量，向量P為一步狀態轉移概率矩陣。

2.2.2 狀態區間劃分

本文由相對精度來確定狀態區間的劃分，相對精度為實際值和預測值差值，即殘差。每個數據根據自己的相對精度區分所處狀態。為了適應不同數據序列預測，首尾狀態的區間的邊界值選取相對精度的最值。狀態個數一般取3個～5個，將目標區間等分。

2.2.3 狀態轉移概率矩陣構造

這里采用頻率近似等于概率的思想，利用式(11)計算狀態轉移概率

(11)

假設劃分了n個狀態區間，nij(k) 表示熱度預測值所在狀態區間Ei經k步轉移到狀態區間Ej的次數，ni為所在狀態區間Ei的數據個數。按照上述方法計算即可得到k步狀態轉移概率矩陣，如式(12)所示

(12)

2.2.4 CS優化馬爾可夫修正值

假設狀態區間i為 [ai,bi]， 經布谷鳥搜索算法優化后的修正值計算見式(13)

vi=αiai+(1-αi)bi,i=1,2,…,n

(13)

本小節優化的目標就是對每個狀態區間尋找合適的馬爾可夫修正值，前提就是尋找到每個區間的參數α。當α=0.5時，修正值就是狀態區間中心值。下文介紹布谷鳥搜索算法尋找狀態區間決策系數α=(α1,α2,…,αn)。

(1)布谷鳥搜索區間決策系數

CS搜索方式是基于Lévy飛行的直接搜索和基于宿主鳥在巢中發現外來蛋的概率的隨機搜索。

如下方法實現局部隨機搜索，計算方式見式(14)

(14)

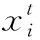
本文借助Lévy飛行實現全局隨機搜索，由于方向的選擇是隨機的，各方向的概率都是一樣的，服從均勻分布。還要確定需要搜索范圍，Lévy分布要求大概率落在值比較小的地方，于是借助Mantegna算法可以近似滿足這樣的情況，具體建模過程見式(15)、式(16)、式(17)

(15)

(16)

(17)

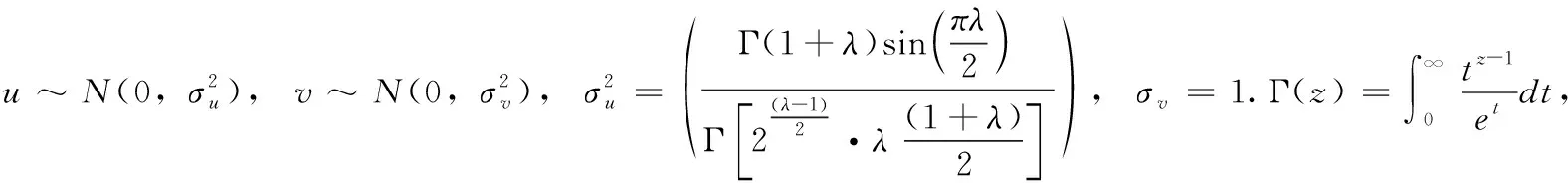
(2)迭代過程中最優方案判定

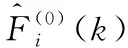
(18)

(3)修正值計算

由第一步搜索出的最優決策區間系數α=(α1,α2,…,αn)， 計算每個狀態區間的修正值。根據式(13)，得到修正值v1,v2,…,vn

(19)

2.2.5 馬爾可夫對預測值修正

通過k步狀態轉移概率矩陣和當前數據所處狀態Ei及其初始向量X(0)， 可以對下一時刻預測值所處狀態進行預測。假設max(Pij)=Pik， 則認為下一時刻數據最有可能由狀態Ei轉向Ek。

本文根據相對精度劃分每個狀態區間，根據此相對精度來對無偏灰色預測對預測值進行修正，減小誤差，增加預測的準確度，如式(20)所示

(20)

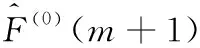
2.3 數據更新

數據更新是對灰色預測模型的預測序列進行優化。本文采用的是基于灰色預測模型對文件熱度進行預測，該模型特點就是針對小樣本對數據預測。數據訪問有時間局部性特征，當前被頻繁訪問的文件在未來的一定段時間內存在較高的概率會被再次訪問，因此較舊的數據不能很好地反映當前的趨勢變化。

分布式系統中的文件每時每刻都在被訪問，隨時會產生最新的文件訪問量數據。為了能夠更加準確地利用歷史熱度對未來的文件熱度進行預測，根據文獻[8]新數據權重高的思想，采用新陳代謝思想對原始數據序列進行等維處理。更新數據序列時，將最新的文件熱度加入原始序列中，剔除陳舊的熱度數據，如式(21)。根據文件統計周期循環以上操作，即可更新文件熱度預測序列。這樣能更好地反映文件最近熱度的變化趨勢，更準確地預測文件未來熱度

(21)

3 實驗與結果分析

3.1 原始數據及預處理

為達到真實模擬用戶對文件訪問量的變化，本文數據來源于某社交通訊軟件實時數據，如表1所示。表中數據是每隔10 min收集一次用戶對某文件的訪問量(文件熱度)，以此作為處理前的原始數據序列。以此數據序列來驗證幾種預測模型的擬合效果，做出分析比對。

表1 某社交通訊平臺用戶對熱點新聞實時訪問量

首先對原數列進行累加得到新的數列，對新數列進行光滑和指數規律檢測。通過式(2)、式(3)以及檢驗標準，驗證該累加序列為光滑序列，并且具有指數規律，可以采用灰色模型對未來數據進行預測。

3.2 實驗設置及實驗評價

3.2.1 實驗參數設置

經過多次實驗對CS算法的參數進行調整，最終確定綜合考慮算法效率和準確度對參數進行了設定。見表2。

表2 CS算法各項參數設置

3.2.2 實驗相關評價

本文對預測模型的擬合程度評價指標為相對誤差絕對值的平均值(MAPE)，如式(18)所示。根據MAPE既可以判定模型預測效果是否良好，又可以作為模型之間效果比較的參考。

3.3 實驗過程及實驗結果分析

3.3.1 狀態區間劃分

根據灰色模型和馬爾可夫模型基本原理，代碼實現相關功能，并對數據進行了處理。實現了幾種模型依據原始數據序列對未來文件訪問量的預測。其中灰色預測模型發展系數a=0.0061，灰作用量u=385.1279。無偏灰色預測模型參數b=-0.0061，A=383.9498。根據各模型對原始數據序列的預測擬合結果，通過計算殘差我們取殘差的兩個最值作為狀態區間的邊界，并將其等分為3個區間，對應E1，E2，E3這3個狀態。此處的狀態個數與CS算法參數宿巢容量數值相同。如表3、表4分別給出了狀態區間的具體劃分和無偏灰色馬爾可夫模型的殘差。

表3 馬爾可夫修正狀態區間劃分

表4 無偏灰色模型預測值與實際值的殘差和具體狀態

根據表4數據顯示每個數據所處狀態，在這里給出一步狀態轉移概率矩陣。狀態轉移概率矩陣用于對未來訪問量的預測，以提前應對文件訪問量突增，及時對文件副本進行動態調整

3.3.2 馬爾可夫修正值

默認的馬爾可夫修正值為區間中值，狀態區間的中心值并不能適當代表誤差狀態。借助布谷鳥搜索算法更深入地挖掘狀態區間信息，以識別更具代表性的修正值。經過布谷鳥算法優化的修正值由式(19)計算。

通過CS算法迭代尋優，當迭代次數為100次的時候已經可以顯示出預期效果。綜合考慮實驗準確性和計算效率，本文將迭代200次，得到α=(α1,α2,α3)=(0.9883,0.4183,0.4889)， 得到優化馬爾可夫修正值。v=(-84.81，-4.56,42.93)。 這里有一點需要注意的是得到的馬爾可夫修正值僅適合該預測序列的預測值殘差修正。當預測序列經過新陳代謝思想更新后，還需要再次預測α最優解，才能達到優化預測殘差的最優效果。

3.3.3 CS優化的無偏灰色預測模型分析

表5展示了本文預測修正模型與默認情況下的擬合效果對比，以此評判該預測模型的優化效果。殘差由實際值減去擬合值得到。相對殘差為殘差絕對值與實際值的比值，最后采用MAPE對3種模型擬合度進行評測。

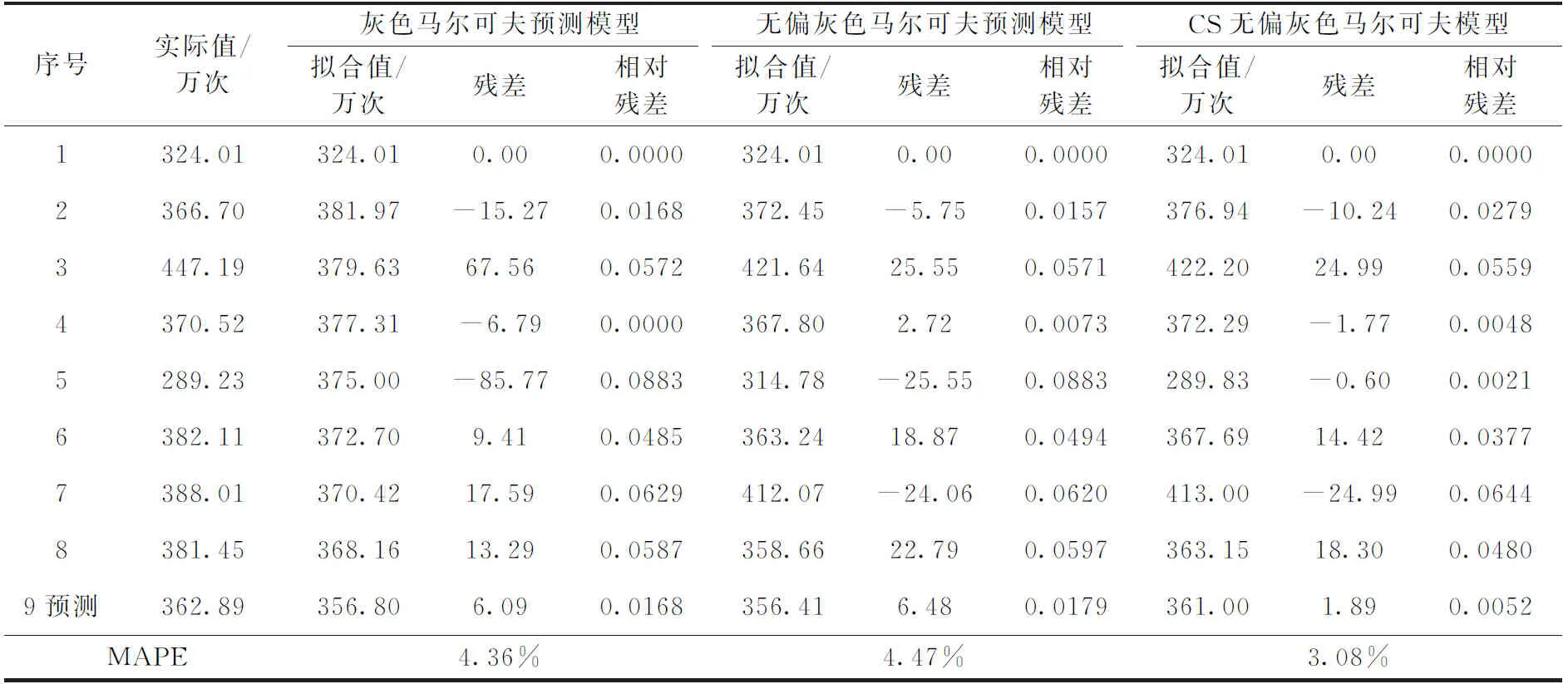
表5 3種灰色預測模型修正后擬合效果對比

如圖1所示，給出了灰色模型(grey model)、無偏灰色模型(unbiased grey model)、灰色馬爾可夫模型(grey Markov)、無偏灰色馬爾可夫模型(unbiased grey Markov)、CS無偏灰色馬爾可夫模型(CS unbiased grey Markov)與實際值之間的擬合效果。其中1個～8個周期是擬合值，第9個周期是預測值。

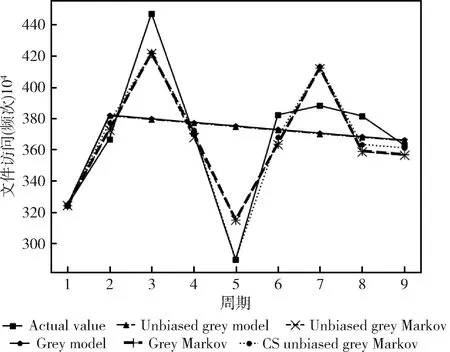
圖1 5種灰色模型擬合效果對比

實驗結果表明，灰色馬爾可夫模型和無偏灰色馬爾可夫模型的MAPE都在4.4%左右，說明馬爾可夫修正模型對縮小灰色模型的誤差有很好的效果。而經過CS算法優化后的馬爾可夫模型對誤差的修正又有所提升，MAPE僅為3.08%。

為了進一步說明CS無偏灰色馬爾可夫模型在小樣本預測情景下，能夠有效的對下一時刻數據進行快速、準確的實時預測。我們采用同一組的數據進行實驗，對未來的幾個時刻訪問量進行預測，將其與BP神經網絡和文獻[17]中灰色神經網絡模型進行對比，以MAPE作評價指標。

實驗將本文方法與幾種常見預測方法通過預測值的MAPE進行比較，預測值擬合程度如表6所示。得出結論：灰色模型和無偏灰色模型在預測準確性方面幾乎相同，但是無偏灰色預測模型預測結果就是預測值，無需進行累減操作，計算效率會略高。CS無偏灰色馬爾可夫模型在小樣本的情景下，MAPE要小于其它模型，比其它幾種模型MAPE平均值降低了2.26%。對數據預測準確度更高。說明該模型可以更好地利用少量數據預測短期內未來時刻的數據變化，對提前應對未來環境變化，采取相應措施提供有力依據。

表6 幾種模型的預測結果擬合度匯總/%

4 結束語

本文采用CS優化的馬爾可夫模型修正無偏灰色模型預測值，采用新陳代謝思想更新數據，使預測序列保持最新文件熱度值，對預測文件下一時刻熱度起到重要作用。馬爾可夫模型修正可以有效降低灰色預測模型因數據波動而產生的誤差，提高了預測數據的準確度，經過CS優化的馬爾可夫模型可以更好縮小誤差值。通過與幾種預測模型對比，CS優化的灰色馬爾可夫模型平均相對殘差最小，說明該模型在數據量少的情況下，能夠對文件熱度預測達到較好效果。接下來的研究會根據文件熱度進行副本個數的調整，降低熱點文件訪問沖突和執行時間，提升系統效率和資源利用率。