基于分數階混合蝙蝠算法的Otsu圖像分割
梁遠哲,馬 瑜,江 妍,王 原,馬 鼎,李 霞
(寧夏大學 物理與電子電氣工程學院,寧夏 銀川 750021)
0 引 言
圖像分割是計算機視覺的重要組成部分,其主要目的是從圖像中分離出需要的目標區域,其中基于閾值的圖像分割應用廣泛。最大類間方差法(Otsu)是一種閾值分割方法,根據灰度特性將圖像分為兩部分,類間方差最大值為閾值[1]。二維Otsu算法相較Otsu算法有著更好的分割效果[2]與抗噪性能[3]。申鉉京等[4]提出了一種基于時間復雜度的多閾值Otsu快速分割算法,提升了算法的計算效率,能夠較好地應用于實時環境。
蝙蝠算法(bat algorithm,BA)是受蝙蝠覓食行為的啟發而提出的一種新型群體智能算法[5],近年來受到廣泛應用。裴宇航等[6]提出一種動態調整慣性權重的自適應蝙蝠算法,提升了尋優性能。Vallikutti Sathananthavathi等[7]將蝙蝠算法應用于視網膜血管圖像分割,對于血管的識別具有很高的靈敏度。
分數階微積分作為一種數學模型近年來得到了廣泛的應用。魏晶茹等[8]將分數階微積分與粒子群算法結合來進行圖像分割,提升了分割效果。Yashar Mousavi等[9]在螢火蟲算法中引入分數階來處理混沌系統的參數估計問題,取得了可觀的實驗結果。
針對蝙蝠算法在圖像分割中尋優精度與收斂速度的問題,本文將分數階微積分引入蝙蝠算法中的速度更新階段,提高其搜索能力。在蝙蝠算法的全局尋優階段引入天牛須搜索算法(beetle antennae search,BAS)[10]以加快蝙蝠算法的收斂速度并結合二維Otsu算法獲取最佳分割閾值,提升了圖像分割精度與收斂速度。
1 二維Otsu閾值分割算法
日本學者大津在1979年提出了一種自適應閾值分割算法,即為Otsu算法。其主要原理是通過圖像的灰度特性將圖像分成目標與背景兩類,首先統計出在整幅圖像里灰度級中每個像素的個數,計算圖像中所有像素點的概率分布,對于每一個灰度級,計算出該灰度級下目標與背景的類間概率,通過目標函數計算出目標與背景的類間方差,類間方差越大說明構成圖像兩部分的區別越大,因此類間方差越大則圖像分割效果越明顯。
二維Otsu算法是在Otsu算法的基礎上提出的,相較于Otsu算法,二維Otsu算法同時考慮到了像素灰度級分布和它們的灰度級與鄰域像素平均灰度級之差的分布,因此得到的閾值是一個二維矢量灰度-梯度。若將橫坐標視為灰度,縱坐標視為梯度,則形成了圖像的灰度-梯度二維直方圖。此時,概率集中分布在梯度值較小的區域,此區域為圖像的背景與目標區域,而圖像的噪聲、邊緣區域分布在梯度值相對較大的區域,這樣就實現了圖像目標與背景的分離,減少了噪聲信息的干擾。
假設一幅大小為M×N的圖像,其灰度為i,梯度為j的像素nij出現的概率是
(1)
若分割圖像的閾值平均灰度為s,梯度為t,則閾值(s,t)將灰度圖像分成兩類,用B表示背景類、T表示目標類。它們兩者的概率分布可表示為
(2)
其中,L表示圖像的灰度級數。用μB和μT表示背景類、目標類的均值向量,μ表示所有像素的總均值向量,它們可表示為
(3)
(4)
(5)
離散度測度函數表示為
S(s,t)=PB×(μB-μ)×(μB-μ)T+
PT×(μT-μ)×(μT-μ)T
(6)
離散度測度的值代表目標與背景兩類之間的差別,越大則目標與背景兩類的差別越大,圖像分割效果越好。所以使離散度測度函數的值最大時的自變量(s*,t*)就是圖像的最佳分割閾值,表示為
tr(S(s*,t*))=Max(tr(S(s,t)))
(7)
2 分數階混合蝙蝠算法
2.1 傳統蝙蝠算法與其缺陷分析
蝙蝠算法啟發于蝙蝠覓食時的回聲定位能力。蝙蝠算法模擬自然界中蝙蝠利用超聲波對獵物進行判斷與定位,從而逼近、捕獲獵物。參考文獻[6]可知因為蝙蝠算法僅含有頻率、速度、位置等參數,所以相較于其它優化算法結構較為簡潔,在有效性與準確性方面也有著優勢。如今蝙蝠算法在各個領域中都有著廣泛的應用。
在蝙蝠算法中,蝙蝠通過以下3個理想化的規則來進行獵物捕獲。
所有蝙蝠都通過回聲定位法感知距離,并且蝙蝠能夠判斷出是否遇到所需的獵物。
每一只蝙蝠在位置x處以速度v隨機飛行,通過可變頻率f、固定波長λ、脈沖發射率R、音量A來尋找目標獵物。蝙蝠通過自身與獵物的接近程度自動調節其發射頻率與脈沖發射率。
雖然有多種音量變換方式,但是在算法中假設音量均為正數,其范圍屬于[Amin,Amax]。
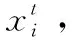
fi=fmin+(fmax-fmin)β
(8)
(9)
(10)
式中:β∈[0,1]為服從均勻分布的隨機變量,x*為當前找到的最優解。
當尋找出一個最優解時,開始局部搜索階段,通過下式產生新的解
(11)
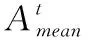
蝙蝠的脈沖發射率與音量的更新公式為
(12)
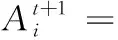
(13)
其中,常數γ>0,0<ξ<1。
雖然相較于其它群體智能算法,蝙蝠算法有著參數少,較為靈活和簡單等優點,但仍存在一些缺陷。經過分析主要有以下兩點問題:
(1)從蝙蝠通過回聲定位來追尋獵物的機理和蝙蝠個體的更新方式可看出,蝙蝠算法中蝙蝠個體的探索能力很大程度上取決于速度,通過速度改變當前蝙蝠的位置進而影響到算法整體的優化效果。而傳統蝙蝠算法的速度忽略了歷史速度的狀態,缺乏對歷史的繼承,這導致算法的全局搜索過程不夠均衡,更新后的蝙蝠個體很容易被局部值吸引而陷入局部最優。
(2)傳統蝙蝠算法在局部搜索階段過于依賴隨機選擇與概率分布來生成新的蝙蝠位置,隨機性會導致種群的多樣性受到影響,最后導致算法在后期最優值附近花費較多的時間。
2.2 分數階微積分
分數階微積分是傳統微分與積分的推廣[11],對歷史具有記憶性,能夠改善整數階微積分只與當前狀態有關的局限性[12]。近年來分數階微積分在信號處理、圖像處理、控制工程等領域得到了廣泛的應用。分數階微積分有多種定義,常用的G-L(Grumwald-Letniko)定義表達式為[13]
(14)
其離散表達式為[13]
(15)

2.3 天牛須搜索
天牛須搜索(beetle antennae search,BAS)是在2017年提出的一種新型仿生算法,具有很強的全局搜索能力。其原理為,天牛在覓食過程中通過左右兩個觸須感應到的氣味強度來判斷食物的大致方位,若右邊觸須感應到的氣味較強時則向右移動,反之則向左移動,移動一段距離后再次使用兩個觸須感應氣味,直到移動到氣味最濃的位置即找到最優解[14]。
天牛須搜索的數學描述為[14]:
(1)對于目標函數為f的n維優化問題,設天牛位置為S,左觸須Sl,右觸須Sr,左右觸須相隔d,步長為
step=c*d
(16)
在空間中天牛的朝向隨機,因此左右觸須的方向可用n維隨機向量表示為
dir=rand(n,1)
(17)
(2)此時得到兩個觸須的位置
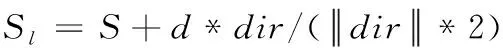
(18)
求出兩個觸須的適應度fl和fr,比較兩者大小,天牛向適應度大的方向移動,移動后的位置為
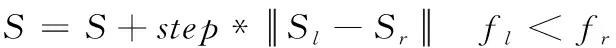
(19)
(3)求出天牛新位置的適應度fs,更新步長和左右觸須的距離
step=eta*step
(20)
d=eta*d
(21)
其中,eta為步長與距離的衰減系數,一般設為0.95。
(4)循環(2)、(3)兩步直至找到最優解。
2.4 分數階混合蝙蝠算法
傳統的蝙蝠算法存在尋優精度有限,在較高精度要求下收斂偏慢,易出現局部最優等缺陷。為了提升傳統蝙蝠算法的尋優能力,克服其在搜索過程中易陷入局部最優的缺陷,本文將分數階微積分與天牛須搜索融合到傳統蝙蝠算法中,提出一種分數階混合蝙蝠算法(fractional hybrid bat algorithm,FHBA)。
2.4.1 分數階優化全局尋優
在傳統蝙蝠算法的全局尋優階段,基于分數階微積分擁有描述事件的記憶和遺傳特性這一特點,對蝙蝠的速度v求α階導數,使用新的速度更新公式來更新其位置的值,這時蝙蝠速度與位置的值就會遺傳和繼承其歷史狀態,使得全局搜索過程更加均衡。同時通過蝙蝠在尋優過程中的速度與位置來自適應調整導數的階次α。這樣能夠有效改善傳統蝙蝠算法出現局部最優的問題,在圖像閾值分割中也可以取得良好的效果。先將式(9)改寫為
(22)

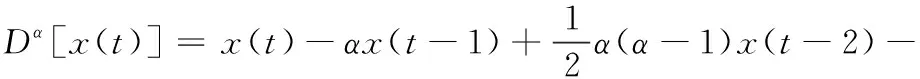
(23)
結合式(22),得到新的速度更新公式
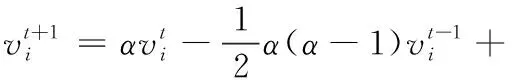
(24)
為了使階次α能夠自適應改變,本文從文獻[8]中引入進化因子f,根據蝙蝠速度和位置來不斷調整分數階次α,方法如下:
蝙蝠i與其它蝙蝠的平均距離為
(25)
上式N為蝙蝠的總數,D代表空間維度。
決定蝙蝠當前狀態的進化因子f表示為
(26)
上式中dg是蝙蝠的全局最優位置與其它蝙蝠距離的平均值,在所有dix中,最大值為dmax,最小值為dmin。由文獻[8]可知當階次α∈[0.5,0.8]時,收斂速度普遍較快。因此階次α的動態調節方式為
α(f)=1/2e-0.47f∈[0.5,0.8]
(27)
2.4.2 天牛須搜索改進局部尋優
通過對傳統蝙蝠算法缺陷的分析可知,算法的局部尋優階段是通過對當前的最優位置進行隨機變化來產生新的蝙蝠個體,導致后期種群多樣性不足。
而天牛須搜索擁有較為優秀的全局搜索能力,因此將其引入蝙蝠算法的局部更新階段,對傳統蝙蝠算法隨機產生的個體再次進行更新,豐富種群的多樣性。在蝙蝠算法的局部搜索階段,當蝙蝠的位置更新后,再將每一只蝙蝠視為天牛個體,并按照天牛須搜索進行更新,計算更新后的適應度并與更新前的適應度比較,若更新后適應度值更優,就進行更新,否則不更新。通過這樣的方式更新群體與個體的最優適應度,可以使群體的多樣性得到完善,加快達到最佳收斂點的速度。
改進后的局部更新為
(28)
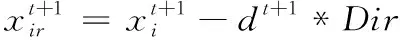
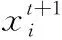
2.4.3 算法改進效果測試
為了驗證對傳統蝙蝠算法的改進效果,選擇常用的3個Benchmark測試函數對原始的蝙蝠算法(BA)和改進后的分數階混合蝙蝠算法(FHBA)進行測試,3個測試函數如下:
(1)Griewank函數
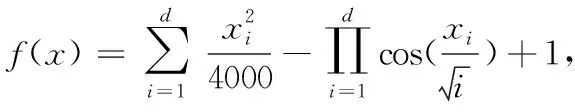
(2)Ackley函數
a+exp(1),此函數的取值范圍x∈[-32.768,32.768],函數中a=20,b=0.2,c=2π,理論最優適應度值為0,在x=0處取得。
(3)Rastrigin函數
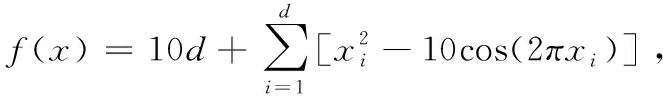
將函數維度d設置為10維,兩個算法的種群數為20,迭代次數1000次。Griewank函數的適應度曲線如圖1所示。
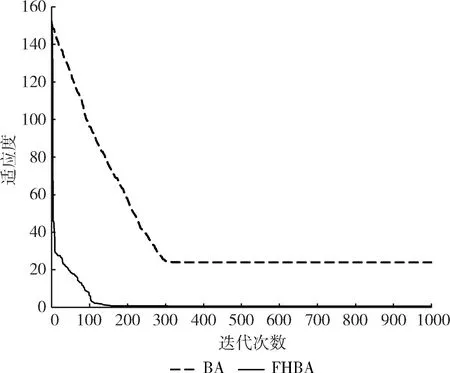
圖1 Griewank函數適應度曲線
Ackley函數的適應度曲線如圖2所示。
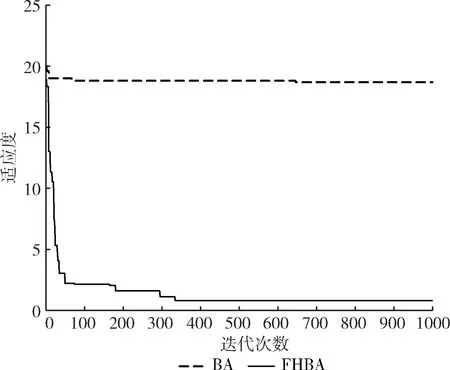
圖2 Ackley函數適應度曲線
Rastrigin函數的適應度曲線如圖3所示。
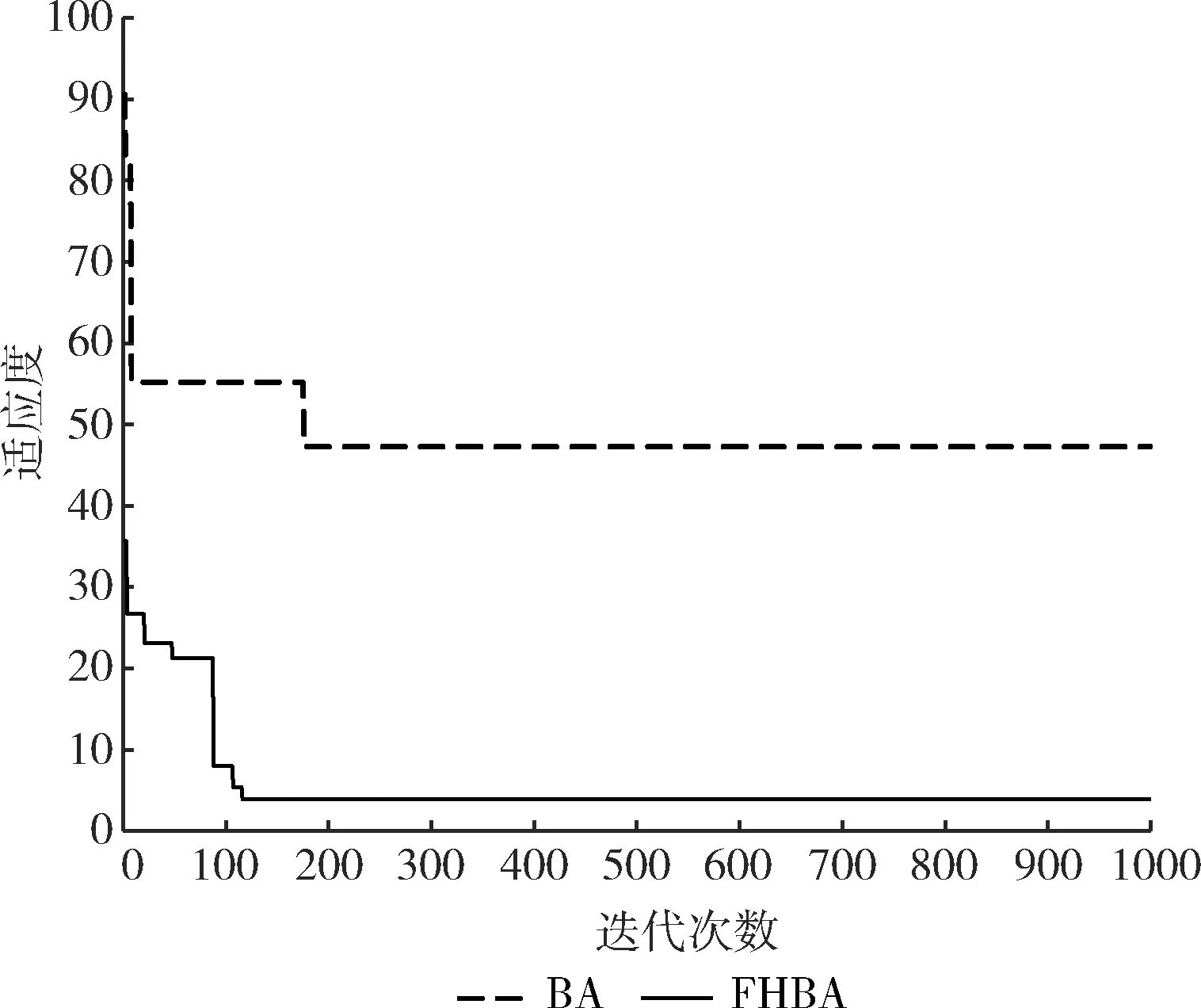
圖3 Rastrigin函數適應度曲線
由圖1可看出,原始的BA算法在前期收斂速度偏慢,在300次左右之后適應度曲線平行于x軸,說明算法陷入了局部最優,并且在后期難以跳出局部最優。在圖2中,原始BA算法在10次左右的迭代就出現了局部最優,在70次左右的迭代和650次迭代時,雖然有細微的變化,但也沒能夠跳出局部最優。從圖3來看,原始BA算法在前10次迭代中收斂速度很快,但在10次至180次左右和之后都是水平線段,說明算法陷入了局部最優,并且需要多次迭代來跳出局部最優。在3個函數的測試中,原始BA算法的尋優精度有限,易出現局部最優的問題。
在3個測試函數的適應度值曲線中,相較于原始的BA算法,通過在全局尋優中引入自適應分數階微積分,局部搜索中混合天牛須搜索的改進后的FHBA算法跳出了局部最優,有效提升了尋優精度。并且在圖1和圖3可看出改進后的算法對收斂速度也相對更快。
3 基于分數階混合蝙蝠算法的二維Otsu圖像分割
原始蝙蝠優化的二維Otsu圖像分割算法(BA-Otsu)存在分割精度低、收斂速度慢等問題,本文將改進后的FHBA算法與Otsu算法相結合,將二維Otsu算法的離散度矩陣作為FHBA算法的尋優函數,提出基于分數階混合蝙蝠算法的圖像分割(FHBA-Otsu),算法的具體步驟如下:
步驟1輸入待分割圖像,基于二維Otsu法生成目標函數;
步驟2初始化參數。種群數量N設為20,迭代次數Iter為100,蝙蝠位置xi,速度vi,音量Ai,脈沖發射率Ri,最小頻率fmin為0,最大頻率fmax為2,天牛須步長衰減系數eta設為0.95,左右觸須距離d為3;
步驟3將蝙蝠當前的位置向量視為待尋優的閾值,式(6)作為尋優目標函數,將位置向量帶入目標函數中計算出目標函數值最大時蝙蝠的位置。
步驟4按式(8)更新頻率,式(24)更新蝙蝠速度;
步驟5若rand>Ri,由式(28)更新蝙蝠位置,由式(20)、式(21)更新天牛步長和兩觸須距離;
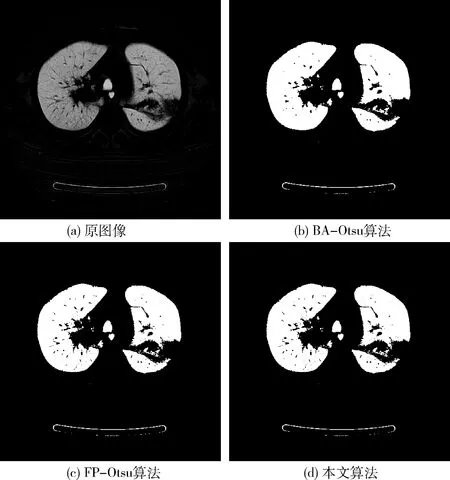
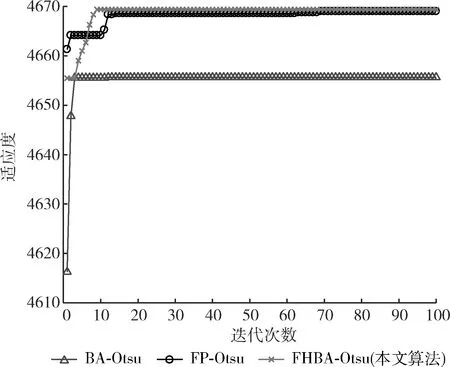
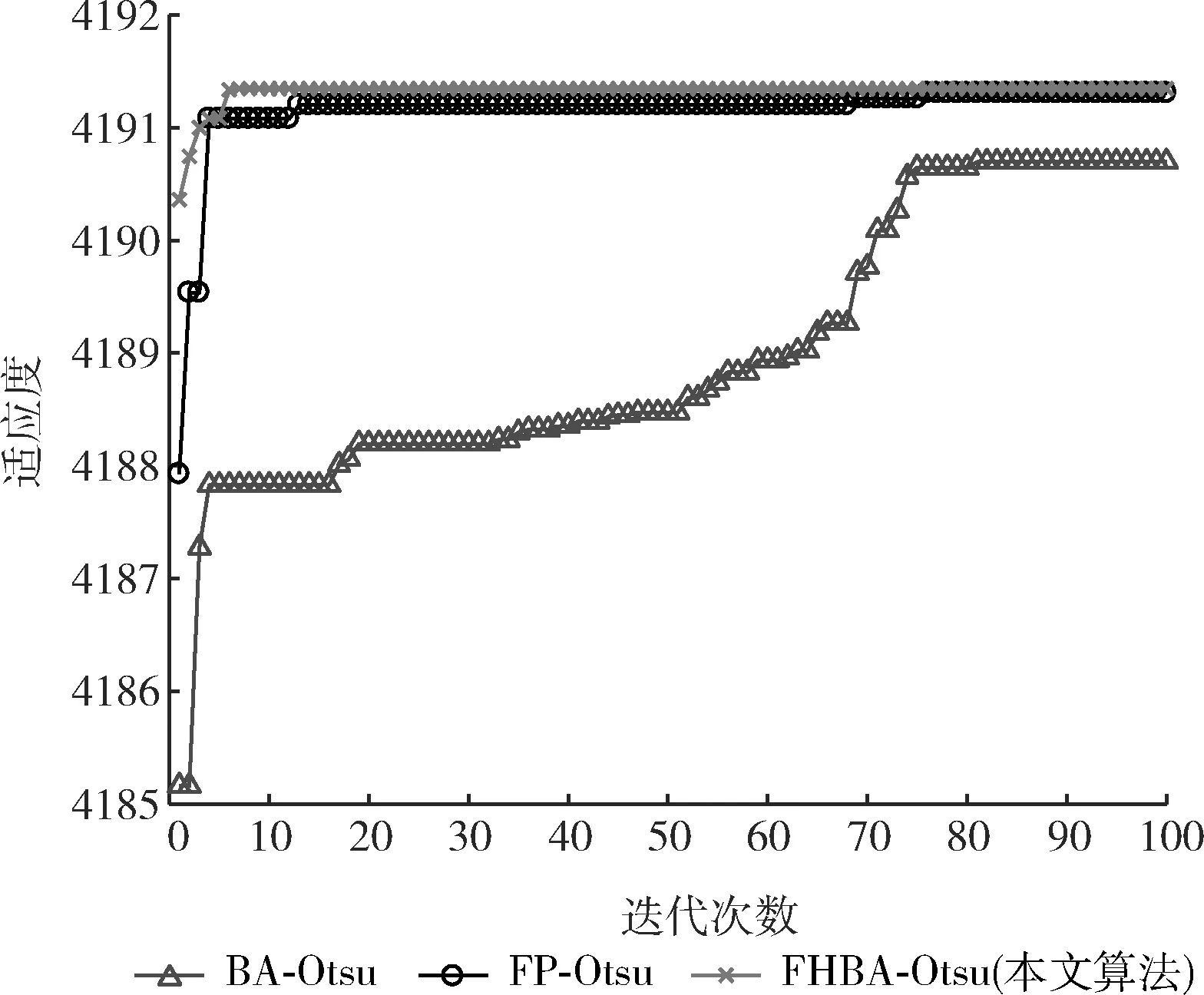
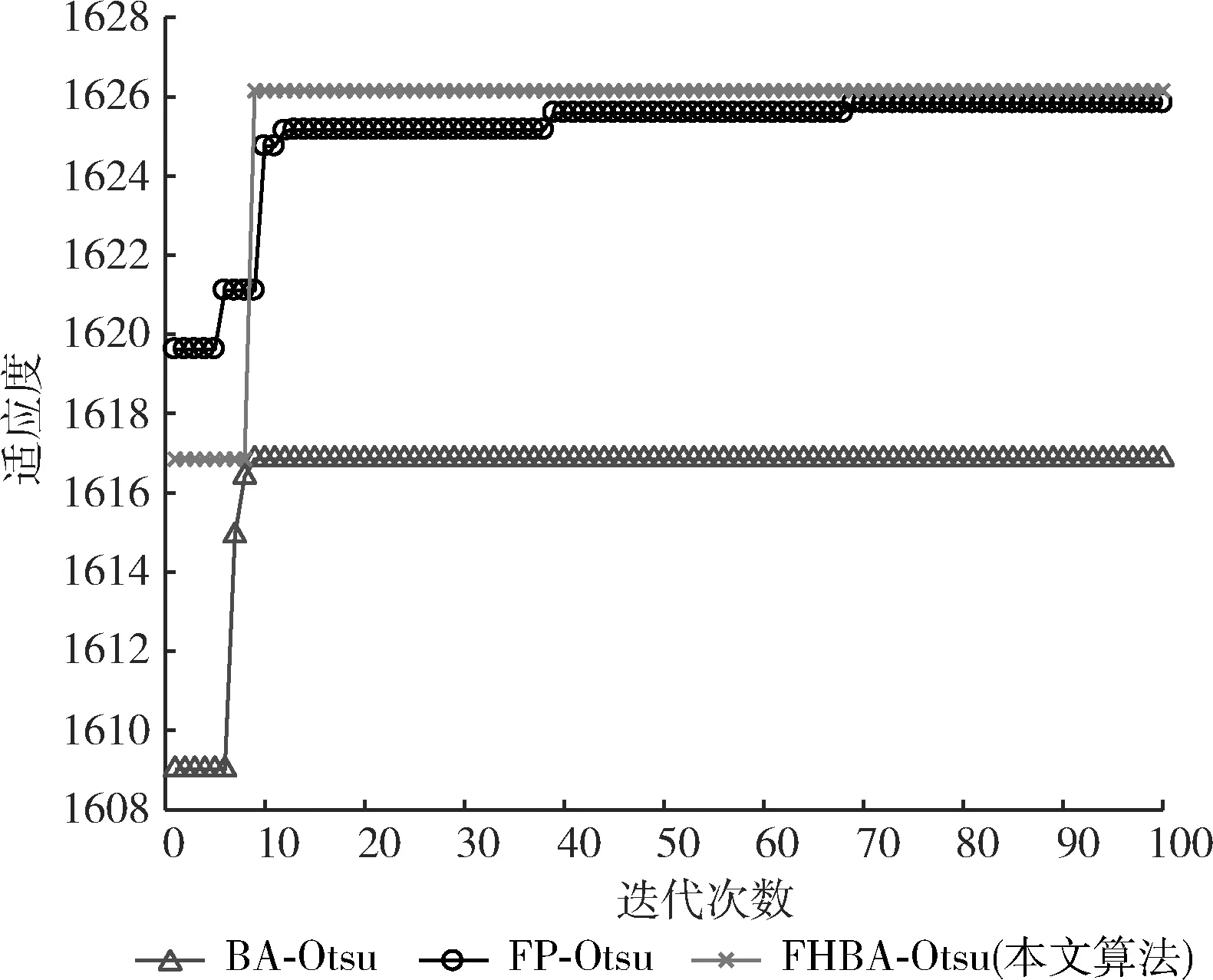
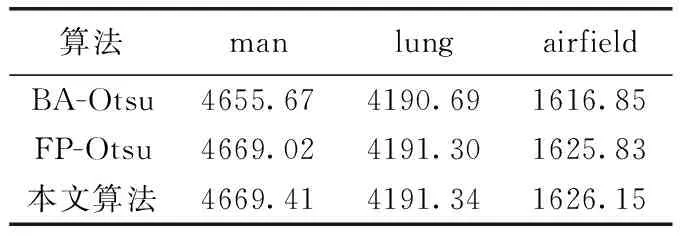
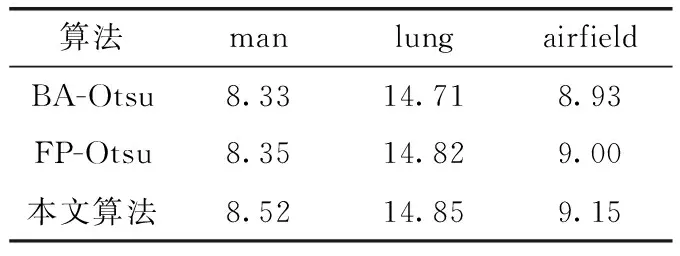
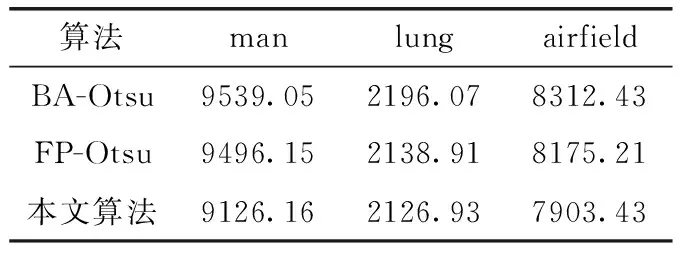
步驟6若rand 步驟7計算新位置的目標函數值并與步驟3相比較,更新全局最優位置; 步驟8判斷是否達到停止迭代的條件,達到則退出迭代,未達到則返回步驟4; 步驟9將輸出的最優位置(s,t)作為分割閾值進行二維Otsu圖像分割。 FHBA-Otsu算法流程如圖4所示。 圖4 FHBA-Otsu算法流程 為了驗證本文算法在收斂速度及圖像分割精度方面的改進,同時確保分割算法的健壯性,本文分別采用人物圖像man(320×320)、醫學肺部圖像lung(512×512)及機場圖像airfield(1024×1024)這3種不同類型的圖像進行實驗,并將本文提出的算法(FHBA-Otsu)與原始蝙蝠優化二維Otsu算法(BA-Otsu)、文獻[8]提出的分數階粒子群Otsu算法(FP-Otsu)進行對比分析。實驗的硬件環境采用Windows 10操作系統,Intel Xeon E3-1230 V2處理器(3.3 GHz),16 GB內存,實驗的軟件環境為MatlabR2016b。 通過適應度曲線完全收斂時的迭代次數來評價算法的收斂速度,收斂越快則速度越快。通過適應度值、峰值信噪比(PSNR)和均方誤差(MSE)這3個指標來評價圖像分割的精度。適應度值即為離散度測度值,適應度值越大分割效果越好。PSNR值越大,圖像的噪聲信息越低,說明分割圖像的抗噪性能更好,擁有更好的分割效果。MSE可理解為分割后的結果圖像與原圖像之間差異的期望[15],MSE的值越小,則圖像分割精度越高。 分割結果如圖5~圖7所示,首先對分割效果進行視覺上的對比,其次對各算法收斂速度進行對比,最后通過PSNR與MSE對3種算法進行對比。可以看出,本文算法在上述評價指標中均取得了良好的效果。 圖5 man圖像及其分割結果 圖6 lung圖像及其分割結果 圖7 airfield圖像及其分割結果 從圖像直觀效果上來看,對于man圖像的分割,BA-Otsu算法在人物胳膊、飾品、背景等區域分割過度,FP-Otsu算法在一些細節方面分割的不夠精確。相比較,本文算法保證了人物圖像細節部分的分割。對lung醫學圖像,BA-Otsu算法分割的器官組織不夠完整,FP-Otsu算法在一些微小細節上略有欠缺,本文算法分割出的器官組織結構更加清晰完整。對于airfield機場圖像的分割,相較于其它兩種算法,本文算法保留了更多的細節。 3種算法分割3幅圖像的適應度曲線如圖8~圖10所示。 圖8 man圖像適應度曲線 圖9 lung圖像適應度曲線 圖10 airfield圖像適應度曲線 從圖8中可直觀地看出,在對man圖像的分割中,BA-Otsu算法在4次左右迭代后就陷入了局部最優,FP-Otsu算法在65次左右完全收斂,本文算法在10次左右完成收斂。 從圖9可看出,在lung圖像的分割中,BA-Otsu算法在80次左右收斂,FP-Otsu算法在75次左右收斂,本文算法經過7次左右迭代完成收斂。 從圖10可看出,在airfield圖像的分割中,BA-Otsu算法在10次左右迭代后陷入局部最優,FP-Otsu算法經過68次迭代后收斂,本文算法在10次左右完成收斂。 從適應度曲線可看出,本文算法在克服了BA-Otsu算法易陷入局部最優的同時,提升了尋優的速度。 表1可看出,通過本文算法對3幅圖像分割的適應度值均要高于另外兩種算法,說明本文算法的分割效果更好。 表1 3種算法適應度值的對比 表2為3種算法分割3幅圖像的PSNR值,可看出本文算法的PSNR值高于其它兩種算法,說明分割后圖像的噪聲信息較少,抗噪性能更強,因此本文算法在圖像分割時受噪聲影響較少,保證了分割后圖像的質量。 表2 3種算法PSNR值的對比 表3為3種算法分割圖像的MSE值對比,從表中可看出,對于3幅圖像的分割,本文算法的MSE值均小于另外兩種算法,說明本文算法分割后的圖像精度相較另外兩種算法更具優勢。 表3 3種算法MSE值的對比 從上述實驗結果可看出,本文算法有效提升了圖像的分割精度。同時,本文算法在3幅不同背景、不同類型、不同復雜度、不同分辨率的圖像分割中均有著更好的分割精度與效果,說明本文算法不僅在單一類型的圖像分割上有著更佳的效果和更快的收斂速度,而是在3種常見類型圖像分割上都有著更加出色的表現,因此本文算法在對常見類型的圖像分割上具有良好的健壯性。 為了改善原始蝙蝠算法存在的易陷入局部最優、尋優精度不高、在較高求解精度下收斂速度慢等缺點,本文通過分數階微積分、天牛須搜索的特性來優化原始蝙蝠算法,利用分數階微積分的歷史記憶性優化蝙蝠的全局搜索過程,克服局部最優,提高其尋優能力,在蝙蝠的局部更新階段引入天牛須搜索,彌補后期種群多樣性不足導致的后期收斂速度問題,同時結合二維Otsu算法尋找最佳分割閾值,進行圖像分割。實驗結果可看出,本文算法相較于原始的BA-Otsu算法和文獻[8]的算法提升了圖像分割的精度與效果,有著更快的收斂速度與良好的健壯性。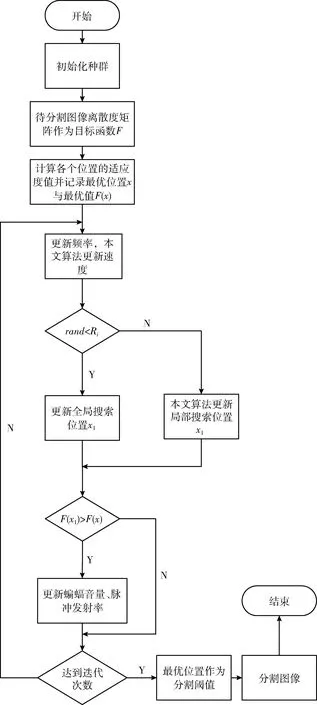
4 實驗結果與分析


4.1 分割效果對比
4.2 收斂速度對比
4.3 分割精度對比
4.4 分割算法健壯性分析
5 結束語

