基于2-階段成本優化的多播容量供應

杜文龍，黃 余

(1.江蘇電子信息職業學院 計算機與通信學院，江蘇 淮安 223003；2.圣路易斯大學 研究生院，菲律賓 碧瑤 2600)

0 引 言

網絡技術的進步和可用帶寬的增長導致了眾多媒體內容提供商提供數據傳播服務，如實時和按需媒體流。這些媒體內容提供商的一個主要關注點是網絡資源(即網絡容量)的供應；媒體內容提供商的要求以及對使用資源的付費通過服務級協議(service level agreements，SLA)[1,2]和因特網服務提供商(internet service providers，ISPs)獲得。超出SLA中規定限額的使用一般會引起高于SLA中最初商定的額外費用。由于客戶的未來需求本身是不確定的，所以媒體內容提供商的初始容量供應過程必須基于預期客戶使用模式和需求的預測對成本達成平衡。

由于多播利用了信息的可復制性，從而可獲得高效的帶寬利用和高吞吐量[3]。如果進一步利用網絡編碼，將使得多播路由算法是最優的和高效可計算的。對于有向和無向網絡中的多播來說，采用網絡編碼會得到更高的吞吐量以及更便宜的路由成本[3,4]。此外，還可以采用線性規劃(linear programs，LP)來計算高效多播。

已有大量文獻研究了不同情形下通信網絡的容量規劃。文獻[5]提出了一種用于需求不確定時的容量規劃算法；文獻[6]針對面臨不確定性流量需求時需要提前預留最佳帶寬的虛擬專用網絡(virtual private networks，VPN)客戶，提出了一種基于隨機規劃模型；文獻[7]通過對不同場景下網絡資源分配方法進行需求分析，提出了完全壟斷和完全競爭的網絡資源分配模型；文獻[8]提出并分析了一種基于定價的收入管理模型，同時針對隨機需求提出了一種基于動態規劃的解決方案。

也有不少文獻對隨機優化進行研究。文獻[9]采用隨機優化理論對異構網絡中的若干關鍵問題進行了研究，同時介紹了隨機優化中采用的一些技術和模型；近年來，隨機優化問題還受到了計算機理論界的廣泛關注。文獻[10]對各種經典組合優化問題的各種隨機形式進行了研究；文獻[11]將LP四舍五入用來得到隨機Steiner樹問題的常數因子近似；文獻[12]采用了一種新的原始對偶技術來求解隨機環境中尋找最優Steiner森林的問題。

資源供應最主要的挑戰是未來需求的不確定性，因此，本文假設存在一個概率分布，這個概率分布可以用來估計對多播服務感興趣的未來客戶集，于是將采用網絡編碼的多播容量供應問題建模為一個2-階段隨機優化問題，目標就是設計指導在第一階段容量購買決策的算法，從而使得兩個階段的總體成本在預期中最小化。

1 預備知識

將通信網絡建模為一個圖G=(V,E,C,w)， 其中V是節點的集合，E是邊的集合，C和w分別為容量和成本向量。邊e∈E有固定容量C(e)， 以及相關的每單位流量成本w(e)。

假設一個固定的源節點s∈V為多播接收者集合T?V提供多播服務。要研究的問題是采用網絡信息流時，對隨機環境中一個給定的數據速率，最優化其多播成本。多播流是一個向量f∈Q+E， 其中Q+是非負有理數集合。假設期望的多播(數據)吞吐量為d，目標是得出一個流量路由方案，使得多播服務的總成本最小化。假設e∈E的每單位流量成本為w(e)， 用W(T) 表示服務集T的多播最優成本，多播成本函數對于有向網絡是次可加性的，即對于不相交集合A,B?T， 滿足

W(A∪B)≤W(A)+W(B)

(1)

網絡編碼結果表明，當且僅當一個速率d是從源分別到每個接收者的可行單播速率時，d的多播速率就是可行的[13,14]，即如果能在獨立單個的會話中得到每個接收者的速率d的單播流，則該速率的多播流也存在。這樣，可以把有效多播看作是從源到每個接收者的概念單播流的結合，因而可以通過線性規劃來計算概念單播流的有效結合。

假設每個接收者t∈T都有一個通往源的路徑集合Pt。對于路徑p∈Pt，用f(p)表示沿p從s到t的概念流，用f(e)表示邊e上的真實流，則可以通過下面的LP計算最小的多播流成本

Minimize： ∑ew(e)f(e)

(2)

滿足

∑p∈Ptf(p)=d?t

(3)

f(e)≥∑p∈Pt∶e∈pf(p) ?e,?t

(4)

C(e)≥f(e) ?e

(5)

f(e)≥0；f(p)≥0 ?e,?p∈Pt,?t

約束條件式(3)要求全部多播接收者必須獲得d的流速率。每個邊上的真實流是采用該邊的全部概念流的最大值，即

f(e)=maxt∑p∈Pt;e∈pf(p)

(6)

盡管max(·)函數是非線性的，但約束條件式(4)等價地給出了優化方向，最后，每個邊上的流量必須遵從容量約束條件式(5)。

圖1 不采用網絡編碼與采用網絡編碼的成本比較

2 基于2-階段成本優化的隨機多播

2.1 最優多播模型

這部分建立一個隨機環境下的最優多播模型。如前所述，本文研究的隨機多播問題包括2個階段。在第一階段，得到潛在多播接收者集合T的概率分布，這些分布基于市場預測或歷史客戶使用模式；在第二階段，將此建模為真實的多播接收者集合A的實現。對于一個接收者t∈T，令P(t) 為t在第二階段將要訂閱的多播服務的概率，并假設這些概率是獨立的，即?t,t′∈T，P({t,t′}?A)=P(t)P(t′)。 定義一個膨脹參數λ，它使得在第二階段中邊e的成本從w(e)增加到λw(e)，這相當于使用了超過SLA規定限額而引起的更高價格。目標就是在第一階段要明智地購買容量，使得在第二階段中對于多播集的所有可能實現A?T的期望總成本最小化。令g∈Q+E為在第一階段購買容量的向量，hA∈Q+E表示當集合A實現時在第二階段所需要的額外容量的向量，定義

P(A)=∏t∈AP(t)∏t?A(1-P(t))

(7)

則可以將2個階段的最小化期望成本構建為一個LP

Minimize： ∑ew(e)g(e)+∑e∑A?TP(A)λw(e)hA(e)

(8)

滿足

∑p∈PtfA(p)=d?t∈A,?A

(9)

fA(e)≥∑p∈Pt∶e∈pfA(p)?e,?t∈A,?A

(10)

C(e)≥fA(e) ?e,?A

(11)

g(e)+hA(e)≥fA(e) ?e,?A

(12)

g(e),hA(e),fA(e),fA(p)≥0 ?e,?p∈Pt,?t∈A,?A

LP式(8)計算服務集A的全部可能實現的最小期望成本即最優解。前3個約束條件表明，對于每個集合A?T，網絡編碼多播的可行性要求必須滿足，最后的約束條件表明，在2個階段購買的容量數量必須足以容納服務集A的多播流fA。

在獨立分布概率的情況下，存在指數級的多個集合A，而且直接用LP式(8)計算最優向量g*是很難的。因此，下面提出2種算法來指導第一階段的購買，使得總成本接近通過LP式(8)計算得到的最優解成本。

2.2 啟發式算法

算法基于以下前提：由于容量因因子λ而變得更昂貴，直觀上，如果e上需要c的概率大于1/λ，則可以通過在e上購買容量c來最小化預期成本。

具體來說，假設T是潛在接收者集合，令f為從源到T的全部成員的最優最小成本流。對于每個邊e，令ft(e)為該邊上從s到一個特定接收者t∈T的總的概念流。由于概念流不競爭帶寬，因此，全部接收者在每個邊上就存在k≤|T| 個不同級別的總的概念流。用li表示邊e上的級別為i∈{1,2,…,k} 的總流量，不失一般性，假設這些級別按總流量的降序排序，即li+1li的接收者t出現的概率，這相當于沒有從子集Ti-1(e) 中得到未來接收者的概率。更準確地說，用P≤(li,e) 表示邊e需要至多li個單位流的容量的概率，同樣，P≥(li,e) 為邊e需要至少li個單位流的容量的概率，則P≤(li,e) 可計算為

P≤(li,e)=∏j∈Ti=1(e)(1-P(j))

(13)

此外，還有

P≥(li,e)=1-P≤(li+1,e)

(14)

可見，在預期中，無論概率P≥(li,e) 是否大于1/λ，當單獨考慮這個邊時，通過購買等于li個單位流量的容量可以使得成本最小化。

將網絡中的每個邊應用上面的算法思想，其偽代碼實現如算法1；算法首先計算最小成本流f，然后檢查每個邊上不同的概念流級別。然后，算法建議當且僅當P≥(li,e)>1/λ時對于邊e購買等于li個流量單位的容量。

算法1： 啟發式算法

Input： 潛在多播接受者集合T,t∈T的訂閱概率P(t)， 網絡圖G(V,E,C,w)

Output： 在第一階段要購買的容量向量g∈Q+E

(1)在T上運行LP式(2), 令f為得到的流;

(2)g(e)∶=0,?e∈E;

(3)for eache∈Edo

(4) for eacht∈Tdo

(5)ft(e)∶=∑p∈Pt∶e∈pf(p);

(6)F(e)∶={ft(e)|ft(e)>0};

(7) 對F(e)排序, 令l1,…,lk為e上概念流級別的降序;

(8)Ti(e)∶={t|ft(e)≥li} ?i∈{1,…,k};

(9) for eachi∈{1,…,k} do

(10)P≤(li+1,e)∶=∏j∈Ti(e)(1-P(j));

(11)P≥(li,e)∶=1-P≤(li+1,e);

(12) ifP≥(li,e)>1/λthen

(13)g(e)∶=li;

(14) end

(15) end

(16)end

(17)輸出g

圖2 啟發式算法導致沒有恒定約束的示例網絡

在這個示例中算法1性能較差，因為在初始最小成本流計算中沒有考慮接收者的概率分布。這就要求求解方法需要考慮初始流計算階段的分布。因此，下一節提出一種基于采樣的方法，為預測未來情形提供一種更準確的方法，并在理論上具有可證明的性能保證。

2.3 采樣算法

下面首先給出具體的采樣算法，然后證明它的性能約束。

2.3.1 采樣算法

算法2： 采樣算法

Input： 潛在多播接受者集合T,t∈T的訂閱概率P(t)， 網絡圖G(V,E,C,w)

Output： 在第一階段要購買的容量向量g∈Q+E

(1)Λ∶={?};

(3)Ai={?};

(4) for eacht∈Tdo

(5)r∶=[0,1] 中的隨機數;

(6) ifr≤P(t) then

(7)Ai∶=Ai∪{t};

(8) end

(9) end

(10)Λ∶=A∪Ai;

(11)end

(12)在Λ上運行LP式(2), 令f*為最優最小成本流向量;

(13)for eache∈Edo

(14)g(e)=f*(e);

(15)end

(16)輸出g

在第二階段，一旦接收者的真實集合S已知，就需要用服務集合S所需的額外容量來增加第一階段的解。對于每個邊e，用兩個邊e′和e″替換它。設e′的容量為g(e)，成本w(e′)=0， 并將剩余容量和初始成本分配給e″，即C(e″)=C(e)-g(e) 且w(e″)=w(e)， 則在這個新圖上計算得到的最小成本是集合S/Λ對Λ增加的成本，用WAUG(Λ,S/Λ) 表示。

盡管算法本身相對簡單明瞭，但關鍵在于證明算法有一個好的性能約束。為此，首先引入成本分攤方案的概念。成本分攤方案是將多播解的成本分配給接收者集合的一種方法。具體說，給定一個最優多播算法AM，它計算一個接收者集合A的多播成本，則成本分攤方案ξ：2V×V→R≥0將成本份額ξ(A,t) 分配給每個接收者t∈A。

定義1 設AM是一個計算多播最優最小成本的算法，ξ(·,·) 是相關的成本分攤方案，則對于任意兩個不相交接收者集合A,B?T來說，如果以下3個屬性都滿足，稱ξ(·,·) 為β-嚴格的成本分攤函數：

(1)ξ(A,t)>0僅當t∈A；

(2)∑t∈Aξ(A,t)≤W(A)；

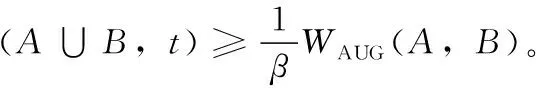
前兩個屬性在博弈論中分別稱為個體理性和預算平衡[15]。第一個屬性表明，如果一個多播接收者沒有接收到服務，則不應當要求它支付。第二個屬性表明，收到的支付總額不應超過解的成本。最后一個屬性關系到集合B中接收者在集合A∪B中被服務時的成本分攤，即將B增加到A的現有解的成本。如果β-嚴格的成本分攤關于算法AM存在，則B中接收者的成本分攤應該至少涵蓋集合A的多播解的增加成本的1/β。β-嚴格的成本分攤確保了增加的成本可以受到這些成本分攤的約束，因此，改用符號將∑t∈Bξ(A∪B,t) 表示為ξ(A∪B,B)。 下面來表明算法2的性能約束。

定理1 給定一個采用網絡編碼的多播最優最小成本的相關β-嚴格的成本分攤函數，算法2構建了一個采用2-階段隨機多播問題的(1+β)-近似解。

由于篇幅所限，這里不給出該定理的證明過程。

注意，算法2未明確采用成本分攤方案。性能約束的證明只需要存在某個β-嚴格的成本分攤方案，它可以與用于計算最優多播流的算法相關聯。因此，本文的目標是證明成本分攤的存在，特別是對于網絡編碼多播是嚴格的，并且有有界的嚴格因子β，這樣才能表明算法2是隨機多播問題的一個很好的解決方案。對于任意兩個不相交集A,B?T， 以及一個給定的成本分攤方案β(·,·)， 可以將β定義為

(15)

2.3.2 平均成本分攤是O(|T|)-嚴格的

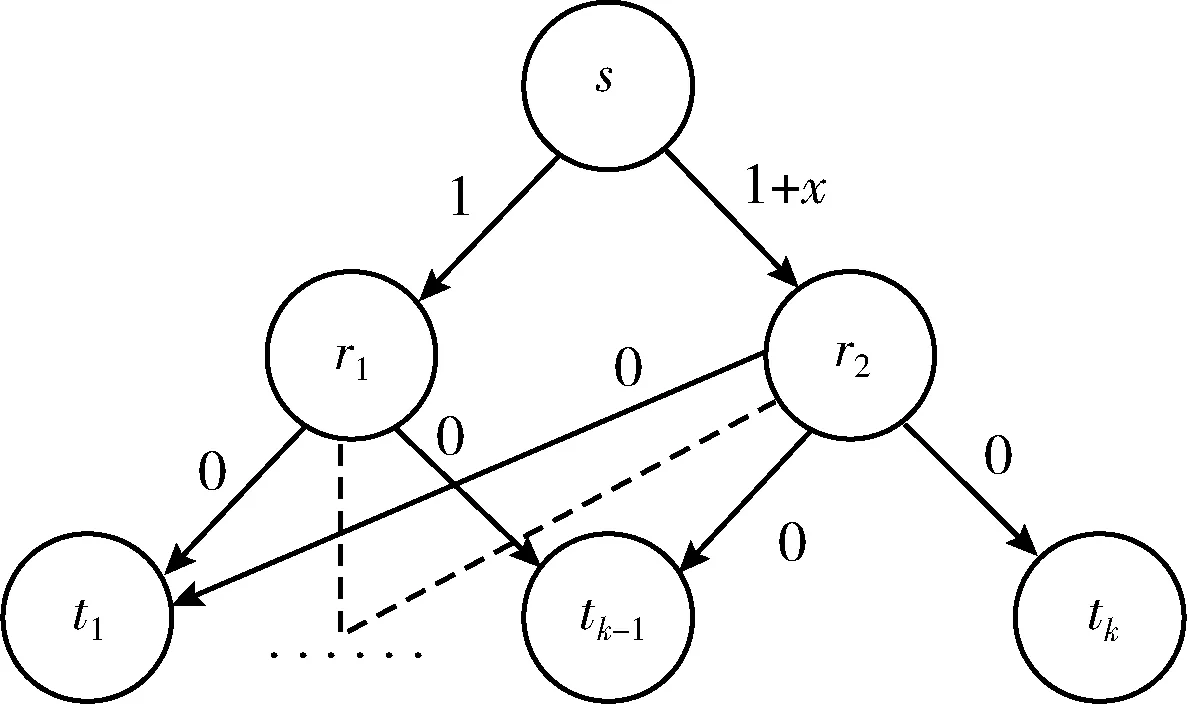
圖3 平均成本分攤導致無約束嚴格因子的網絡(這時β=k)

(16)

因此，增加的成本為kξ(T,tk)， 這意味著β=k=O(|T|)。 因此，平均成本分攤對于證明采樣算法的約束來說不是一個可行的候選方案。

2.3.3 成本分攤的LP對偶解是2-嚴格的

LP式(2)的對偶線性規劃為下列最大化問題

Maximize： ∑txtd-∑eC(e)s(e)

(17)

滿足

∑tyt(e)≤w(e)+s(e) ?e

(18)

xt≤∑e∈pyt(e) ?p∈Pt,?t

(19)

xt<>0；yt(e)≥0；s(e)≥0 ?t,?e

在對偶LP中，變量xt、yt(e)和s(e)分別對應于原始LP式(2)中的約束式(3)～式(5)。將對偶最優解表示為 (x*,y*,s*)。 具體來說，如果無限小流量單位是一個非合作多播路由博弈中的自私代理，則基于對偶變量的成本分配方案就能確保最優最小成本流是納什均衡。因此，對偶解成本分攤方案在非合作網絡環境中執行最優多播流。

(20)

因此，變量xt表示t的每單位流量成本，這樣，每個接收者的總成本為xtd。但這種成本分配方案只在成本度量w(e)下是預算平衡的，也就是說，如果用成本w(e)+s(e) 替換每個邊的成本w(e)，且W′(T) 是該新度量下的最小多播流的成本，則成本分配方案就是預算平衡的，因此∑t∈Txtd=W′(T)。 下面來證明這樣的成本分攤方案是2-嚴格的。

令W(T)為由LP式(2)計算得到的接收者集合T的最優流量成本，考慮下列線性規劃

Minimize： ∑ew(e)f(e)

(21)

滿足

∑ew(e)f(e)=W(T)

(22)

∑p∈Ptf(p)≥d?t

(23)

f(e)≥∑p∈Pt∶e∈pf(p) ?e,?t

(24)

f(e)≥0；f(p)≥0 ?e,?p∈Pt,?t

在總成本等于W(T)下，LP式(21)使得多播流成本最小化，即目標函數為W(T)。式(21)的對偶LP如下

Minimize： ∑txtd+βW(T)

(25)

滿足

xt≤∑e∈pyt(e) ?p∈Pt,?t

(26)

∑tyt(e)≤(1-β)w(e) ?e

(27)

β<>0；xt≥0；yt(e)≥0； ?t,?e

下面的引理表明，LP式(25)中的對偶向量x構成了一個有效的成本分攤方案，該方案關于W(T)是預算平衡的。

引理的證明可以直接從LP的對偶性得到。因為兩個LP的目標函數有相同的最優解值，因此，具有所述性質的解一定存在。事實上，如果在具有無限邊容量的網絡中最小成本流更便宜，則對于LP式(25)的每個最優對偶解，可得到β=0。下面給出有效的成本分攤方案。

定義2 令 (x*,y*,β*) 是對于接收者集合T、多播速率為d的LP式(15)的任意最優解，這樣β*=0， 則定義成本分攤方案為

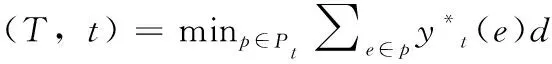
(28)

成本分攤方案ξ(·,·) 是一種有效的成本分攤方案，因為它是預算平衡的，而且不在多播集中的接收者有零成本。

下面表明分攤方案ξ(·,·) 是2-嚴格的，它基于以下3個引理，引理的證明略。

引理2 在網絡編碼多播中，成本分攤方案ξ(·,·) 對于任意兩個不相交集合A和B，ξ(A∪B,A)≤W(A)；

引理3ξ(A∪B,B)≥W(A∪B)-W(A)；

引理4W(A∪B)-W(A)≤WAUG(A,B)≤2(W(A∪B)-W(A))。

由上面3個引理可以得到下面的定理。

定理2 LP式(17)的對偶變量定義了2-嚴格的成本分攤。

證明：由于成本分攤只適用于多播接收者，因此要尊重個體理性，根據定義，成本分攤也是預算平衡的。根據引理3和引理4得到

(29)

證明完成。

作為成本分攤的對偶變量的嚴格因子的上界顯然是2。現在通過考慮圖1所示的網絡來給出β的下界。假設目標多播率為1，可以發現對偶變量定義了在這種情形下唯一的成本分攤，例如ξ(T,t1)=1.5， 其中T={t1,t2,t3}。 此外，WAUG(t2∪t3,t1)=2， 因此β=2/1.5=1.333。

定理1和定理2為采樣算法提供了理論上的性能保證。

3 算法仿真結果及分析

3.1 仿真環境及設置

仿真在采用C++的BRITE[16]網絡拓撲生成器隨機生成的網絡上進行。BRITE是一種用于生成與Internet非常相似的拓撲工具，它可以用自頂向下和自底向上兩種方法來產生GT-ITM層次模型，同時可為多個網絡模擬程序提供接口，如NS-2、SSF、Omnet++和Jsim等，并支持可視化工具Otter；BRITE能生成路由器層、AS層以及分層結構拓撲圖，并可為連接分配帶寬和延遲，具有可視化用戶接口；我們在算法中隨機分配邊容量和成本值，源節點和多播接收者集合也隨機選擇。除非特別說明，全部接收者都按均勻分布隨機分配一個訂閱概率。在第一階段，根據算法1和算法2的建議購買容量，在第二階段，用接收者的訂閱概率隨機生成真實的接收者集合，并以膨脹因子為λ的價格購買額外的容量。得到的每個數據點是重復實驗200次并取平均值的結果；為了表明本文算法的性能，將通過LP式(8)得到的最優解作為比較基準，并與文獻[8]的基于網絡收益最大化的定價管理模型的成本解進行比較。

3.2 仿真實驗結果

圖4為對于不同網絡大小和不同多播接收者數量得到的不同算法的解成本，其中膨脹參數λ設置為5。可見，對于不同網絡大小時，本文提出的兩種算法與最優解非常接近，甚至在某些情形下還優于最優解。對于不同多播接收者數量時(這時網絡大小固定在100個節點)，啟發式算法始終優于最優解；還可看到，在兩種情形下，啟發式算法略優于采樣算法，而且在兩種情形下，本文的兩種算法始終優于文獻[8]的方案。

圖4 不同算法得到的解成本比較

圖5為膨脹參數λ對兩種算法性能的影響。對于小的λ值變化，如圖5(a)所示，兩種算法的性能與最優解的差都在10%以內，基本不受λ值的影響；隨著膨脹參數的不斷增大，如圖5(b)所示，兩種算法的性能基本都能收斂到最優解。這是因為當第二階段的成本增大時，兩種算法都能為第一階段的全部接收者集合提供最優解。

圖5 膨脹參數λ對算法1和算法2性能的影響

由前面分析知道，啟發式算法在初始最小成本流計算中不考慮接收者的概率分布，從而在某些情形下可能運行很差，而采樣算法考慮了接收者的概率分布，為預測未來情形提供了一種更準確的方法，并具有理論上的性能保證。為了比較兩種算法，我們將訂閱概率在范圍[0,0.1]內均勻抽取，網絡大小由100個節點構成，有10個多播接收者且設置λ=10；圖6為通過啟發式算法和采樣算法得到的解成本。可以看到，兩種算法的解都接近最優解，但采樣算法的性能要優于啟發式算法。原因是啟發式算法最初計算全部接收者的最優多播流，可能最終在更昂貴的邊上購買容量，另一方面，當在計算第一階段的目標多播集時，采樣算法通過考慮訂閱概率來求解這個問題；還可看到，隨著極低訂閱概率的接收者數量的增加，與采樣算法相比，啟發式算法的性能受到的影響越來越大。

圖6 不同訂閱概率接受者數量對算法性能的影響

圖7 采樣輪數對采樣算法性能的影響

4 結束語

由于互聯網數據傳播服務的普及以及內容提供商和ISPs之間的SLA商業模式，明智的多播容量規劃使得其自身成為一個重要的研究方向；本文將具有不確定性的多播容量規劃構建為一個具有追加的2-階段隨機優化，提出了2種解決方案，即利用網絡編碼優勢的啟發式解決方案和進一步結合采樣技術的改進方案。仿真結果表明，2種解決方案的實際性能接近最優解的性能。

盡管本文的研究為采用網絡編碼的多播容量規劃問題提供了新的見解，但仍存在一些局限性。本文的解決方案更適用于替代網絡，如無線Mesh網或大規模無線Ad-hoc網絡，所以將本文的研究擴展到更好的內容分發模型系統是未來研究的一個重要方向；此外，本文的研究只考慮了在所有網絡鏈路的成本一致增加的情況，且只有一個不確定的階段，還存在非均勻的成本增加，以及多播接收者可以動態訂閱和離開多播會話的多個階段，這些都是我們未來研究的內容。