基于物理模型的海浪真實感模擬研究

朱天惠，任鴻翔，趙玉然

(大連海事大學航海動態仿真和控制交通行業重點實驗室，遼寧 大連116026)

1 引言

航海模擬器的高速發展為航海院校及科研院所培養輸送大批高素質海員提供了堅實的基礎。航海模擬器的優劣主要體現在功能或稱為適任能力、物理真實感、行為真實感和操作環境真實感等幾個方面。視景系統是近年來航海模擬器發展最快的部分之一，是模擬器研制成功與否的關鍵技術，其主要體現在提升模擬器的操作環境真實感[1]。

航海模擬器中海浪約占整個視景的一半區域，其模擬的逼真與否對環境真實感影響較大。現階段航海模擬器中有關海浪的模擬主要采用的是基于構造的方法，該方法主要包括基于幾何模型的方法和基于統計和譜的方法。基于構造的方法的優點是實時性較強，缺點是真實感較差，難以展現流體細節，而且在較高視點處觀察海浪，磁磚效應比較明顯[2]。

隨著計算機硬件設備的高速發展，圖形處理器的計算速度大大加快，基于物理模型的方法逐漸步入視野。基于物理模型的海浪繪制方法現階段主要分為歐拉網格法(Grid-basedEulerian Approach)以及拉格朗日粒子法(Particle-based Lagrangian Approach)歐拉法通過固定網格單元來模擬流體在單元上的移動，其缺點是易受時間步長條件限制，且當網格分辨率增加，真實感較強時，限制效果會更明顯。拉格朗日法則通過分析流體質點在任意時刻的速度、運動軌跡、密度、壓力等物理量，計算機圖形學中使用粒子來表示質點，通過粒子來離散控制方程。拉格朗日法的優勢在于模擬真實感較強，且可以在三維空間模擬例如水花、泡沫等更加豐富的流體細節、處理更加復雜的流體表面[3]。常用的拉格朗日方法有SPH(SmoothedParticleHydrodynamics)方法以及PBF(PositionBasedFluids)方法等。因為PBF方法相比較傳統SPH方法，具有允許大時間步長，實時性較好等特點，基于位置的流體繪制方法成為海浪仿真研究的熱點。Müller等[5]最先提出PBD(PositionBasedDynamics)框架，并用來模擬布料。Macklin[5]等首次將PBD框架用于流體模擬，提出一個融合了密度迭代求解器的PBF框架，實現了與當前SPH求解器接近的不可壓縮性和收斂性，穩定性強，時間步長大，適合實時渲染[3]。Kang等[6]通過構建無散速度場，加快收斂速度。K?ster等[7]提出一種自適應迭代的APBF(Adaptive PBF)方法，適用于更大場景流體實時模擬。

結合上述分析，綜合考慮物理海浪流體建模方法，提出一種基于位置動力學的海浪真實感模擬方法。主要通過構建PBF流體模型，利用渦度約束函數進行Curl運算求解粒子的旋度場，再根據所求得的旋度場與位置向量進行計算，得到渦度力場，最后根據力場所得旋向加速度實時更新流體粒子的速度，從而實現實時的真實感海浪模擬。

2 流體模型構建

PBF方法是一種基于PBD框架下的無網格、拉格朗日粒子法。PBD框架的本質是構建約束條件，然后通過對約束條件進行投影，更新流體粒子的位置信息，并借此更新速度值。PBF作為基于PBD框架的流體模擬方法，通過構建密度約束，迭代求解流體粒子的位移偏量，根據位移偏量，實時更新流體粒子的速度，再將流體粒子繪制出來。

2.1 基于位置的動力學框架

傳統方法通過求解力的值，再根據力的值進行數值積分，從而更新速度值。與傳統的基于力的求解方法不同，基于位置的動力學框架采用的是約束的手段。在PBD方法中，當檢測到兩個物體發生穿透時，直接根據所采用的約束條件修正物體的位置，再更新物體的速度信息。PBD框架[4]算法如表1所示：

表1 基于位置的動力學框架算法

基于位置的動力學框架核心在于第7)～15)行。第7)行通過顯式歐拉積分方法估算物體頂點的新位置，9)～11)行是一個迭代解算器，通過采用高斯-賽德爾迭代的方法反復進行約束投影來控制估算位置從而保證位移滿足約束條件。通過公式可以表示為：

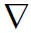
(1)

在13)、14)行，物體頂點移動到了最佳估算位置，速度也隨之更新，速度的控制通過第5)、6)及16)行實現。無法轉換為位置約束的外力通過第5)行進行速度更新，系統只考慮重力對物體的影響，所以合外力與質量倒數的乘積等于重力加速度。第6)行用于特定情況下添加速度阻尼，第16)行根據摩擦系數和補償系數調整碰撞頂點的速度。

2.2 PBF流體模型

通過與傳統SPH插值方法結合，Macklin等人[5]提出一種基于PBD框架下的流體模擬方法PBF。不同于傳統PBD框架用于解決固體問題而采用的位置約束，PBF方法通過計算流體質點的密度，采用一種密度約束方法來更新流體質點的位置。PBF粒子系統建模流程如圖1所示。

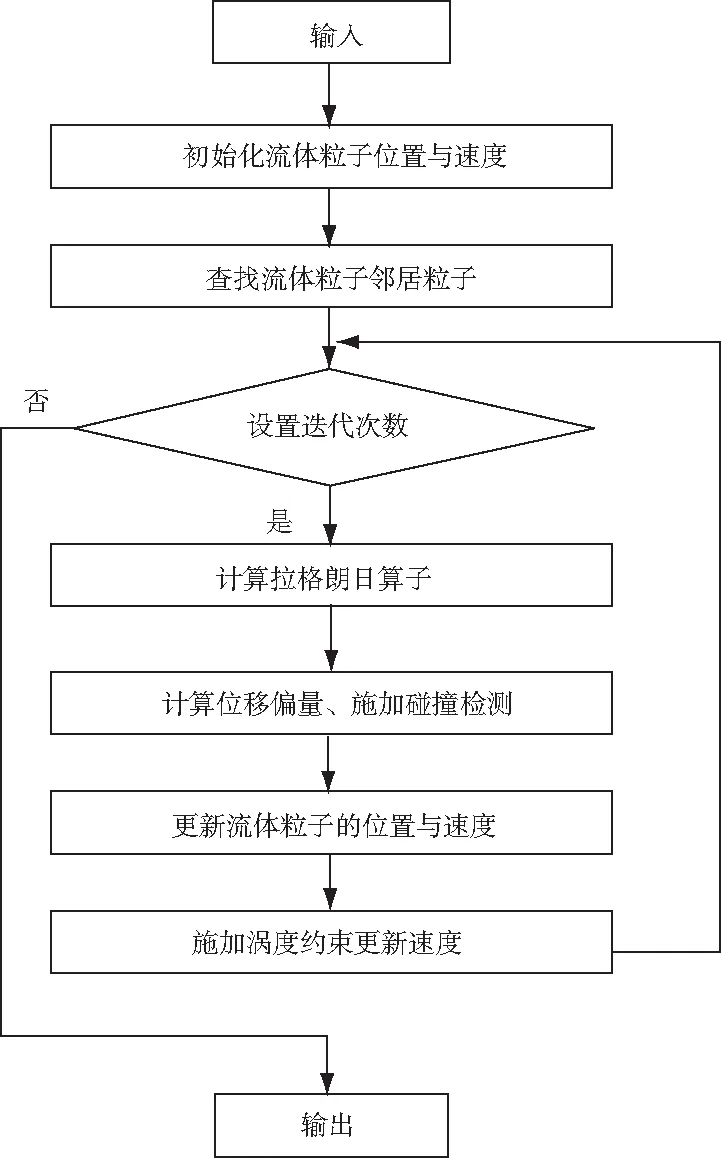
圖1 PBF粒子系統建模流程

為保證流體的不可壓縮性，針對每一個流體粒子，都需要滿足密度約束條件

(2)

式中，ρ0是靜態密度，ρi通過標準SPH密度估算器給出

(3)

在流體模型中，認為所有的流體粒子擁有均等的質量，所以后續公式中舍掉質量項mj。式中W為光滑核函數，根據Muller[8]首次將SPH方法用于模擬流體時采用的核函數，本文選用Poly6核函數用于密度估算，選用Spiky核函數用于梯度計算，核函數如下

(4)

(5)

Monaghan等人。給出了在粒子層面上的梯度公式，將其用于密度約束，可以得到對于任意流體粒子k的約束條件的梯度為

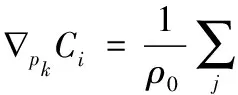
(6)

梯度公式隨著流體粒子的類型不同而產生變化，流體粒子k可分為對象粒子以及鄰域粒子

(7)

將其帶入到式(1)，可以求得式中拉格朗日算子λ的值為

(8)

每個流體粒子都具有拉格朗日算子λ，算子的值對于同一流體模型中的所有流體粒子都是相同的。

因為式(2)中的約束條件是非線性的，且在光滑核函數的邊界梯度逐漸消失。這會導致所求得的拉格朗日算子在分母無窮小時的不穩定。根據Smith提出的混合約束力理論，可以在密度約束階段添加一個大小為ξλ的約束力，從而使約束更加合理，ξ是人為定義的松弛參數常量，考慮影響的拉格朗日算子為

(9)

由此，可以得到考慮鄰域粒子密度約束修正情況下，且保證流體不可壓縮性條件的流體粒子的位移值為

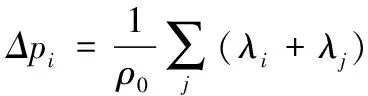
(10)

3 旋渦限制力

為實現海浪表面的逼真模擬，并體現海浪粒子運動實時性的特點，需要為海浪表面粒子添加旋渦限制力。本文在添加旋渦限制力階段采用的方法是渦度約束的方法[11]。不同于文獻[4]利用渦度約束函數來抵消因為方法本身產生的附加阻尼導致的原有渦旋的耗散，本文通過討論選用合理化調節系數，通過渦度約束函數產生旋渦控制力調節流體粒子系統速度場，從而達到逼真模擬海浪的目地。

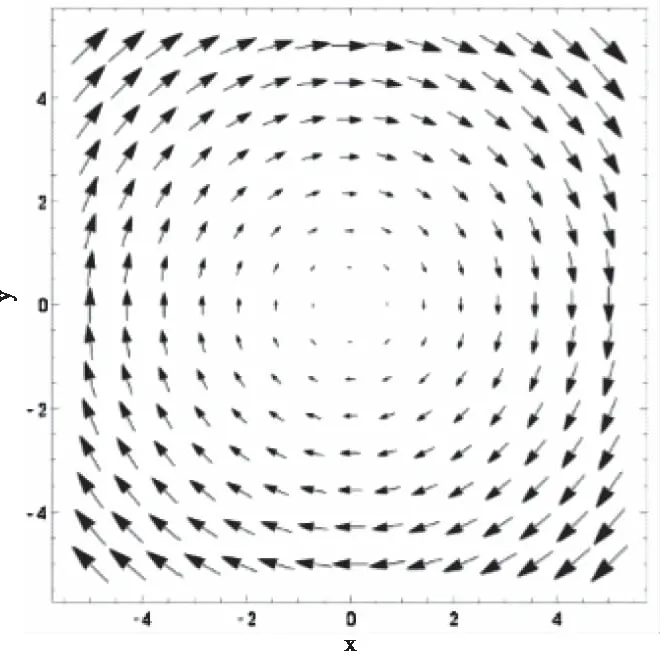
圖2 一個簡單向量的旋度場

3.1 Curl運算

在進行流體粒子渦度計算的時候，采用了Curl運算。向量分析中，旋度(Curl)是一個向量算子，表示在三維歐幾里得空間中的向量場的無窮小量旋轉，在向量場每個點上，點的旋度表示為一個向量，稱為旋度向量。這個向量的特征刻畫了在這個點上的旋轉。

在不同的坐標系下，向量場的旋度有不同的表達方式。PBF流體模型中采用的是流體粒子三維直角坐標系，所以三維直角坐標系中展開Curl運算。

設向量場A為

A(x，y，z)=Ax(x，y，z)i+Ay(x，y，z)j+Az(x，y，z)k

(11)

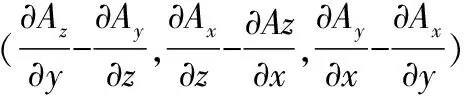
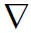
(12)

采用向量積的行列式記號形式可表示為：

(13)

3.2 渦度約束

渦度約束[12]的方法需要首先對于每一個流體粒子i采用Curl運算計算其渦度ωi：

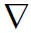
(14)

式中，mj為流體粒子的質量，ρj為流體粒子的密度，vi流體粒子的速度，vj為粒子i的鄰域粒子的速度。采用粒子i與鄰域粒子的速度差與梯度核函數進行叉乘，得到Curl運算的結果。

得到流體粒子的渦度ωi后，需計算流體粒子的位置矢量N：

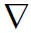
(15)

(16)

將計算所得位置矢量與已得渦度進行叉乘，得到流體粒子的旋渦控制力F：

(17)

最后，根據由旋渦控制力所求得的加速度，在時間步長內更新流體粒子的速度。在調節系數ε的控制下，旋渦控制力大小的不一致產生不同程度的流體粒子表面的起伏，從而實現逼真地模擬海浪。

4 結果與討論

4.1 實驗結果

實驗平臺是Intel(R)Core(TM)i5-7300HQ CPU 2.50 GHZ，主存16GB，GPU為NVIDIAGeForceGTX 1050 Ti，顯卡內存為4GB，開發環境VisualStudio 2015，采用OpenGL作為圖形的編程接口。

圖3顯示了粒子系統的初始形態，流體粒子數為12000，調節系數選定為0，即不添加旋渦控制力時流體粒子的潰堤模型。從圖中可以看出，粒子模型表面平整，無渦旋痕跡，較為光滑，是一種靜水中水面的模擬。但切合航海實際，大多數情況下海面不會是平靜的，在風流、浪涌的作用下，海面會產生浪花等不規則運動。所以添加旋渦限制力來模擬海面是必要地。

圖3 無添加旋渦限制力的流體粒子模型

圖4顯示了當調節系數選定為1.0時的流體粒子模型。此時隨著旋渦控制力的加入，流體模型表層粒子產生渦旋效果，渦旋與渦旋的邊界相疊加從而產生類似于波峰波谷的變化。

圖4 調節系數1.0下的流體粒子模型

隨著調節系數的不斷加大，流體粒子的運動劇烈程度逐漸加大。圖5為調節系數2.0下的流體粒子模型。與調節系數1.0下的粒子模型不同的是，當系數加大至2.0時，可以清楚地看到在模型的上方有部分粒子飛濺，同時整個模型的運動程度相比較系數1.0下更為劇烈。從航海實際來看，劇烈的海浪運動常常帶有翻卷、破碎飛濺等細節特征。當調節系數選取合適時，飛濺的粒子能恰好的模擬出海浪運動產生浪花飛濺等特效。

圖5 調節系數2.0下的流體粒子模型

4.2 比較分析

從實驗結果可以看出，流體粒子系統的運動劇烈程度隨著調節系數的增大而變得更加劇烈，但是海浪模擬的真實感不會隨著系數的增大而變得更為真實。當系數增大到一定程度時，流體粒子的旋向加速度會使其旋向速度過大，從而導致流體粒子發生橫向漂移。此時，流體粒子的運動已不符合自然物理規律，無法真實地模擬海浪運動。

表2給出了在不同調節系數下海浪運動的模擬效果。當調節系數選取在0～0.9之間時，流體粒子模型的渦旋程度只能模擬出原有流體粒子渦旋的耗散；當系數選取在1.0～2.9之間時，伴隨著所選取系數的增大，海面的波動程度不斷加深；系數選取在3.0～3.9之間時，整個流體粒子系統演變為一個大渦旋的旋轉運動，此時已無法真實地模擬海浪運動；當系數的選取大于4.0時，流體粒子系統發散。

表2 不同調節系數下的模擬效果

通過綜合比較分析，當調節系數取值在1.0～3.0之間，可以較好地模擬海浪運動。

5 結語

本文主要討論海浪真實感模擬問題。利用基于位置的動力學框架下的PBF方法進行流體粒子建模，再利用渦度約束的方法豐富流體表面細節。實驗結果表明，本文提出的合理化系數渦度約束方法能有效的模擬海浪表面的翻卷與破碎，提高了海面模擬的真實感。但對于流體表面重建與繪制以及調節系數的最優化選擇還需要做進一步的研究，從而繼續提升模擬的真實感。