雙凸極永磁電動機的建模及其系統仿真

楊天宇，張廣明

(南京工業大學電氣工程與控制科學學院，江蘇 南京 211816)

1 引言

20世紀90年代，美國Wisconsin大學的Thomas A.Lipo教授提出了雙凸極永磁電動機(Doubly Salient Permanent Magnet Motor，DSPM)[1]。DSPM結構簡單、成本較低、魯棒性強、功率密度和工作效率較高，在電動汽車、風力發電、航空航天等領域的應用日益廣泛。

DSPM的建模需要在推導電機數學模型的基礎上，確定電樞繞組的靜態特性(自感與磁鏈)。靜態特性的計算有三種方法：解析法、等效磁路法和有限元法。

解析法通過計算分段線性或非線性數學解析式，表示靜態特性隨轉子位置和電樞電流變化的情況[2]，缺點是無法同時具備模型精度高和數據處理簡便兩種優勢。等效磁路法通過求解等效磁路方程，考慮電樞反應對靜態特性的影響[3]，缺點是等效磁路的構建較為繁瑣。有限元法利用計算機有限元分析技術，根據電機結構和磁路特征計算靜態特性[4]，精度高且計算簡便，也沒有解析法和等效磁路法的固有缺陷。

關于DSPM建模的研究，目前大多局限在靜態特性的分析上。在仿真模型和系統構建方面的研究則較少，它們正是運用三相六狀態控制[5]和三相九狀態控制[6]等復雜控制策略的前提。

對此，本文建立了DSPM的仿真模型，構造了它的雙閉環系統。使用標準角度控制策略[7]進行了系統仿真，仿真結果驗證了電機建模和系統構造方法的有效性。

2 雙凸極永磁電動機建模

2.1 數學模型推導

在結構上，定轉子均為凸極結構的DSPM屬于變磁阻類型電機，工作時遵循磁阻最小原理，即磁鏈沿磁阻最小的磁路閉合[8]。特別處在于，DSPM在定子上安裝有用于勵磁的永磁體，在數學模型上與普通磁阻類型電機有顯著區別。

根據DSPM的磁路特征、電路特征、能量轉換原理和動力學原理，推導涵蓋磁鏈方程、電壓方程、轉矩方程和運動方程的數學模型。

2.1.1 磁鏈方程

由磁路特征，得到各相繞組磁鏈方程

(1)

式中：ψa，ψb，ψc為各相繞組的磁鏈；ψra，ψrb，ψrc為各相繞組的電樞磁鏈分量；ψma，ψmb，ψmc為各相繞組的永磁磁鏈分量；La，Lb，Lc為各相繞組的自感；Lab=Lba，Lac=Lca，Lbc=Lcb為各相繞組之間的互感；ia，ib，ic為各相繞組的電樞電流。

2.1.2 電壓方程

由電路特征，得到各相繞組電壓方程

(2)

式中：ua，ub，uc為各相繞組的端電壓；Ra，Rb，Rc為各相繞組的電阻。

將磁鏈方程代入電壓方程，同時因繞組間互感對計算的影響很小而將其忽略，得到各相繞組近似電壓方程

(3)

式中：θ為轉子位置角；ω為轉子角速度。

2.1.3 轉矩方程

根據機電能量轉換原理，同時忽略繞組間互感引起的較小磁阻轉矩分量，得到轉矩方程

Te=Tea+Teb+Tec

=Tra+Tma+Trb+Tmb+Trc+Tmc

(4)

式中：Te為電磁轉矩；Tea，Teb，Tec為各相輸出的有效電磁轉矩；Tra，Trb，Trc為各相自感磁阻轉矩；Tma，Tmb，Tmc為各相永磁轉矩。

2.1.4 運動方程

根據剛體定軸轉動的動力學原理，得到運動方程

(5)

式中：Tl為負載轉矩；J為電機轉子的轉動慣量；D為系統的阻尼系數。

2.2 靜態特性計算

三相DSPM定、轉子級數一般配置為6/4極和12/8極這兩種結構。其中，12/8極DSPM擁有更高的功率密度，且軛部磁路長度和繞組端部長度較短，磁路中的鐵損低、電樞中的銅耗低[9]。

DSPM中的永磁體按嵌入方式分為切向磁鋼和徑向磁鋼。內置徑向磁鋼相比普通切向磁鋼的優點是電機外部基本沒有漏磁場。

綜合上述分析，選擇了12/8極內置徑向磁鋼的DSPM作為建模對象，其結構參數如表1所示，截面圖如圖1所示。

表1 DSPM結構參數

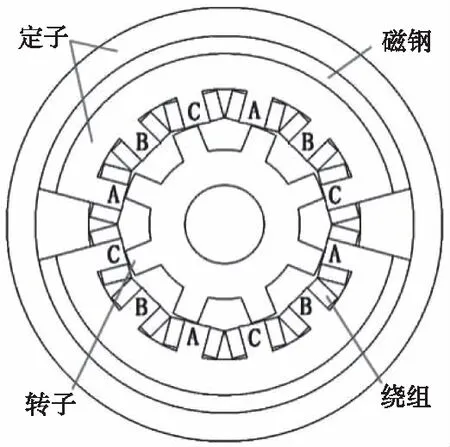
圖1 DSPM截面圖

運行方面，該DSPM的額定功率為550W，額定轉矩為3.5Nm，額定轉速為1500r/min，額定相電壓為60V。

DSPM的靜態特性包括各相電樞繞組的自感(忽略互感)和磁鏈，它們是轉子位置角和電樞電流的函數。研究表明，自感和磁鏈主要由永磁體提供，電樞反應對其影響很小[10]，故可近似表示為轉子位置角的一元函數。

在Ansys Maxwell軟件中，對DSPM進行2D瞬態場有限元分析。仿真得到了空載(無電樞電流)時各相電樞繞組的自感和磁鏈與轉子位置角(電角度)的對應關系，繼而繪制相應的關系曲線。曲線中轉子位置角的范圍為360°電角度(45°機械角度)，且0°時的轉子位置為圖1中的轉子位置。DSPM各相電樞繞組自感和磁鏈曲線如圖2和圖3所示。

圖2 DSPM各相電樞繞組自感曲線

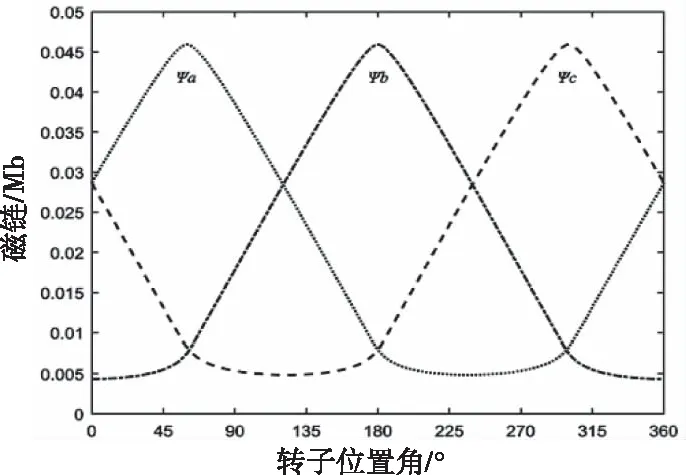
圖3 DSPM各相電樞繞組磁鏈曲線

根據曲線，DSPM各相電樞繞組的自感和磁鏈與轉子位置角呈現出明顯的非線性特征。

各相電樞繞組自感曲線呈馬鞍狀，當轉子極與定子極完全重合時，鐵心趨于飽和，磁阻增大，此時的自感值略小于半重合時的情況。

各相電樞繞組磁鏈曲線呈單峰狀，隨著轉子極與定子極重合程度的加深，磁鏈值逐漸增大。

2.3 仿真模型建立

利用DSPM數學模型方程和靜態特性數據，在Matlab/Simulink仿真環境中建立它的仿真模型。為計算各相電樞電流和電磁轉矩，根據電機數學模型，導入有限元分析所得的自感和磁鏈數據，并使用數值微分方法計算它們關于轉子位置角的偏導數。偏導數取值為自感和磁鏈數據關于轉子位置角的差商。

使用模塊庫中的Lookup Table模塊實現對自感、磁鏈和上述偏導數的插值。插值后自感和磁鏈曲線亦如圖2和圖3所示，自感和磁鏈對于轉子位置角的偏導數曲線則如圖4和圖5所示。

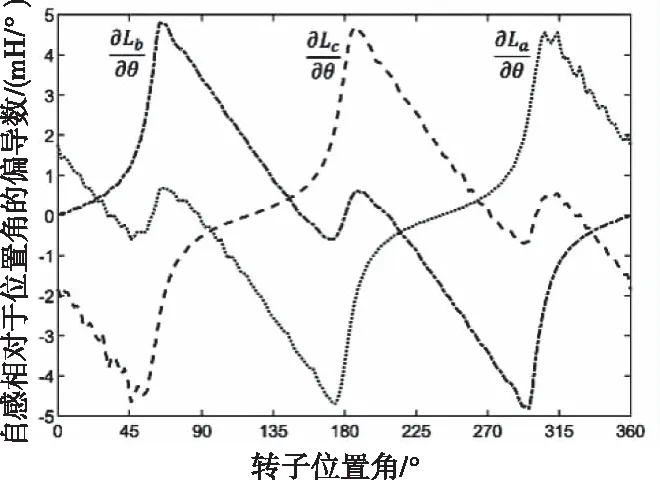
圖4 DSPM各相電樞繞組曲線

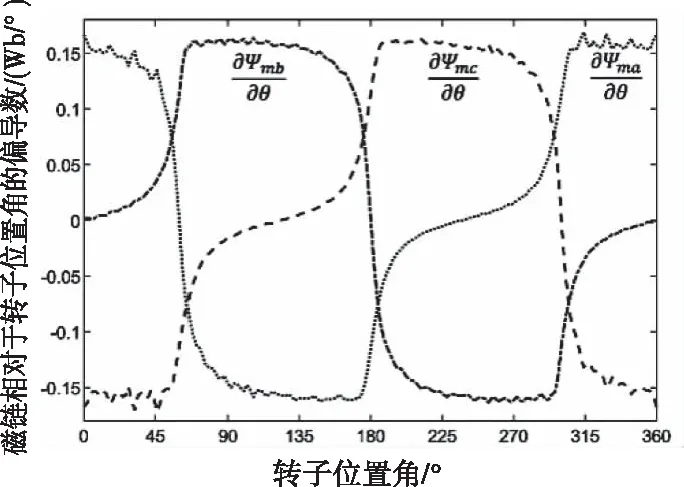
圖5 DSPM各相電樞繞組曲線

各相電樞繞組模塊根據電機數學模型和靜態特性數據搭建而成。其中有插值模塊以及表示正極和中性點的兩個物理建模連接(PMC)端口。同時，轉子位置信號為輸入信號，端電壓、相電流和相轉矩信號為輸出信號。

模塊內部計算過程如下：首先電壓測量模塊測量出端電壓；然后插值模塊根據處理后的轉子位置角，計算自感、磁鏈以及它們關于轉子位置角的偏導數；接著將端電壓代入電壓方程，計算相電流；再將相電流代入轉矩方程，計算相轉矩；最后通過信號輸出接口輸出端電壓、相電流和相轉矩。

A相電樞繞組模塊如圖6所示，其它相的電樞繞組模塊與A相類似。其中，電樞繞組的電阻R取值為0.28Ω。

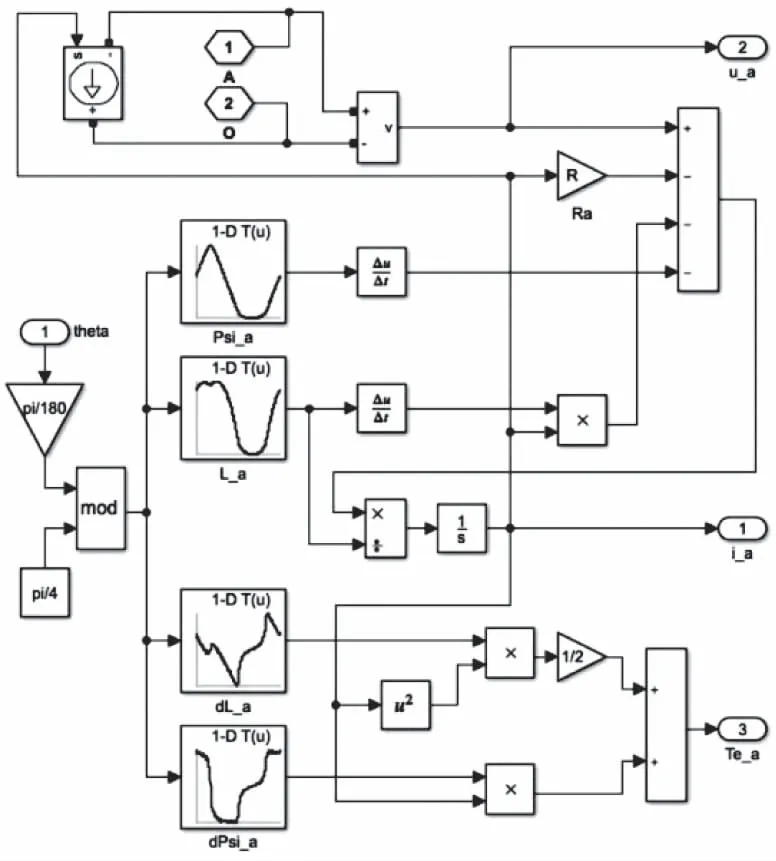
圖6 DSPM的A相電樞繞組模塊

DSPM的運動方程仿真模型如圖7所示。其中有一個表示電磁轉矩的信號輸入端口，以及兩個表示轉子轉速和位置角的輸出端口。根據實際情況，轉子的轉動慣量J取值為0.002kg·m2，系統的阻尼系數D取值為0.001N·m·s。

圖7 DSPM的運動方程模塊

上述各相繞組和運動方程模塊共同構成了DSPM的仿真模型。該模型如圖9中的DSPM模塊所示，其輸入為三相電樞繞組及其中性點的物理建模連接端口，輸出為三相電樞繞組的相電壓、相電流，轉子的位置角、轉速，以及電機的電磁轉矩。

3 雙凸極永磁電動機系統仿真

3.1 系統模塊化構造

DSPM系統框圖如圖8所示。該系統的控制方式為雙閉環控制。其中外環為轉速環，使用PI控制，內環為電流環，使用滯環控制。

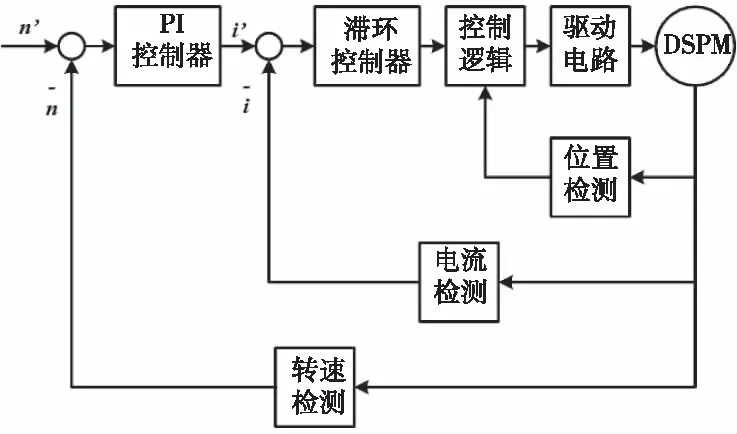
圖8 DSPM系統框圖

同時，DSPM是方波驅動型電機，采用標準角度控制策略，即在電樞繞組磁鏈的上升區間和下降區間內分別通入正負電流，在磁鏈接近為零的區間內不通電[7]。系統根據此策略，將檢測的轉子位置轉換為驅動電路中開關管的控制邏輯。

在Matlab/Simulink仿真環境中建立DSPM系統。按照模塊化的構造思想，將系統劃分為控制、驅動和DSPM三個主要模塊，各模塊便于集成和擴展。系統仿真結構圖如圖9所示。

圖9 DSPM系統仿真結構圖

3.1.1 DSPM模塊

DSPM模塊如圖10所示，它建立了DSPM精確仿真模型，其中包括各相繞組和運動方程子模塊。同時將各相電流、轉子轉速和位置角信號反饋至控制模塊。

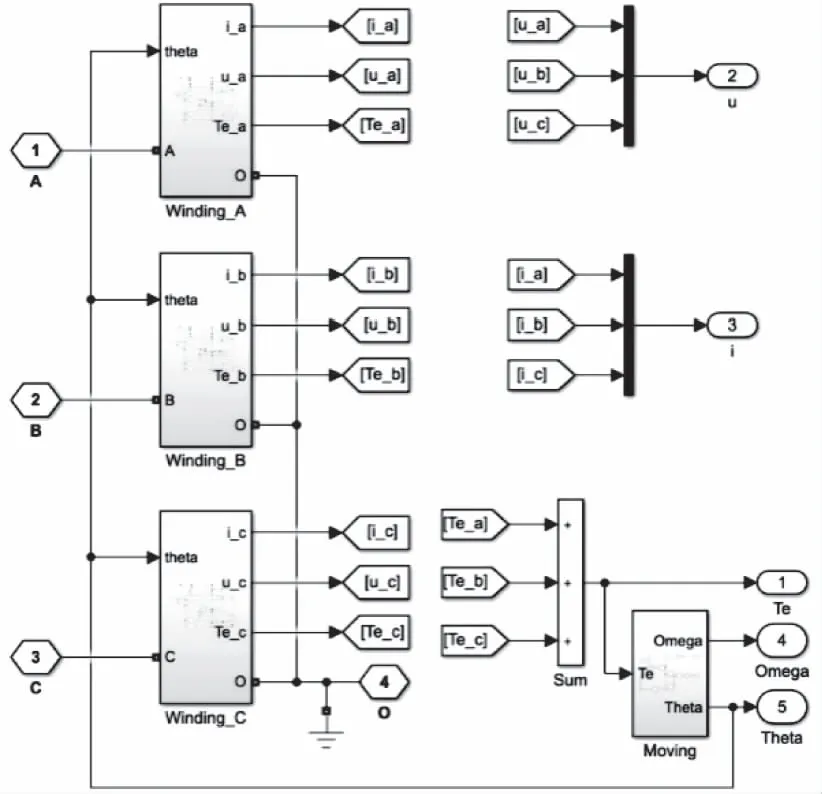
圖10 DSPM模塊結構圖

3.1.2 驅動模塊

驅動模塊如圖11所示，它構造了三相橋式逆變電路，其直流側電壓為120V，使用分裂電容均壓，門極驅動信號由輸入端發送至各功率晶體管，驅動電壓由輸出端提供至DSPM模塊。

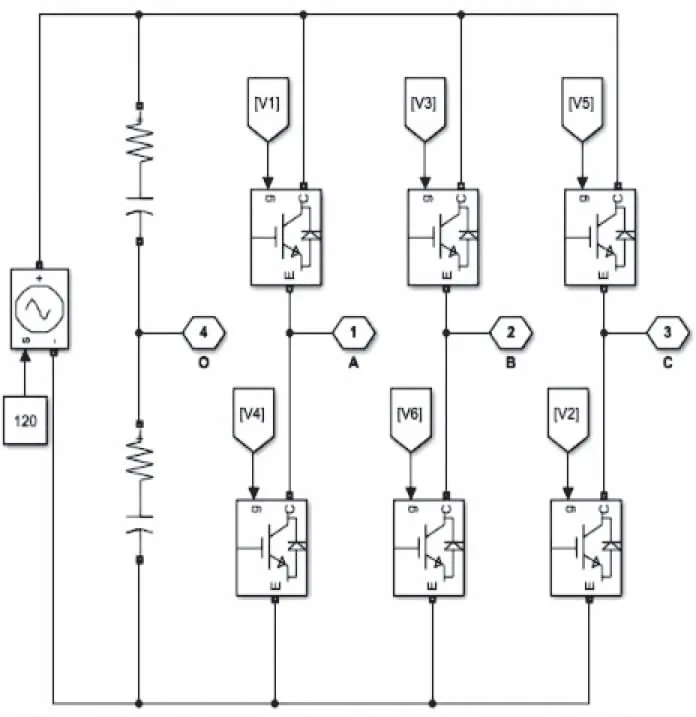
圖11 驅動模塊結構圖

3.1.3 控制模塊

控制模塊接收DSPM的反饋信號，生成驅動信號傳遞至驅動模塊，模塊內部分為三個部分。

雙閉環控制部分如圖12所示，該部分接收轉速和電流信號，經PI和滯環控制器，輸出各相PWM信號以及與參考電流同號的方向信號。方向信號為正1表示電動，為負1表示制動。PI控制器中Kp=0.064，Ki=0.8。為防止出現過流現象，參考電流限幅在±60A區間。

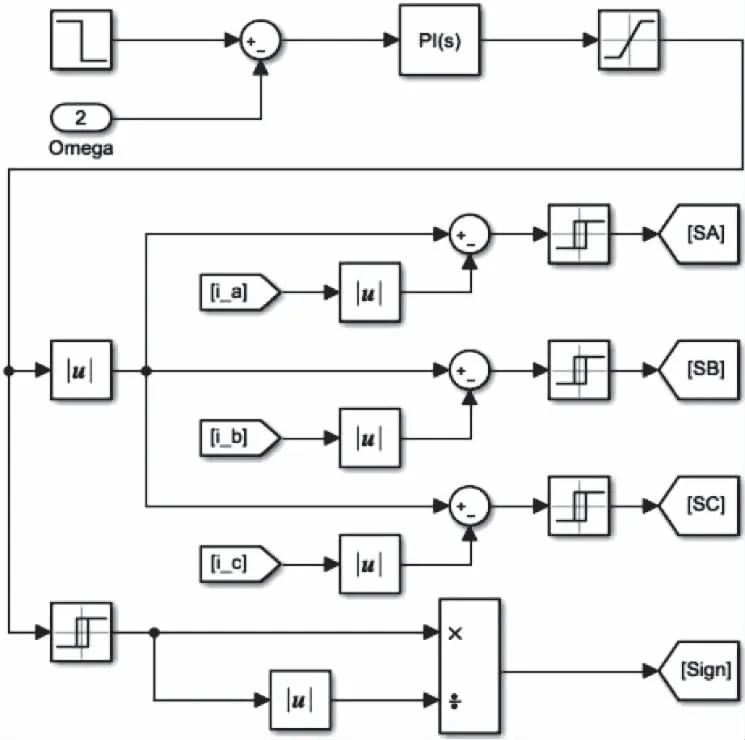
圖12 雙閉環控制部分模塊圖

標準角度控制部分如圖13所示，該部分接收轉子位置信號，根據標準角度控制策略，輸出驅動電路中開關管的導通信號。

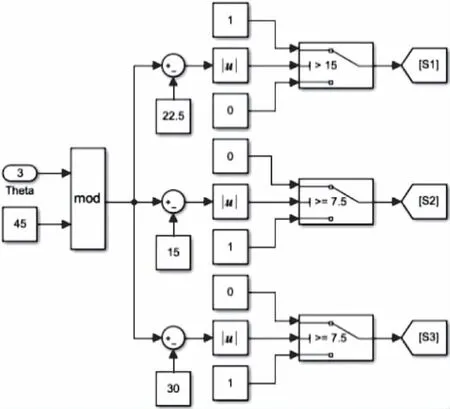
圖13 標準角度控制部分模塊圖

驅動信號輸出部分如圖14所示，該部分將轉向信號、各相PWM信號和開關管導通信號轉化為開關管驅動信號。

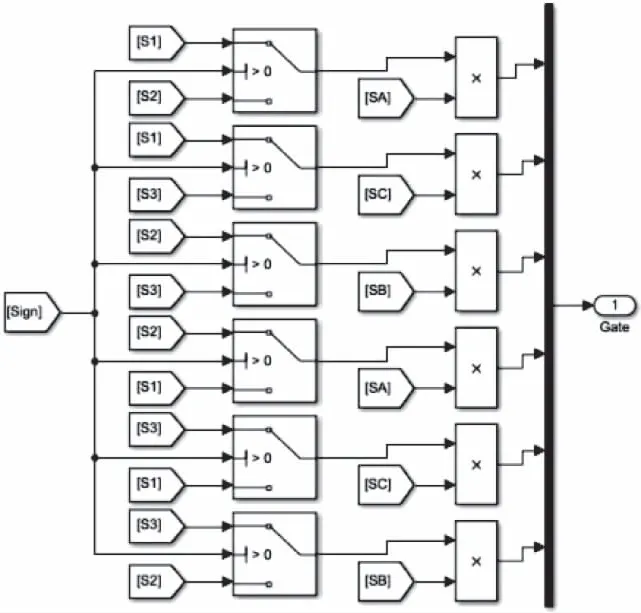
圖14 驅動信號輸出部分模塊圖

各轉子位置下，DSPM電動和制動運行時開關管的標準角度控制策略如表2所示。

表2 標準角度控制策略

3.2 系統仿真分析

對DSPM系統進行仿真，將其運行劃分為三個運行階段。各階段的時間、參考轉速和負載轉矩如表3所示。

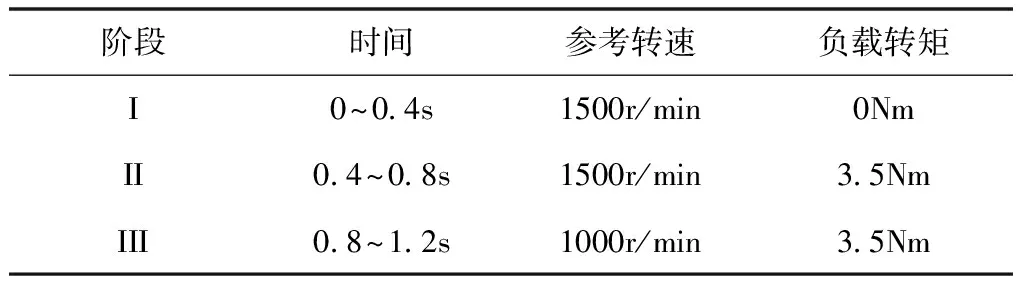
表3 DSPM各階段運行狀態

經過仿真，DSPM的實際轉速、A相電流、電磁轉矩波形如圖15所示。

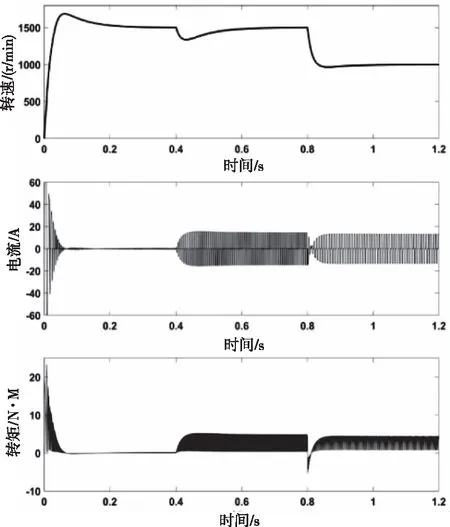
圖15 實際轉速、A相電流、電磁轉矩波形圖

三個階段中，電機實際轉速均較快地達到了準確的參考轉速。階段I中，電機空載起動，起動電流被限幅至±60A，隨后電流和轉矩衰減至穩定。階段II和階段III中，電機負載運行，且前者的電流和轉矩比后者大。綜合上述波形和分析，驗證了DSPM仿真系統整體的有效性。

額定狀態下DSPM三相電流波形如圖16所示。三相電流呈方波狀，任意時刻，兩相通正負電，另一相不通電，符合標準角度控制策略。同時由于各相自感大小的差異，使得換相時電流下降時間比上升時間長。

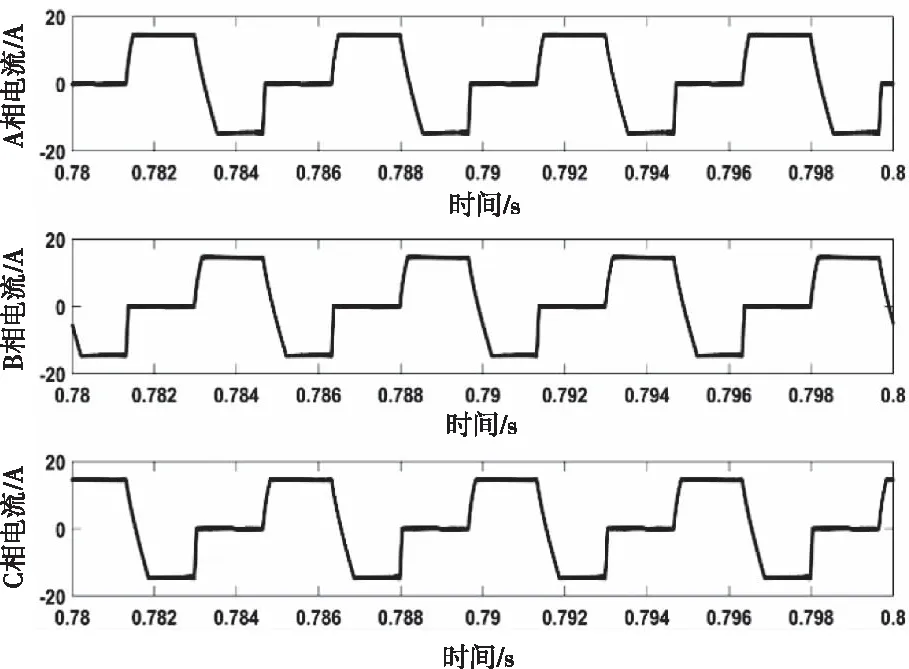
圖16 額定狀態下三相電流波形圖

額定狀態下DSPM三相轉矩與合成轉矩波形如圖17所示。各相轉矩和電流存在互相對應的關系，轉矩在對應繞組通電時產生，不通電時消失，換向時減小。合成轉矩由各相轉矩疊加而成。各相轉矩在換相時減小，形成合成轉矩典型的脈動狀波形。

圖17 額定狀態下三相轉矩與合成轉矩波形圖

綜合上述波形和分析，驗證了DSPM仿真模型建立的準確性。

4 結論

1)所分析12/8極內置徑向磁鋼的DSPM具有高功率密度、低鐵損、低銅耗的優點；

2)使用有限元法計算電機靜態特性，代入推導的數學模型方程，建立了DSPM仿真模型，此方法精度高且通用性強；

3)構造了DSPM完整的雙閉環系統，并仿真驗證了系統的有效性。該系統模塊化程度高且實用性強，便于集成和擴展，為研究復雜控制策略和提升控制性能提供基礎。