基于貝葉斯網的高維數據隱藏模式挖掘

陳傳毅，戴衛軍

(澳門城市大學，澳門 999078)

1 引言

高維數據就是指多維數據，是一維數據或者能夠寫成表達式的二維數據，而高維數據同樣可以類推，不過在維數較高時，很難直觀地表示，因此目前高維數據挖掘是重點研究對象。高維數據挖掘是指在大量的數據內，找出事先未知、隱含的，同時有用知識的一項任務[1]。是計算技術研究中一個非常具有價值的新領域，主要融合了統計學、機器學習、人工智能以及數據庫等多個領域的技術以及理論，成為數據庫領域以及國際信息的最新研究方向之一，受到工業界以及學術界的廣泛關注[2]。

文獻[3]采用無線傳輸技術，對異常數據進行降噪處理，結合FFD技術完成數據互通，根據FIFO挖掘思想，挖掘數據并設計挖掘流程，實現大規模高維數據挖掘算法。該方法的數據挖掘可靠性強。文獻[4]運用分段向量量化編碼技術，分析云數據空間存儲結構，根據閉頻繁項集檢測方法，信息融合處理云數據并提關聯規則特征，結合尺度分解方法，降維處理云數據，采用模糊聚類方法，對云數據進行分類挖掘。該方法數據挖掘的聚類性能較好。當前高維數據隱藏模式挖掘能夠利用降維把數據從高維降低至低維，通過增量方法以及并行方法來提升計算性能。而當前高維數據隱藏模式挖掘精度較低，挖掘執行時間較長，且挖掘過程工作量較大，挖掘過程較為復雜，很難滿足實際需求。

針對上述問題，本文提出一種基于貝葉斯網的高維數據隱藏模式挖掘方法，通過有向無環圖像以及概率表所構成貝葉斯網絡，利用信號處理的方法來對數據信息進行特征提取，對子空間降維處理，采用自適應級聯濾波完成數據的降噪，將多通道聲的傳感信息數據完成自適應進行波束構成，聚焦數據，從而完成高維數據的隱藏挖掘。

2 貝葉斯網絡理論

貝葉斯網絡構成，具體步驟有以下兩個部分：

第一步：有向無環圖像(DAG)，其中所有節點都表示一個數據變量Xi，Pai表示Xi父節點集合。

第二步：另外一個條件的概率表(CPT)，在表內所有元素代表數據變量Xi條件的概率密度p(Xi，Pai)。

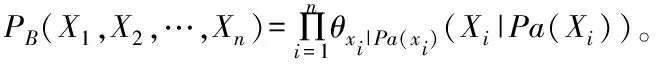
貝葉斯網絡主要是針對概率推理與圖理論所建立的模型，此模型具體表示為有向無環圖，是利用節點與弧進行構成的，在其中節點表示變量的關系，具體表示為證據或者事件，在兩個節點之間，弧表示時間之間的關聯性，是作為單項式的，而進行反饋環路并不存在[6]。根據此特性，就能夠對父子節點間的關系或者是相連節點之間的互相關聯概率進行確認。

貝葉斯網絡在應用于條件概率時，假如某些已經發生的證據事件E是針對假設性H的，那么H與E二者則同時具有的概率P(H，E)能夠被定義成P(H，E)=P(H)P(E|H)。

具體網絡結構的表達節點之間具有條件獨立的聯系，且存在3種局部構造[7]，具體如下所示：

順連圖像：

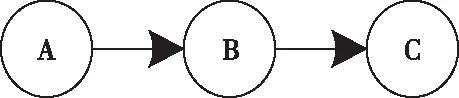
圖1 貝葉斯網絡順連結構示意圖

具體公式為：

P(A，B，C)=P(C|B)P(B|A)P(A)

(1)

分連圖像：

圖2 貝葉斯網絡分連結構示意圖

具體公式為：

P(A，B，C)=P(C|B)P(A|B)P(B)

(2)

匯連圖像：

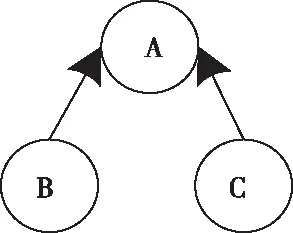
圖3 貝葉斯網絡匯連結構示意圖

具體公式為：

P(A，B，C)=P(B|C，A)P(C)P(A)

(3)

根據乘法定律的交換性質，假如H與E二者相關，則說明E就一定會與H有關系，基于此聯合概率代表公式為

P(H，E)=P(H)P(E|H)=P(E)P(H|E)

(4)

所以

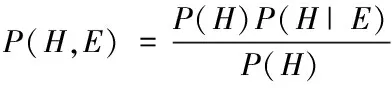
(5)

式(5)為葉貝斯公式，依據統計學角度，P(H)表示因假設H所引起的E產生條件概率，被稱為H對于E似然估計[8]。證明了H是在真實情況中E所產生的信度。P(H|E)是后驗的概率，如：E產生條件中H所出現概率。

貝葉斯網推斷的基本步驟是：首先選取一個概率密度的函數π(θ)，代表在獲取數據前某一個參數θ信念，將其稱為先驗的分布，對一個模型π(x|θ)進行選取，能夠反映出給定參數θ狀態中對于x信念，在獲取數據X1，X2，…，Xn之后，對信念進行更新，同時計算后驗的分布π(θ|X1，X2，…，Xn)，在后驗分布內獲取點的估計與區間的估計。

貝葉斯網絡可以提供一種便利的表示因果知識路徑，在其網絡中，節點是能夠作為“輸出節點”來對類符號的屬性進行表示，且能夠同時存在多個輸出節點，而對于分類過程所返回類標號的屬性分布概率，就可以對所有類概率完成預測[9]。具體主要來源不確定：

1)該方面的領域專家對于自己掌握的知識的不確定性。

2)在建模的領域自身中存在的不確定因素。

3)知識工程師的表示知識、試圖翻譯而造成的不確定因素。

4)對于知識本身準確性以及所獲取的知識方面，所具有不確定的因素。

通過概率方法完成不準確性步驟的推理，具體過程如下：

第一步：將待處理的問題域，進行抽象成一組隨機的變量集X=X1，X2，…，Xn。

第二步：將相關此問題的知識，代表成一個聯合概率的分布P(X)。

3 高維數據隱藏模式挖掘

3.1 數據挖掘框架分析

基于數據挖掘質量分析的系統框架結構圖像，具體如圖4所示。

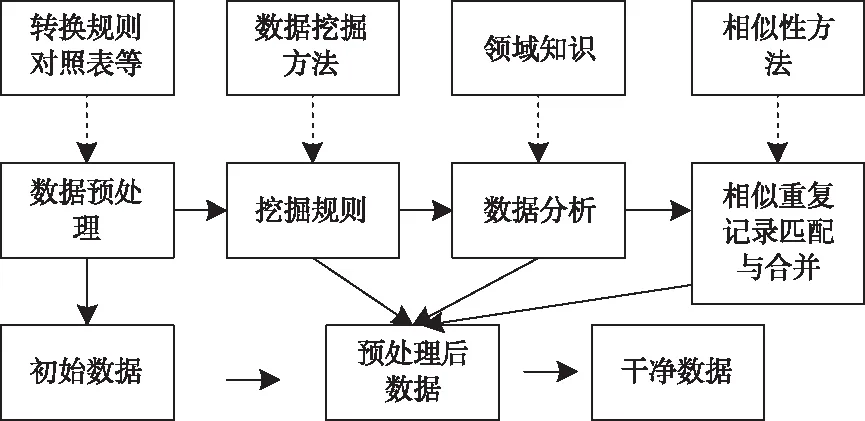
圖4 數據挖掘與質量的框架分析

數據挖掘的質量分析一般分成4步：

數據預處理：當轉換規則與對照表的指導下，來對初始數據進行元素化以及標準化的處理，構成預處理之后的數據信息，而元素化就是解析地址等自由的格式化的文本數據信息[10]。

挖掘規則：該步驟是在預處理之后的數據上，選取數據的挖掘方法，隱藏挖掘規則等。

數據分析：利用挖掘出的規則對異常數據進行發現，同時進行對應的標記或者結合領域內知識完成修正。

類似重復的記錄匹配與合并：對相似對象識別，清除重復記錄與冗余字段，完成記錄合并。

3.2 降維處理與降噪處理

利用信號處理方法對數據信息進行特征提取，完成數據高維數據隱藏信息的挖掘。首先對高維數據進行子空間降維，利用貝葉斯網絡對高維數據縮小開銷計算，而相對于高維數據的時間序列x1，x2，…，xn，…，能夠將其設置成采樣數據時間的序列長度是N，而序列{Xi}時間的延遲是jτ，具體數據構造之間的自相關函數公式是

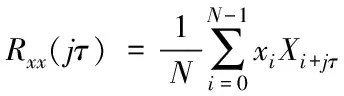
(6)

以此可以固定j，獲取高維數據特征的矢量子空間，具體的子空間函數公式是

Xq=UDXTRxx(jτ)

(7)

式(7)中：U表示正交函數，把上述奇異值(SVD)分解，D表示高維數據的子空間類間的平均距離大小排序，XT表示非零的特征值。經過以上的子空間降維，完成數據的維度降低。然后以此作為基礎，利用自適應級聯濾波完成數據的降噪[11]。

如果數據的挖掘背景噪聲內，具有Nx個正弦的信號，那么就說明所有的結構單元Hi(z)都是可變參數θ1i(k)，最后選取可以使系統輸出噪聲更小的，具體濾波器傳遞函數公式為

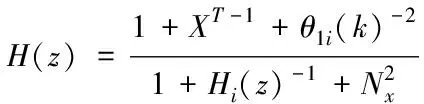
(8)

與簡化梯度的算法進行結合，利用級聯的Nv個陷波器將濾波函數改成

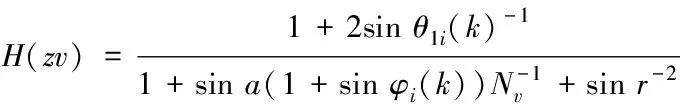
(9)

式(9)中：陷波器頻率的參數a與帶寬的參數r，φi(k)主要是作為第i級梯度的信號，在經過上述處理，就能夠完成對數據降噪，提升數據的挖掘精度。

3.3 數據隱藏模式挖掘

經過上述的降維處理與降噪濾波之后，能夠將多通道的傳感信息數據完成自適應的波束構成，然后利用提取特征的方式來對數據完成聚焦[12]，具體輸入高維數據的噪聲p(ek|uk)，方差與均值服從的分布公式為

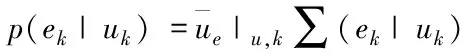
(10)

相對于多個已知的干擾線譜內的高維特征矢量，建立自適應的波束形成器公式為

xmin，j=min{H(z)(xmax，j-xmin，j)}

(11)

xmax，j=max{H(z)(xmax，j-xmin，j)}

(12)

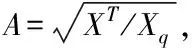
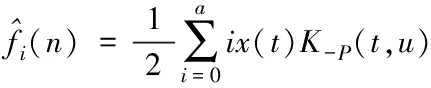
(13)

經過自適應的波束構成，其高維數據的矢量x(t)以及波束的聚焦核K-P(t，u)是作為基函數所展開的，具體構成新的映射公式為

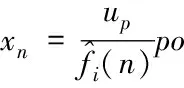
(14)

將up軸定義成po階段的Fourier域，則噪聲與干擾的情況，就能夠利用自適應的波束所形成，以此完成高維數據的隱藏挖掘。

4 實驗結果分析

為了驗證所提方法的有效性，在仿真為MATLABR2014的環境下，選擇浪潮XEON服務器，CPU主頻選擇2.4GHz，內存選擇4GB，軟件選擇Windows 2003，程序選擇Delphi7編寫進行實驗。在實驗中的6組數據集是T40.I30.D8000K，其項目數分別為5000、10000、15000、20000、25000，事務量分別為2000、4000、6000、8000、10000，通過IBM數據發生器構成，存在高維大數據集特征。分別采用文獻[3]方法、文獻[4]方法和所提方法對高維數據隱藏模式挖掘的執行時間進行對比，具體對比結果如圖5所示。

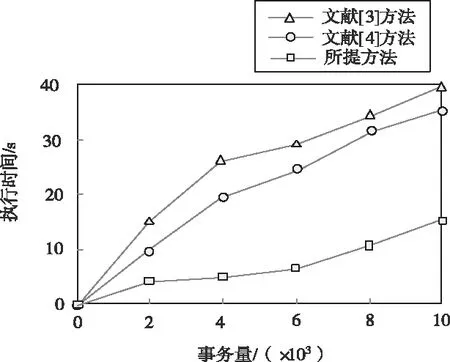
圖5 不同方法高維數據隱藏模式挖掘執行時間

分析圖5可知，隨著事務量的增加，不同方法的高維數據隱藏模式挖掘執行時間均增加。其中，文獻[3]方法的高維數據隱藏模式挖掘平均執行時間為28.8s，文獻[4]方法的高維數據隱藏模式挖掘平均執行時間為24.4s，而所提方法的高維數據隱藏模式挖掘平均執行時間為9s。由此可知，所提方法的高維數據隱藏模式挖掘執行時間較短，本文主要采用貝葉斯網絡確認父子節點間的關系或相連節點之間的互相關聯概率，從而有效縮短高維數據隱藏模式挖掘執行時間。

在此基礎上分別采用文獻[3]方法、文獻[4]方法與所提方法對高維數據隱藏模式挖掘工作量進行對比。minlen是評價高維數據隱藏模式挖掘過程工作量大小的指標。minlen越大，說明高維數據隱藏模式挖掘工作量越少，反之，minlen越小，說明高維數據隱藏模式挖掘工作量越多，如果minlen太小了，則交集的事務量增加明顯，導致高維數據隱藏模式挖掘執行時間較長，從而影響了整體的性能。具體對比結果如圖6所示。

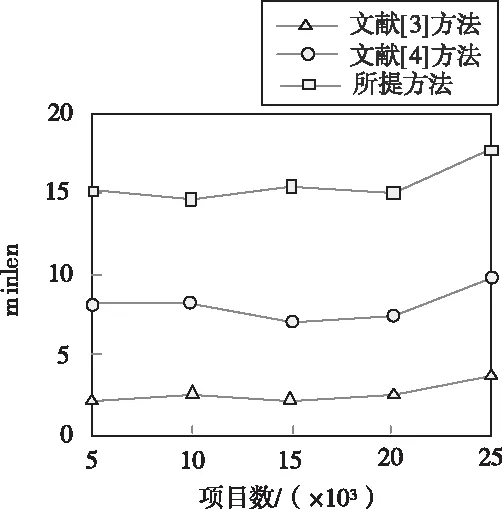
圖6 不同方法高維數據隱藏模式挖掘工作量

分析圖6可知，當項目數為25×103時，文獻[3]方法的minlen值最大為4，文獻[4]方法的minlen值最大為10，而所提方法的minlen值最大為17。由此可知，所提方法的高維數據隱藏模式挖掘工作量越少，挖掘過程較為簡單。

為了進一步驗證所提方法的精度，在同一條件下，選取6組數據集，將所提方法與文獻[3]方法、文獻[4]方法進行對比，具體對比結果如圖7所示。

圖7 不同方法高維數據隱藏模式挖掘精度

通過圖7能夠看出，文獻[3]方法和文獻[4]方法的高維數據隱藏模式挖掘精度僅在70%左右，在實際應用時，經常會出現部分數據挖掘遺漏的情況。而所提方法的高維數據隱藏模式挖掘精度在90%左右，雖然同樣存在部分遺漏，但相對于文獻[3]方法和文獻[4]方法遺漏的數量較少，在實際應用效果較好。由此可以看出，所提方法的高維數據隱藏模式挖掘精度較高，本文主要利用自適應級聯濾波對高維數據降噪處理，有效提升數據的挖掘精度。

5 結束語

目前計算機技術各種類型數據收集工作量越來越大，致使數據庫的規模逐漸變大，數據維度也越來越高。而這些高維的數據中，僅有部分的數據是有用的，所以需要在其中進行挖掘，尋找出有用的數據進行利用。而當前數據挖掘方法，由于挖掘精度低，執行時間較長，且挖掘過程工作量較大，過程較為復雜，很難達到實際應用需求。本文提出一種基于貝葉斯網的高維數據隱藏模式挖掘方法，先闡述貝葉斯網絡的構成，通過貝葉斯網來計算高維數據，減少計算開銷，利用信號的方式來對數據特征信息提取，完成高維數據子空間信息的降維操作，采用自適應級聯濾波對高維數據進行降噪，最終把多通道聲傳感信息的數據完成自適應進行波束構成，聚焦數據，完成數據挖掘。實驗結果表明，所提方法能夠有效縮短高維數據隱藏模式挖掘執行時間，且數據挖掘精度，其挖掘過程工作量較小，挖掘過程較為簡單。