基于增量式學習的網絡攻擊檢測數學建模仿真

王成滿

(四川外國語大學重慶南方翻譯學院，重慶 401120)

1 引言

科學技術的迅速發展使社交網絡、交通運輸、通信運營等多個領域均形成著大量的數據，這些數據存在著許多對管理者的決策起助力價值的信息[1]。隨著數據規模的增長，數據挖掘方法已變成當今社會的重點研究項目之一。互聯網網絡規模的擴大令越來越多的系統遭受到黑客的入侵，網絡攻擊的手段日漸復雜，網絡安全問題越來越突出[2-3]。

為了保障網絡的安全運行，相關專家們展開了大量研究。文獻[4]提出了基于內網行為分析的網絡攻擊檢測數學模型，首先需要獲取網絡中的信息資源，其次對網絡中的行為異常風險要素進行分析，最后將信息的節點及資源獲取途徑當作要素，創建一個攻擊檢測模型，利用該模型實現對網絡攻擊的檢測。文獻[5]提出了基于流量和IP熵特性的DDoS攻擊檢測方法，構建M-ATS的網絡攻擊檢測數學模型，將博弈論(M-ATS)與馬爾可夫判決進程(MJP)攻擊模式挖掘算法進行了結合，通過M-ATS確定最佳網絡保護方法，利用MJP對未來發生的網絡攻擊進行預測，根據預測結果設計相應的保護方案，實現對網絡攻擊的檢測。文獻[6]提出了基于蟻群算法的網絡攻擊檢測數學模型，將蟻群收斂到的路徑當作網絡異常路徑，求解該異常路徑上各個節點的O-measure值，通過O-measure值來確定網絡攻擊所在位置，實現對網絡攻擊的檢測。

雖然當前研究取得一定進展，但是依然存在網絡攻擊檢測率較低、網絡攻擊誤報率較高以及檢測時效性較差等問題，并不適用當前的網絡攻擊檢測。因為網絡信息間拓撲關系不明確，所以在估算網絡信息的法向量及曲率時，需構建網絡信息間的拓撲關系，提出基于增量式學習的網絡攻擊檢測數學模型。

2 基于增量式學習的網絡攻擊檢測模型

2.1 網絡信息噪聲去除

由于網絡信息間不存在明確的拓撲關系，在估算網絡信息的法向量及曲率時，需要構建一個網絡信息之間的拓撲結構關系[7]。

假設網絡信息點pj的k鄰域點集是Nk(pi)構造關于pi的協方差矩陣

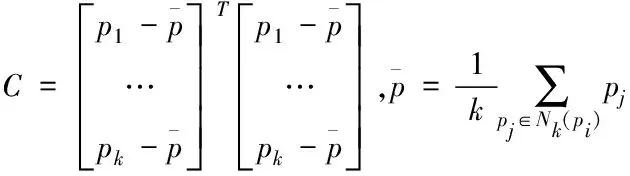
(1)

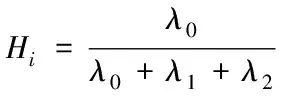
(2)

將式(2)得到的法矢方向調成相同的方向。

?pi∈P的k鄰域點集是qi∈Q(i=1，2，…，k)，已知pi處的平均曲率是Hi，那么信息點pi在k鄰域下的局部權值求解公式為

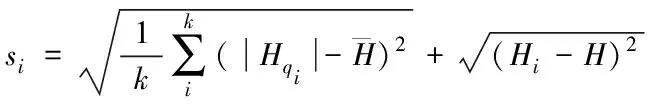
(3)

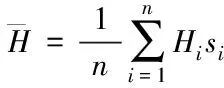
(4)

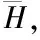
模糊C均值聚類算法將包含n個l維向量pi(pi1，…，pil)的集合P={p1，p2，…，pn}分成m個組O={o1，o2，…，om]，每個組和一個聚類中心相對應，求解每一個聚類組的聚類中心oj，(j=1，2，…，m)，致使目標函數J最小，目標函數J(U，O)的表達式如下

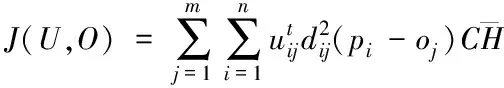
(5)

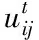
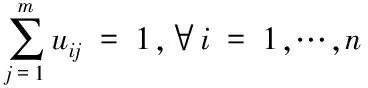
(6)

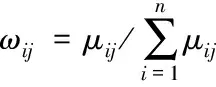
(7)

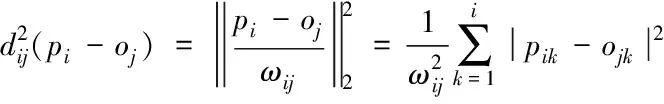
(8)

模糊權重系數使距離遠的向量uij對oj的影響變小，距離近的向量對oj的影響變大。這種控制方式有效地擴大了離群向量的特征[9]。特征保持權值求解方式如下

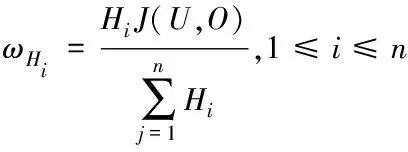
(9)

ωHi用于說明信息點pi的曲率對聚類的影響。

由于x，y，z在信息點附近的信息分布密度較大的情況下，信息點間的距離較近，信息點密度ρi較大，所以構建了一個密度影響權值因子

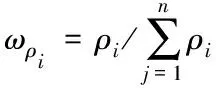
(10)

ωρi表示信息點pi的密度對聚類的影響。利用模糊C均值聚類的權重因子能夠獲得目標函數，利用該目標函數實現拓撲幾何學原理信息點的密度求解公式如下

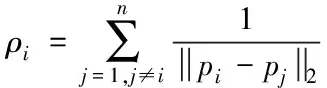
(11)

基于上述分析，構建一個網絡信息之間的拓撲結構關系，其表達式為

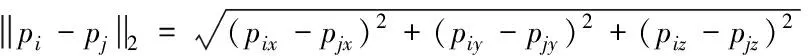
(12)

利用該拓撲結構關系即可實現對網絡信息的噪聲去除，其公式為

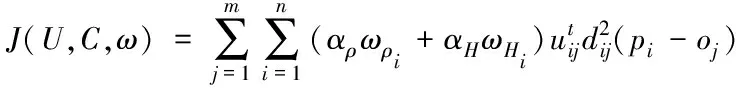
(13)

式中，αH表示特征保持系數，αρ表示密度影響系數，J(U，C，ω)為去噪后的網絡信息。

2.2 基于增量式學習的網絡攻擊檢測模型

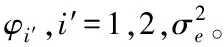
φi′=(X″TX″)-1X″TY

(14)

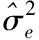
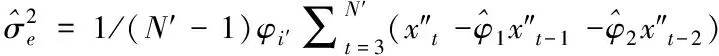
(15)

式(16)與式(17)為AR(2)的參數估計

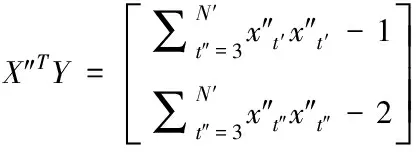
(16)

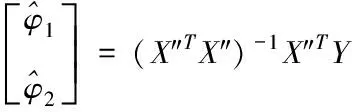
(17)

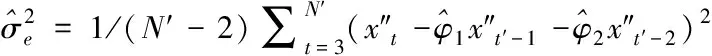
(18)

二階自回歸模型的參數X″TY由時間序列數據的線性估計得出。利用二階自回歸模型檢測移動網絡信息樣本et′

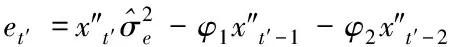
(19)

若et′是后移算子，那么

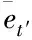
=x″t′-φ1Bx″t′-φ2B2x″t′

=(1-φ1B-φ2B2)

=φ(B)x″t′

(20)

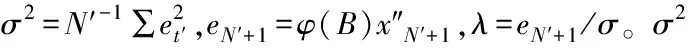
λ<-L′||λ>U

(21)

其中，L′和U是正數。

在進行網絡攻擊判定實現檢測的基礎上，假設離散型屬性連續化后的增量式學習網絡攻擊檢測信息矩陣如式(22)所示。

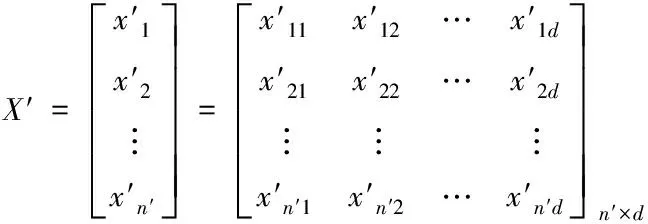
(22)

其中，n′表示去噪處理后數據集中樣本的數量，M表示去噪后數據狀態節點隊列，d表示樣本屬性數量。則均值標準差歸一化方法對數據集中每個屬性值做歸一化處理，歸一化求解公式如下

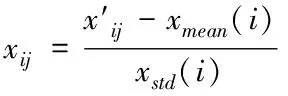
(23)

式(23)中，xmean(i)和xstd(i)分別表示第i列數據的平均值和標準差，xij表示歸一化處理后的屬性值。

對去噪處理后的樣本信息采用B-ISVM增量式學習算法[10]。利用該算法完成對網絡攻擊信息的歸一化處理。設X為增量式學習網絡攻擊檢測矩陣X′歸一化處理后得到的一個矩陣

(24)

將歸一化處理后的樣本信息作為一個滑動時間窗，設滑動時間窗的大小是N′+1，每次從時間窗中取出N′+1個樣本信息。

時間窗內的N′+1個信息樣本利用y1，y2，…yN+1來說明，利用前N′個信息樣本構建一個自回歸模型AR，判斷第N′+1個信息樣本是否存在異常。選取恰當的AR階數q′，時間窗口大小N′應該相對小一些，AR(q′)在擬合時間序列時，準確使用FPE衡量。時間窗口大小N′和階數q′的約束條件是0≤q′≤0.1N′，利用x″1，x″2，…，x″N′+1對二階自回歸模型AR(2)進行擬合，擬合后得到的基于增量式學習的網絡攻擊檢測模型x″t′為

x″t′=φ1x″t′-1+φ2x″t′-2+et′J(U，C，ω)+xij

(25)

最后，完成了對基于增量式學習的網絡攻擊檢測數學模型的構建。

3 仿真設計與結果分析

為了客觀評估實驗結果，實驗中采用網絡攻擊檢測率、網絡攻擊誤報率、網絡攻擊時效性、抗網絡攻擊性能四項評估指標來驗證本文所提方法的有效性。

3.1 實驗環境

假設網絡攻擊檢測率為

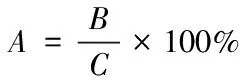
(26)

其中，A表示網絡攻擊檢測率，B表示被正確分類的網絡攻擊樣本數量，C表示實驗樣本集中網絡攻擊樣本的總量。

網絡攻擊誤報率的設定為

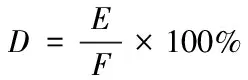
(27)

其中，D表示網絡攻擊誤報率，E表示被錯誤分類的正常樣本數量，F表示正常樣本的總量。

實驗環境：本次實驗在內存為2G，操作系統為Windows的計算機上進行，實驗測試平臺是Matlab7.0。

3.2 網絡攻擊檢測結果

實驗從KDDCUP 1999數據集中隨機選取實驗樣本，在對實驗樣本進行離散化后，形成的實驗樣本集如表1所示。

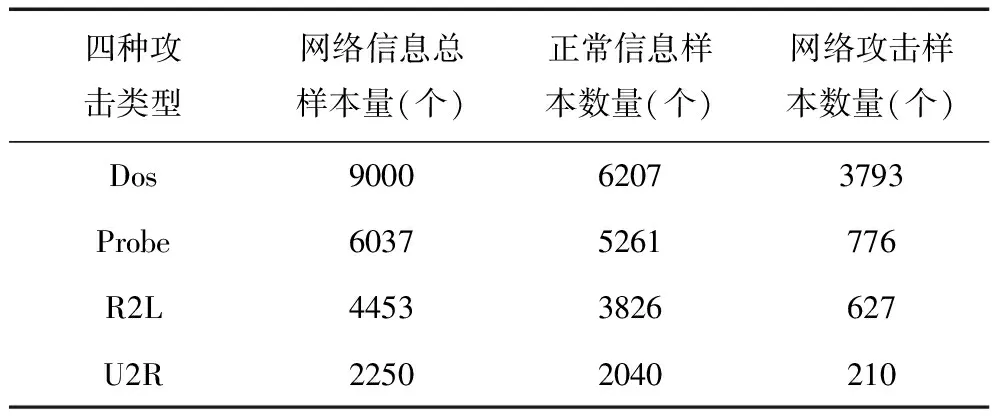
表1 網絡攻擊檢測實驗樣本集

數據集通常由正常和異常兩種信息構成，異常信息分為四種類型，分別是DoS、Probe、R2L和U2R。其中每一種異常信息均包含多個子類型。

為了描述方便，將本文所構建的檢測數學模型描述為A，基于行為分析的網絡攻擊檢測數學模型描述為B、基于流量和IP熵特性的DDoS攻擊檢測數學模型描述為C、基于蟻群算法的網絡攻擊檢測數學模型描述為D。四種網絡攻擊檢測數學模型的檢測結果，如表2所示。

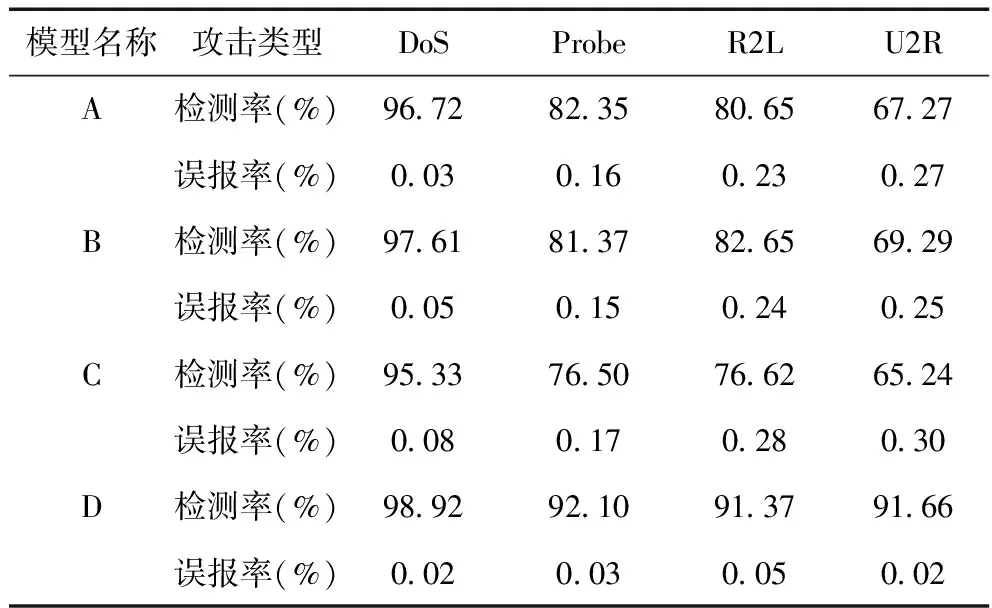
表2 網絡攻擊檢測結果

從表2可以看出，四種網絡攻擊檢測數學模型中，本文所構建模型的網絡攻擊檢測率是最高的，網絡攻擊誤報率是最低的，幾乎可以忽略不計，且可以檢測出絕大多數的網絡攻擊，這是由于所構建的數學模型在檢測網絡攻擊之前，對檢測數據進行了去噪處理，通過上述實驗數據可知，本文所構建數學模型適用于對檢測率和誤報率有較高要求的場合。

3.3 網絡攻擊時效性和抗網絡攻擊性能結果

3.3.1 網絡攻擊時效性對比

為了驗證本文所構建的檢測數學模型的時效性，將檢測模型A與B、C和D三種數學模型進行了對比分析。四種數學模型的網絡攻擊檢測時效性對比結果如表3所示。

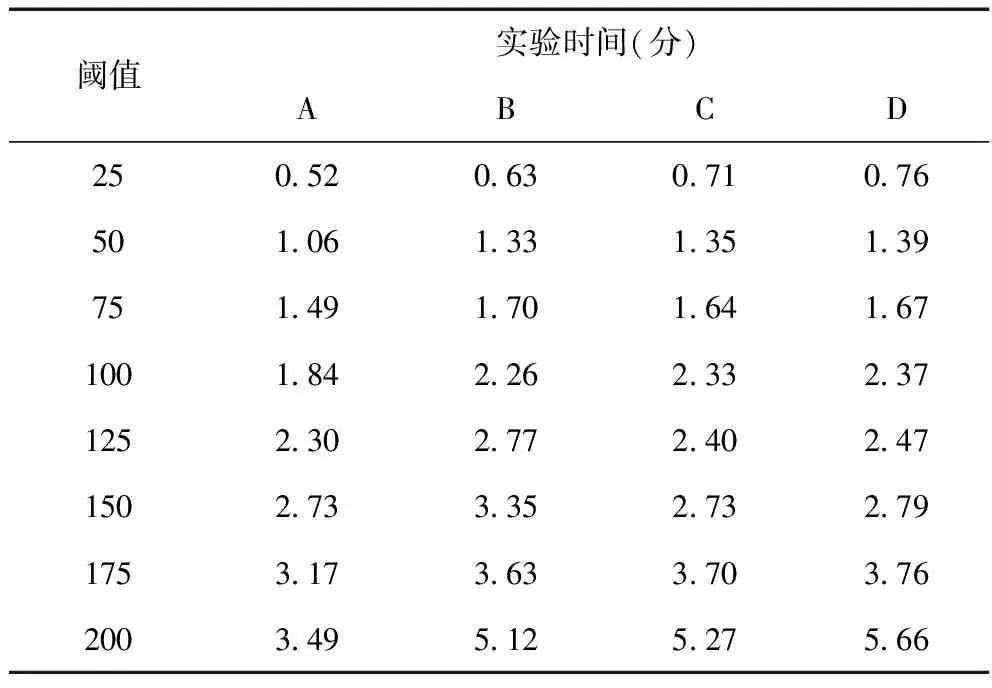
表3 時效性對比

從表3可以看出，四種網絡攻擊檢測數學模型中，A數學模型的時效性最高，其次是B數學模型，D數學模型的時效性是四種數學模型中最差的。以閾值25和閾值100為例，當閾值為25時，A模型實現網絡攻擊檢測所需的時間要比B、C、D三種模型分別縮短17.5%、26.8%、31.58%；當閾值為100時，A模型實現網絡攻擊檢測所需的時間要比B、C、D三種模型分別縮短18.58%、21.03%、22.36%，通過上述實驗數據可知，所構建數學模型A較B模型、C模型和D模型得到了極大的改進，采用本文所構建數學模型A能夠高效實現對網絡攻擊的檢測。

3.3.2 網絡攻擊時效性對比

為了驗證本文所構建網絡攻擊數學模型的抗攻擊能力，將本文所構建模型A與B、C和D三種數學模型的抗攻擊能力進行了對比。對比結果如圖1所示，其中橫坐標為網絡攻擊數量，單位是個，縱坐標為抗網絡攻擊性能，單位是百分比(%)。

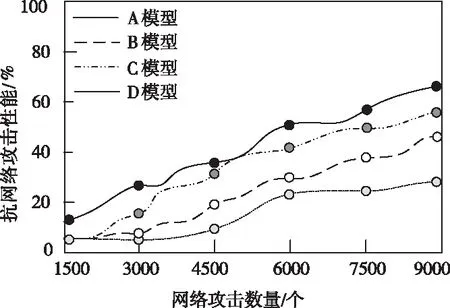
圖1 四種數學模型的抗網絡攻擊性能對比圖

從圖1可以看出，在相同網絡攻擊數量的情況下，四種模型中所構建模型A的抗攻擊性能最高，其次是模型C，模型D的抗攻擊性能最低。通過上述實驗數據可知，采用所構建模型A可以在準確檢測網絡攻擊的前提下，提高網絡的抗攻擊能力。

綜上所述，本文所構建的數學模型A具有高檢測率、低誤報率、高時效性、高抗攻擊能力的特點。采用本文所構建的數學模型能夠在高時效、高檢測率、高抗攻擊能力的情況下實現對網絡攻擊的檢測，且誤報率較低。表明本文所構建的模型具有較好的檢測性能。

4 結論

針對現有網絡攻擊檢測數學模型存在的網絡攻擊檢測率較低、網絡攻擊誤報率較高、檢測時效性較差等問題，構建了基于增量式學習的網絡攻擊檢測數學模型。

所構建模型的創新點：

1)噪聲去除；

2)網絡信息歸一化處理；

經上述實驗驗證，所構建數學模型在網絡攻擊檢測率、網絡攻擊誤報率、網絡攻擊檢測時效性等方面均優于基于行為分析的網絡攻擊檢測數學模型、基于流量和IP熵特性的DDoS攻擊檢測數學模型和基于蟻群算法的網絡攻擊檢測數學模型，采用本文所構建的數學模型可以在高網絡攻擊檢測率、低網絡攻擊誤報率、高網絡攻擊檢測時效性的情況下更好的完成對網絡攻擊的檢測。