基于改進動態規劃的無人機搜尋航跡規劃研究

錢 宇，祝禎祎

(中國民用航空飛行學院，四川 廣漢 618307)

1 引言

近幾年來，世界范圍內出現越來越多的自然災害，例如洪水、地震、臺風等，這些災害覆蓋面積廣、房屋摧毀數量多。無人機作為一種新興無人駕駛技術的載體，具有重量輕、航時長、機動性能好等優勢，在救援的過程當中發揮越來越重要的作用[1]。為了滿足無人機快速高效地進行定點搜尋工作[2]，需要根據已知的障礙物環境和其物理性能約束規劃一條耗時最少、航程最短的航跡。

針對無人機航跡規劃技術，國內外學者提出了很多高效的航跡規劃算法，主要分為傳統經典算法和現代智能算法[3]。傳統經典算法包括人工勢場法[4](Artificial Potential Field，APF)、模擬退火算法[5](Simulated Annealing Algorithm，SAA)等。這類方法容易陷入局部最優解，在規劃空間較大時搜索效率低，相比之下，現代智能算法收斂程度更好，時間復雜度更小，應用范圍更廣。其中包括A*算法[6]、遺傳算法[7](Genetic Algorithm，GA)、蟻群算法[8](ACO)等。經過幾十年的發展，這些算法在某些具體場景下仍然有一定的局限性，因此提出了許多改進算法。程澤新等[9]將遺傳算法用于無人機航跡規劃中，對進化變異的策略進行改進并結合啟發式搜索方程，可以加快收斂的速度并更有效地獲取可行路徑，但是由于是基于概率的選擇機制，仍然存在陷入局部最優的可能性。劉永琦等[10]提出在三維環境中修剪擴展節點，降低傳統A*算法的網格節點計算量，提高了路徑搜索速度，然而并未詳細闡釋改進A*算法的搜索流程。

動態規劃算法(Dynamic Programming，DP)是由美國數學家R.E.Bellma求解多決策問題時提出的一種優化算法，特點在于搜索效率高，結果穩定可靠，從而受到廣泛的關注。它將一個問題分解成若干個互相聯系的階段，對每個階段作出決策，逐個求解，但是在實際應用中性能會受到影響。譚峻強等[11]詳細地闡述了動態規劃算法的基本思想，并將其用于求解最短運輸距離，耗費時間短，結果清晰明了；但是當問題的規劃空間變大時，時間復雜度也會相應地增大。孫健等[12]在突發威脅的環境下，結合動態規劃算法和切線法可以實時地獲得一條合理規避障礙物的航跡，但是飛行過程中需要多次切換方向并且存在多余的航跡點，整個飛行航跡距離相應地變長。

為了解決航跡規劃耗時長以及冗余節點的問題，研究首先利用雙向動態規劃算法把搜索空間重新規劃為兩個對稱區域，減少參與多階段決策的狀態點總數；之后基于優化后的搜索區域，在區間內驗證度量函數滿足四邊形不等式并找到使節點之間歐氏距離最小的決策范圍，進一步減少冗余節點的數量，以期得到一種在航跡最優性和規劃速度上效果更好的規劃算法。

2 無人機航跡規劃建模

無人機從起始點到終止點的搜尋過程中，為了減少耗費的時間，需要在空間中規劃一條最優的飛行路徑。選擇在三維空間中對無人機的靜態航跡進行仿真建模。假設條件如下：

1)無人機的飛行方向不會指向初始點。

2)只能在規定的空間內進行路徑規劃。

3)忽略無人機的大小，將其簡化為質點。

4)搜尋過程中只考慮障礙物的威脅。

2.1 三維空間柵格化

為了能夠計算出滿足約束條件的航跡規劃

表達式，需要對無人機搜索的整個空間進行離散化

{(x，y，z)|a≤x，y，z≤bx，y，z∈Z}

(1)

在三維坐標系中，令無人機經過的航跡點qi(i=1，2…n)的坐標為(xi，yi，zi)；障礙物區域表示為(xj，yj，zj，r)，整個規劃空間如圖1所示。其中空心正方體表示為空間離散后的節點，紅色實心正方體A和B分別表示無人機搜尋過程的起始點和終止點，球體代表空間中的障礙物區域。

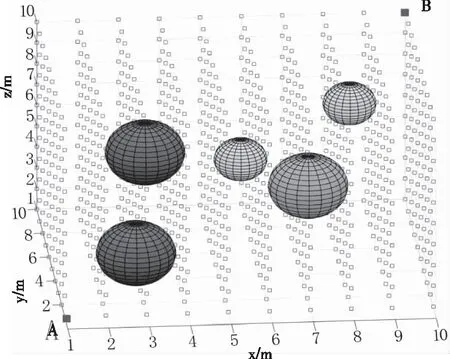
圖1 無人機航跡規劃空間柵格化

2.2 約束條件

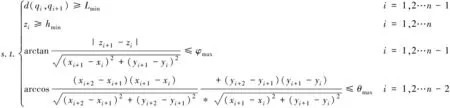
研究考慮最小航跡長度、最大轉彎角、最大爬升角/下降角、最低飛行高度等約束。約束條件如下

式中，Lmin為無人機最小航跡長度，θmax為無人機最大轉彎角，φmax為無人機最大爬升角/下降角，hmin為最低飛行高度。qi為空間航跡點，(xi，yi，zi)為航跡點的坐標，d(qi，qi+1)為相鄰航跡點(qi，qi+1)的歐氏距離。

2.3 代價函數

航跡規劃的代價函數[13]是評價航跡優劣的一個重要的標準。影響三維航跡規劃的主要因素包括航跡長度代價L、飛行高度代價H和威脅區的威脅代價T，分別表示為

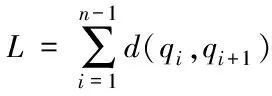
(6)

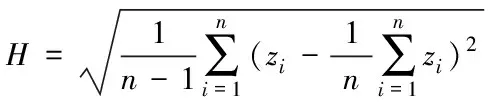
(7)

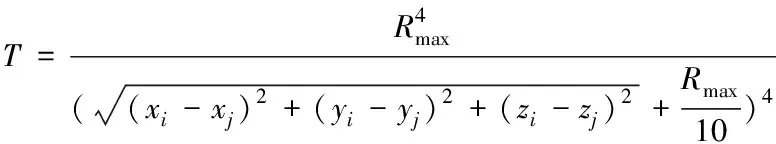
(8)

這里Rmax表示威脅區的最大作用距離，k表示威脅區的個數， (xj，yj，zj)表示威脅區中心坐標。

航跡總代價J與相應的權系數w1、w2和w3表示為

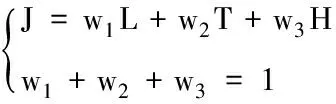
(9)

可以得到無人機航跡規劃模型

min(w1L+w2T+w3H)

(10)

3 航跡規劃算法

動態規劃算法通常將問題劃分為若干個相互關聯的階段，通過找到使每個階段都達得最優效果的決策序列，來獲得整個問題的最優解。利用動態規劃算法進行無人機搜尋任務航跡規劃，在優先考慮整體的思路下，確定每個狀態的最優值，最終可以得到整條搜尋航跡的最優策略。

無人機航跡規劃中，在初始狀態確定，而結束狀態不確定的情況下，自底向上的逆序法效率更高；相反在結束狀態確定，而初始狀態不確定的情況下，自頂向下的順序法效率更高[14]。因此在航跡規劃中確定了初始狀態和結束狀態的基礎上，順序法和逆序法都可以使用。研究采用逆序法進行建模分析。

無人機從初始點A搜尋到終止點B的總航跡，可以劃分為n個階段，每個階段表示為k(k的取值為1，2…n)，第k階段的狀態為fk；第k階段狀態為fk的決策變量表示成vk(fk)。若確定了第k階段的狀態fk和選擇的決策vk(fk)，則k+1階段的狀態fk+1也可以確定，常用式子fk+1=M(fk，vk(fk))表示。規劃過程表示為：

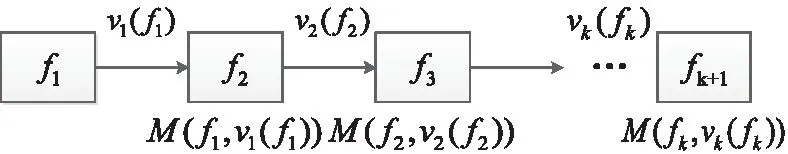
圖2 搜尋規劃流程圖

航跡點和距離信息存儲在動態規劃表中，從終點開始利用逆序法向前進行規劃，依次找到花費最小的前向節點。將指標函數中第k階段的狀態fk到第k+1階段的狀態fk+1之間的花費定義為兩點之間的歐氏距離d(fk+1，fk)，第一階段到第k階段花費度量值之和w表示為

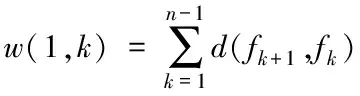
(11)

已知階段1的狀態A和階段n的狀態B，單向動態規劃的逆序法模型

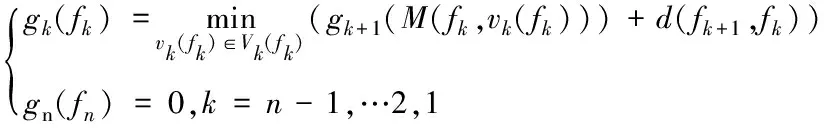
(12)

gk(fk)表示第k階段末狀態fk到結束點B的最優指標函數值；gn(fn)代表結束點狀態B。同理，順序法的動態規劃模型可以表示為

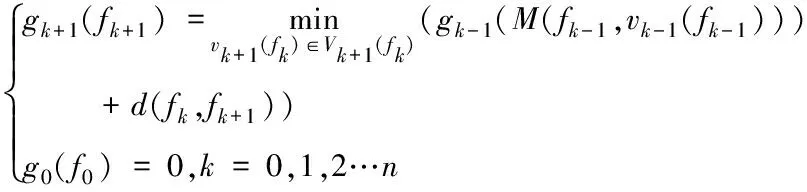
(13)

其中，gk+1(fk+1)表示為初始狀態A到第k+1階段末狀態fk+1的最優指標函數值，g0(f0)代表初始點狀態A。當搜尋出從A到B的最優航跡時，其中每一段子航跡也是最優的，滿足動態規劃的最優子結構性質；函數通過作用于后部子過程，得到一個在以往計算中的最優狀態，不會對下一步的決策起到影響，滿足了無后效性原則；通過將航跡規劃得到的狀態存儲在內存表中，略增加了空間復雜度，但解決了子問題的重疊性。

4 算法改進策略

4.1 狀態總數優化

動態規劃算法在搜尋過程中，需要遍歷整個搜索空間中的狀態點尋找最短航跡，當問題規模較小時， 可以取得很好的效果， 但是當規劃空間增大，問題中狀態總數增多時， 規劃耗時變長。針對此問題，雙向動態規劃算法在保證全局最優的同時，也提高了算法的規劃速度。

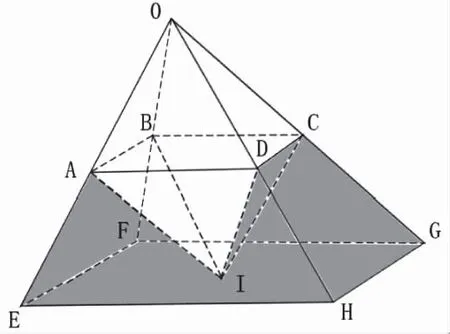
圖3 雙向動態規劃算法分析

如圖3所示，單向動態規劃的計算空間區域為五面體OEFGH，但是雙向動態規劃的計算空間區域為五面體OABCD與五面體IABCD之和；圖中灰色區域是雙向動態規劃相對于單向動態規劃少計算的狀態區域；令順序法和逆序法的最優交匯處在第k階段，選取狀態點的過程需要滿足

qk∈N∩qk∈B=1

(14)

其中qk表示為第k階段選擇的狀態點，順序狀態點存儲在內存表N中，逆序狀態點存儲在內存表B中。

4.2 狀態轉移過程優化

動態規劃算法通過計算每個階段中所有符合約束的狀態點來尋找最短路徑；狀態轉移過程就是，把原問題分解為兩個子問題，利用求解過的前一狀態和此狀態上的決策得到當前的狀態。狀態轉移所涉及的狀態數目影響了動態規劃算法的時間效率。因此在優化決策量的基礎上減少所涉及的狀態數目，提高運算量。

將狀態轉移中度量值定義為w(i，j)，航跡規劃過程中的狀態轉移方程表示為

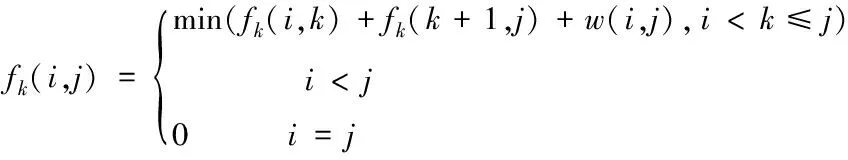
(15)

度費用，fk(i，j)表示區間(i，j)上的最短路徑。在區域OABCD中，根據式(11)度量函數w(i，j)屬于單調遞增，區間(i，j)包含于(i′，j′)，可以驗證其滿足包含關系單調性

w(i，j)≤w(i′，j′)，(i，j)?(i′，j′)

(16)

在式(16)的基礎上對距離函數w進行分類討論，得到度量函數w(i，j)滿足四邊形不等式：

w(a，c)+w(b，d)≤w(b，c)+w(a，d)a≤b≤c≤d

(17)

根據式(16)和(17)，通過歸納法可以得到，最短路徑函數也滿足四邊形不等式

fk(a，c)+fk(b，d)≤fk(b，c)+fk(a，d)

(18)

Pk∈{(x，y，z)|a≤x，y，z≤bx，y，z∈Z}為第k階段決策集合，令p(a，b)為fk在(a，b)區間內取最小值時的決策，通過反證法可以得到

p(a，b-1)≤p(a，b)≤p(a+1，b)

(19)

根據式(19)，在保證航跡距離最短的情況下，雙向規劃的決策范圍大大縮小，進一步排除了冗余的節點，存儲計算過程更加高效。優化后的狀態轉移函數可以表示為

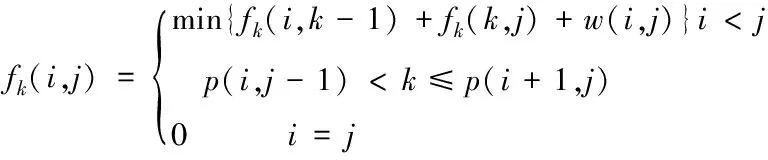
(20)

其中狀態轉移方程的區間長度L=j-i，v(i+1，j)和v(i，j-1)的長度為L-1，區間的長度為n個，對于確定的長度L，其包含的狀態有n個，因此時間復雜度為O(n2)。改進之前，根據式(15)可知算法的時間復雜度為O(n3)。在改進過程中，分析狀態之間的關系，得出最優決策具有單調性質，因此在計算過程中減少了狀態轉移考慮的狀態數，提高了算法的時間效率。

4.3 改進動態規劃算法流程

改進動態規劃算法計算流程如下：

1)初始化數據，包括搜索空間、障礙物坐標和無人機約束函數。

2)三維空間柵格化，若搜尋點不在障礙物區域內，通過式(14)確定順序法和逆序法交匯階段k。

3)在順序法的基礎上，結合改進狀態轉移函數式(20)搜尋前k階段的路徑點，利用d(fk+1，fk)計算距離并把信息全部存儲在內存表N中。逆序法同理，將數據都存儲在內存表B中。

4)若內存表N和B中存在相同的狀態集P，則把兩個表中存儲的狀態點和P連接起來，計算相應的距離。若不存在，則返回步驟2)。

5)找出最小的距離，并輸出。

算法流程圖如圖4。

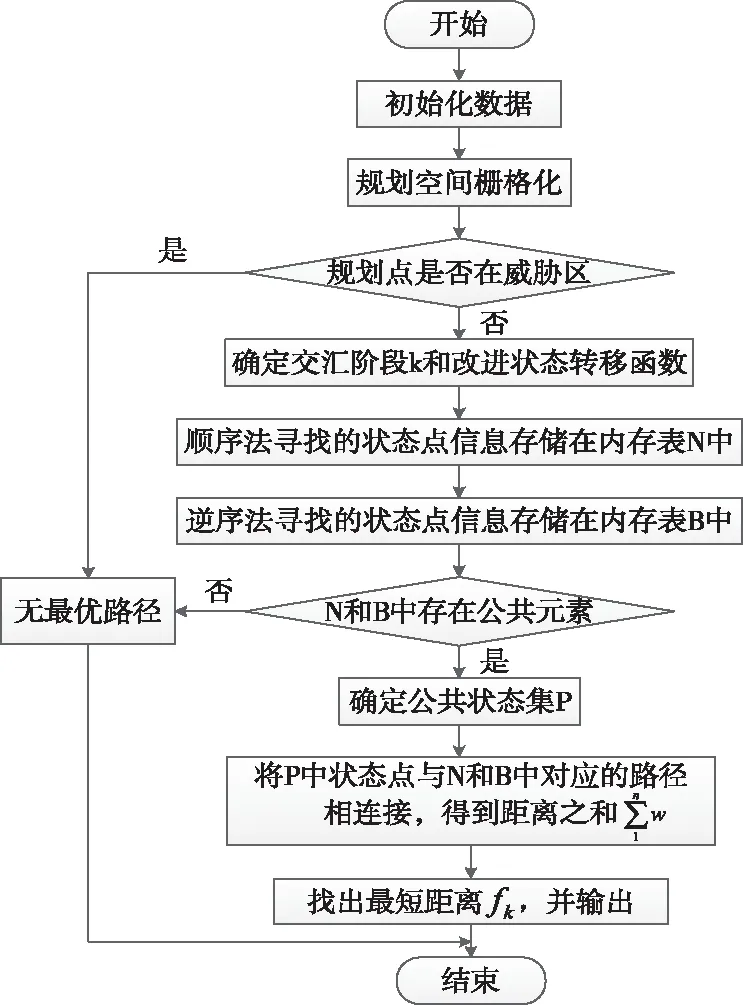
圖4 改進動態規劃算法流程圖

5 仿真與結果分析

為了驗證算法的性能，研究利用遺傳算法、動態規劃算法和改進動態規劃算法進行了仿真計算。

仿真條件為：無人機的起始點為(1m，1m，1m)，終止點為(10m，10m，10m)；當無人機在搜尋過程中，可以利用立體攝像機獲取障礙物的位置坐標，最小航跡長度為1m，最大轉彎角50°，最大爬升角60°。障礙物的位置信息如表1。

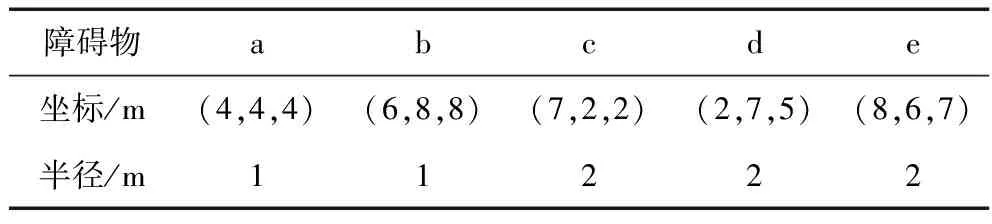
表1 障礙物信息表

仿真結果航跡對比如圖5、圖6，不同算法的航跡總長度及計算時間如表2所示。

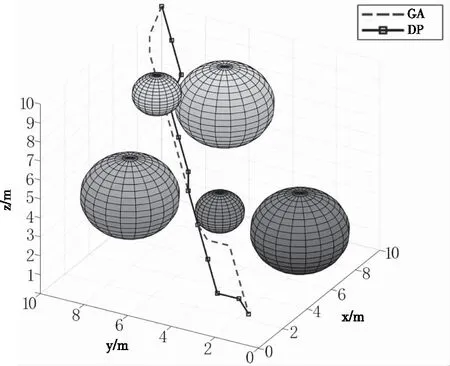
圖5 DP與GA算法航跡規劃對比圖

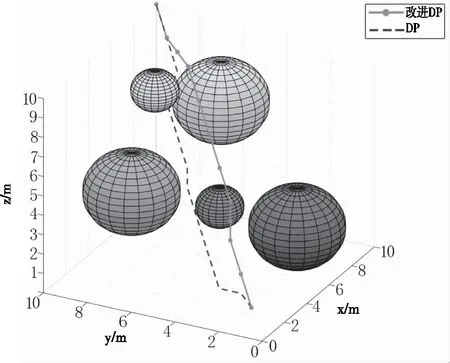
圖6 改進DP與DP算法航跡規劃對比圖

圖5顯示出遺傳算法規劃了一條可行的搜尋航跡，但是相對于動態規劃算法，不是一條最優航跡，主要是遺傳算法在航跡規劃后期收斂速度變慢，容易陷入局部最優，使得計算效率變低；無論是在規劃速度還是航跡最優性都是動態規劃算法更好，利用空間換取時間，存儲了每個狀態點之間的距離，但是還會產生冗余。圖6中，改進動態規劃算法計算的狀態點的數量相比于動態規劃算法更少，解決了空間占據過多的問題，因此規劃速度更快，消耗時間更短；并且通過狀態轉移優化策略減少了冗余節點，航跡長度更優。三種算法的仿真結果如表2。

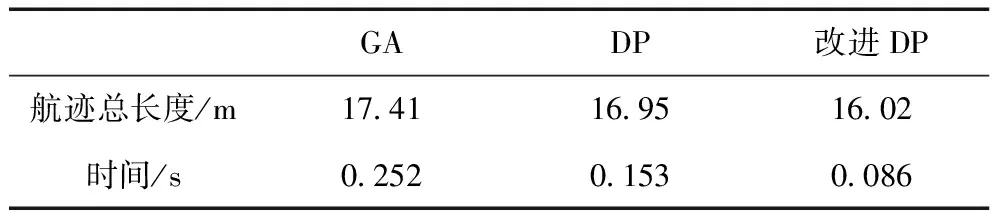
表2 不同算法仿真結果對比

結果表示，在航跡點數量方面，改進DP算法相對于GA算法減少7.9%，相對于DP算法減少5.4%；在時間效率方面，改進DP算法相對于GA算法提高65%，相對于DP算法提高43%。仿真結果驗證了改進動態規劃算法耗時短，搜尋距離小。

6 結論

1)改進動態規范算法減少了狀態轉移過程的計算量和存儲量，加快了規劃速度；優化了航跡節點數量，縮短了整個搜尋的時間。改進動態規劃算法能夠很好的規劃一條代價最小、航路最優的航跡。

2)針對動態規劃算法存在維數爆炸，耗時長的問題，結合雙向動態規劃算法的并行搜索特點和決策變量的優化策略得到一種改進動態規劃算法，并將其運用在無人機災后定點搜尋任務規劃中。