“穿越沙漠”中的最大資金剩余量問題探究

余 馨，陳 云，俞旭燕

（徐州工程學院 a. 金融學院； b. 信息工程學院， 江蘇 徐州 221018）

現有一種“穿越沙漠”游戲：玩家可根據一張地圖，在沙漠中從起點出發行走至終點，沙漠中有晴朗、高溫、沙暴三種天氣情況，玩家可利用初始資金購買一定數量的水和食物，也可在礦山、村莊補充資金或資源，最后在規定的時間內到達沙漠終點，并盡可能保留更多的資金。整個游戲共六個關卡，每個關卡的參數設定、天氣狀況、路線地圖都不相同[1]。本文擬對2020 年全國大學生數學建模大賽B 題“穿越沙漠”中的最大資金剩余量問題進行研究。

1 解決問題一的動態規劃算法

賽題一包括第一關和第二關，在規定的時段內每天天氣狀況事先全部已知。

1.1 動態規劃與狀態轉移

動態規劃的前提是狀態轉移。在沙漠行走，離不開水和食物資源。玩家在每天的資源保有量基礎上做決策，將決定下一天的資源剩余量，形成狀態轉移。

玩家選擇停留、行走或挖礦，對資源的消耗量分別是基礎量的 1、2、3 倍，故設 i=1，2，3，xki∈（1，0）表示第 k 天對 i 的選擇與否。

記αj、βj（j=1，2，3）為晴朗、高溫、沙暴天氣對水和食物的基礎消耗量，ykj∈（1，0）表示第 k 天是否為第j 種天氣，這均為已知參數[1]。

又設A、B 為在起點購買水和食物的數量，ak、bk為第k 天在村莊購買水和食物的數量。

計算第n 天水和食物的剩余量Sn和Wn：

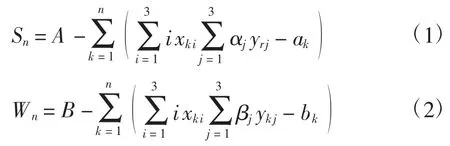
在時間遞增的情況下，可運用式（1）、（2）不斷更新玩家所處位置并計算下一天水和食物的保有量。

1.2 已知天氣狀態的最大資金剩余量模型

變量設置：f 表示剩余資金量；T 表示從起點到終點的歷時天數，t 表示挖礦天數；其他設置同1.1 節。

目標函數為資金剩余量：

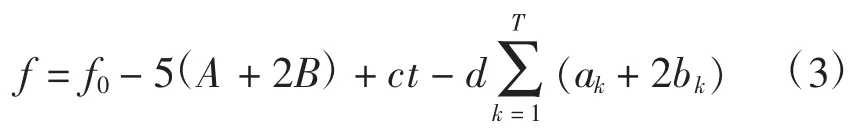
優化方向為max f。其中：f0=10 000 元為初始資金，c 為給定的挖礦基礎收益，d=10 表示在村莊補充資源需支付基準價格2 倍的資金。

在問題一中，c=1 000 元/天。

根據游戲規則[1]設置約束條件：

體現資源不能耗盡。要求恰在終點處耗盡，即ST=WT=0，有利于最大化f max。

體現負重上限約束。初始時刻也受此約束，而達到3A+2B=1 200 可對f max 提供保障。

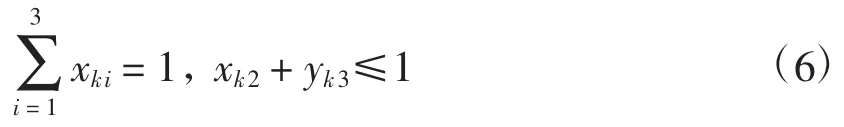
體現0-1 變量的單一選擇性，以及沙暴天氣不能行走。

體現所耗時間的限制。問題一中T0=30 天。

1.3 第一關的求解

30 天內天氣狀態已知[1]，玩家選擇的行走狀態分成3 種：停留、行走和挖礦。用動態規劃求解第一關，需建立狀態轉移方程[2]。

方程中的變量解釋：time 為時間，time-1 為前一時刻的時間狀態，v 表示水與食物的質量，i 為水的消耗量，j 為食物的消耗量。Need 為消耗，_s表示水的屬性，_w 表示食物屬性，s′為增加的水質量，w′為增加的食物質量。下面分不同情況建立四維DP 狀態轉移方程。

第一種情況，天氣不是沙暴時選擇行走：

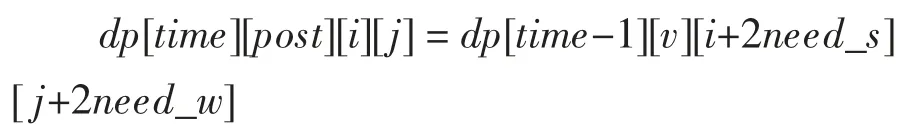
表示下一時刻的水與食物的消耗量在前一時刻水消耗量的基礎上增加兩倍基礎消耗。

第二種情況，路過村莊時玩家選擇補給水與食物：

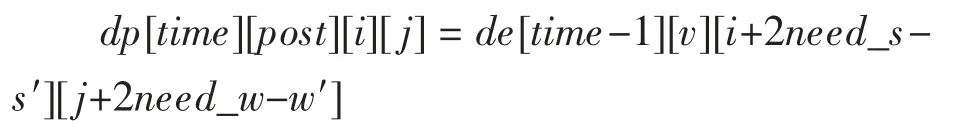
表示所耗資金為原先兩倍，時間不增加。其中增加的補給量為負數，消耗量為正數。

第三種情況，路過礦山時，選擇挖礦：

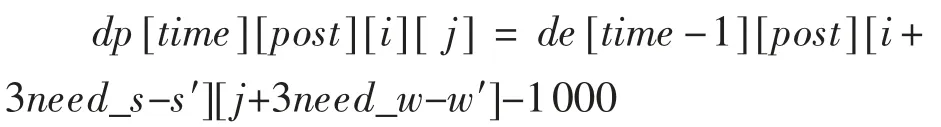
表示當天不能挖礦，下一狀態停留在原地，并獲基礎收益。

第四種情況，停在原地：

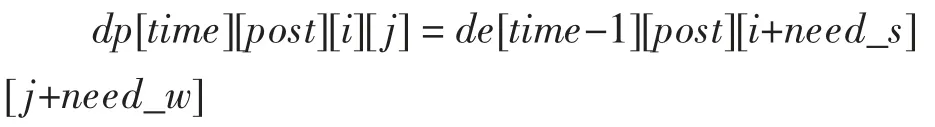
此時，只有一倍基礎消耗，時間增加，位置不轉移。

運用Java 進行編譯，運算結果如表1 所示。最大資金剩余量為10 470 元。具體行走路徑如圖1 所示。

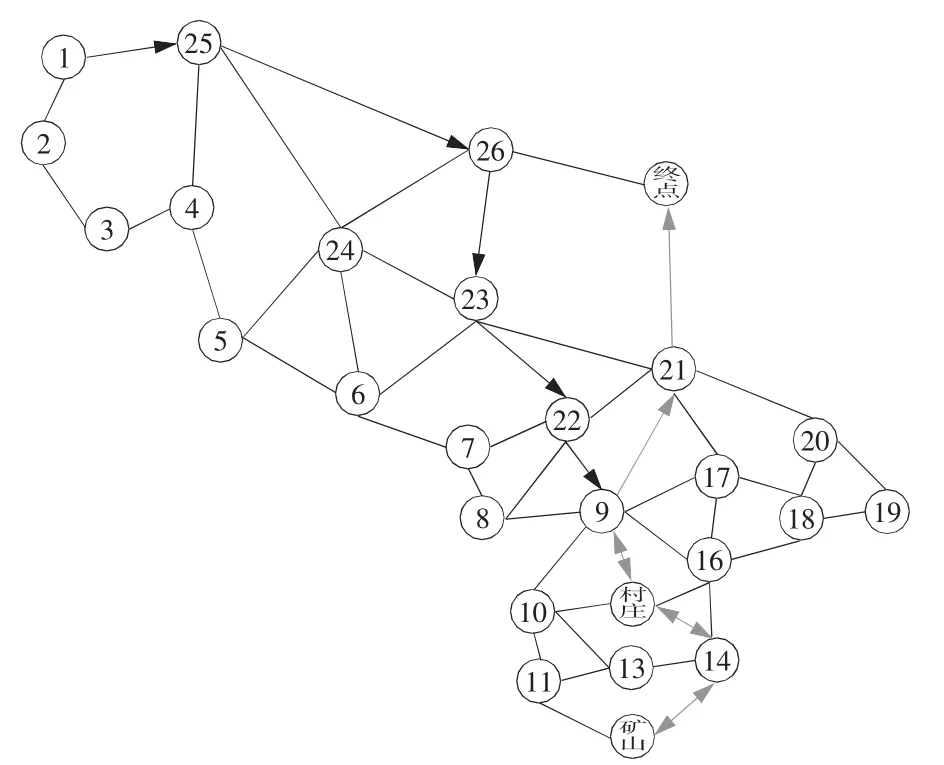
圖1 第一關的具體路徑

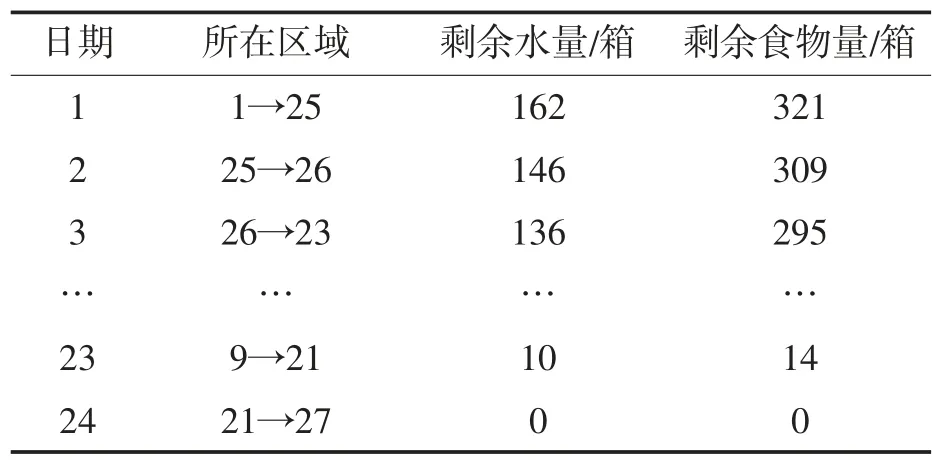
表1 第一關的部分運算結果

運算結果顯示，玩家從出發到終點耗時24天。其中晴天出現7 次，6 次選擇行走；高溫天氣出現12 次，5 次選擇挖礦；沙暴天氣出現5 次，其中1 次選擇挖礦（沙暴天氣必停，但可挖礦），4 次選擇停留。

1.4 第二關的求解

第二關地圖[1]的區域排列類似于矩形分布，從起點1 到礦山30 的最短路徑需要走7 步。由相鄰區域的交換律可知，固定步數時，7 塊相鄰區域等效，故可剔除以下屬于冗雜多余的區域：

3，4，5，6，7，8，11，12，13，14，15，16，20，21，22，23，24，31，32。

起點到村莊需要8 步，故刪除以下區域：

17，25，33，34，41，42，49，50，51，57，58，59。

村莊到終點刪去繞行區域：40，48。

運用1.3 節的狀態轉移方程，代入目標函數，運用Java 進行編譯，運算結果如表2 所示，最大資金剩余量為12 730 元。具體行走路徑如圖2所示。

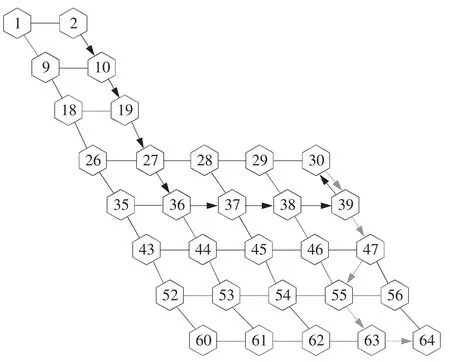
圖2 第二關的具體路徑

表2 第二關的部分運算結果

玩家的策略為：礦山較遠，挖礦前要補資源，所以先到村莊，后到礦山。挖礦6 天折返回村莊又補資源，再經2 步到第二座礦山挖礦7 天，然后2步到達終點。

2 解決問題二的遺傳算法

問題二包括第三關和第四關，玩家僅知道當天的天氣狀況，可據此決定當天的行動方案。

2.1 馬爾科夫鏈天氣預測模型

根據當天的天氣狀況，可利用馬爾科夫鏈模型預測未來的天氣狀況。

以不出現沙暴的第三關[1]為例。設當天為晴天時，下一天是晴天和高溫的概率分別為p 和1-p；當天為高溫時，下一天是高溫和晴天的概率分別為 p′和 1-p′，則稱

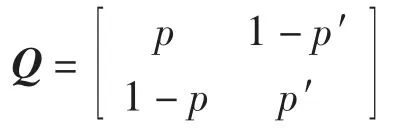
為一階狀態轉移概率矩陣。其中的概率值滿足0.1的梯度下降規則，即

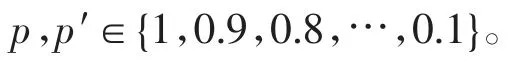
若初始的狀態概率分布為P0，則n 天后的狀態概率分布為Pn=QnP0。當n 趨向于無窮時，Pn趨于恒定。這表明，用馬爾科夫鏈對天氣狀態進行預測，與初始狀態無關。

2.2 問題二的最大資金剩余量模型

問題二的優化模型與問題一相同，仍為式（1）～（7），只是部分已知參數有所不同[1]：第三關的挖礦基礎收益為c=200 元/天，行走限時為T0=10天；第四關則仍為 c=1 000 元/天，T0=30 天。

此外，第三關的地圖中有礦山但沒有村莊，故只針對資金進行補充，不考慮資源補給，即所有的ak=bk=0；第三關不出現沙暴天氣，所有yk3=0，涉及的下標僅取j=1，2 即可。

2.3 第三關的求解

先用Java 模擬出不同概率下設定的1 000 組數值解，多次嘗試之后得出各種結果，再用遺傳算法[3-4]，搜索出不同組中10 日天氣情況不同的最優資金剩余量[5]。遺傳算法的具體過程如下。

Step1：編碼方案

行為狀態的染色體個體為三進制串，以0、1、2分別表示停留、行走和挖礦。天氣狀態的染色體個體為二進制串，以0、1 分別表示晴天和高溫。

Step2：種群初始化

隨機生成1 000 組染色體，根據梯度下降原理，設定晴朗天氣出現的概率為不同的p，高溫天氣則為對應的1-p。

具體以p=0.7 為例，利用馬爾科夫預測模型[6-7]求解10 日內不同天氣的數學期望。

Step3：初始群體的確定

種群規模N=1 000，交叉概率Pc=0.9，變異概率Pm=0.1，迭代次數m=1 000；

本文所選取的初始化群體為Java 在限定區間內隨機模擬生成。按照這種解法，可以選出1 000 組個體組成解。

Step4：適應度函數

適應度函數即目標函數（3）。計算隨機模擬的1 000 組天氣狀況下的最大資金保留量，計算每個個體的適應值Fitness 相當于通過自變量求得適應度函數的值，然后判斷是否應刪除質量差的個體。

Step5：約束檢驗

檢驗約束條件（4）～（7），剔除不合格的行為狀態。

Step6：評價個體適應度

對不同組天氣狀態所生成的二進制串和人的行為方式進行解碼處理，可得到不同天氣狀態下的表現型，由個體表現型計算對應個體的目標函數值。根據適應度函數最大的條件，求出個體適應度。

Step7：選擇函數

運用最佳保留選擇，隨機概率設定為0.95。將當前種群中適應度最高的個體放到下一種群中。

Step8：個體的交叉與變異

從染色體串中選擇NPc 個個體進行交叉選項，本文交叉方法為部分染色體段進行交叉，并檢查交叉結果是否滿足合法性，即在不同天氣狀態下玩家所對應的方式能否正確表示，若不符合則再次交叉或取消該操作。

Step9：循環

變異是根據變異概率更改染色體串中某個值使之變為不同天氣狀態和人的行為狀態。

完成交叉變異后，代入適應度函數，選擇再生個體，適應度高的個體即剩余資金留用數量高的被留下，一直進行循環。

Step10：終止計算

滿足停止準則時終止計算，輸出最優結果。

運用遺傳算法進行具體運算[8]，設置初始晴天出現的概率為0.7。迭代1 000 次后最大資金剩余量為9 189，4 天的天氣情況為“高溫，高溫，高溫，晴朗”。

考慮是否要挖礦：挖礦需繞道兩天，至少多付出 55×2×2 ＝220 元（晴天），而挖礦一天收益最多為200－55×3 ＝35 元（晴天），10 天中至多有5 天可以挖礦，獲得收益的上限為35 × 5 ＝175元。由于收益小于付出，所以放棄挖礦。第三關的具體行走路徑如圖3 所示。

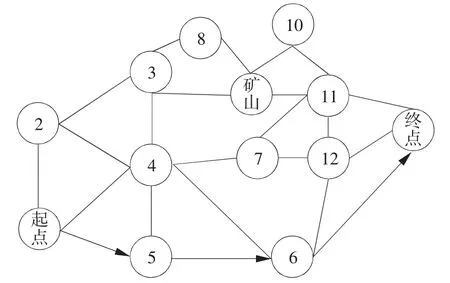
圖3 第三關的具體路徑

綜上，一般情況下第三關玩家的最佳策略為：晴天必行走，出現高溫則停留，若連續兩天都是高溫，則用馬爾科夫鏈分析第三天的天氣情況，經狀態轉移概率計算[9-10]，當第三天晴朗概率超過高溫50 %時選擇行走，否則繼續停留。

2.4 第四關的求解

第四關既有礦山，也有村莊，且出現沙暴天氣的概率較小[1]。求解方法與第三關相仿。

設置初始沙暴出現概率為0.1（較低值），運用Java 仿真模擬，沙暴出現的概率為0.1～0.4，依據收益的數學期望，經遺傳算法求解，得到最大資金剩余量為1 1265 元，8 天的天氣情況為“沙暴3天，晴朗 4 天，高溫 1 天”。

分析求解結果，可得最佳策略：晴朗必走，出現高溫適合停留，若連續出現高溫天氣，第一天選擇停留，根據貝葉斯概率分布可得未來一天各種天氣出現的概率，若出現高溫天氣的概率超過0.64 則停留，若低于0.64 則行走，遇沙暴時停留，有礦山則挖礦。