不同數量鉆孔瓦斯抽采有效區域數值模擬分析

陳月霞，褚廷湘，陳 鵬

(華北科技學院 a.應急技術與管理學院； b.安全監管學院，河北 廊坊 065201)

通過鉆孔進行瓦斯抽采是防治瓦斯災害的主要措施之一。然而我國煤層滲透率普遍較低，且因煤層的多孔介質屬性、賦存狀態、水分含量等因素導致煤層處于氣固液耦合狀態，加劇了瓦斯流動的復雜性。由于鉆孔布置參數的選取多依靠經驗獲得，并非最優參數，導致鉆孔抽采瓦斯的效率不高[1-5]。

有效抽采半徑是煤礦鉆孔合理布置的重要依據[6-8]。王兆豐等[9]采用數值模擬方法分析了有效抽采半徑和抽采時間的關系；袁亮等[10]采用數值模擬方法綜合分析了地面垂直鉆孔的經濟投入與瓦斯抽采效果之間的關系，確定了地面垂直鉆孔終孔合理間距；唐明云等[11]依據同一抽采時間留下空白帶的面積及消除空白帶所用的時間，研究了鉆孔的布置方式；林柏泉等[12]探討了不同垂直地應力、初始瓦斯壓力，以及初始滲透率等參數對鉆孔有效抽采區域的影響；范超軍等[13-14]分析了滲透率對瓦斯抽采的影響，建立了流固耦合模型；郝富昌等[15]采用數值模擬方法確定了不同軟硬度煤層的有效抽采半徑及影響因素；許江等[16]采用物理模擬方法分析了順層鉆孔布置間距對瓦斯抽采效率的影響；劉三鈞等[17]推導了瓦斯壓力和瓦斯抽采率之間的關系，提出了利用相對壓力測算有效抽采半徑的方法；李波等[18]利用壓降法通過試驗研究了鉆孔的有效抽采半徑，并分析了有效抽采半徑和影響半徑的演化規律；ZHANG Chaolin等[19]通過自主研發的瓦斯抽采試驗裝置，物理模擬了單個和多個鉆孔抽采時瓦斯的流動規律,并研究了不同鉆孔數量對有效抽采半徑的影響。

上述科研人員在抽采鉆孔的間距、數量及形狀等方面開展了相關研究，這為確定煤層有效抽采半徑及鉆孔合理布置提供了參考。但是基于真三軸應力狀態，考慮不同鉆孔數量、鉆孔的疊加效應，采用三維數值模擬方法，以有效抽采區域體積為指標，對比分析不同鉆孔數量對抽采效果影響的文獻較少。因此，筆者基于所建立的流固耦合模型，考慮煤層所受的真實應力狀態，采用三維數值模擬方法分析不同數量鉆孔抽采時有效抽采區域的時空演化特征，分析鉆孔布置數量對煤層瓦斯壓力及有效抽采體積的影響規律，以期對現場煤礦瓦斯抽采鉆孔合理布置參數的設置提供指導。

1 流固耦合模型

在數值模擬中采用筆者已建立的流固耦合模型，具體推導過程見文獻[20]。

應力場方程見式(1)：

(1)

式中：G為剪切剛度，G=D/2(1+ν)；D為等效煤體彈性模量；u為位移，ui,kk為位移張量形式，且第1個下標i表示u的i方向分量，第2個下標k表示對ui求i方向偏導數，第3個下標k表示對ui,k求k方向偏導數；ν為泊松比；α為孔隙對應的Biot有效應力系數；β為裂隙對應的Biot有效應力系數；pm,i、pfg,i分別為基質瓦斯壓力、裂隙瓦斯壓力，下標i表示i方向的分量；K為體積模量；εs為吸附導致的應變，εs=VLpm/(pL+pm)；f為體應力。

滲流場方程見式(2)～(4)。其中，基質中煤層氣運移方程為：

(2)

裂隙中氣體和水的流動方程分別為：

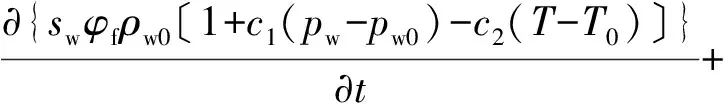
(3)

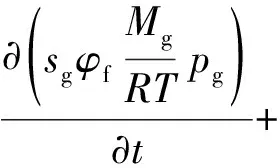
(4)

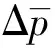
式(3)中：sw為水的飽和度；φf為裂隙率；ρw為水密度；pw為水壓力；k為滲透率；krw為水的相對滲透率；μw為水的動力黏度系數；pfw為裂隙水壓力；g為重力加速度；?z=(0,0,1)。

式(4)中：sg為氣體飽和度；pg為氣體壓力；krg為氣體的相對滲透率；μg為瓦斯動力黏度系數。

式(2)～(4)中，各量符號下標0表示初始值。

2 數值模擬幾何模型和邊界條件

依據文獻[20]中煤礦參數，設置煤層幾何模型的長寬高分別為40、30、6 m；煤層所受的最大、平均和最小主應力分別為19、13、10 MPa；初始瓦斯壓力為1.2 MPa，抽采負壓為25 kPa；鉆孔邊界采用狄氏邊界條件，煤層邊界滲流為0通量；網格劃分采用自由剖分四面體，鉆孔邊界的最小單元為0.1 m。數值模擬幾何模型如圖1所示(計量單位為m)。

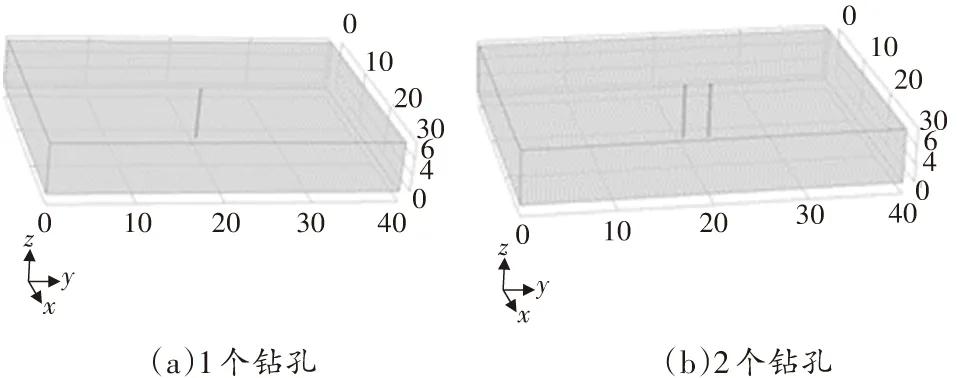
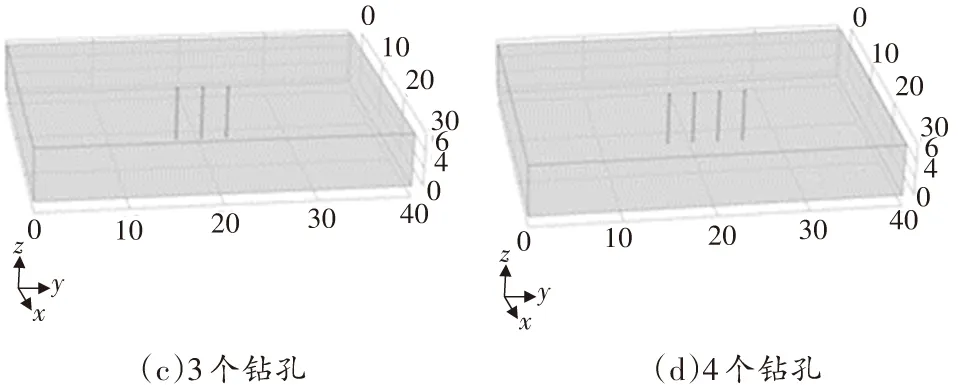
圖1 數值模擬幾何模型

通過模擬計算得到1個鉆孔抽采120 d時的抽采有效半徑為1.4 m。以2.8 m作為鉆孔間距，對單排鉆孔布置形式下的瓦斯抽采情況進行數值模擬。

3 模擬結果分析

3.1 瓦斯壓力演化

在P點(18、20、3 m)位置模擬瓦斯壓力，該點距最近鉆孔的距離為3 m。不同數量鉆孔抽采條件下P點位置瓦斯壓力p隨時間t的變化曲線如圖2所示。

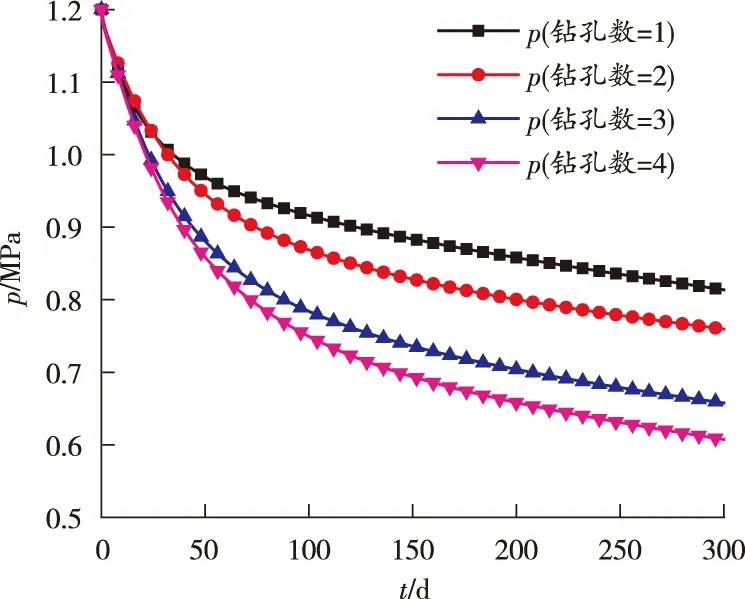
圖2 不同數量鉆孔抽采條件下P點位置瓦斯壓力隨時間的變化曲線

由圖2可知，在瓦斯抽采過程中，鉆孔數量不同時，鉆孔周圍同一位置的瓦斯壓力隨時間的變化不同。抽采初期，P點瓦斯壓力值受鉆孔數量的影響較小。

抽采25 d后，鉆孔數量越多，P點的瓦斯壓力值越小，即下降越快。隨著時間的延長，差距進一步增大。

抽采50 d時，采用1個鉆孔抽采時P點位置的瓦斯壓力下降了19.0%；2個鉆孔抽采時P點位置的瓦斯壓力下降了21.0%；3個鉆孔抽采時P點位置的瓦斯壓力下降了26.6%；4個鉆孔抽采時P點位置的瓦斯壓力下降了28.4%。

抽采120 d時，1個鉆孔抽采下P點的瓦斯壓力下降了24.8%；2個鉆孔抽采下P點的瓦斯壓力下降了29.2%；3個鉆孔抽采下P點的瓦斯壓力下降了36.5%；4個鉆孔抽采下P點的瓦斯壓力下降了39.8%。

由上述P點位置瓦斯壓力與鉆孔數量及抽采時間之間的對應關系，可知P點位置的瓦斯壓力受抽采時間影響較大，即隨抽采時間的增加鉆孔有效抽采半徑和影響半徑均增大，P點位置受多個鉆孔的影響逐漸顯現，瓦斯壓力下降加快，鉆孔數量對瓦斯壓力的影響增大。

在抽采120 d時，x=15 m，z=3.5 m時y方向的坐標與該位置瓦斯壓力p之間的關系曲線如圖3 所示。

(a)1個鉆孔 (b)2個鉆孔

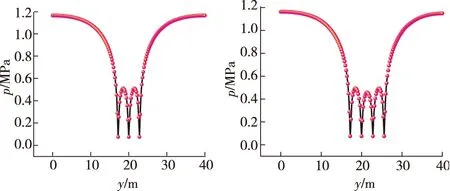
(c)3個鉆孔 (d)4個鉆孔

幾何模型中設置1個鉆孔抽采時，鉆孔所在位置的y方向坐標為y=20.0 m；2個鉆孔抽采時，鉆孔所在位置的y方向坐標為y=20.0、22.8 m；3個鉆孔抽采時，鉆孔所在位置的y方向坐標為y=17.2、20.0、22.8 m；4個鉆孔抽采時，鉆孔所在位置的y方向坐標為y=17.2、20.0、22.8、25.6 m。

由圖3可知，1個鉆孔抽采時，鉆孔附近瓦斯壓力與其y方向坐標關系曲線近似呈現V字形；2個鉆孔抽采時，其關系曲線近似呈現W字形。鉆孔位置處，在抽采負壓的影響下，瓦斯壓力最低，受多個鉆孔疊加效應的影響，鉆孔之間的瓦斯壓力下降較快，隨著與鉆孔距離的增大，瓦斯壓力下降速度減慢。

3.2 有效抽采區域的空間分布及量化分析

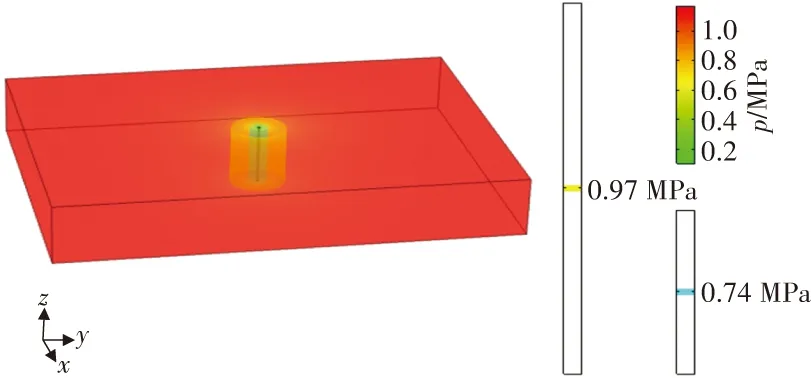
將瓦斯壓力低于0.74 MPa的區域視為有效抽采區域，其半徑稱為有效抽采半徑；依據文獻[18]，將瓦斯壓力降低19%的區域視為抽采影響半徑。通過上述指標，分析有效抽采區域的空間分布。1個鉆孔瓦斯抽采30、60、90及120 d時，瓦斯壓力的空間演化規律如圖4所示。

(a)30 d

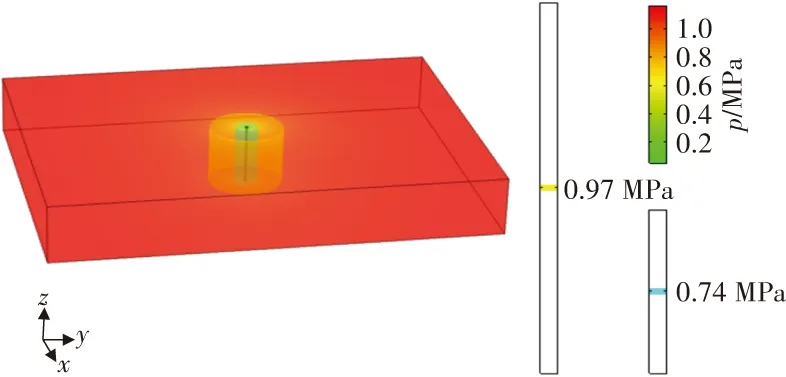
(b)60 d

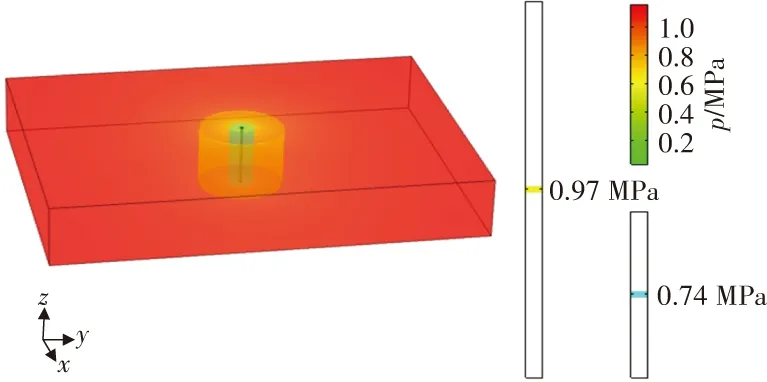
(c)90 d

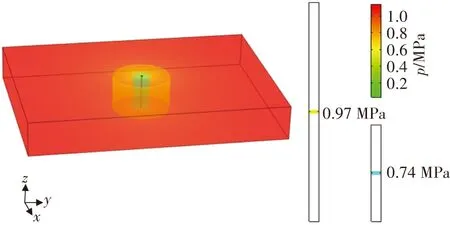
(d)120 d

將臨界值為0.74、0.97 MPa的等壓面云圖用青色和黃色來表示，由圖4可以看出，等壓面均圍繞鉆孔呈圓柱狀分布，圓柱體積隨著時間的增加而增大，影響范圍(瓦斯壓力小于0.97 MPa)遠大于瓦斯有效抽采范圍(瓦斯壓力小于0.74 MPa)。

不同數量鉆孔抽采120 d時瓦斯壓力及有效抽采區域的空間演化規律如圖5所示。

(a)1個鉆孔

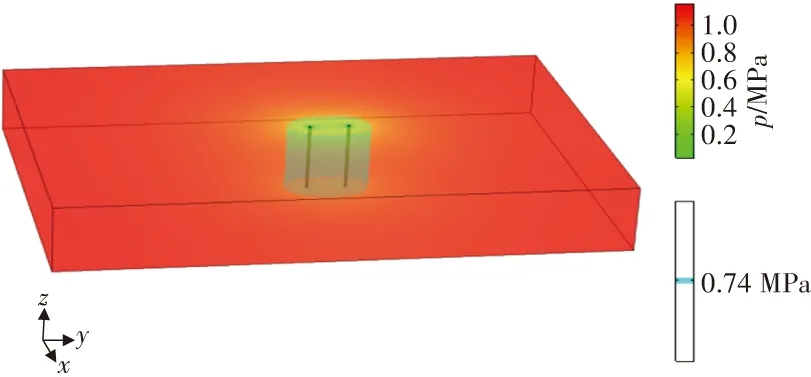
(b)2個鉆孔

(c)3個鉆孔

(d)4個鉆孔

由圖5可知，瓦斯壓力均呈現離鉆孔越近瓦斯壓力越小的趨勢，煤層中設置臨界值為0.74 MPa的等壓面用青色表示。1個鉆孔抽采時，等壓面圍繞鉆孔呈圓柱狀分布，當在同一排布置多個鉆孔時，該等壓面圍繞鉆孔呈橢圓柱狀分布，等壓面以內的瓦斯壓力均已降到0.74 MPa以下。

不同數量鉆孔抽采時有效抽采區域的體積隨抽采時間的演化規律如圖6所示。

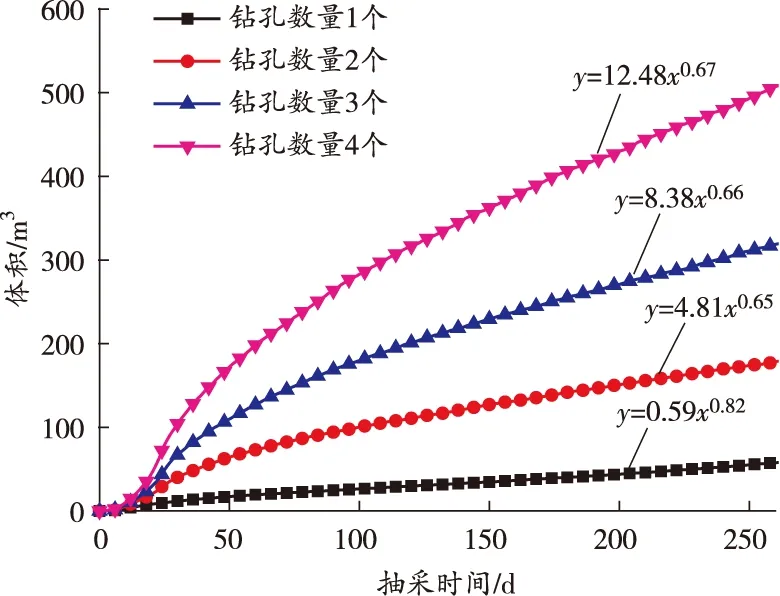
圖6 不同數量鉆孔抽采時有效抽采區域的體積隨抽采時間的演化規律

由圖6可知，瓦斯抽采初期，有效抽采區域體積幾乎均為0，隨著抽采時間的增加，抽采20 d后，有效抽采區域逐漸增大，鉆孔數量越多，有效抽采區域增大越明顯。布置2、3、4個鉆孔抽采200 d時有效抽采區域體積分別是布置1個鉆孔時有效抽采區域體積的3.4倍、6.1倍和9.8倍，發現鉆孔數量與有效抽采區域的體積并非呈線性關系，當鉆孔之間的距離不超出鉆孔影響范圍時，多個鉆孔之間會產生疊加效應，并隨著抽采時間的增加每個鉆孔的影響范圍逐漸增大，疊加效應逐漸增強，使有效抽采區域體積增長較為明顯。

通過對有效抽采區域體積數值擬合，可知有效抽采區域體積和抽采時間呈現y=axb函數關系(其中：y為有效抽采區域的體積，m3；x為抽采時間，d；a和b均為常量參數)。在相同抽采時間下，鉆孔有效抽采區域體積與鉆孔數量并未呈線性關系。

4 結論

1)識別了煤層瓦斯壓力時空響應特征，在抽采初期鉆孔數量對抽采半徑之外煤層瓦斯壓力影響較小，但隨抽采時間的增加，鉆孔數量對其影響逐漸顯現，瓦斯壓力下降趨勢加大。

2)研究了鉆孔數量、抽采時間對有效抽采區域空間分布形態及其范圍的影響。當采用1個鉆孔抽采時，其有效抽采區域圍繞鉆孔呈圓柱狀分布；當采用單排多個鉆孔抽采時，其有效抽采區域呈橢圓柱狀分布。

3)建立了鉆孔數量、抽采時間與有效抽采區域間的函數關系。通過數據擬合發現，鉆孔有效抽采區域體積與抽采時間基本呈y=axb函數關系，在相同抽采時間條件下，鉆孔有效抽采區域體積與鉆孔數量并未呈線性關系。

4)在抽采過程中鉆孔之間會產生疊加效應，隨著抽采時間的增加，疊加效應逐漸顯現，使有效抽采區域體積明顯增大。

5)鉆孔數量、鉆孔間距、排列形狀及鉆孔之間的疊加效應均對瓦斯抽采效果產生影響，但由于篇幅有限，本文僅在考慮鉆孔疊加效應的情況下模擬分析了單排鉆孔數量對瓦斯抽采效果的影響，后續需要完善該研究。