礦業(yè)安全生產事故時間序列的模糊區(qū)間預測

黃 悅，幸福堂，2，石癸鑫，吳孟龍

(1.武漢科技大學 資源與環(huán)境工程學院，湖北 武漢 430081；2.武漢科技大學 冶金礦產資源高效利用與造塊重點實驗室，湖北 武漢 430081)

近年來，隨著采礦業(yè)的發(fā)展，礦業(yè)安全生產事故數量和傷亡人數居高不下，給社會發(fā)展帶來了負面影響。據近年來我國礦山事故統(tǒng)計顯示，2005年至2019年，全國共發(fā)生礦業(yè)安全生產事故3 826起[1]，死亡人數達到14 251人[1]，事故起數和死亡人數超過發(fā)達國家，安全問題嚴重制約了我國礦山企業(yè)的發(fā)展。因此，準確預測礦業(yè)安全生產事故對制訂合理的礦業(yè)安全決策，以及提高礦業(yè)安全管理水平具有重要的意義。

礦業(yè)安全系統(tǒng)是一個復雜的循環(huán)系統(tǒng)[2]，礦業(yè)安全生產受自然條件、作業(yè)環(huán)境等諸多因素影響[3]。目前，國內外眾多學者對礦業(yè)安全生產事故預測的方法展開了研究[4]。劉素兵等[5]將GM(1,1)與支持向量機融合，建立了灰色支持向量機組合預測模型；李懷俊等[6]通過參數尋優(yōu)改進了ARMA模型，提高了ARMA模型的預測精度；Barman等[7]通過螢火蟲算法(Firefly Algorithm，FA)優(yōu)化SVM的參數，提高了SVM模型的預測精度；劉俊娥等[8]提出了一種模糊信息粒化與SVM相結合的方法，對瓦斯涌出量進行了預測；JANG Y J等[9]使用長短期記憶(LSTM)遞歸神經網絡(RNN)的深度學習模型來預測業(yè)務失敗；WU Menglong等[10]對經驗模態(tài)分解后的序列單獨分析,建立預測模型來預測礦山安全生產形勢。然而上述方法預測效果的魯棒性較差，并且只能得到礦業(yè)安全生產事故的點預測結果，目前關于礦業(yè)安全區(qū)間預測的研究還較少。區(qū)間預測是一類既含有確定性又含有不確定性的預測[11]。為此，考慮將模糊信息粒化引入到礦業(yè)安全生產事故預測中，得到礦業(yè)安全生產事故時間序列的模糊區(qū)間預測結果。區(qū)間預測能夠提供對應某一期望概率的區(qū)間預測結果，獲取比確定性預測結果更多的信息，有利于決策者評估礦業(yè)安全生產事故的不確定性和風險因素，做出更為合理的決策[12]。因此，準確預測礦業(yè)安全生產態(tài)勢的變化趨勢和變化空間，在實際應用中具有重要的參考價值和指導意義。

筆者先將礦業(yè)安全生產態(tài)勢時間序列進行小波變換，然后采用樣本熵將子序列重組，將重組的分量按照一定窗口進行模糊信息粒化，得到能夠反映原始數據特點的信息粒；最后基于FCM對窗口化的 3個參數序列進行預測，以實現礦業(yè)安全生產事故時間序列的模糊區(qū)間預測。

1 模型的建立

通過小波變換和樣本熵(SE)算法將礦業(yè)安全生產事故的時間序列分解并重組，然后采用模糊信息粒化的方法，將礦業(yè)安全生產事故時間序列模糊粒化，得到Low、R、Up共3個粒化參數時間序列；最后依據模糊C均值聚類算法對窗口化的時間序列進行預測，建立礦業(yè)安全生產事故時間序列預測模型。

1.1 時間序列的分解與重組

原始時間序列x(t)的小波變換可以表示為[13]：

(1)

式中：s為伸縮因子；t為時間；τ為平移因子；φ*為小波基函數φs,τ的復共軛。

小波基基于以下2個原則確定：

1)能—熵比準則

將能量與熵結合起來形成一個新準則，即能—熵比準則[14]，見下式：

R(j)=Eenergy(j)/Eentropy(j)

(2)

式中：Eenergy(j)為原始時間序列在第j分解水平時小波系數序列包含的能量；Eentropy(j)為原始時間序列在第j分解水平時小波系數序列的Shannon熵。

由式(2)可以看出，能量越大，熵越小，則能—熵比越大，小波基[15]越優(yōu)。

2)相關性準則

在處理和分析時間序列時，相關性分析[16]是一種在時域中對序列特性進行描述的重要方法。

礦業(yè)安全生產事故時間序列的細節(jié)和近似部分可通過低通和高通濾波器獲得，通過對第(j-1)分解水平的近似系數與低通濾波器系數進行卷積，可以獲得第j分解水平的近似系數：

(3)

式中：aj,k為近似系數；dj,k為細節(jié)系數；h、g分別為所選取的小波函數對應的低通和高通濾波器的抽頭系數序列；m為維度；k=1,2,…,m。

經過小波變換后的時間序列具有一定重復性和復雜性，故采用樣本熵算法對各分量時間序列進行重組。

樣本熵的計算過程如下[17]：

1)將小波變換后的序列按序號形成n維的向量組Xm(1),…,Xm(N-m+1),其中Xm(i)={x(i),x(i+1),…,x(i-m+1)}，1≤i≤N-m+1。

(4)

3)定義B(m)(r)為：

(5)

4)將維數m增加至m+1維，對m+1維向量重復步驟1)～3)得到B(m+1)(r)。

5)該序列的樣本熵值為：

(6)

式中:m為重構維數,一般取m=2；r為相似容限，一般為原始數據標準差的0.10～0.25；n為數據長度。

1.2 重組序列的模糊信息粒化

根據一定的窗口w將原始時間序列分割成一些子序列。原始時間序列窗口以1個季度為1個單元，然后進行模糊信息粒化，得到窗口化后的3個粒化參數時間序列[18]。模糊信息粒化后模糊粒子的隸屬函數為[19]：

(7)

式中：x為論域中的變量；a、m、b為參數，對應窗口模糊化后得到的3個變量Low、R、Up；Low為窗口變化的最小值，R為窗口變化的平均值，Up為窗口變化的最大值。

1.3 基于FCM的窗口化序列模糊預測

基于FCM對窗口化的時間序列進行預測，FCM的建模過程如下[20]：

1)確定聚類中心數。設原始礦業(yè)安全生產事故時間序列為Xt，t=1，2，…，N；待預測值為XN+1。首先對原始序列進行聚類，通過下式確定原始序列的聚類中心數：

(8)

式中：c為聚類中心數；Xmax、Xmin為原始序列中的最大值和最小值；[]為取整運算。

2)初始化聚類中心。根據式(8)計算得到聚類中心數，隨機選定初始聚類中心Ck。Ck是一個長度為c的向量，k=1，2…，c。

3)計算目標化函數。FCM的目標化函數為：

(9)

式中：Ck為模糊組i的聚類中心；uij為屬于第i個聚類的隸屬度，介于0～1；dij為第i個聚類中心與第j個數據點間的歐幾里得距離。

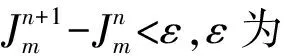
2 模型應用

以2005—2019年礦業(yè)單位從業(yè)人員事故的萬人死亡率為研究對象,統(tǒng)計得到全國礦業(yè)事故萬人死亡率時間序列,如圖1所示。

圖1 2005—2019年全國礦業(yè)事故萬人死亡率時間序列

2.1 小波變換

采用能—熵比準則及相關性準則選取最優(yōu)小波基，并依據相關性準則確定臨界分解水平。

筆者采用較為常用的dbN(1～10)、coifN(1～5)、symN(2～10)3種小波系選取最優(yōu)小波基。

2.1.1 能—熵比準則的計算結果

基于能—熵比準則的計算結果如表1所示。

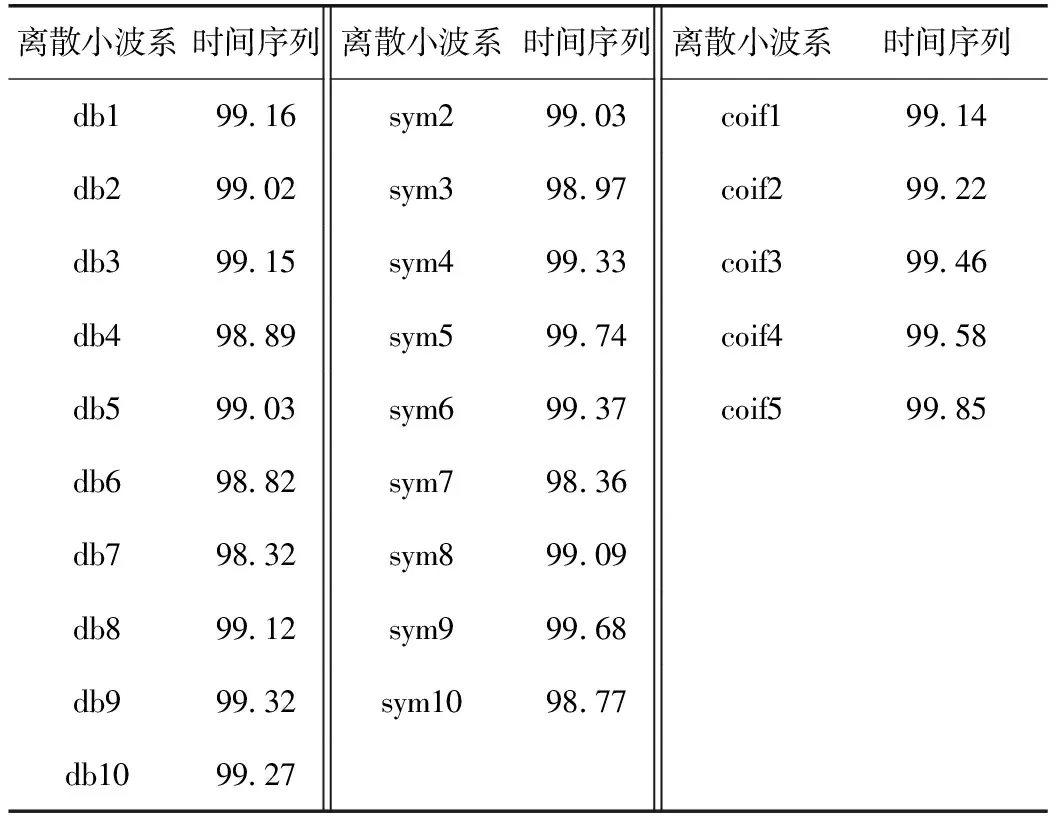
表1 基于能—熵比準則R(j)的計算結果

將表1中數據依據時間序列比值高低排序，結果如表2所示。

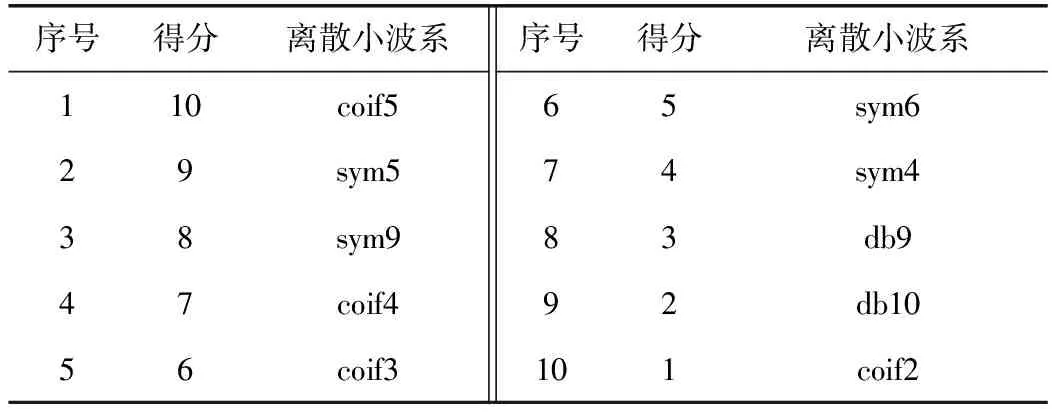
表2 基于能—熵比準則R(j)對小波基的排序

2.1.2 相關性準則的計算結果

基于相關性準則的計算結果如表3所示。

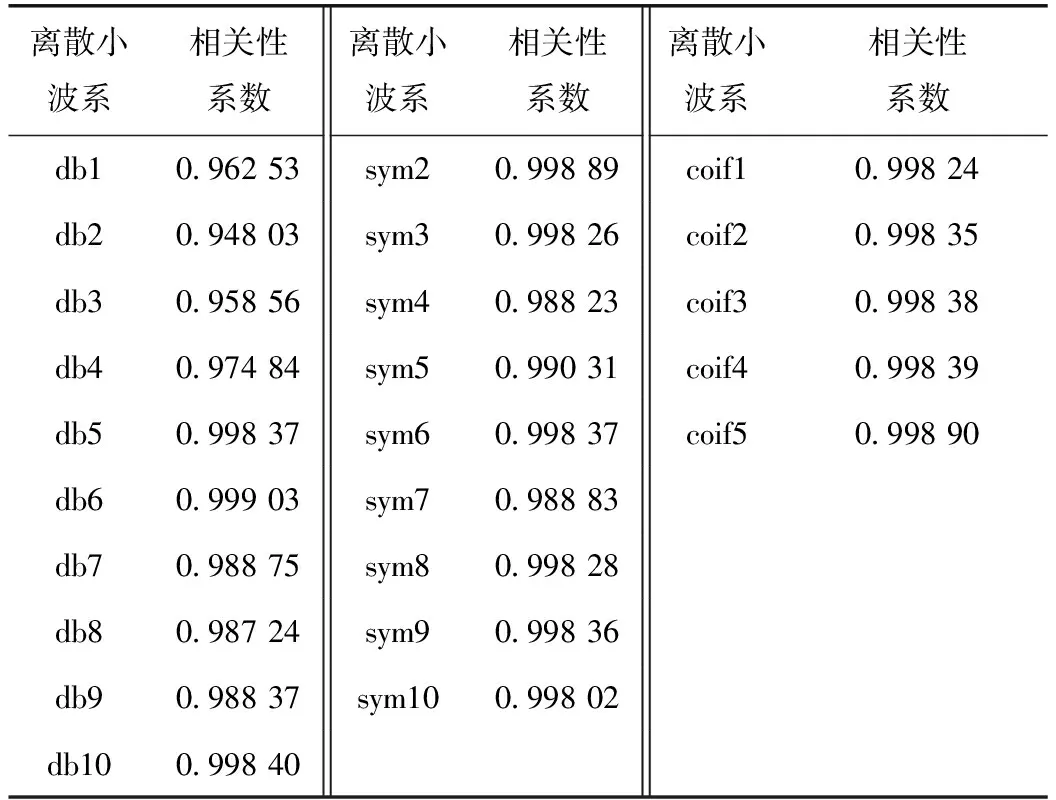
表3 基于相關性準則的計算結果

將表3中數據依據相關性系數大小進行排序，排序結果如表4所示。

表4 基于相關性準則對小波基的排序結果

2.1.3 小波基優(yōu)選結果

計算表2、表4中小波基的得分，根據其對應的分值進行排序，排序結果如表5所示。

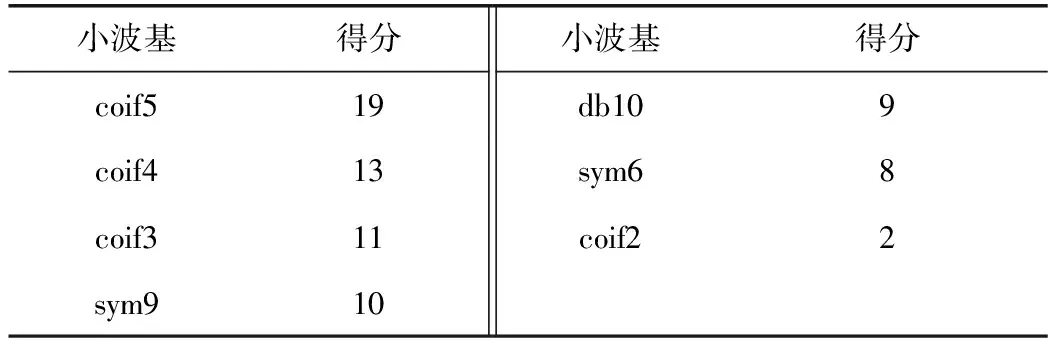
表5 小波基排序結果

由表5可知，小波基coif5得分最高，coif5為最優(yōu)小波基。

2.1.4 臨界分解水平的確定

基于臨界分解水平判別準則，對曲線的臨界分解水平進行分析判斷,得到各分解水平趨勢序列與原始礦業(yè)安全生產事故時間序列的相關性系數,結果如圖2所示。

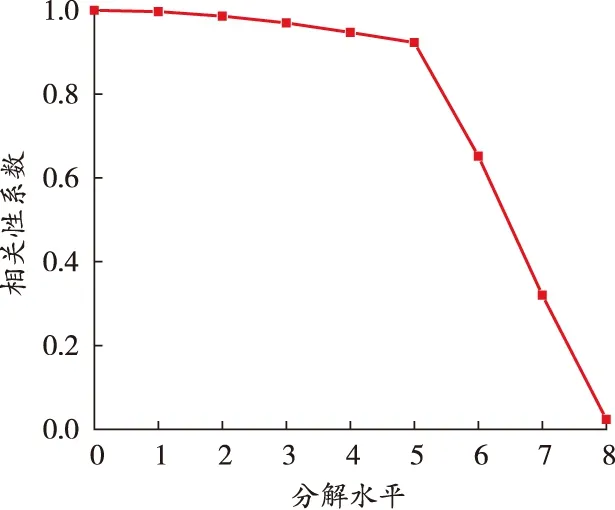
圖2 各分解水平的相關性系數

由圖2可知，礦業(yè)安全生產事故時間序列曲線分解水平大于5時，相關性系數發(fā)生顯著變化，故確定臨界分解水平為5。

2.1.5 時間序列的分解

在確定最優(yōu)小波基和臨界分解水平后，利用MATLAB小波工具箱對其進行小波變換。礦業(yè)安全生產事故時間序列5分解水平小波變換后的結果如圖3所示(圖中S代表原始序列，ai代表近似部分，di代表細節(jié)部分)。

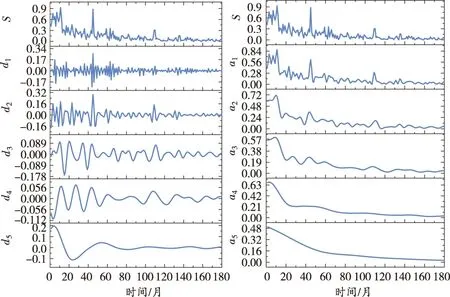
(a)細節(jié)部分 (b)近似部分

由圖3可知，隨著分解水平的增加，細節(jié)部分逐漸被提取出來。經過5分解水平小波變換后，可以滿足礦業(yè)安全生產事故時間序列分解的要求。

2.2 分量重組

基于礦業(yè)安全生產事故時間序列進行小波變換后的子序列，計算給定序列與子序列的樣本熵值，各分量的樣本熵如圖4所示。

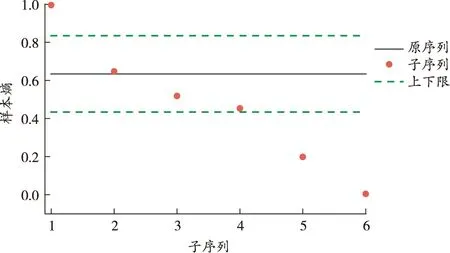
圖4 各分量的樣本熵

根據子序列樣本熵的分布情況，取λ=0.2。d1為隨機分量；d2～d4重組為細節(jié)分量s；d5、a5重組為趨勢分量r。重組后各分量結果如圖5所示。

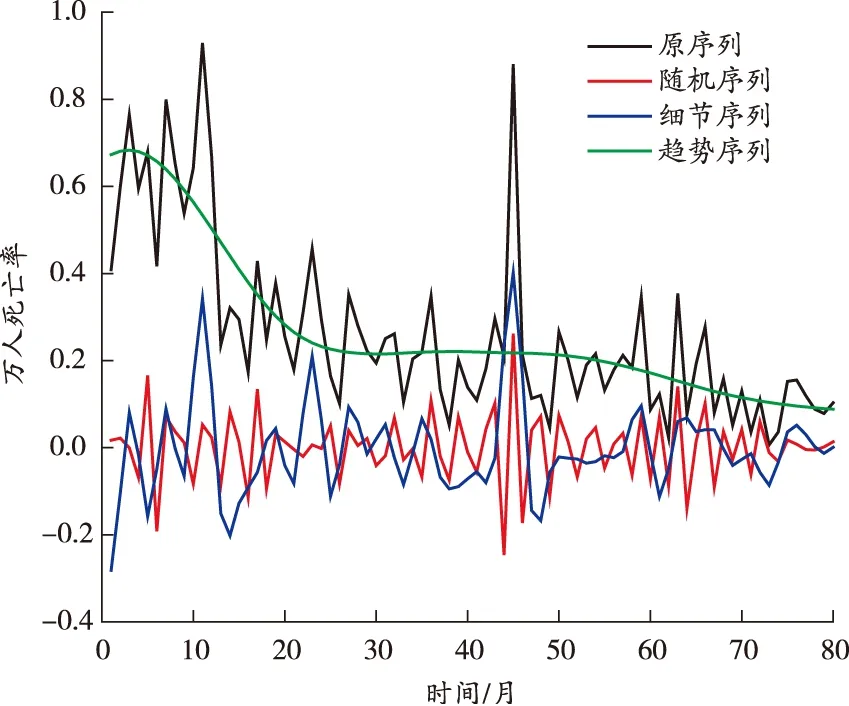
圖5 重組后各分量

2.3 重組分量的信息粒化

由圖5可知，樣本熵重組后的序列具有隨機性、波動性等特點。為此，先將原始數據按照一定窗口進行模糊信息粒化，將礦業(yè)安全生產態(tài)勢時間序列的萬人死亡率模糊信息粒化為Low、R、Up共3個參數，3個子序列的模糊信息粒化結果如圖6所示。該例中Low具體為窗口化子序列每月變化的最小值，R具體為礦業(yè)安全生產態(tài)勢萬人死亡率每月變化的平均值，Up具體為礦業(yè)安全生產態(tài)勢萬人死亡率每月變化的最大值。

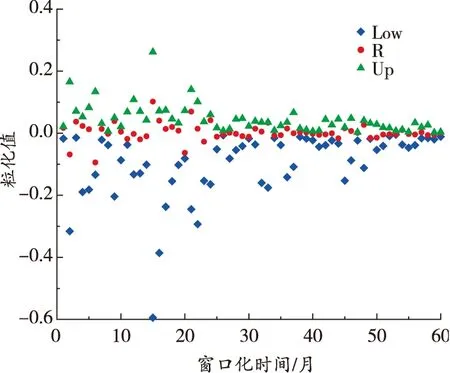
(a)d2序列粒化

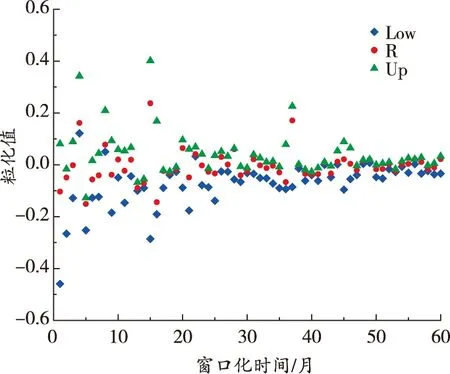
(b)d3序列粒化

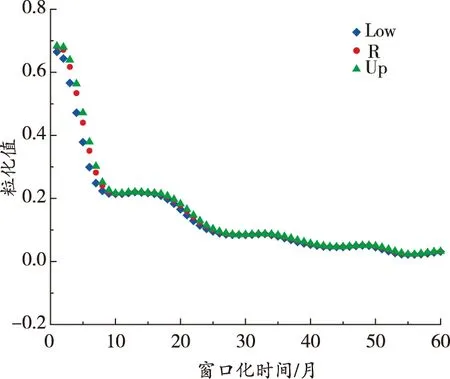
(c)d4序列粒化

2.4 基于FCM的窗口化子序列模糊預測

對于窗口化的時間序列，按照窗口模糊信息粒化結果將其分成6個數據集，根據每年數據情況確定討論區(qū)間的上下界計算模型的論域。基于樣本數據求得的隸屬度值見表6，樣本模糊化后的結果如表7 所示。

表6 樣本隸屬度

表7 樣本模糊關系

由表6和表7并結合式(9)計算，求得測試集預測結果，如表8所示。

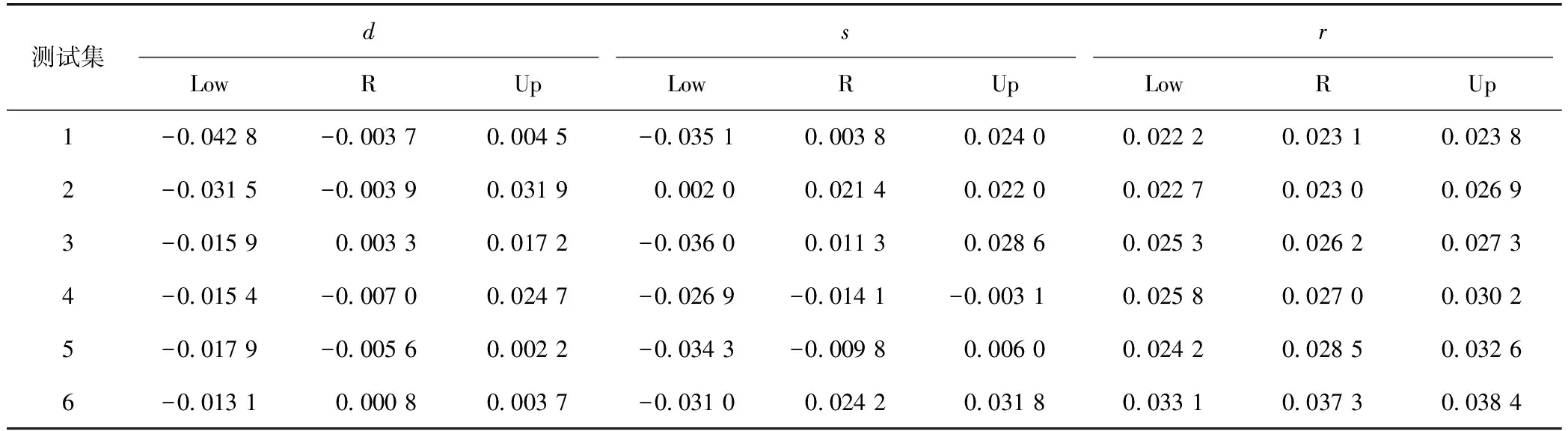
表8 測試集預測結果

合并窗口化后，礦業(yè)安全生產事故時間序列的模糊區(qū)間預測結果如圖7所示。

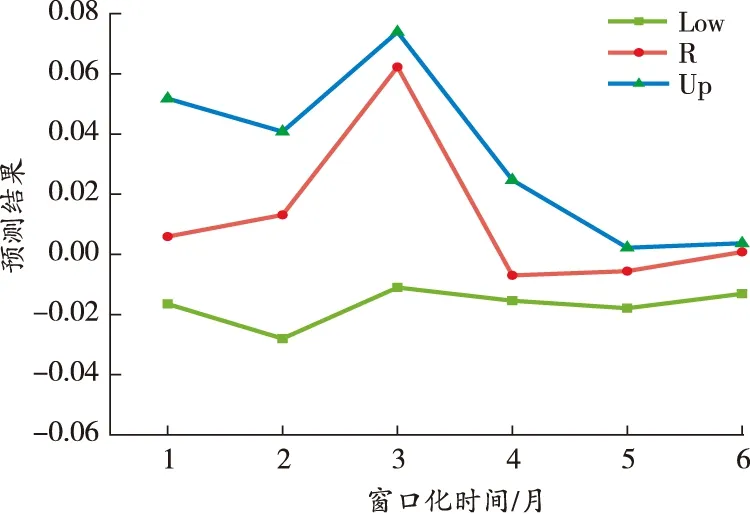
圖7 窗口化區(qū)間預測結果

3 模型的驗證

利用訓練集150組樣本建立的模型，對2018年7月至2019年10月測試集的21組數據進行預測，并計算區(qū)間上下邊界值與中值的預測值，結果如表9 所示。

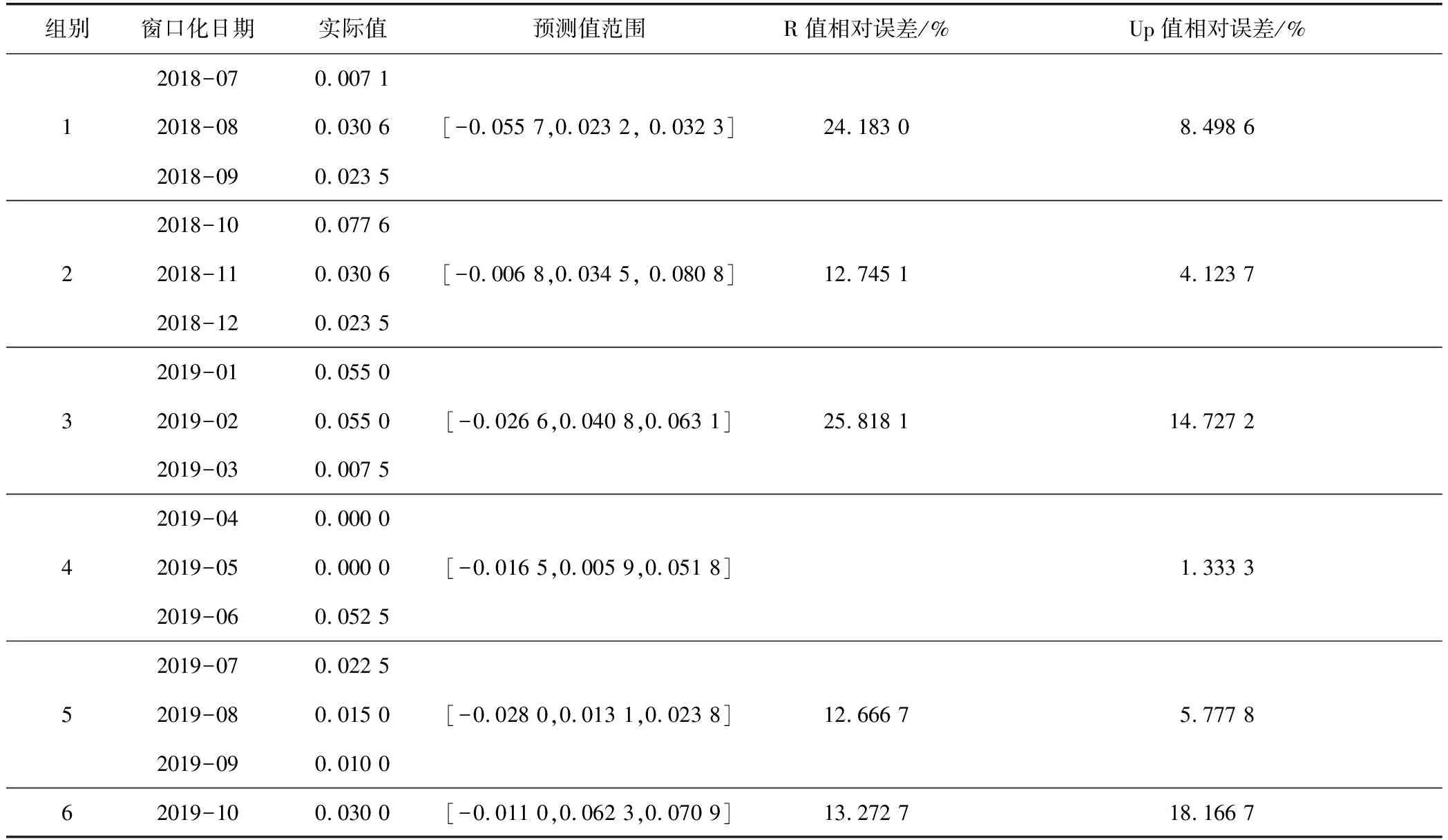
表9 測試集預測誤差對比

由表9可知：R值的平均相對誤差為17.737 1%，Up值的平均相對誤差為8.771 2%。Up值的預測精度明顯高于R值的預測精度，表明模糊信息粒化后的上下邊界值能夠較為準確地描述礦業(yè)安全生產事故的變化范圍。

將礦業(yè)安全生產事故時間序列的模糊區(qū)間預測模型與小波-SVM(支持向量機)、小波-ARMA(自回歸滑動平均模型)和小波神經網絡的預測效果進行對比，各模型的預測誤差分析如表10所示。其中，MAE為預測值和實際值之間的平均絕對誤差；MRE為絕對誤差與真實值的比率，即平均相對誤差；RMSE為均方根誤差，其對異常值更為敏感。

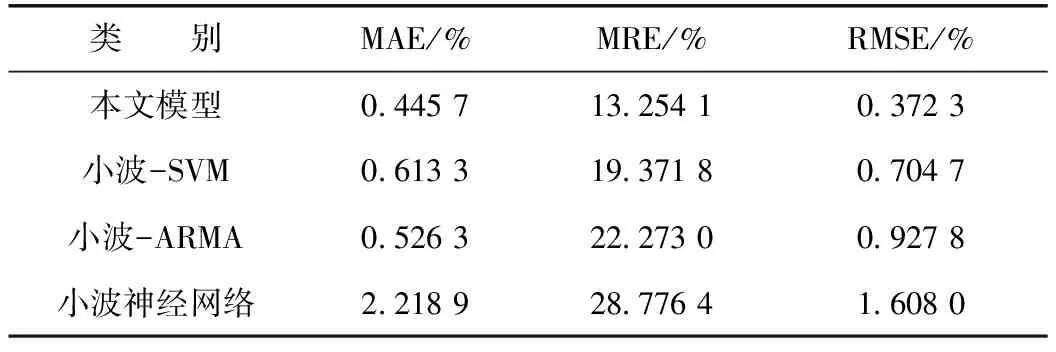
表10 各模型預測誤差對比分析結果

由表10可知，本文預測模型的MAE、MRE、RMSE分別為0.445 7%、13.254 1%、0.372 3%，各項指標均低于對比模型，表明本文模型預測效果較為穩(wěn)定，精度較高。

4 結論

1)提出一種礦業(yè)安全生產事故時間序列的模糊區(qū)間預測模型，能夠將礦業(yè)系統(tǒng)中的隨機因素等考慮進去，相較于定量值的點預測，區(qū)間預測的結果更為可靠，更具有實用價值。

2)R、Up值時間序列預測的平均相對誤差分別為17.737 1%、8.771 2%。邊界值的預測精度較高，表明模型的區(qū)間范圍較為可靠，也進一步地說明了模糊信息粒化后的邊界值結果的合理性。

3)相對于小波-支持向量機、小波-自回歸滑動平均模型和小波神經網絡的預測結果，本文的預測模型平均絕對誤差(MAE)、平均相對誤差(MRE)、均方根誤差(RMSE)3個指標均為最小，表明訓練得到的模型具有較高的可靠性，對礦業(yè)安全決策具有一定的指導意義。