基于虛擬同步發電機的慣量和阻尼自適應控制

孫宇新，王鵬，施凱，徐培鳳

（江蘇大學電氣信息工程學院，江蘇 鎮江 212013）

伴隨著工業革命的大浪潮，傳統能源短缺問題成為我們急需面對的大挑戰，與此同時，清潔無污染的可再生能源成為很好的替代品，于是以微電網為主的分布式電源的應用也越來越廣泛[1-2]。傳統的電力系統通常采用同步發電機作為主要電源，可以利用其轉子的慣性，通過釋放轉子動能來維持系統穩定。由于大部分分布式電源不能直接并入電網使用，一般都需要用并網逆變器作為接口，但是傳統的并網逆變器過載能力比較差，輸出阻抗和慣性也都比較小[3-4]。為此，國內外學者提出采用VSG技術，通過改進控制方法模擬同步發電機（SG）的外特性，為電網提供慣性和阻尼，從而提高了逆變器抑制自身頻率輸出和功率波動的能力，增強系統的穩定性。

文獻[5]提出了一種自適應旋轉慣量的控制方法，通過在新的慣量控制環節加入低通濾波單元，抑制系統負荷變化造成的頻率迅速波動，但是并未說明低通濾波單元的參數選取原則，且沒有分析VSG并網功率發生擾動時系統的穩定性。文獻[6]通過在功率側加入由功率變化量和變化率的結合得到的輔助功率，從而實現強化慣量的控制，從結果可以看到系統的頻率偏差明顯得到改善，但是頻率的變化率并未發生變化，且功率的偏差幅值變大。文獻[7-8]都提出了一種自適應慣量的控制方式，分別構造了角速度變化率與虛擬慣性的關系，但是在拐點處角速度的變化率非常大，可能造成系統失穩，且忽略了阻尼的自適應作用。文獻[9]提出了一種慣量阻尼自適應的控制策略，實現了慣量和阻尼的自適應交錯控制，但是其控制策略設計的參數較多，且并未說明參數的確定原則。

針對以上問題，本文提出了一種自適應虛擬慣量和阻尼的協同控制策略，建立了虛擬轉動慣量、阻尼系數與系統頻率偏差量、頻率變化率的關系，當系統發生功率擾動時，虛擬轉動慣量和阻尼系數的大小會根據系統頻率的偏差量和變化率而進行自適應地變化，從而有效減小了系統的超調，縮短了系統的暫態過程，提高了系統的穩定性。并通過仿真分析對控制系統中的自適應控制參數進行了確定。

1 VSG的基本原理

圖1所示為VSG的結構模型與控制模型，其中結構模型中左側的直流電壓源代表微電網的電源，逆變控制系統等效替代同步發電機的作用。

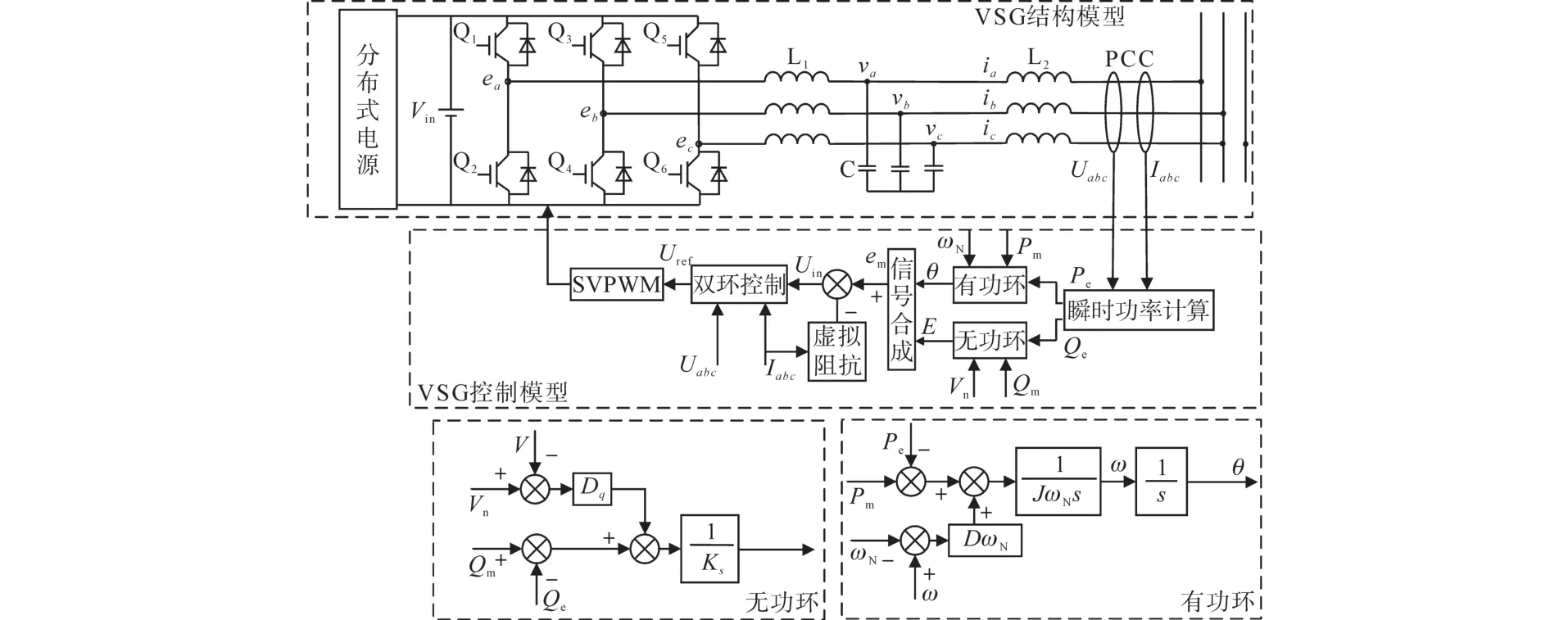
圖1 虛擬同步發電機結構Fig.1 Structure of VSG

通常情況下，為了方便分析，假設同步發電機的極對數為1，則同步發電機的機械角速度與電氣角速度相等。根據傳統SG的二階模型，等效的轉子運動方程如下式所示：

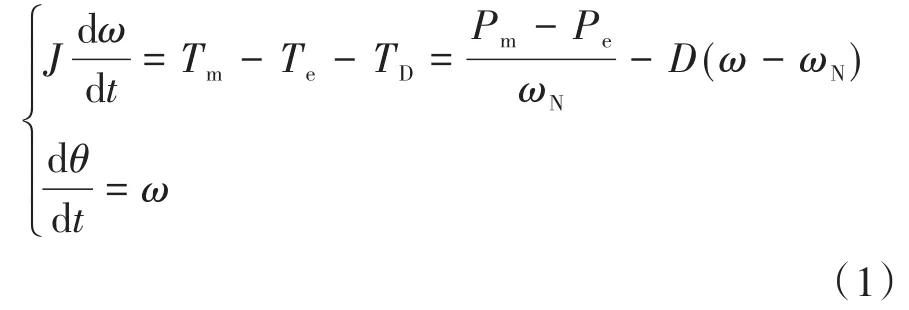
式中：J為同步發電機的轉動慣量；D為阻尼轉矩對應的同步發電機的阻尼系數；Tm，Te，TD分別為同步發電機的機械轉矩、電磁轉矩和阻尼轉矩；θ等效為同步發電機的功角；ω，ωN分別為同步發電機的系統輸出角速度和額定角速度，ωN等效為電網同步角速度；Pm，Pe分別為機械功率和電磁功率。

式（1）模擬了同步發電機的本體特性，VSG通過引入虛擬轉動慣量J和阻尼系數D模擬SG的轉子慣性和阻尼，這對于整個微網系統的頻率穩定性具有非常大的改善作用。同時根據式（1）可以得到VSG的有功環，如圖1中VSG的控制模型所示。

如圖1中無功環所示，得到VSG控制的電壓-無功控制環節如下式：

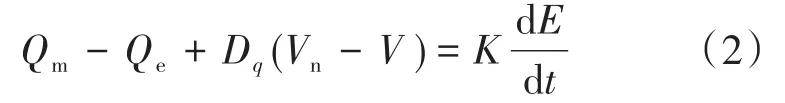
式中：Qm為參考無功功率；Qe為VSG輸出無功功率；Dq為無功調節系數；K為積分系數；V為系統輸出電壓幅值；Vn為系統額定電壓幅值；E為逆變器輸出電壓基波分量幅值。

2 自適應虛擬轉動慣量和阻尼系數控制

2.1 轉動慣量和阻尼系數對VSG的特性影響

本文研究的VSG控制均是在并網狀態下進行的，因此忽略內環控制延時后，有功控制回路可以簡化為如圖2所示。其中，KP為簡化的同步功率，大小為EU/Z，Z為VSG的虛擬阻抗、線路阻抗等其他零散阻抗之和。本文中為了便于分析，假設KP為固定的已知量。

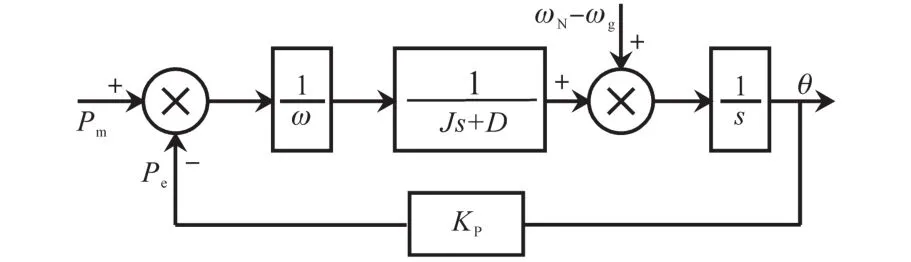
圖2 并網運行下的有功控制結構Fig.2 Structure of P control loop in grid-connected mode

由圖2可以得到并網時有功控制回路的開環傳遞函數和閉環傳遞函數分別為

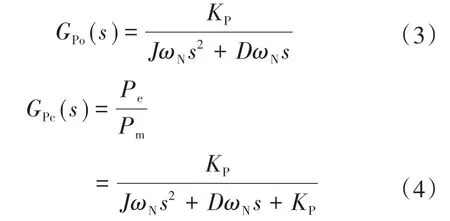
可以發現，有功回路對應的閉環傳遞函數為一個典型的二階模型，則可以得到二階模型對應的自然振蕩角頻率ωn和阻尼比ξ分別為

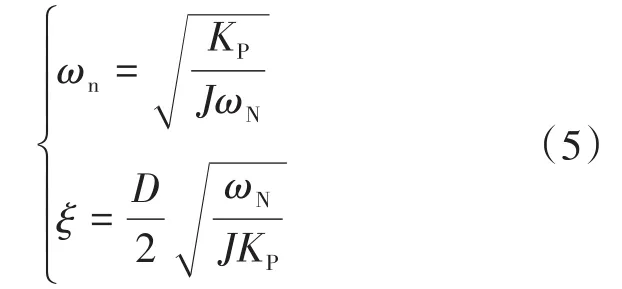
假設取0＜ξ＜1，誤差帶為±5%，則此二階系統對應的最大超調量σ%和調節時間ts分別為

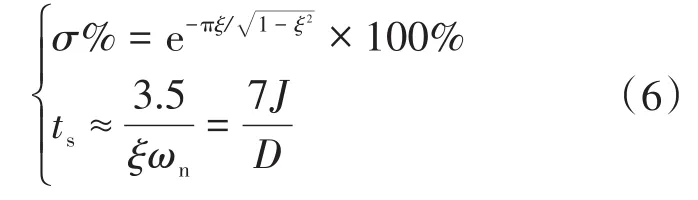
從式（6）可以得到，在有功功率以及無功功率都給定時，有功環對應的二階模型的動態性能由轉動慣量J和阻尼系數D來決定。其中慣量J主要對頻率的變化率有較大的影響，阻尼D對頻率的偏差量有較大的影響。

2.2 自適應控制原理

當VSG在并網條件下發生功率擾動時，功率與系統頻率都會在擾動的瞬間出現衰減震蕩，而震蕩的超調量與趨于穩定的時間是評判系統穩定性的關鍵參數。如圖3所示，當VSG的給定有功功率由P1突增為P2時，整個系統的穩定運行點也從A點切換到B點，在這個過程中，系統功率和頻率變化均為衰減震蕩。

圖3 虛擬同步發電機的功角和角速度曲線Fig.3 Power angle curves and angular velocity curves of VSG

為便于進行分析，在轉動慣量和阻尼均為固定值時，將衰減振蕩的過程分為4個部分：①t1—t2；②t2—t3；③t3—t4；④t4—t5。如圖 3 所示，在區間①內，發生擾動瞬間，頻率會發生突增，即VSG的角速度大于電網的角速度，如圖3d所示，且會持續增加，即角速度的變化率 dω/dt＞0，因此，此時應增大虛擬轉動慣量J與阻尼系數D來抑制角速度的超調幅值以及角速度的變化率。此時Δω（dω/dt）＞0；在區間②內，轉子角速度依然大于電網角速度，即Δω＞0，但是角速度處于減速階段，轉子角速度的變化率dω/dt＜0，因此應適當減小轉動慣量，使角速度加速恢復到額定值；當轉動慣量J不變時，阻尼D的增大同時會使dω/dt減小，因此應適當減小阻尼D，避免由于過大的阻尼D抵消轉動慣量J的作用。此時Δω（dω/dt）＜0；區間③、區間④與區間①、區間②原理類似，不再詳細分析。當系統恢復正常，功率從P2恢復到P1時，系統穩定點從B點切換到A點，其整個過程與上述分析一致，不再贅述。

根據分析結果可以得到表1所示的自適應虛擬慣量和阻尼系數的選取原則表。

表1 虛擬慣量和阻尼系數選取原則Tab.1 Selecting principle of J and D

由于ω=2πf，所以 Δω，dω/dt，Δω（dω/dt）的正負變化與 Δf，df/dt，Δf（df/dt）一致，因此根據表1所示的虛擬轉動慣量與阻尼系數的選取原則，可以得到自適應控制策略為

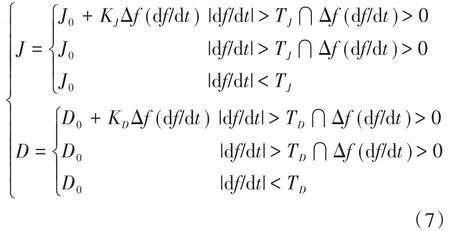
式中：J0，D0分別為VSG穩定運行時的轉動慣量和阻尼系數；KJ，KD分別為轉動慣量和阻尼的調節系數；TJ，TD分別為頻率的偏差速率閾值和頻率偏差閾值。

根據表1和式（7）可以得到自適應控制原理圖如圖4所示。在區間①內慣量增大后值為J0+KJ|Δf（df/dt）|；阻尼系數增大為D0+KD|Δf（df/dt）|；在區間②內轉動慣量應適當減小，恢復到恒定慣量J0即可，阻尼系數也適當減小，恢復到D0，使頻率快速減小到穩定值；在區間③、區間④內，慣量和阻尼的變化情況與區間①、區間②類似。

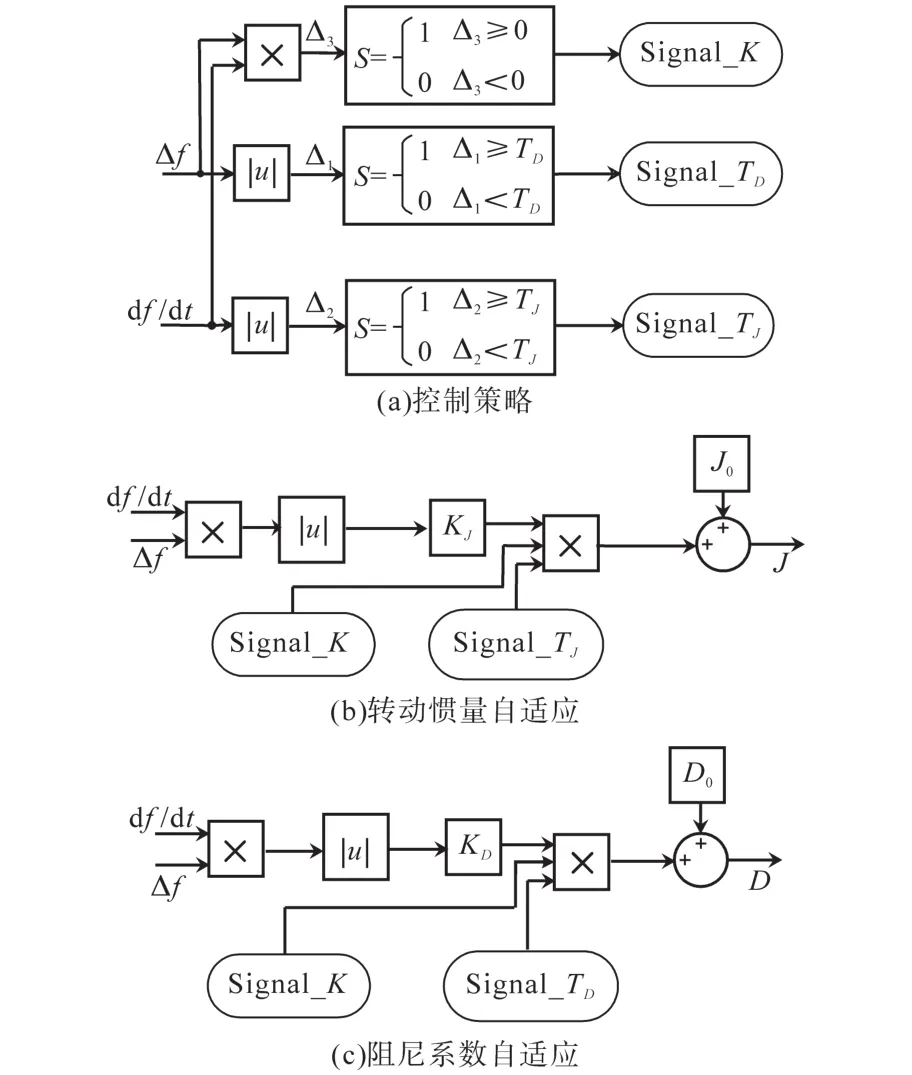
圖4 自適應控制原理圖Fig.4 Adaptive control schematic

3 參數整定

一般情況下，VSG穩定運行時的轉動慣量J0和阻尼系數D0都按照“最優二階系統”的方法整定，使系統能夠獲得較快的響應速度和較小的超調量。

3.1 確定參數KJ和KD

根據第2節有功環傳遞函數式（3）、式（4）可以得到不同轉動慣量J和阻尼系數D下有功環的根軌跡簇如圖5所示。

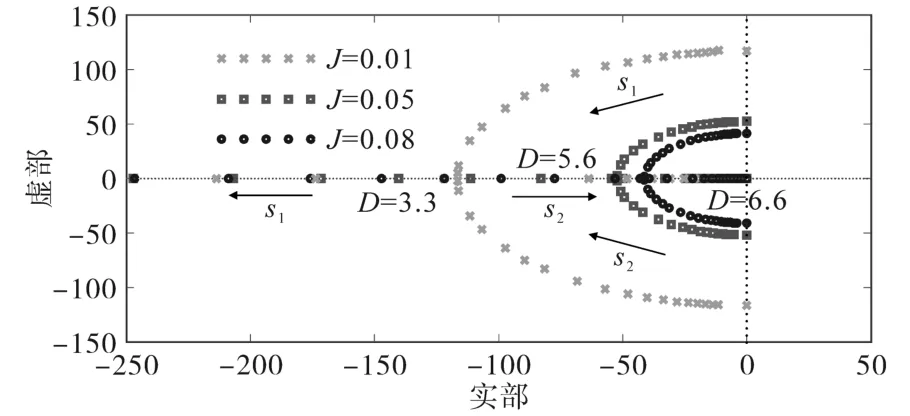
圖5 不同J和D下有功環的根軌跡Fig.5 Root locus with different J and D

從圖5中可以看到，當J分別為0.01，0.05和0.08時，D從0增大到無限大的根軌跡。s1和s2是系統的一對共軛復根，按照圖中箭頭所示的方向運動，同時也是D從0緩慢增加的方向。可以發現，隨著D的增大，s1和s2同時向復平面的左側移動，說明此時系統的動態性能較好，系統處于欠阻尼狀態，為衰減振蕩，有一定的超調；但隨著D的繼續增大，s1和s2逐漸在實軸上會合，虛部變為0，此時對應的是系統的臨界阻尼狀態；如果D繼續增大，s1和s2都將在實軸上沿相反方向運動，此時系統處于過阻尼狀態，會造成系統的調節時間增加，因此阻尼系數D不能過大。另外一方面，從圖中可以發現，隨著J的增長，特征根s1和s2的分離點逐漸趨于0，即逐漸向虛軸移動，造成系統的響應速度變慢，因此轉動慣量J也不能太大[10]。

文獻[4]推導了慣量J和D之間的約束方程，并給出了J和D的選取范圍。因此本文所提出的控制策略的自適應慣量和阻尼都應滿足文獻[4]中的參數選取范圍，即可得Jmax，Dmax。

由式（7）可知慣量和阻尼調節系數范圍為

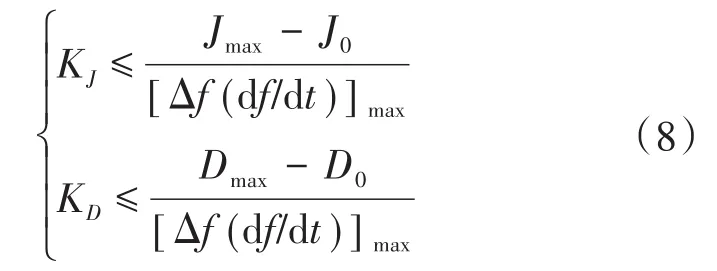
代入數據可得KJ≤0.75，KD≤3.05，具體的調節參數大小通過仿真結果進行進一步的確定。

圖6為系統發生功率擾動時的頻率變化曲線。在對慣量和阻尼調節系數進行整定時，首先調節KD=0，分別選取KJ為0.25，0.50，0.75和1.00，系統發生功率擾動時的頻率變化曲線如圖6a所示。從圖6a中可以發現，隨著KJ的增大，頻率的變化速度明顯變緩，但是穩定時間卻變長了，且當KJ=1.00，即超過確定范圍時變化尤為明顯；然后調節KJ=0，分別選取KD為1，2，3和4，系統發生功率擾動時頻率變化曲線如圖6b所示，從圖6b中可以看到，頻率的振蕩幅值得到了明顯的降低，但是當其調節參數超過確定范圍時，震蕩的周期變長了。因此分別根據其控制效果，按照取中的原則進行參數的確定。

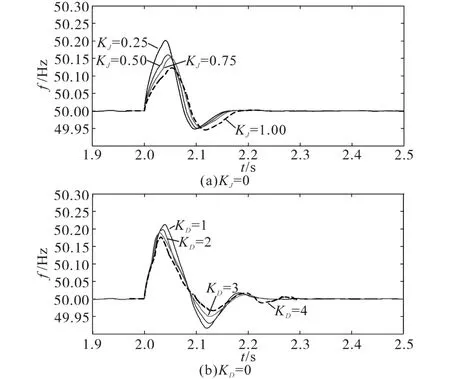
圖6 調節KJ及KD時系統頻率變化曲線Fig.6 System frequency change curves when adjusting KJand KD

3.2 確定參數TJ，TD

VSG正常運行時，系統的頻率會有較小的波動，但是頻率的變化率并不能夠忽略不計。TJ作為頻率的偏差速率閥值，用來判斷是否進行自適應慣量的切換開關，為避免正常運行時的誤操作，TJ一定要大于VSG正常運行時頻率偏差速率的最大值，同時為了提高自適應系統的精度，TJ也不能太大，因此只需要滿足避免誤操作即可。頻率的偏差閾值TD同理可得。

4 仿真實驗

為驗證本文所提控制算法的正確性和有效性，本文在Matlab/Simulink仿真軟件平臺搭建了單臺VSG并網的仿真模型。仿真系統的主要參數如下：直流側電壓Vin=800 V，電網電壓Ug=220 V，額定頻率fN=50 Hz，濾波電感L1=4 mH，網側電感L2=0.8 mH，濾波電容C=10 μF，開關頻率fK=10 kHz，J=0.07 kg·m2，D=4.62 N·m·s·rad-1，KD=2，KJ=0.5，TJ=2.5，TD=0.015。

本次仿真的模型為：VSG先進行預同步，在1.5 s左右進行并網后，分析有功功率發生擾動時系統的穩定性，仿真時長為3 s，其中2 s以前VSG給定輸出有功功率都為10 kW，在2 s時有功功率突增為14 kW，在2.5 s又恢復為10 kW。

圖7為不同控制策略下VSG的輸出有功功率變化曲線。VSG在并網狀態下，在2 s功率由10 kW突增為14 kW，此時功率會發生超調。傳統慣量阻尼控制、自適應慣量控制與自適應慣量和阻尼協調控制的有功功率超調量分別為14.28%，10.86%和3.28%；再次恢復穩定所需時間分別為0.22 s，0.20 s和0.14 s。在第2.5 s功率恢復到10 kW時，同樣可以看到自適應慣量和阻尼協調控制的有功功率振蕩幅值和調節時間明顯減小。因此可以得到結論：當功率發生擾動時，自適應慣量和阻尼控制可以有效抑制功率的振蕩。

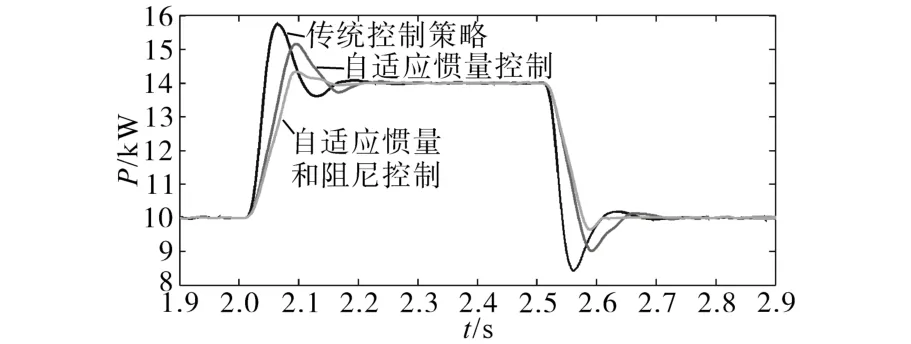
圖7 虛擬同步發電機的有功功率變化曲線Fig.7 Active power curves of VSG

圖8為不同控制策略下VSG輸出頻率的變化曲線對比。在第2 s功率發生突增后，傳統慣量阻尼控制、自適應慣量控制與自適應慣量和阻尼控制的輸出頻率偏差分別為0.34 Hz，0.18 Hz和0.09 Hz。可以看到，自適應慣量控制能夠有效地抑制頻率的變換速度，減小超調范圍，但在加入阻尼的自適應控制后，進一步減小了頻率的偏差范圍，并縮短了調節時間，完全滿足國家的要求標準。

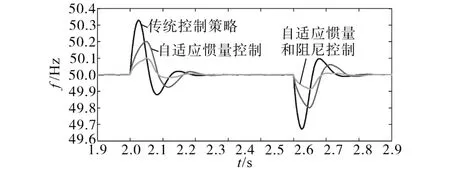
圖8 虛擬同步發電機的頻率震蕩曲線Fig.8 Frequency oscillation curves of VSG

圖9所示為VSG發生擾動后的虛擬轉動慣量和阻尼系數變化大小，由于頻率變化拐點處的df/dt變化較大，造成慣量和阻尼都在2.04 s左右有一個突刺，但都在系統穩定允許的范圍內。

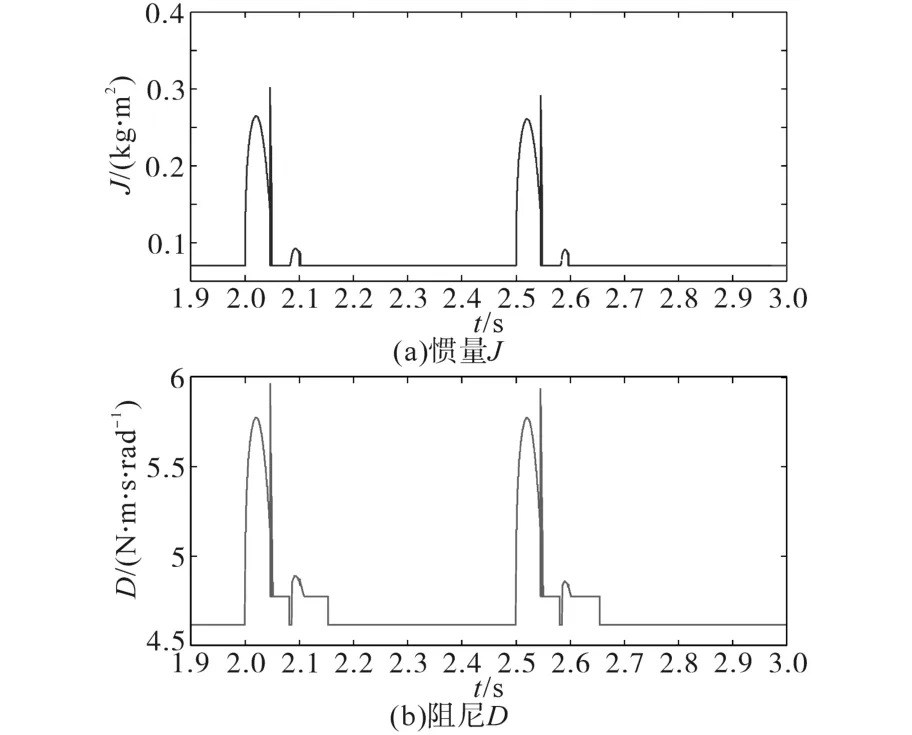
圖9 VSG的慣量和阻尼變化曲線Fig.9 The variation curves of VSG parameters J and D

圖10所示為VSG在不同控制策略下的輸出電流波形對比，其中，圖10b為圖10a中虛線框部分的局部放大圖。可以看到，當系統功率發生突變或者驟降時，傳統控制的VSG輸出電流也都會發生突增或者驟降，而本文提出的自適應控制策略能夠有效地抑制電流的突增和驟降，使其平穩地過渡。

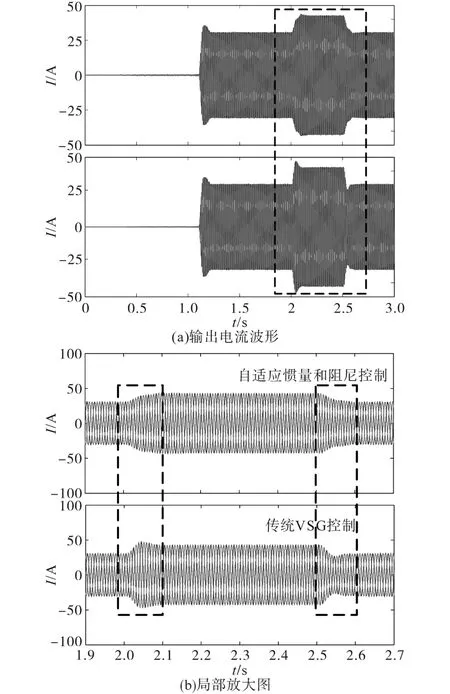
圖10 不同控制時電流對比Fig.10 Comparation of current among different control modes

5 結論

針對分布式電源大量并網時由于功率擾動帶來的穩定性問題，本文提出了一種新型的自適應虛擬慣量和阻尼控制策略，得到以下結論：

1）結合轉動慣量和阻尼系數分別對系統穩定性的影響，并通過分析VSG的功角和角速度變化曲線，最終得到自適應慣量和阻尼的控制方案。

2）通過對仿真得到的波形圖進行分析后可以得到結論：與傳統的VSG控制方案相比，本文所提出的自適應控制策略不僅可以抑制頻率的變化速度，還能夠降低頻率的偏差量。

3）本文只對單臺VSG的功率擾動情況進行了研究，并未研究多臺VSG并聯時的情況，這也正是課題組接下來研究方向的重心。