基于ZVS負載范圍的移相全橋變換器參數優化設計

何俊鵬，張潤澤，白旭峰，郝帥，曹虎

（中車青島四方車輛研究所有限公司技術中心，山東 青島 266000）

移相全橋變換器由于其超前和滯后臂的IGBT可實現零電壓開通（zero-voltage-switch，ZVS），使其降低了開關管的導通損耗，提高了開關頻率，減小了系統的體積和重量，提高了系統的轉換效率[1-6]。因此，移相全橋ZVS變換器被廣泛的應用于直流電源中。

然而在實際工程應用中，移相全橋ZVS變換器的參數設計卻存在很大的困難。移相全橋參數設計的不合理將會導致ZVS軟開關負載范圍窄、工作效率低、占空比丟失嚴重等一系列問題，這都將影響系統的整體性能。因此，移相全橋ZVS變換器關鍵參數的優化設計十分重要。

目前國內外大部分學者更多的是側重于研究移相全橋ZVS變換器的電路拓撲以改善其本身的缺陷，但針對其復雜的參數設計，大部分文獻并沒有系統地研究與分析[7-15]。文獻[7]和文獻[8]均是通過增加輔助諧振網絡，使變換器的滯后臂可以實現更寬范圍的ZVS。文獻[9]提出了一種用耦合電感實現零電壓零電流開關的移相全橋變換器，通過一個雙繞組的耦合電感和兩個二極管實現滯后臂開關管在寬負載范圍的零電流關斷。文獻[11]提出了一種輔助電流可控的移相全橋零電壓開關PWM變換器，可以在寬電壓輸入和全負載范圍內實現一次側開關管的ZVS。文獻[13]和文獻[14]在主電路拓撲結構上增加了一個磁芯，拓寬了變換器零電壓軟開關的實現范圍，大大提高了輕載狀況下的電源效率。這類方法既增加了電路的復雜性，同時也降低了系統可靠性。文獻[15]針對移相全橋ZVS變換器，介紹了其工作原理并詳細設計了諧振主電路關鍵元件參數，但是并沒有定量分析諧振電感、IGBT死區時間等影響滯后臂ZVS的關鍵參數。

本文通過深入分析移相全橋ZVS變換器工作原理，推導出系統占空比丟失以及ZVS負載范圍的數學表達式，并提出了一種基于ZVS負載范圍的移相全橋變換器的參數優化設計方法。該方法將對移相全橋電路的設計具有十分重要的指導意義。

本文第1部分介紹移相全橋ZVS變換器的工作原理；第2部分基于ZVS負載范圍，針對其關鍵參數進行優化設計，詳細地介紹隔直電容、輸出濾波電感、諧振電感以及IGBT死區時間的設計方法；第3部分通過搭建實驗樣機驗證理論分析的正確性；最后對全文做出總結。

1 移相全橋ZVS變換器工作原理

圖1為移相全橋ZVS變換器主電路結構圖，其中，Q1～Q4為4個開關管，D1～D4和C1～C4分別為4個開關管的寄生二極管和寄生電容。Lr為諧振電感，Cb為隔直電容，Da～Dd為整流二極管，Lo和 Co分別為輸出濾波電感和濾波電容。同一橋臂的兩個開關管以180°互補導通，這里稱Q1，Q3為超前臂，Q2，Q4為滯后臂。圖2為移相全橋ZVS變換器的主要波形圖。

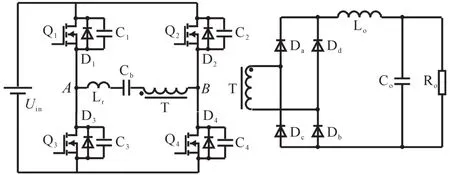
圖1 移相全橋ZVS變換器主電路結構圖Fig.1 Main circuit structure of phase-shifted full-bridge ZVS converter

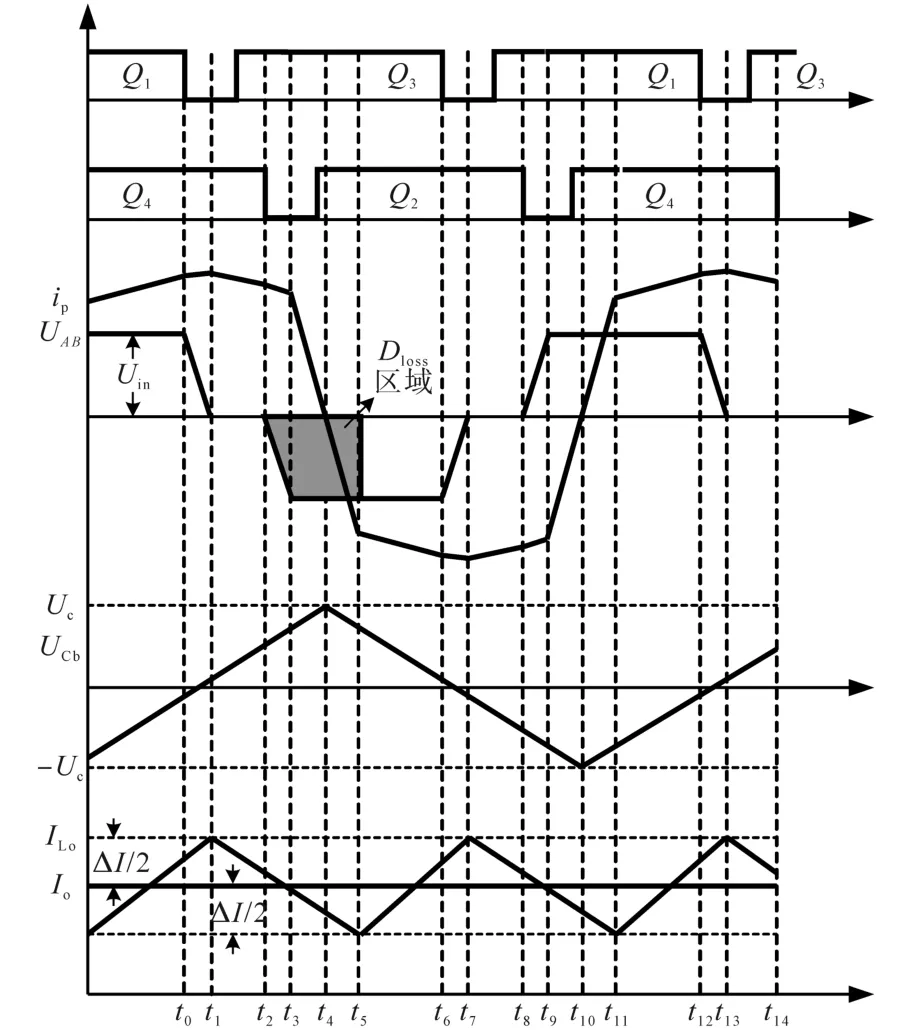
圖2 移相全橋ZVS變換器的主要波形圖Fig.2 Main waveforms of phase-shifted full-bridge ZVS converter

在1個開關周期內，變換器共有12種開關模態，由于其正負半周的對稱性，這里只分析正半周6種模態。圖3～圖9為這幾種模態下的等效電路，假設：1）所有器件為理想器件；2）C1=C3=Clead，C2=C4=Clag，其中Clead為IGBT超前臂并聯電容，Clag為IGBT滯后臂并聯電容。

模態0（0—t0）：如圖3，Q1，Q4導通，原邊電流ip流經變壓器T、整流二極管Da和Db為負載供電。

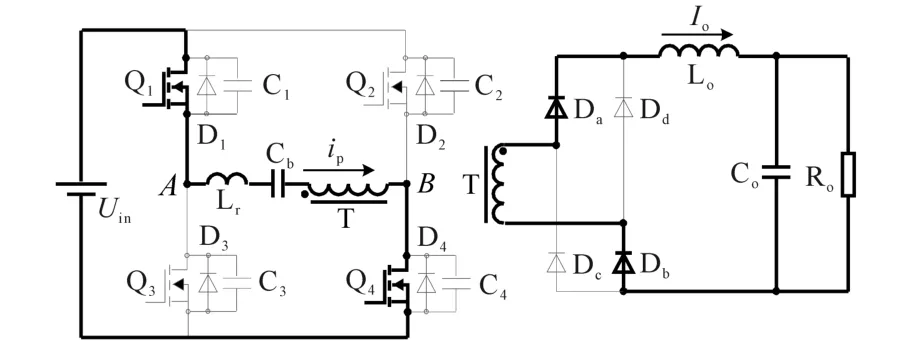
圖3 移相全橋ZVS 0—t0時刻等效電路圖Fig.3 Equivalent circuit of phase-shifted fullbridge ZVS converter in 0—t0

模態1（t0—t1）：如圖4，t0時刻，關斷Q1，此時C1充電而C3放電。電容C1電壓從0上升至Uin，而C3電壓從Uin下降至0。當C3電壓下降至0時，D3自然導通。該模態內近似認為ip不變。

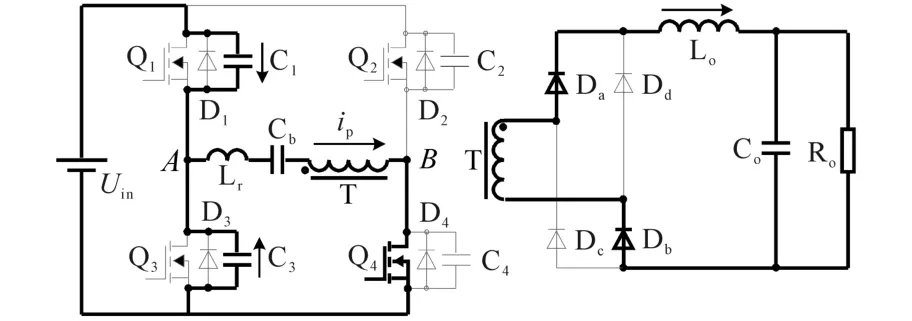
圖4 移相全橋ZVS t0—t1時刻等效電路圖Fig.4 Equivalent circuit of phase-shifted fullbridge ZVS converter in t0—t1

模態2（t1—t2）：如圖5，D3導通后，Q3的漏源極電壓被鉗位在0，此時開通Q3實現零電壓開通。但是由于ip方向未變，所以電流仍然流經D3。Q3實現零電壓開通的條件為：Q1，Q3的死區時間必須大于模態1持續的時間，則有：

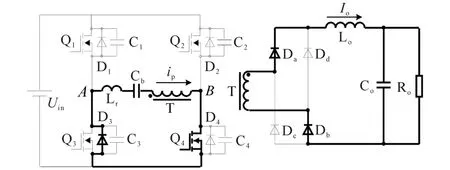
圖5 移相全橋ZVS t1—t2時刻等效電路圖Fig.5 Equivalent circuit of phase-shifted fullbridge ZVS converter in t1—t2

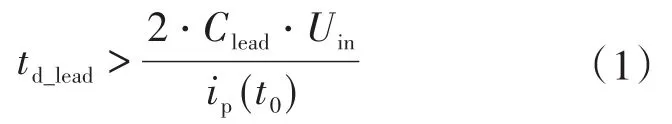
模態3（t2—t3）：如圖6，在t2時刻關斷Q4，此時C4電壓從0上升，C2電壓從Uin下降。原邊電流ip減小，不足以提供負載電流。此時，變壓器副邊4個整流二極管均導通進入續流階段。該模態內近似認為ip不變。

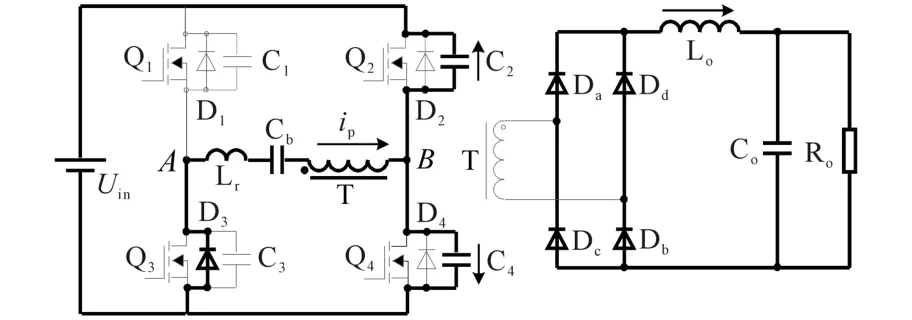
圖6 移相全橋ZVS t2—t3時刻等效電路圖Fig.6 Equivalent circuit of phase-shifted fullbridge ZVS converter in t2—t3

模態4（t3—t4）：如圖7，在t3時刻，由于D2的導通，Q2的漏源極電壓被鉗位在0，此時開通Q2，實現零電壓開通。但是由于ip方向未變，所以電流仍然流經D2。此時，變壓器原副邊并沒有耦合，Uin電壓全部加在Lr上，ip線性減小。當原邊電流下降至0，D2和D3自然關斷。

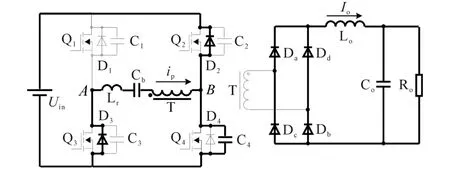
圖7 移相全橋ZVS t3—t4時刻等效電路圖Fig.7 Equivalent circuit of phase-shifted fullbridge ZVS converter in t3—t4

模態5（t4—t5）：如圖8，t4時刻，ip過0并流過Q2和Q3，由負方向線性增大。t5時刻，ip增大至-Io（t5）/n，其中Io為輸出濾波電感的平均電流，n為變壓器原副邊匝數比。此時變壓器原副邊耦合。Da和 Db截止，Dd和 Dc繼續導通。

圖8 移相全橋ZVS t4—t5時刻等效電路圖Fig.8 Equivalent circuit of phase-shifted fullbridge ZVS converter in t4—t5

模態 6（t5—t6）：如圖 9，在此階段，Q2，Q3導通，ip反向線性增大，與輸出電感電流Io呈匝數比關系。

圖9 移相全橋ZVS t5—t6時刻等效電路圖Fig.9 Equivalent circuit of phase-shifted fullbridge ZVS converter in t5—t6

2 移相全橋ZVS變換器的參數優化設計

本節將基于ZVS負載范圍對移相全橋變換器的關鍵參數進行優化設計，首先定義如下變量：系統容量P，輸入電壓Uin，輸出電壓Uo，開關頻率f，IGBT超前臂并聯電容Clead，IGBT滯后臂并聯電容Clag。

2.1 變壓器匝數比

移相全橋ZVS變換器輸入輸出電壓關系可以表示為

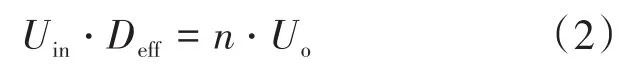
式中：Deff為系統有效占空比；n為變壓器原副邊匝數比。

在網壓最低的情況下，系統的占空比丟失最嚴重，考慮系統能夠接受的最大占空比丟失為Dloss，令此時Deff+Dloss=1，則變壓器匝數比可以根據下式求出：

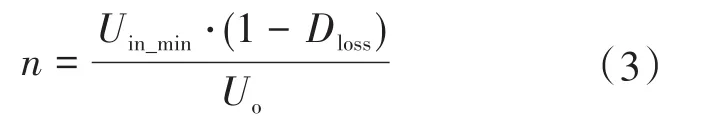
2.2 隔直電容

移相全橋ZVS變換器中隔直電容Cb的作用主要是防止變壓器偏磁飽和，因此隔直電容的引入必須盡量減小對電路的干擾，一般取其電壓峰值小于輸入電壓的5%。

由圖2可知，變壓器一個開關周期的正負半周原邊電流會對隔直電容進行充放電。以原邊電流的正半周為例，隔直電容電壓從-Uc減小至0，又反向增大至Uc，原邊電流的平均值可以根據變壓器副邊輸出電流通過匝數比等效計算。因此，根據隔直電容上電荷變化量等式，則有：

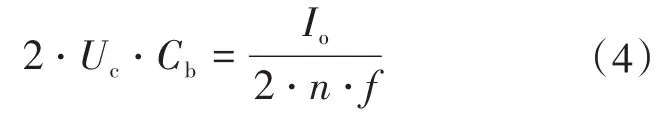
因此根據式（4），隔直電容可以求得：

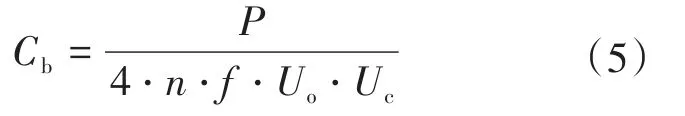
2.3 輸出濾波電感

輸出濾波電感Lo的主要作用為與輸出電容構成LC低通濾波器，可以濾除前端開關器件中的高頻諧波。

如圖2可知，在t1—t5時間段內，輸出電感電流從Io+ΔI/2下降至Io-ΔI/2，輸出電感電壓近似為Uo，該階段的持續時間可以表示為（1-Deff）/2f。根據輸出電感的伏秒平衡原理可得：

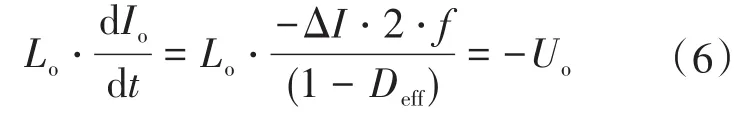
因此，輸出濾波電感可以根據式（6）計算求出：

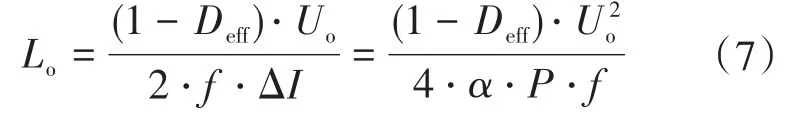
式中：Io為輸出濾波電感的平均電流；ΔI為紋波電流峰峰值；α為紋波系數，認為ΔI=2αIo。

2.4 諧振電感

移相全橋電路中諧振電感Lr的主要作用就是配合滯后臂的死區時間，實現滯后臂的ZVS。但是，諧振電感的設計十分復雜，較小的諧振電感將導致系統滯后臂軟開關范圍窄、工作效率低；過大的諧振電感又將使得系統占空比丟失嚴重，變換器的輸出電壓不能得到保證。

由前文分析可知，在1個開關周期內，移相全橋電路占空比丟失時間即為t2—t5時間段。在此階段內近似認為變壓器原邊電流ip呈線性變化，則有如下關系：

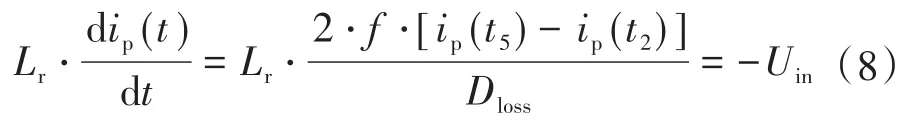
由于在t2，t5時刻，變壓器原副邊仍然存在耦合關系，因此這兩個時刻的電流值可以根據輸出電感的電流值折算至原邊求得。

在t5時刻，ip所對應的變壓器副邊電流即為輸出電感的波谷電流，其可以表示為

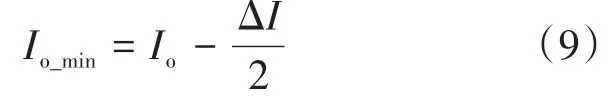
根據式（2）、式（7）和式（9）可以求得ip（t5）為

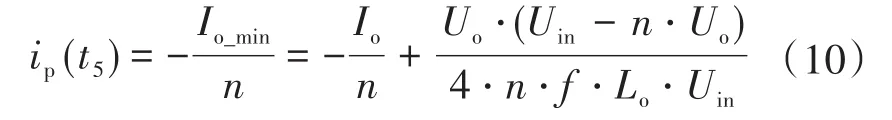
t2時刻輸出電感的電流值仍然可以根據電流下降階段的伏秒平衡原理求得，此時電流下降時間為占空比丟失時間，則有如下關系：

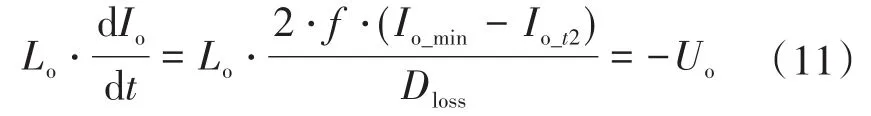
根據式（7）、式（9）和式（11）可求出ip（t2）為

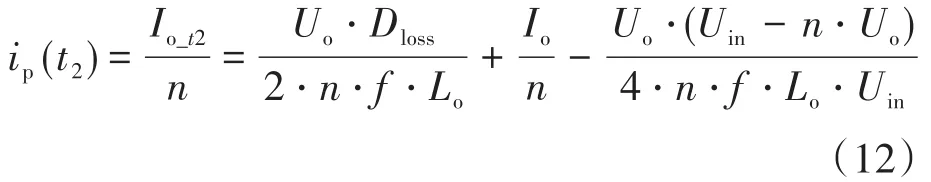
因此根據式（8）、式（10）和式（12），占空比丟失可以進一步求得：

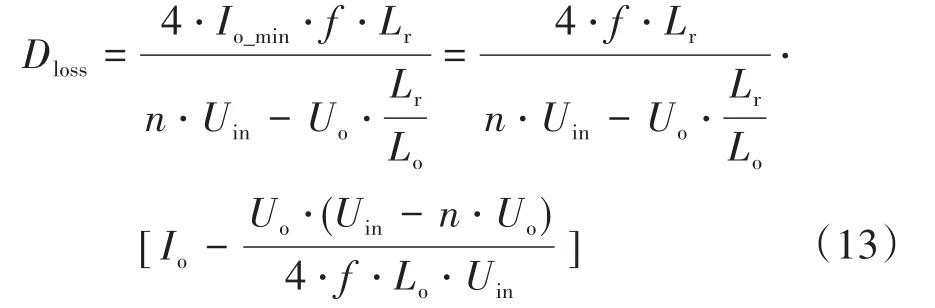
由式（13）可知，占空比丟失Dloss隨負載電流Io的增大而增大，隨輸入電壓的增大而減小。因此占空比丟失最嚴重的情況即為負載最大且輸入電壓最低工況下。在占空比丟失最惡劣情況下，系統若想仍然保證所需的輸出電壓就必須滿足如下關系：

根據式（13）可以求得諧振電感的表達式，如下所示：

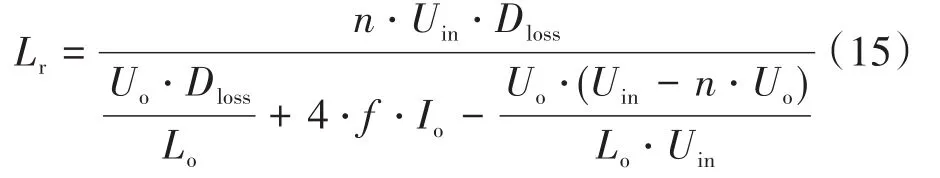
由前面的理論分析可知，滯后臂實現ZVS的條件為：t2時刻諧振電感存儲的能量必須大于等于滯后臂并聯電容完成換流過程所需要的能量，因此有如下關系式：

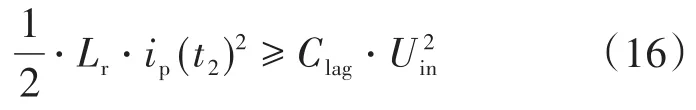
考慮能量相等的臨界情況，將式（12）代入式（16），可求出諧振電感的表達式為

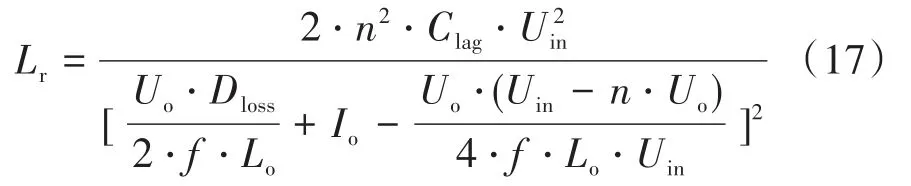
假設λ為負載系數，取值范圍為0～1（例如：半載情況λ=0.5），Io代表滿載時的負載電流，則在某一負載情況下，將式（15）和式（17）寫成兩個函數的形式，則有：

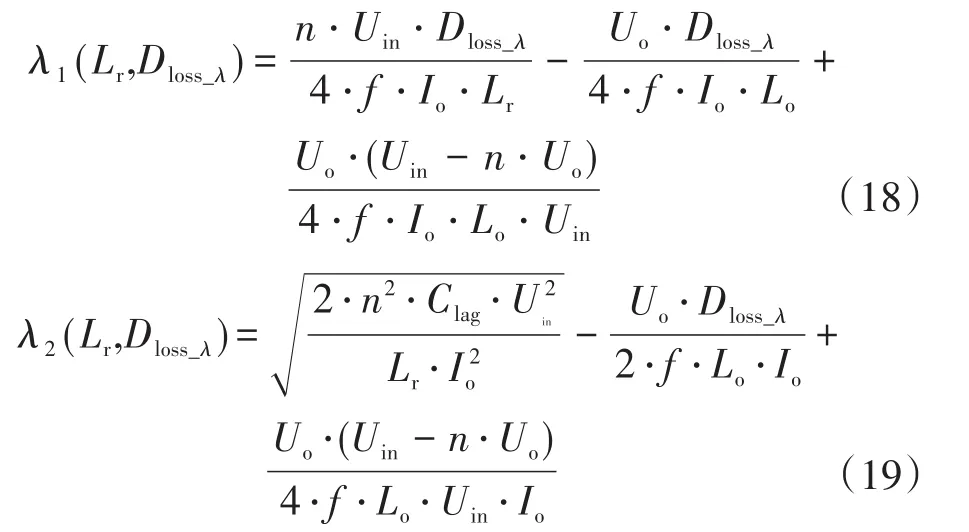
式中：λ1，λ2為因變量；Dloss_λ，Lr為自變量；Dloss_λ為λIo情況下的占空比丟失。

根據式（18）和式（19），畫出λ1，λ2兩個函數的曲面圖，這兩個曲面的交集即為該系統滿足臨界軟開關條件所有點的集合，記為M（λ，Dloss_λ，Lr）。該集合表示的意義為：在已知參數條件下，當諧振電感選為Lr時，滯后臂實現ZVS的范圍為（λ～1）Io，在λIo負載條件下的占空比丟失為Dloss_λ。

根據系統的散熱能力，確定本系統實現ZVS軟開關負載范圍λ，在集合M（λ，Dloss_λ，Lr）中將該點提取出來。值得注意的是：在選取M（λ，Dloss_λ，Lr）集合中某一個點之后，需要驗證在該諧振電感Lr的情況下，總占空比是否小于1，即式（14）是否成立。若不成立，需要適當減小諧振電感值進行重新選擇，直至滿足式（14）條件為止。

2.5 IGBT死區時間

為了使超前臂實現ZVS，需要使超前臂的死區時間滿足式（1），to時刻的原邊電流可以通過輸出濾波電感波峰值折算值原邊計算，因此超前臂死區時間可以根據下式選取：

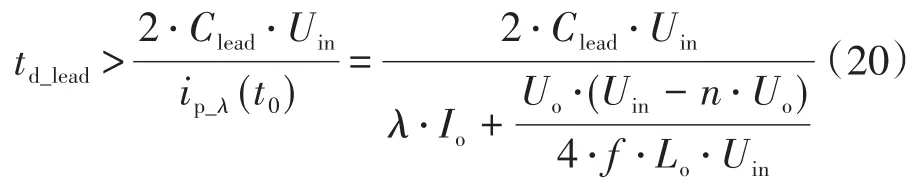
式中：ip_λ（t0）為λIo負載情況下t0時刻的原邊電流。

滯后臂死區時間必須大于Q4斷開后其并聯電容Clag完成換流過程所需要的時間，則有：

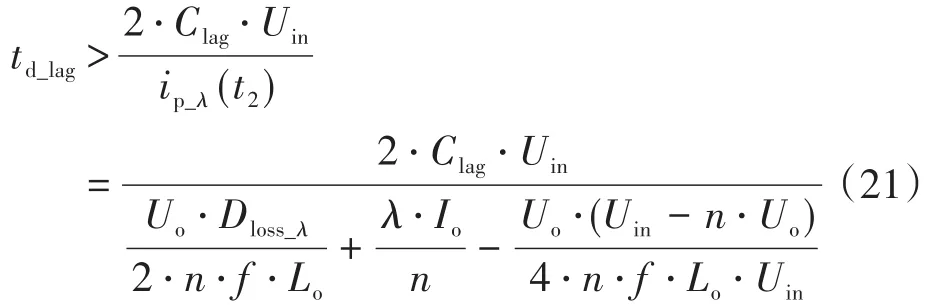
式中：ip_λ（t2）為λIo負載情況下t2時刻的原邊電流。

同時，Q2應該在原邊電流ip下降至0前開通，即Q2和Q4的死區時間應該小于原邊電流ip下降至0所需的時間。原邊電流ip下降至0所需的時間可以表示為

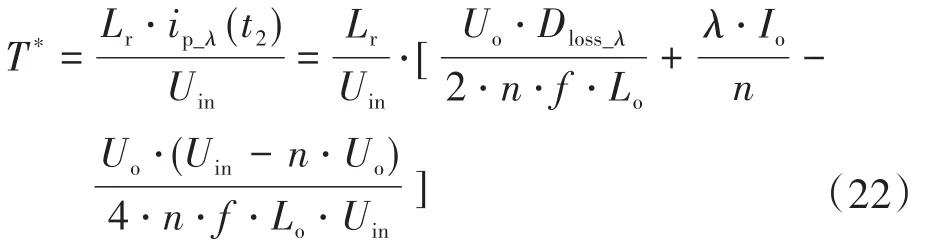
因此，根據式（21）和式（22）可知，滯后臂死區時間應該滿足如下條件：

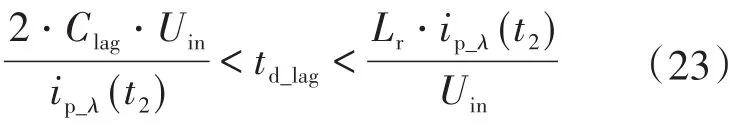
2.6 參數設計流程

綜上分析，繪制移相全橋ZVS變換器關鍵參數優化設計流程框圖，如圖10所示。

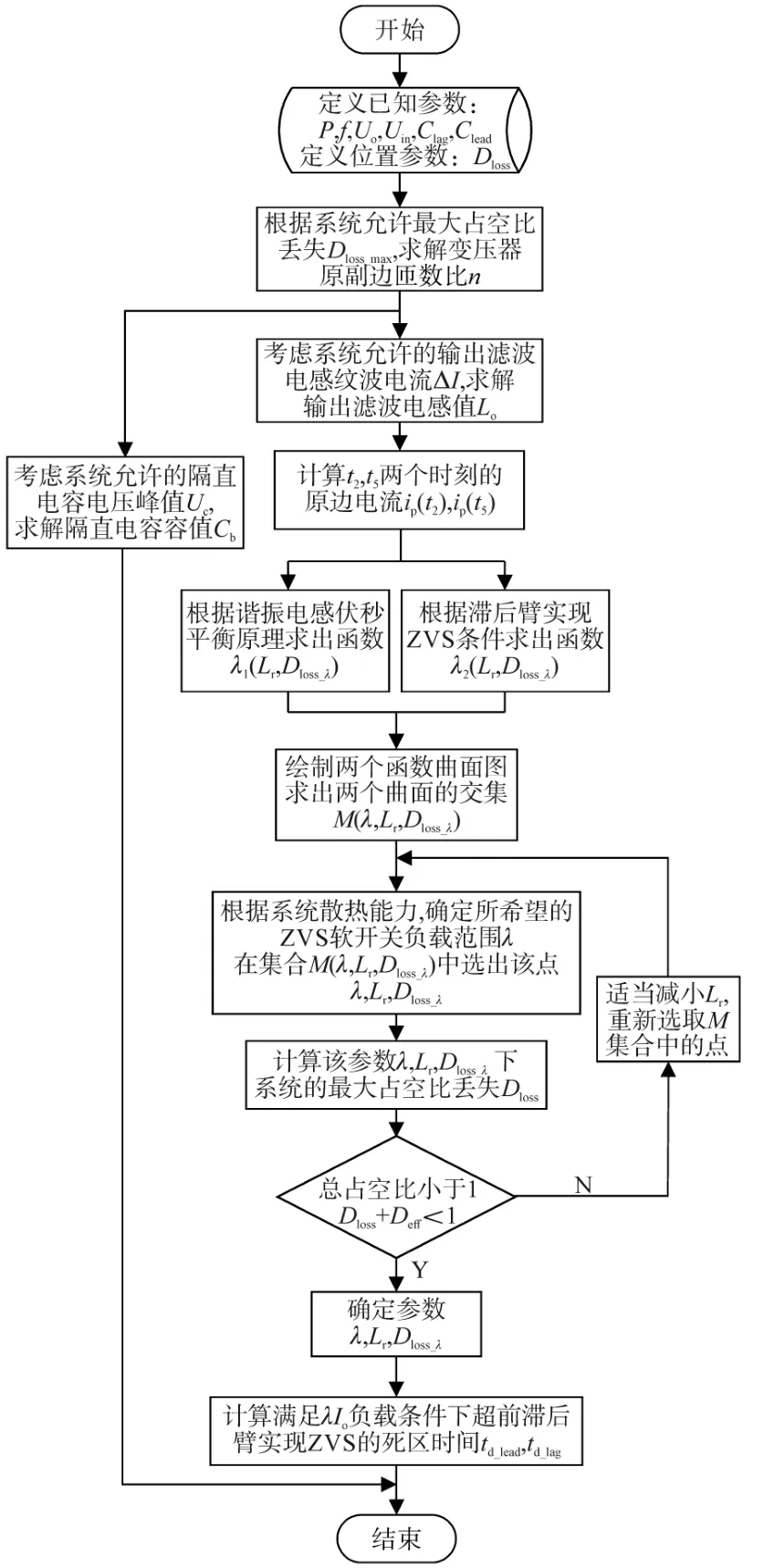
圖10 移相全橋ZVS變換器關鍵參數優化設計流程框圖Fig.10 Optimized design flow diagram of main parameter based on phase-shifted full-bridge ZVS converter

3 實驗結果與分析

根據前文的理論分析，本小節將通過搭建45 kW的實驗樣機，驗證其正確性。

表1為系統的電氣參數。

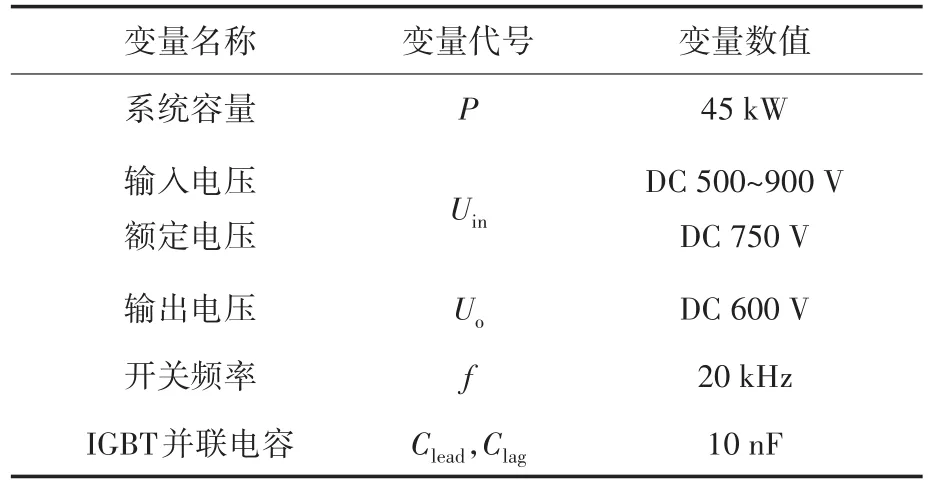
表1 系統電氣參數Tab.1 System electrical parameters

下面根據圖10所示流程框圖進行本系統的關鍵參數設計。

3.1 變壓器匝數比

考慮在網壓最低DC 500 V時，系統能夠允許的最大占空比丟失為15%，則根據式（3）可以求得變壓器原副邊匝數比為0.7。為了降低副邊整流二極管的電壓應力，這里采用變壓器副邊雙繞組型式，匝數比取4：3：3，等效匝數比為n=2/3。

3.2 隔直電容

考慮隔直電容的峰值電壓Uc為輸入電壓的3%，則根據式（5）可以計算出隔直電容容值為84 μF，這里取Cb=80 μF。重新計算隔直電容電壓峰值Uc=16.7 V。

3.3 輸出濾波電感

考慮額定輸入電壓、10%滿載條件下，輸出濾波電感電流呈臨界連續模式狀態，即電感電流紋波系數α=0.1，則根據式（2）和式（7）可以計算出輸出濾波電感值為485 μH，這里取Lo=400 μH。重新計算輸出濾波電感電流紋波為ΔI=17.3 A。

3.4 諧振電感

系統的額定輸出電流Io可以根據輸出功率和輸出電壓求得：Io=P/Uo=71.4 A。將表1中的已知參數以及前文計算的n，Lo，ΔI代入式（18）和式（19），同時令Lr單位為μH，可以求得：

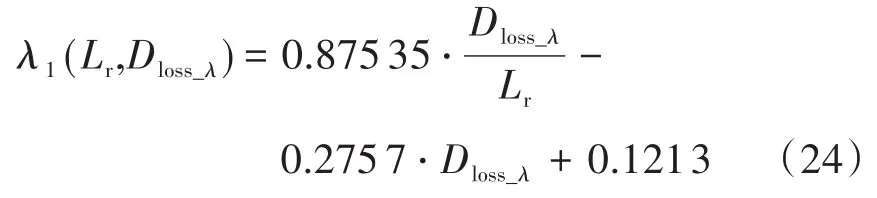
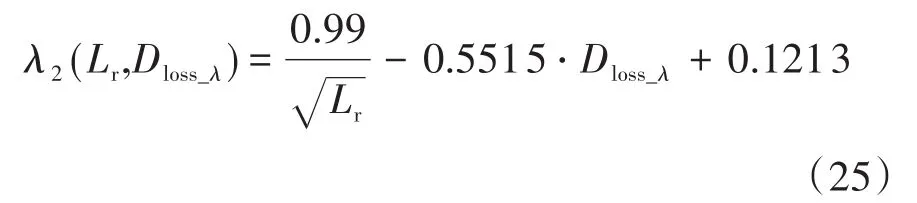
根據式（24）和式（25）繪制出兩個函數的曲面圖如圖11所示。圖11中深黑色空間曲線即為兩個曲面的交線。根據本系統的散熱能力，這里考慮ZVS軟開關負載范圍為40%，即λ=0.4。在空間曲線上選出相應的參數點M（0.42，10，0.03），該點的意義為：在已知參數下，諧振電感Lr選取10 μH時，系統可以實現0.42倍滿載以上的ZVS，此時的占空比丟失為0.03。

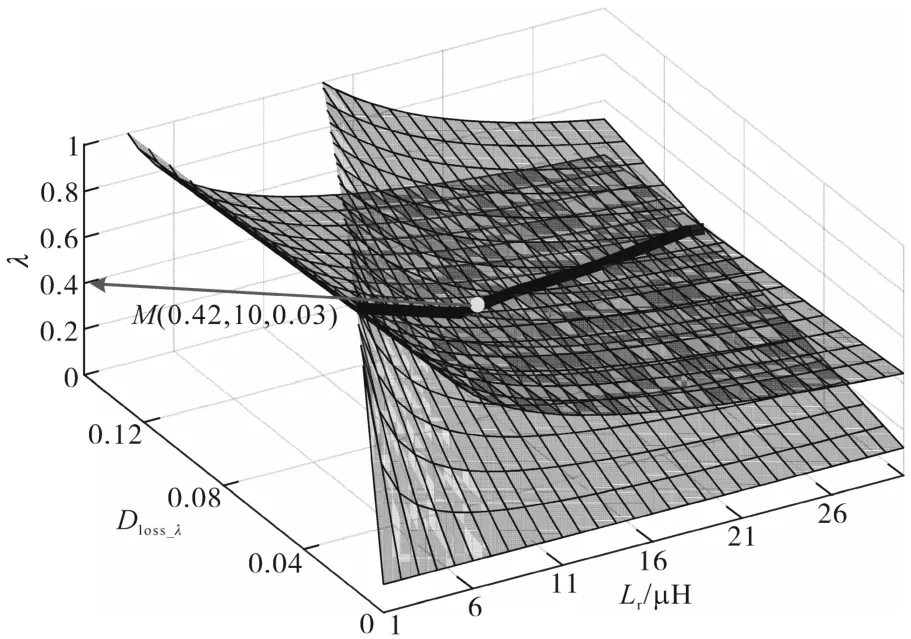
圖11 λ1和λ2函數的曲面圖Fig.11 Surface plot of λ1and λ2function

最后通過計算在此諧振電感條件下系統的總占空比是否小于1，來驗證參數選取的合理性。根據式（2）、式（13）以及式（14）可以求得有效占空比Deff、占空比丟失Dloss分別為 0.79，0.14，總占空比為0.93，滿足小于1的條件，因此諧振電感參數設計合理。在此參數條件下，系統滯后臂實現ZVS的臨界負載為45 kW×0.42=19 kW。

3.5 IGBT死區時間

為了使超前臂實現ZVS，需要使超前臂的死區時間滿足式（20），可以通過求出不等式右側的最大值來確定超前臂死區時間的范圍。根據式（18）和式（19），當Lr=10 μH時，可以求出：DC 500 V輸入電壓條件下的λ=0.26；DC 750 V輸入電壓條件下的λ=0.42；DC 900 V輸入電壓條件下的λ=0.5。因此，不等式右側的最大值可以計算為0.47 μs，這里取超前臂死區時間td_lead=1 μs。

滯后臂死區時間可以根據式（21）～式（23）進行選取計算。將已知參數代入式（21）求得其最小值為0.42 μs；同理，根據式（22）可以計算其最大值為0.56 μs。這里取滯后臂死區時間td_lag=0.5 μs。

綜上分析，該系統的關鍵參數如表2所示。

表2 系統關鍵電氣參數Tab.2 Key electrical parameters of system

下面搭建45 kW移相全橋電路實驗平臺，實驗參數如表1和表2所示，實驗結果如下：

1）在網壓DC 750 V、輸出功率40 kW工況下，觀察系統隔直電容電壓Uc和輸出濾波電感電流ILo的情況，如圖12所示。

圖12 網壓DC 750 V、輸出功率為40 kW工況下，隔直電容電壓Uc和輸出濾波電感電流ILo的實驗波形圖Fig.12 Test waveforms of Uc，ILounder the conditions of Uin=750 V and P=40 kW

由圖12可知，隔直電容電壓峰值Uc為16 V，輸出濾波電感紋波電流ΔI=17.6 A。

2）在網壓DC 750 V，輸出功率40 kW、19 kW以及10 kW三種工況下，觀察移相全橋滯后臂實現ZVS的情況，如圖13所示。

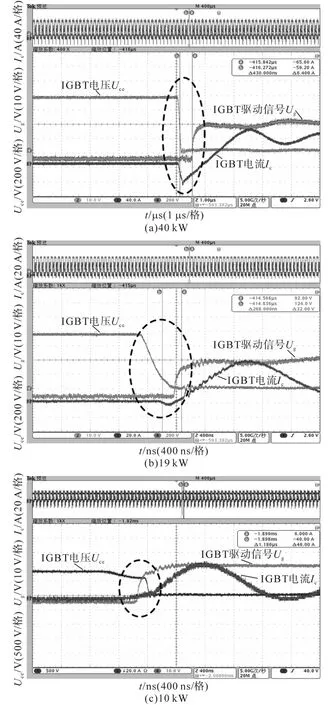
圖13 不同負載下滯后臂驅動信號及電壓電流實驗波形圖Fig.13 Test waveform of lag arm gate signal，voltage and current in different load

由圖13可知：在負載40 kW時，滯后臂的并聯電容電壓下降至0后，經過一小段時間滯后臂開通，很好地實現了ZVS軟開關；同理，在負載19 kW時，滯后臂的并聯電容電壓下降至0的時刻與滯后臂開通時刻基本重合，可以近似判斷該工況下系統滯后臂處于臨界ZVS軟開關狀態；在負載為10kW時，滯后臂在其并聯電容電壓下降至0之前就已經導通，因此該工況下滯后臂沒有實現ZVS軟開關。

3）在網壓最低DC 500 V、輸出功率40 kW時，觀察移相全橋輸出電壓及占空比丟失情況，如圖14和圖15所示。

圖14 輸入電壓為500 V、輸出功率為40 kW工況下的輸入、輸出電壓實驗波形圖Fig.14 Test waveforms of input and output voltage under the conditions of Uin=500 V and P=40 kW

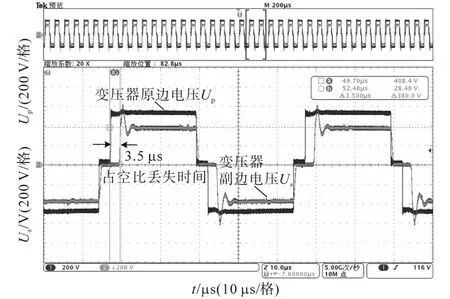
圖15 輸入電壓為500 V、輸出功率為40 kW工況下的變壓器原副邊電壓實驗波形圖Fig.15 Test waveforms of primary and secondary voltage of transformer under the conditions of Uin=500 V and P=40 kW

由圖14和圖15可知，在輸入電壓為DC 500 V、輸出功率為40 kW工況下，輸出電壓可以達到DC 600 V；同時占空比丟失時間為3.5 μs，占空比丟失為0.14。

綜上分析，實驗結果與理論分析基本保持一致，驗證了理論分析的正確性。

4 結論

本文針對移相全橋ZVS電路復雜的參數設計問題，提出了一種基于ZVS負載范圍的移相全橋變換器的參數優化設計方法。實驗結果表明，該方法可以根據系統所希望實現的軟開關負載范圍，確定諧振電感、IGBT死區等關鍵參數的最優解，這將為實際工程應用中移相全橋的參數設計提供十分重要的指導與幫助。