垂直非均布移動輪載作用下瀝青路面結構數值分析*

蔣 鑫 陳 戈 王 鑫 武琨璐 邱延峻

(1.西南交通大學土木工程學院 成都 610031； 2.西南交通大學道路工程四川省重點實驗室 成都 610031；3.西南交通大學高速鐵路線路工程教育部重點實驗室 成都 610031)

目前瀝青路面結構分析多采用垂直均布靜載，無法反映實際輪胎-路面接觸應力強烈的非均布特征。針對實際非均布輪載作用的復雜性，胡小弟等[1]運用自主研發的輪地壓力靜態測試裝置對多種輪胎的接地壓力分布與路面力學響應進行了測驗，并歸納了不同車型輪胎的面積折減率、橫向壓力分布等規律；A.Said等[2]根據輪胎壓力實測數據提出了高壓輪胎、低壓輪胎接地應力的非均布簡化方程；Jiang等[3]運用三維有限元法分析了不同類型垂向非均布靜載對瀝青路面力學響應的影響，比較了均布荷載與垂向非均布荷載下瀝青路面結構力學響應的差異；De Beer等[4]運用半解析有限元法對比了實測非均布垂直荷載與均布荷載對薄瀝青路面力學響應的影響；黃志義等[5]運用連續有限層法對實測非均布荷載與均布荷載進行了黏彈性對比分析。

這些研究著力于輪胎接地壓力分布形狀、靜態力學響應計算及均布與非均布荷載的對比，但對相同輪載大小、不同接地應力分布作用下的力學響應規律缺少專門研究。基于上述背景，本文試圖探討垂直非均布移動輪載作用下瀝青路面結構力學響應的變化規律，從而為道路行車試驗時科學加載及路面結構精細化分析提供參考。

1 3D-Move Analysis軟件數值建模關鍵技術

3D-Move Analysis系美國The University of Nevada, Reno(UNR)開發的一款基于三維連續有限層法的瀝青路面結構電算軟件。前期研究表明，其在瀝青面層黏彈性及復雜荷載考慮等方面均具有獨到之處，下面結合本文欲分析的問題，就建模中的關鍵技術做扼要介紹。

1.1 荷載復雜性的考慮

3D-Move Analysis 程序實施的具體步驟如下：①將復雜的荷載離散化成單元荷載；②利用傅里葉展開公式將單元荷載轉化為諧波分量；③通過疊加原理得到X和Y方向的總荷載傅里葉級數。表面荷載在平面上被分為N×M份，荷載在離散時會留下足夠大的無荷載作用區域以免對下個周期的加載產生影響。離散化方式見圖1，具體轉化過程如式(1)～(4)。

(1)

(2)

(3)

(4)

式中：q(x,y,t)為經過轉換t時刻的總響應；q(j,k)為坐標(j,k)處單元荷載；m、n為單元荷載所在坐標；Δx、Δy為單元長度；c為行車速度；t為時間。

圖1 3D-Move analysis程序表面荷載離散方式

該軟件因所采用的三維連續有限層法的優勢，即通過將表面荷載轉化為含時間、速度變量的傅里葉級數，可以很好地考慮表面荷載的移動性、非均布等特點。具體實施時，3D-Move Analysis程序中Δx、Δy單元長度根據自帶實測荷載庫或用戶自行輸入確定。

1.2 瀝青面層黏彈性的考慮

由于瀝青具有黏彈性，其彈性模量依賴于溫度和荷載作用時間，直接影響著路面使用性能，國內外學者針對這一特性進行了大量研究，如孔思林等[6]利用三維有限元法對車輛在制動與啟動時的力學響應進行了黏彈性分析，確定了瀝青材料動態模量模型。

3D-Move Analysis通過在不同模型下構建動態模量主曲線來實現瀝青路面的黏彈性分析，程序包含4種主曲線生成模型，即根據試驗數據確定動態模量的對稱Sigmoidal模型、非對稱Sigmoidal模型和Hust-sayegh模型及通過瀝青面層混合料本身的特性來預測動態模量的Witczak模型。前3種模型確定瀝青面層動態模量主曲線過程如下：①將不同溫度、頻率下的實測動態模量數據輸入模型；②利用時間-溫度疊加原理繪制參考溫度的主曲線；③利用位移因子，得到分析溫度的動態模量主曲線。第4種模型則為預測模型，可通過瀝青混合料的級配、體積特性、黏結劑屬性等預測指定溫度下的瀝青模量主曲線。

2 數值分析模型建立

2.1 路面結構組合與材料參數

文獻[7]中Example B的路面結構，以瀝青面層+級配碎石基層+土基組成的三層式瀝青路面結構為例，結構層厚度、材料參數等見圖2，其中：E、ζ、υ分別為彈性模量、阻尼比及泊松比。

圖2 路面結構參數

動態模量計算選擇對稱Sigmoidal模型，即通過試驗測得不同溫度、頻率下的瀝青模量，再用對稱Sigmoidal模型將其擬合成動態模量主曲線。主曲線計算方法見式(5)。

(5)

式中：E*為瀝青材料的動態模量，psi；α、δ為擬合參數，δ為動態模量的最小值，δ+α為動態模量的最大值，psi；β、γ為Sigmoidal函數的形狀參數；tr為參考溫度下的荷載作用時間；η為黏度，mPa·s；ηr為參考溫度下的黏度，mPa·s。

試驗數據下由該模型在溫度為25 ℃時生成的瀝青動態模量主曲線見圖3。

圖3 瀝青面層動態模量主曲線

2.2 垂直非均布移動輪載

選用3D-Move Analysis程序中自帶的Kistler MODULAS數據庫中所列荷載。該數據庫引用自M.Sime等[8]利用壓力傳感器測得的多組輪胎接地應力，其中不同車速下的垂向應力分布多達192組，胎壓范圍為420～1 000 kPa，輪載范圍為4.5～62 kN。在Kistler MODULAS數據庫中車速V=32 km/h時，GOOD YEAR295/75 R22.5型輪重為25 kN輪胎的接地壓強分布見圖4，如參照國內現行公路瀝青路面設計規范[9]中的BZZ-100雙輪單軸標準軸載，可認為前二者胎壓偏低，0.69 MPa與0.7 MPa相當接近，而0.827 MPa則可認為胎壓偏高。圖4a)、b)表明，當胎壓偏低時，輪胎接地壓強沿胎寬方向呈凹型分布；圖4c)屬于由低壓輪胎到高壓輪胎過渡狀態，輪胎接地壓強沿胎寬方向呈凹凸交錯分布；圖4d)為胎壓偏高時，輪胎接地壓強沿胎寬方向呈凸型分布。p=0.517 MPa(低壓輪胎)與p=0.827 MPa(高壓輪胎)不同車速下的輪胎路面接地應力情況分布見圖5、圖6。

圖4 4種非均布輪載的分布(V=32 km/h)

圖5 胎壓p=0.517 MPa時接地壓強分布

圖6 胎壓p=0.827 MPa時接地壓強分布

3 主要計算結果分析與討論

3.1 胎壓致接地壓強非均勻分布的影響

當車速V=32 km/h時，圖2所示路面結構土基頂豎向壓應變、瀝青面層層底行車方向拉應變等力學響應的橫向分布分別見圖7、圖8，同時給出按照文獻[9]所述設計軸載，即胎壓、接地壓強均為0.7 MPa的雙圓垂直均布荷載的計算結果以作對比。

圖7 土基頂壓應變橫向分布

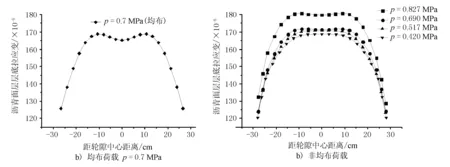
圖8 瀝青面層層底拉應變橫向分布

由圖7、圖8可見，與均布荷載類似，4種不同非均布荷載作用下土基頂豎向壓應變沿胎寬均呈單峰狀分布，最大壓應變的位置始終位于雙輪中心處。而瀝青面層底拉應變盡管仍呈雙峰馬鞍狀，但行車方向最大拉應變的位置隨輪胎接地壓強的減小向雙輪輪隙中心處轉移。在相同輪重非均勻分布情況下，瀝青面層層底拉應變與土基頂壓應變均隨著輪胎接地壓強的減小而減小，但二者影響程度有所不同，當非均布荷載胎壓從0.827 MPa減小到0.420 MPa時，土基頂最大壓應變減少1.72%，而瀝青面層層底最大拉應變減少6.67%，輪胎接地壓強對瀝青面層底拉應變的影響強于土基頂壓應變。

進一步討論輪載非均布情況下輪胎接地壓強的高低對瀝青面層底最大拉應變發生位置的影響，具體見圖9。

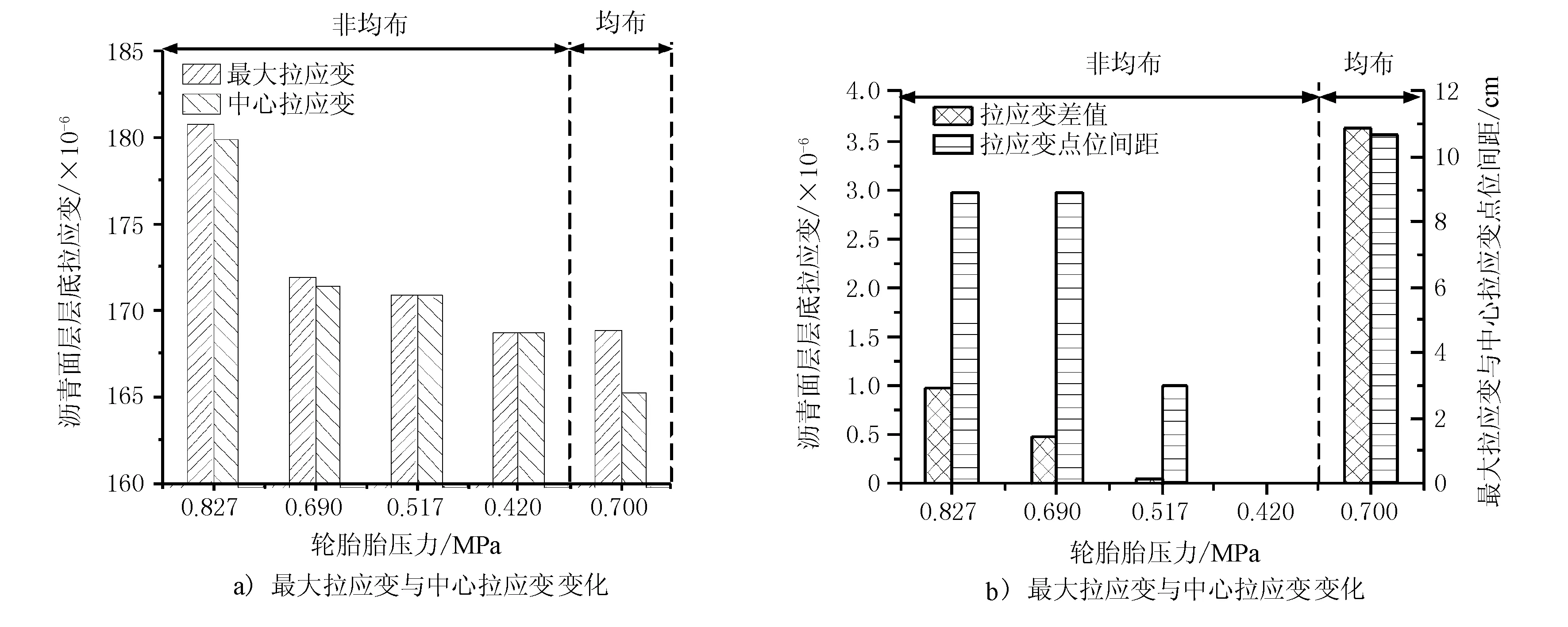
圖9 最大拉應變變化

由圖9可見，當胎壓偏高(p=0.827 MPa)或處于高、低胎壓過渡時(p=0.690 MPa)，二者瀝青面層底行車方向最大拉應變發生于輪胎內與雙輪內邊緣相距1/8胎寬處，與均布荷載(p=0.70 MPa)最大拉應變位置相似，這可能是均布荷載采用圓形分布，中部集中，與高壓輪胎作用下接地應力凸型分布相似；當胎壓偏低時(p=0.517，0.420 MPa)，隨著胎壓減小，輪地接觸壓強形態發生變化，瀝青面層底行車方向最大拉應變位置逐漸向中心移動，胎壓低到一定程度后(如p=0.420 MPa)瀝青面層層底最大拉應變位置調整為雙輪輪隙中心，這說明胎壓偏低時瀝青面層底最大拉應變的最不利點位變化相對較大。

3.2 車速的影響

在路面溫度為25 ℃情況下，p=0.517 MPa(胎壓偏低)、p=0.827 MPa(胎壓偏高)2種胎壓情況與均布荷載車速變化時，土基頂壓應變與瀝青面層底面行車方向拉應變分布分別見圖10、圖11。

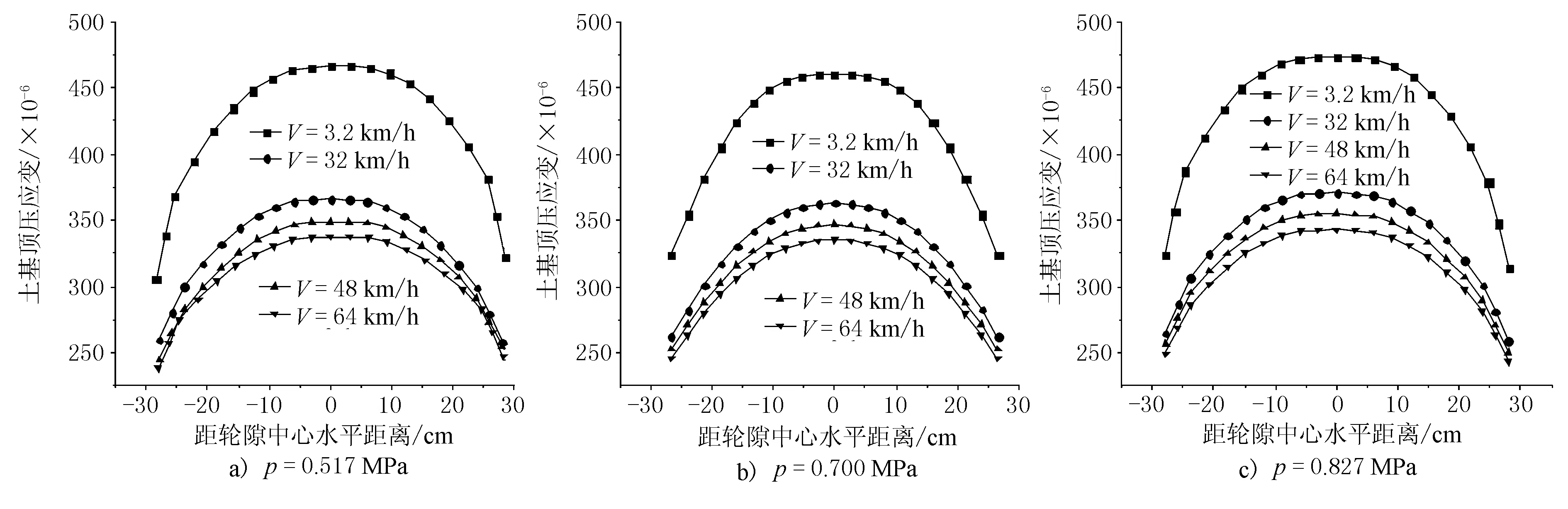
圖10 土基頂壓應變橫向分布隨車速變化

圖11 瀝青面層層底拉應變橫向分布隨車速變化

由圖10、圖11從總體來看，對于土基頂壓應變，其最不利點位的位置一直位于雙輪中心不發生改變。而隨著車速的增加，與均布荷載類似，非均布荷載情況下瀝青面層層底行車方向拉應變與土基頂壓應變均呈下降趨勢，且減小的幅度逐漸變小。這是由于瀝青面層的動態模量隨著頻率的增大而增大，但達到一定值后，其增大的幅度會隨著頻率的增大而趨于平緩。

不同胎壓情況下隨速度變化最大拉應變與中心拉應變的數值變化與距離變化關系見圖12～圖14。由圖12～圖14可見，當胎壓偏高時(p=0.827 MPa)，隨著車速增加，瀝青面層底最大拉應變位置基本不變，均處于輪胎內與內側邊緣靠近處。當車速為3.2 km/h時，最大拉應變與雙輪中心處拉應變相差7.71×10-6，降幅為2.82%，而當車速為64 km/h時，最大拉應變與雙輪中心處拉應變相差0.64×10-6，降幅為0.39%，這說明隨著車速的增加，當胎壓偏高時瀝青面層底最大拉應變與雙輪中心處拉應變更為接近，均布荷載情況下瀝青面層底拉應變的變化規律與胎壓偏高時類似。

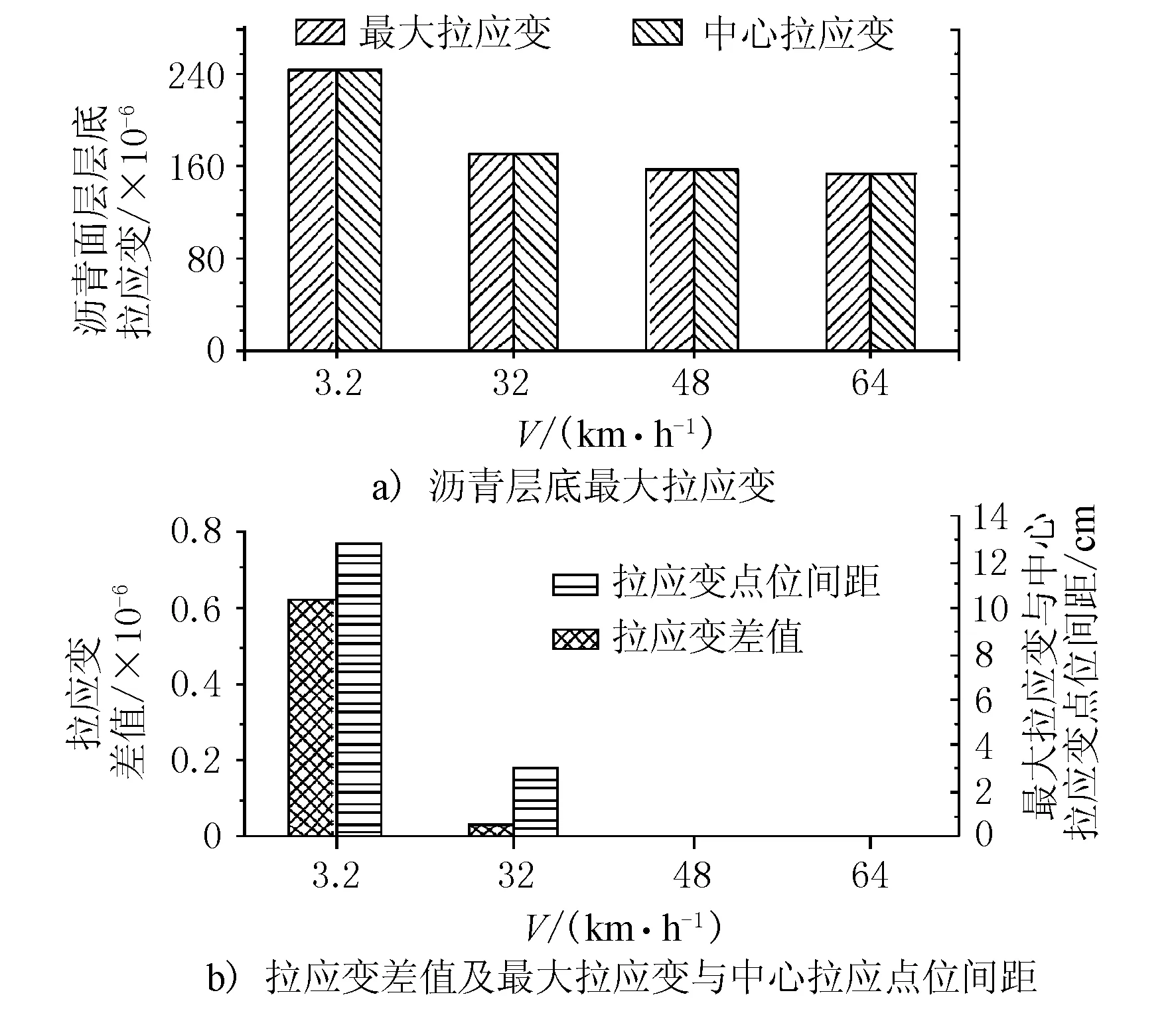
圖12 p=0.517 MPa最大拉應變

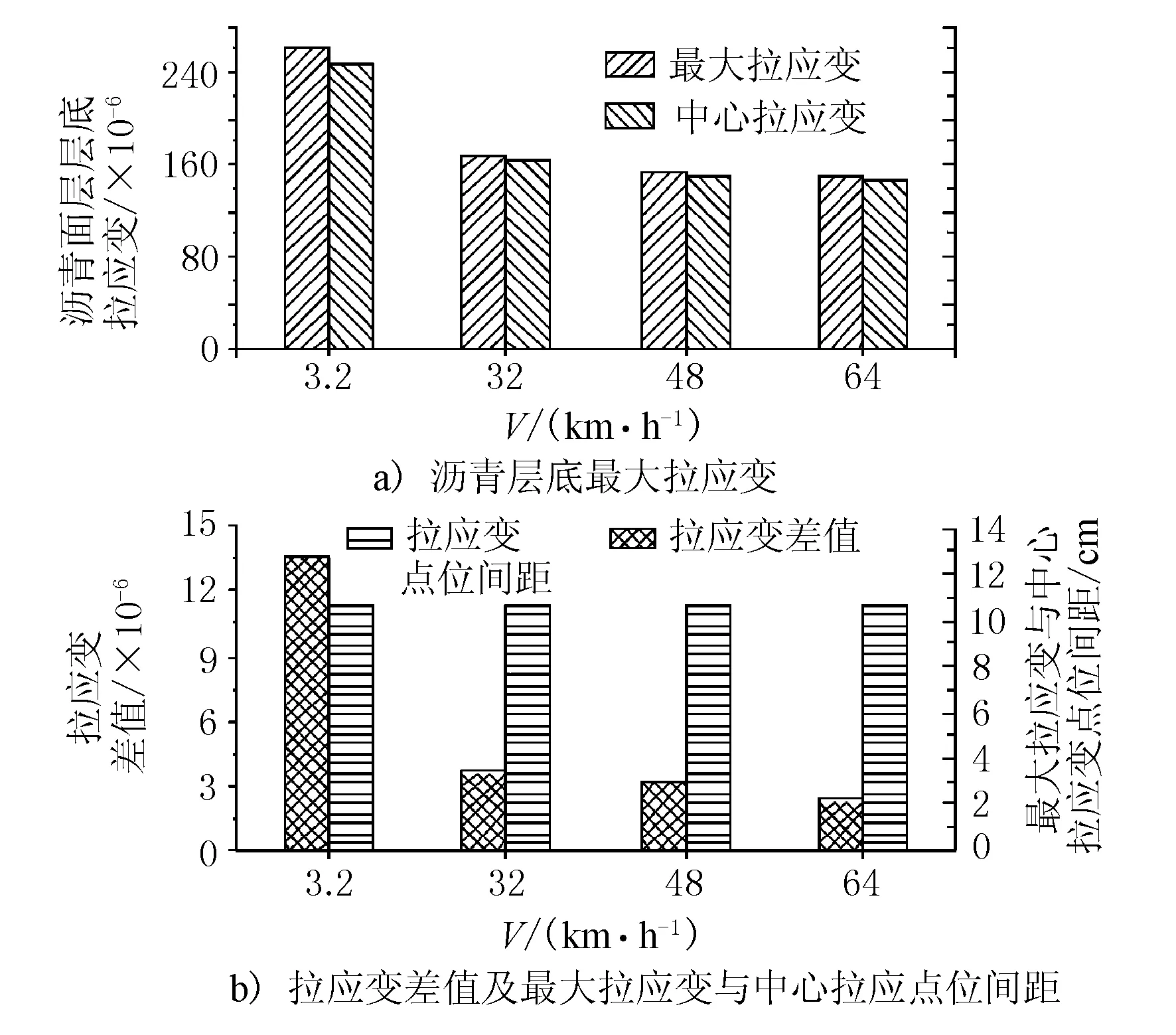
圖13 p=0.700 MPa最大拉應變

圖14 p=0.827 MPa最大拉應變

當胎壓偏低時(p=0.517 MPa)，如車輛低速行駛(V=3.2 km/h)，其最大拉應變位置位于輪胎內與內側邊緣相距1/4胎寬處，而隨著車速的增加，行車方向最大拉應變位置向中間靠攏，最后調整為輪胎中心處(車速V=48 km/h)。這說明胎壓偏低時，車速變化對瀝青路面面層層底行車方向拉應變影響更大，但胎壓偏高時，車速變化對瀝青面層底最大拉應變位置影響并不大。

鑒于路面結構開展現場動測試驗時，傳感器提前預埋于路面結構內部，并盡量設法控制以輪胎固定位置(一般為一側輪胎中心處或雙輪輪隙中心處)駛過路面內部預埋傳感器的正上方，如Middleton等人在開展現場動測實驗時將電阻應變片埋設于雙輪中心下方0.5 m處以測得水平應變[10-11]。然而上述計算表明輪載的垂向非均勻分布會導致輪胎中心處或雙輪輪隙中心處瀝青路面結構內動力學響應并非始終保持最大，不能獲得真正意義上的最不利力學響應，從而導致路面結構性能預測嚴重失真。

4 結語

1) 垂直荷載的非均勻分布形式對瀝青面層的影響遠大于土基。當胎壓偏高時致胎寬方向接地壓強呈凸型非均勻分布時，瀝青面層底最大拉應變位置與均布荷載作用下最大拉應變位置相近；當胎壓偏低致接地壓強呈沿胎寬方向凹形非均勻分布時，會較大程度地影響最大拉應變位置，且胎壓越低，最大拉應變越向兩輪中心處靠近。

2) 隨著車速增加，與均布荷載類似，胎壓偏高或偏低致接地壓強非均布時瀝青面層底拉應變的橫向變化均趨于緩和，在一定速度范圍內，胎壓偏高致接地壓強呈沿胎寬方向凸形分布時瀝青面層底的最大拉應變位置變化不大，但胎壓偏低導致接地壓強呈沿胎寬方向凹形分布時，瀝青面層底最大拉應變將向兩輪中心處靠近。

3) 如現場試驗條件允許，開展瀝青路面結構現場動測時，可根據垂直非均布移動荷載的性態合理確定加載位置，以更準確地捕捉不同情況下力學響應，尤其是瀝青面層底拉應變的最不利值。