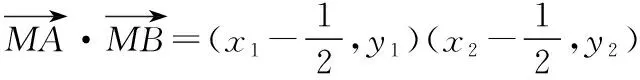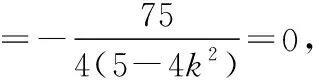創新性優秀原創試題選登

山東 叢以權 廣東 龍 宇 黑龍江 李偉勝

1.【研發題】

為紀念中國共產黨成立100周年，加深青少年對黨的歷史、黨的知識、黨的理論和路線方針的認識，激發愛黨愛國熱情，堅定走新時代中國特色社會主義道路的信心，某校舉辦了黨史知識競賽.競賽規則是：兩人一組，每一輪競賽中，小組兩人分別各答3道題，若答對題目總數不少于5道題，則獲得一個積分.已知甲、乙兩名同學一組，甲同學和乙同學每道題答對的概率分別是p1和p2，且每道題答對與否互不影響.

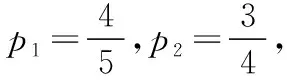
【考查目標】

本題主要考查二項分布與導數的綜合，要求學生能從生活實踐或學習探索層面的問題情境中提煉出數學問題，并解決問題，考查數據處理能力、運算求解能力，落實數學運算的核心素養.

【名師指導】

(1)利用所給數據和互斥事件的概率求值;(2)根據(1)形成p1p2=t的函數p(t),對函數求導，求出函數的最大值，再由np≥5即可求出所求.

【解題思路】

(1)設同學甲和同學乙答對的題目個數分別為a1和a2，所以所求的概率

P=P(a1=2,a2=3)+P(a1=3,a2=2)+P(a1=3,a2=3)

(2)他們在一輪競賽中獲得一個積分的概率

P=P(a1=2,a2=3)+P(a1=3,a2=2)+P(a1=3,a2=3)

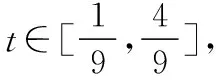
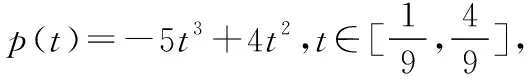
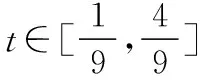
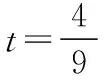
甲、乙兩同學在n輪競賽中獲得的積分數X滿足X～B(n,p)，

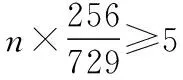
所以若甲、乙同學想至少獲得5個積分，理論上至少要進行15輪競賽.

2.【研發題】

(1)若n=2，求分數X的分布列;

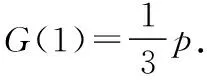
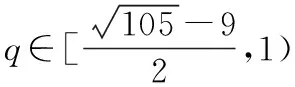
【考查目標】

本題考查隨機變量的分布列及確定目標下的概率等相關知識，同時考查了數列的遞推性質，數學歸納法的思想以及“非線性規劃”等一系列知識.考查了運算求解能力，數據分析以及數學建模等能力，落實了數據分析、邏輯推理等數學核心素養.

【名師指導】

(1)先確定n的取值，然后確定X的取值，求出其概率，進而求得分布列;(2)設G(m)≥G(1)求出p與q的關系，再利用“線性規劃”的思想考慮如下：根據兩個條件，可得點(p,q)的可行域：結合q的取值范圍求證.

【解題思路】

(1)當n=1時，X的取值可能為0,1,2,

當n=2時，X的取值可能為0,1,2,3,4,

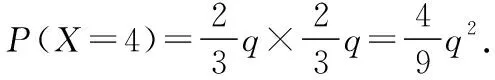
X01234P(1-13p-23q)22p3(1-13p-23q)4q3(1-13p-23q)49pq49q2

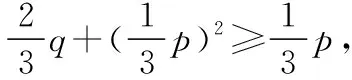
不妨設當k≤m時，G(k)≥G(1)成立，現考慮k=m+1時的情況;

對于G(m+1)，其值為G(m+1)=G(m)G(1)+G(m-1)G(2)；

令G(m+1)=G(m)G(1)+G(m-1)G(2)≥G(1)，根據假設G(m)≥G(1)，G(m-1)≥G(1)，

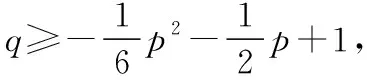
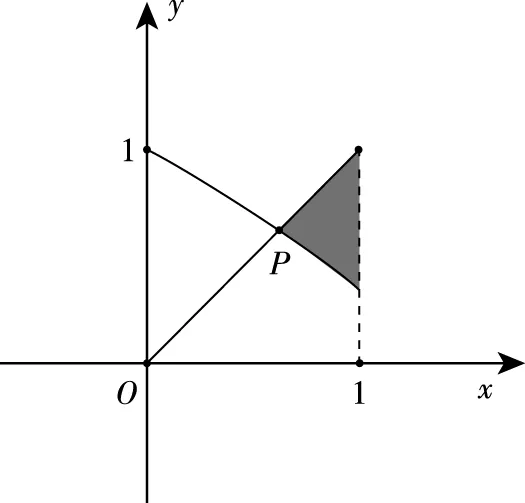
圖1

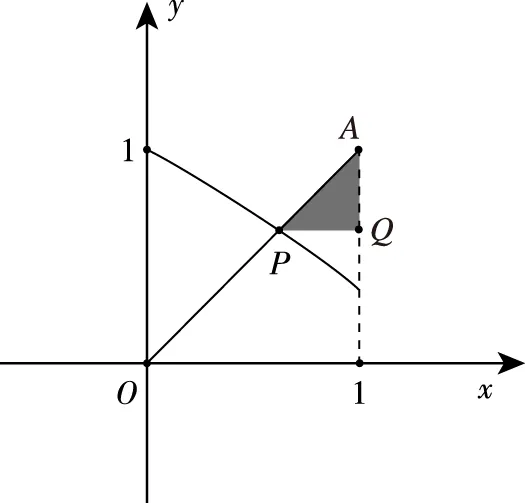
圖2

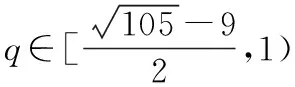
3.【研發題】

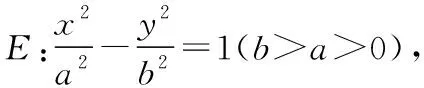
(1)求雙曲線E的方程;

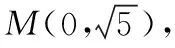
問題：是否存在過右焦點的直線與雙曲線E的右支相交于A,B兩點，________，使得∠AMB為直角？

【考查目標】

本題以圓錐曲線為背景，考查直線與雙曲線位置關系的問題，考查數學運算、邏輯推理的數學核心素養.

【名師指導】

【解題思路】

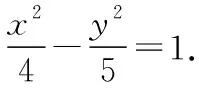
(2)方案①：令A(x1,y1),B(x2,y2)，

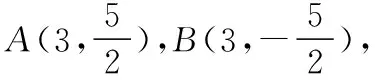
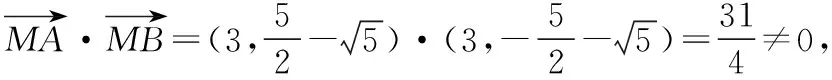
若直線AB與x軸不垂直，設直線AB的方程為y=kx-3k(k≠0)，

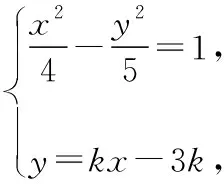
可得 (5-4k2)x2+24k2x-4(9k2+5)=0，Δ>0

由題意可知A，B兩點都在雙曲線的右支上，

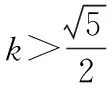
因為∠AMB為直角，所以AM⊥BM,

=0,

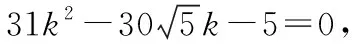
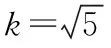
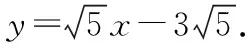
方案②：令A(x1,y1),B(x2,y2),

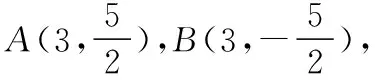
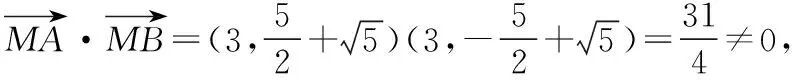
若直線AB與x軸不垂直，設直線AB的方程為y=kx-3k(k≠0),

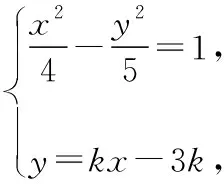
可得(5-4k2)x2+24k2x-4(9k2+5)=0,Δ>0，

由題意可知A,B兩點都在雙曲線的右支上,

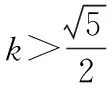
因為∠AMB為直角，所以AM⊥BM,

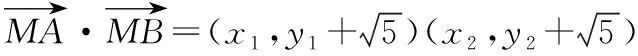
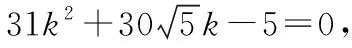
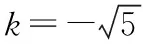
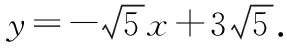
方案③：令A(x1,y1),B(x2,y2),

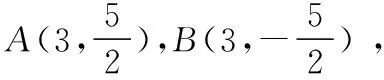
所以直線AB的方程為x=3.

若直線AB與x軸不垂直，設直線AB的方程為y=kx-3k(k≠0),

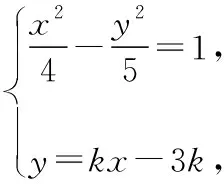
可得(5-4k2)x2+24k2x-4(9k2+5)=0.

由題意可知A,B兩點都在雙曲線的右支上,

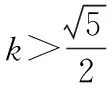
因為∠AMB為直角，所以AM⊥BM,