改進的灰狼算法及其在運動體控制中的應用

趙鑫 李文

摘要：針對基本灰狼算法因早收斂陷入局部最優的問題，提出了一種通過在解空間均勻分布搜索個體的改進灰狼算法，將其應用在復雜、高維、時變的運動體非線性控制系統中。該方法兼顧了優化算法的全局勘探和局部開采能力，利用MATLAB對運動體系統近似模型進行了仿真分析，結果表明算法在保證控制系統穩定性的基礎上，提高了控制器的動靜態性能，具有較好的工程應用前景。

關鍵詞：運動體控制;灰狼優化算法;MATLAB

中圖分類號：TP273? ? ?文獻標識碼：A

文章編號：1009-3044（2021）27-0001-02

Abstract： Aiming at the problem that the basic Gray Wolf algorithm falls into local optimum due to early convergence， an improved gray wolf algorithm is proposed by searching individuals uniformly in the solution space， which is applied to the complex， high-dimensional， time-varying nonlinear control system of moving body. This method takes into account the global exploration and local mining ability of the optimization algorithm， and uses MATLAB to simulate and analyze the approximate model of the moving body system. The results show that the algorithm improves the dynamic and static performance of the controller on the basis of ensuring the stability of the control system， and has a good engineering application prospect.

Key words： Moving object control; Gray wolf optimization algorithm; MATLAB

1 引言

近年來，群智能算法在多目標優化應用中，取得了豐碩的理論研究及應用成果[1-4]。GWO是源于灰狼群體的捕食行為而提出的群智能算法，該算法已廣泛應用于工業眾多領域。

然而，基本GWO算法與眾多群智能算法一樣存在易早熟收斂等問題。因此，對基本GWO算法進行改進并結合具體應用十分必要，本文提出了一種改進GWO算法，綜合考慮算法的全局和局部優化能力;應用在運動體控制器PID參數的整定中，通過MATLAB實現算法，仿真顯示其具有較好的全局尋優能力。

2 GWO算法原理

2.1 基本的GWO算法

灰狼群體中按等級機制可分為α狼、β狼、δ狼和ω狼，捕獵時，其他個體在α狼的帶領下對獵物圍攻。定義獵物的位置為優化問題的全局最優解。式（1）-（3）是灰狼接近并包圍獵物的描述：

2.2 改進的GWO算法

2.2.1 種群佳點集初始化

2.2.2 非線性收斂因子

2.2.3 算法優化流程圖

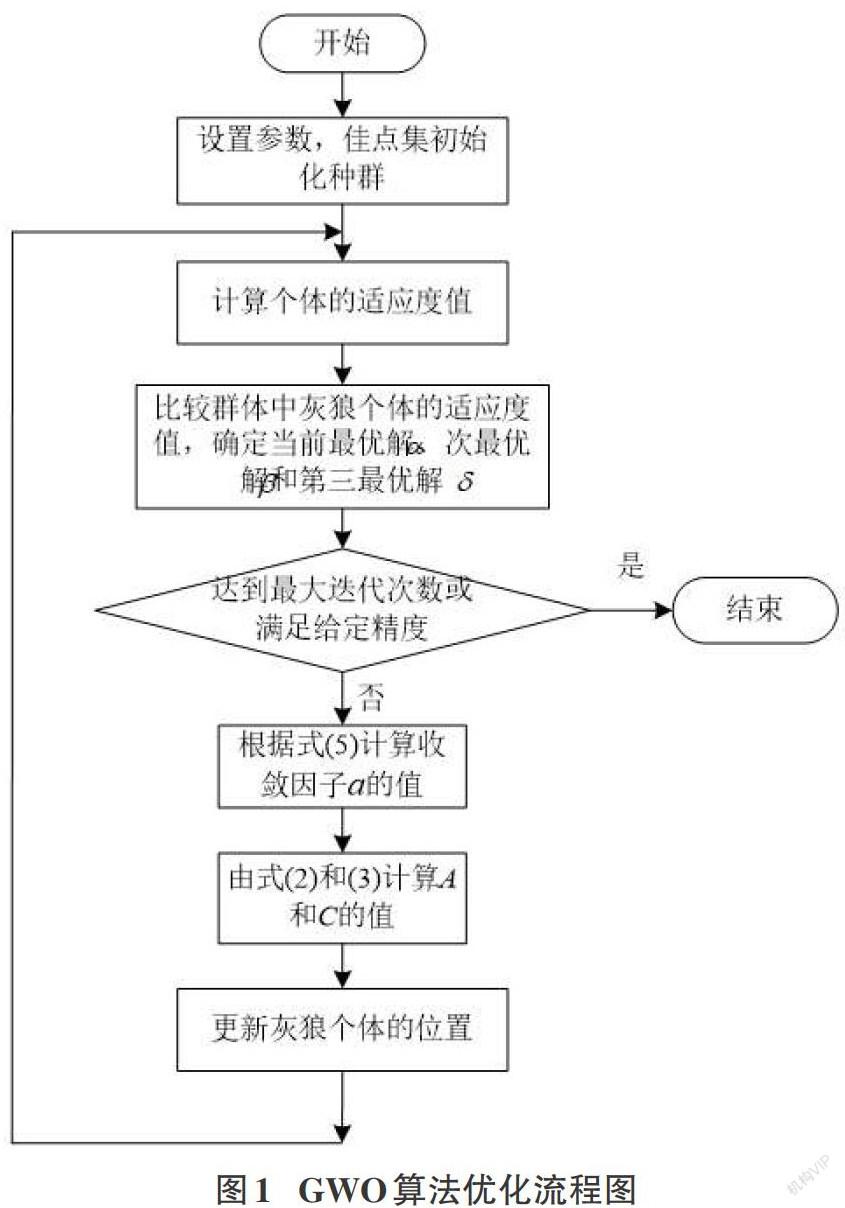
改進GWO算法優化流程圖如圖1所示。

3 改進GWO算法PID參數整定

3.1 PID參數整定思想

基于GWO算法的控制器系統原理結構如圖2所示：

3.2 整定PID參數步驟

改進PSO算法最優參數整定步驟如下：

① 初始化：設定參數;佳點集初始化種群。

② 計算灰狼個體的適應度值。

③ 比較并更新各灰狼個體的適應度值及全局最優位置。

④ 判斷未到上限迭代次數，即轉到⑤，否則結束尋優。

⑥ 根據（2）、（3）計算A、C的值。

⑦ 更新個體位置，進入下一次迭代。

4 仿真試驗分析

4.1 系統仿真

根據文獻[5]中的系統模型為：

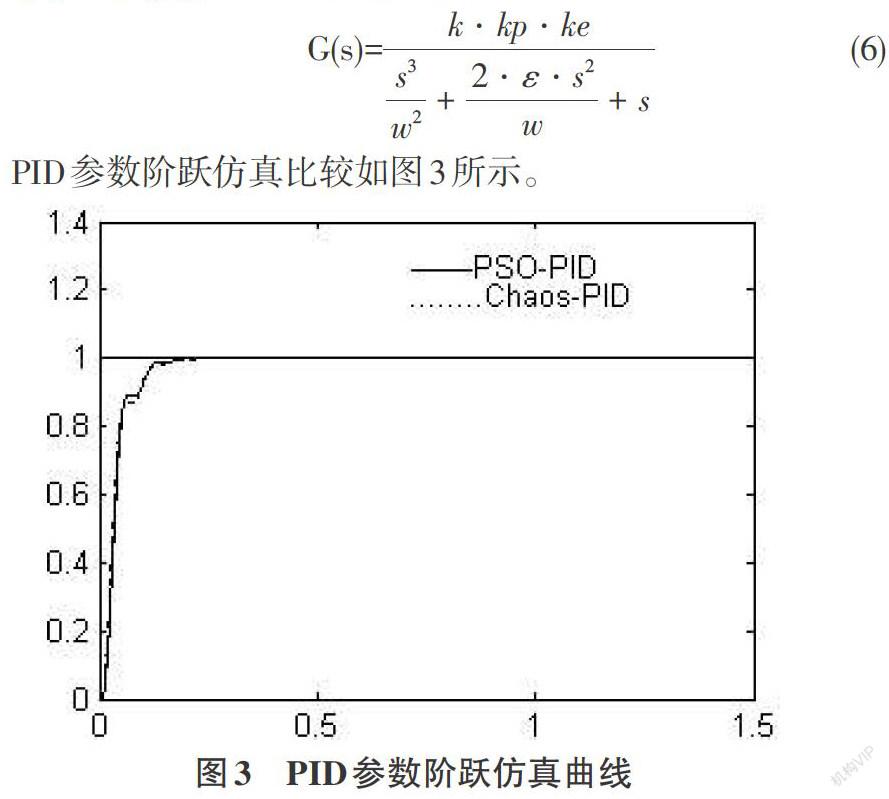
PID參數階躍仿真比較如圖3所示。

4.2 仿真分析比較

仿真結果表明GWO算法保證參數優化效果且效率高、穩定性強，有效地實現了控制器參數的全局優化，滿足工程應用實際。

5 結束語

針對傳統算法的普遍問題，改進了GWO算法并應用到運動控制系統中，試驗仿真表明改進的灰狼算法能適應復雜工業過程的參數優化。

參考文獻：

[1] 劉宏達，李殿璞，馬忠麗.基于多種群搜索策略粒子群算法的艦船消磁優化[J].儀器儀表學報，2006，27（S1）：861-863.

[2] 張偉，師奕兵，周龍甫，等.基于改進粒子群算法的小波神經網絡分類器[J].儀器儀表學報，2010，31（10）：2203-2209.

[3] 薛堯予，王建林，于濤，等.基于改進PSO算法的發酵過程模型參數估計[J].儀器儀表學報，2010，31（1）：178-182.

[4] 樸海國，王志新，張華強.基于合作粒子群算法的PID神經網絡非線性控制系統[J].控制理論與應用，2009，26（12）：1317-1324.

[5] 歐青立，李文，邱昭亮.攤鋪機行駛系統控制器PID參數的混沌優化[J].電子測量與儀器學報，2007，21（6）：85-88.

【通聯編輯：梁書】