平面近場聲全息中指數(shù)濾波器窗函數(shù)設(shè)計優(yōu)化

趙 晨，馮丹平，楊明明，高守勇

（91388部隊95分隊，廣東 湛江 524022）

0 引 言

近場聲全息技術(shù)（Near-field Acoustical Holography,NAH）是噪聲源識別、定位、分析的一項重要技術(shù)。其基本原理是通過測量近場全息面的聲場數(shù)據(jù)（如聲壓、振速、聲強等），采用一定的近場聲全息算法，反演重建聲源面聲場信息或者預(yù)測遠場輻射聲場信息[1]。根據(jù)測量面形狀的不同，近場聲全息技術(shù)分為平面近場聲全息、柱面近場聲全息和球面近場聲全息[2-5]。其中基于聲壓測量的平面近場聲全息技術(shù)，對于大型目標的噪聲源分析更為適用，并已經(jīng)應(yīng)用于實際測量工作中。

平面近場聲全息算法一直是聲學(xué)領(lǐng)域研究的熱點。常用平面近場聲全息算法所采用的基本方法包括空間二維傅里葉變換法、邊界元法、等效源法、統(tǒng)計最優(yōu)法等[6-10]。基于空間二維傅里葉變換法的近場聲全息（Near-Field Acoustic Holography Based on Spatial Two-Dimensional Fourier Transform,SFT-NAH）算法是近場聲全息算法中的一種典型算法，通過將全息面上聲壓進行空間二維傅里葉變換再乘以格林函數(shù)，最后進行空間二維傅里葉逆變換得到重建面或者預(yù)測面聲場信息。相比較其他方法，空間二維傅里葉變換法具有算法簡單、不需要占用較大內(nèi)存和計算速度快等優(yōu)點。

采用空間二維傅里葉變換法進行近場聲全息重建時，由于環(huán)境噪聲、系統(tǒng)誤差等因素的影響，對重建過程有重要影響的高波數(shù)域的倏逝波成分很容易被各類噪聲誤差淹沒，導(dǎo)致重建結(jié)果產(chǎn)生較大誤差。因此重建過程中必須進行波數(shù)域的低通濾波，指數(shù)濾波器是基于空間二維傅里葉變換法的近場聲全息算法中常用的濾波方法[11]。該方法中有兩個關(guān)鍵參數(shù)，分別是指數(shù)濾波器截止波數(shù)和指數(shù)濾波器窗函數(shù)陡度系數(shù)。這兩個關(guān)鍵參數(shù)如果設(shè)置不合理就會嚴重影響指數(shù)濾波器濾波效果，進而影響近場聲全息算法聲場重建效果。因此對其進行設(shè)計優(yōu)化，對于提高聲全息算法的重建精度和分辨率具有重要意義。

本文以水下聲全息技術(shù)應(yīng)用為背景，以大孔徑近場聲全息面為分析模型，重點分析對應(yīng)不同聲源頻率，指數(shù)濾波器窗函數(shù)及截止波數(shù)的取值對聲全息重建誤差的影響。相鄰兩聲源相干引起的分辨率誤差是近場聲全息重建誤差的一個主要來源，有效降低該誤差是提高近場聲全息算法精度的一項重要工作，因此選取兩個相鄰聲源作為檢測的對象，針對基于空間二維傅里葉變換法的近場聲全息算法中指數(shù)濾波器的截止波數(shù)和窗函數(shù)陡度系數(shù)這兩個關(guān)鍵參數(shù)，采用最小二乘法進行了設(shè)計優(yōu)化。優(yōu)化結(jié)果表明，有效提高了基于空間二維傅里葉變換法的近場聲全息算法的重建精度和分辨率。

1 基于空間二維傅里葉變換法的近場聲全息算法基本原理

由水聲傳播基本理論可知，在理想流體介質(zhì)中，不依賴于時間變量的穩(wěn)態(tài)聲場的亥姆霍茲（Helmholtz）方程為

在狄利克雷（Dirichlet）邊界條件下，格林函數(shù)為

對式（2）兩邊進行空間二維傅里葉變換，可得：

FFT-NAH的基本思想是由全息面聲壓分布矩陣對其做空間二維傅里葉變換，將其轉(zhuǎn)化到波數(shù)域，經(jīng)波數(shù)域濾波后乘以對應(yīng)的格林函數(shù)矩陣，便可得到空間二維傅里葉變換后的重建面的聲壓分布矩陣，對其做空間二維傅里葉逆變換即可得到重建面聲壓分布。

2 指數(shù)濾波器

在近場聲全息理論中，當(dāng)全息面聲壓進行二維傅里葉變換后將其與對應(yīng)指數(shù)濾波器相乘，以此來進行波數(shù)域濾波，是提高近場聲全息算法重建精度的一種有效手段。本文在計算過程中首先對全息面聲壓數(shù)據(jù)進行二維傅里葉變換，然后與對應(yīng)指數(shù)濾波器相乘進行波數(shù)域濾波，最后進行二維傅里葉逆變換得到重建面聲壓分布。

基于空間二維傅里葉變換法的近場聲全息算法中常用的指數(shù)濾波器計算公式為[11]

由式（5）可以看出，指數(shù)濾波器的設(shè)計有兩個關(guān)鍵參數(shù)，分別是窗函數(shù)的陡度系數(shù)α和濾波器的截止波數(shù)kc。已有研究中，通常情況下指數(shù)濾波器窗函數(shù)陡度系數(shù)α的取值范圍為0.1～0.2，指數(shù)濾波器截止波數(shù)kc經(jīng)驗公式為：kc=0.6π/Δ，Δ為全息面上的測量間隔，對于本文研究工作具有一定的參考意義。本文將針對窗函數(shù)的陡度系數(shù)α和濾波器的截止波數(shù)kc這兩個關(guān)鍵參數(shù)的優(yōu)化設(shè)計，采用最小二乘法分別進行仿真分析。

3 仿真分析

3.1 點聲源及全息測量面模型建立

以頻率為1 kHz、聲源半徑為0.01 m和間距為1.5 m的兩個模擬點聲源為聲源模型進行仿真分析，結(jié)果如圖1所示。同時，建立規(guī)模為50 m×50 m、測量間隔分別為 50 m和 255 m、距離聲源中心面1 m的全息測量面仿真模型。以均勻分布噪聲模擬環(huán)境噪聲等各種噪聲，模擬信噪比為20 dB時仿真全息測量面的測量效果如圖2所示。

圖1 模擬點聲源聲壓傳播圖Fig.1 Sound pressure propagation diagram of simulated point sound source

圖2 模擬全息測量面測得聲壓分布圖Fig.2 Sound pressure distribution diagram measured by simulated holographic measuring surface

通常情況下濾波器窗函數(shù)陡度系數(shù)α的取值范圍為0.1～0.2，濾波器截止波數(shù)kc=0.6π/Δ，但通過仿真分析發(fā)現(xiàn)，當(dāng)聲源頻率不同時，選擇不同的濾波器窗函數(shù)陡度系數(shù)α和濾波器截止波數(shù)kc會有更優(yōu)的反演效果。例如，當(dāng)聲源頻率為1 kHz，時若α=0.12，kc=0.6π/Δ，則反演點聲源聲壓傳播圖如圖3所示。當(dāng)聲源頻率為1 kHz，時若α=0.06，kc=0.3π/Δ，則反演點聲源聲壓傳播圖如圖4所示。

圖3 聲源頻率為1 kHz，α=0.12，kc=0.6π/?，反演點聲源聲壓傳播圖Fig.3 The inversed sound pressure propagation diagram of 1 kHz point source for α=0.12 and kc=0.6π/?

圖4 聲源頻率為1 kHz，α=0.06，kc=0.3π/?，反演點聲源聲壓傳播圖Fig.4 The inversed sound pressure propagation diagram of 1 kHz point source for α=0.062 and kc=0.3π/?

3.2 指數(shù)濾波器參數(shù)設(shè)計分析

定義p1為模擬點聲源聲壓幅值分布，p2為反演點聲源聲壓幅值分布。定義點聲源聲壓反演結(jié)果的幅值誤差為[12]

3.2.1 濾波器截止波數(shù)設(shè)計分析

α值為0.12時，分別取kcΔ/π的值為0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9，對相應(yīng)的反演聲源面聲壓分布效果對比分析如表1所示。

表1 α=0.12 時，kc?/π 與 E 對應(yīng)關(guān)系Table 1 The correspondence between kcΔ/π and E,when α=0.12

α值為0.15時，分別取kcΔ/π的值為0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9，對相應(yīng)的反演聲源面聲壓分布效果對比分析如表2所示。

表2 α=0.15時，kc?/π與E對應(yīng)關(guān)系Table 2 The correspondence between kc?/π and E,when α=0.15

α值為0.18時，分別取 kcΔ /π的值為0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9，對相應(yīng)的反演聲源面聲壓分布效果對比分析如表3所示。

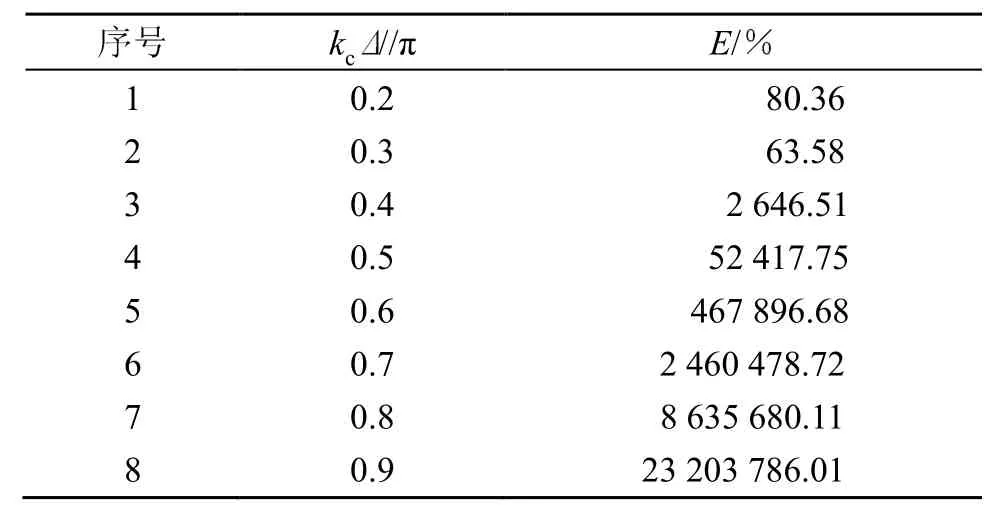
表3 α=0.18時，kc?/π與E對應(yīng)關(guān)系Table 3 The correspondence between kc?/π and E,when α=0.18

從表 1、表 2和表 3中不難發(fā)現(xiàn)，當(dāng)α值為0.12、0.15、0.18時，改變kcΔ/π的值，三種情況下均是當(dāng) kcΔ/π的值為0.3時，反演效果相對較好。

3.2.2 窗函數(shù)陡度系數(shù)設(shè)計分析

當(dāng)kcΔ/π的值為0.3時，分別取α值為0.02、0.04、0.06、0.08、0.1、0.12、0.14、0.16、0.18、0.2，對相應(yīng)的反演聲源面聲壓分布效果對比分析如表4所示。

表4 kc?/π=0.3時，α與E對應(yīng)關(guān)系Table 4 The correspondence between α and E,when kc?/π=0.3

kc/Δπ的值為0.2時，分別取α值為0.02、0.04、0.06、0.08、0.1、0.12、0.14、0.16、0.18、0.2、0.25、0.3、0.35，如表5所示，對相應(yīng)的反演聲源面聲壓分布效果進行對比分析。

表5 kc?/π=0.2時，α與E對應(yīng)關(guān)系Table 5 The of correspondence between α and E,when kc?/π=0.2

kc/Δπ的值為0.4時，分別取α值為0.02、0.04、0.06、0.08、0.1、0.12、0.14、0.16、0.18、0.2，對相應(yīng)的反演聲源面聲壓分布效果對比分析如表6所示。

表6 kc?/π=0.4時，α與E對應(yīng)關(guān)系Table 6 The of correspondence between α and E,when kc?/π=0.4

通常情況下α的取值范圍為0.1～0.2，表4和表6中在對應(yīng)分析條件下，當(dāng)α的取值在0.02～0.2中已找到最優(yōu)取值，而在表5中，α取到了0.35，當(dāng)α=0.3時E出現(xiàn)最小值，這一結(jié)果說明針對不同的全息面參數(shù)設(shè)計、測量環(huán)境以及不同的聲源頻率，指數(shù)濾波器窗函數(shù)陡度系數(shù)的最優(yōu)取值并不局限于0.1～0.2。

從表1～6中數(shù)據(jù)不難看出，kcΔ/π的值為0.3、α的值為0.06時，反演效果最好。且通過對比可以看出，相比較窗函數(shù)陡度系數(shù)α的取值變化，濾波器截止波數(shù)kc的取值變化對反演效果影響更加明顯。

3.3 指數(shù)濾波器參數(shù)設(shè)計與聲源頻率對應(yīng)關(guān)系分析

通過進一步仿真分析，可得到在相同點聲源面模型和全息面模型中，對應(yīng)不同的聲源頻率時，要取得最優(yōu)重建效果，相對應(yīng)的濾波器窗函數(shù)陡度系數(shù)α和濾波器截止波數(shù)kc取值如表7所示。

表7 對應(yīng)不同聲源頻率時kc?/π值，α與E對應(yīng)關(guān)系Table 7 The correspondence of kc?/π,α and E for the sound sources of different frequencies

從表 7中數(shù)據(jù)可以看出，聲源頻率在 100～1 500 Hz之間時，隨著聲源頻率的增加，指數(shù)濾波器窗函數(shù)的陡度系數(shù)α的最優(yōu)設(shè)置逐漸減小，濾波器截止波數(shù)kc的最優(yōu)設(shè)置逐漸增大。

4 結(jié) 論

本文對平面近場聲全息中指數(shù)濾波器窗函數(shù)設(shè)計進行了分析和優(yōu)化，建立了頻率為1 kHz、聲源半徑為0.01 m和間距為1.5 m的兩個模擬點聲源模型，以及規(guī)模為50 m×50 m、測量間隔分別為50 m、255 m和與聲源中心面距離為1 m的全息測量面仿真模型。同時以均勻分布噪聲模擬環(huán)境噪聲。通過分析濾波器截止波數(shù)kc和濾波器窗函數(shù)陡度系數(shù)α的取值對反演誤差的影響，找出了kcΔ/π的值為0.3、α的值為0.06時，采用指數(shù)濾波器濾波后的反演效果最好。相比較窗函數(shù)陡度系數(shù)α的取值變化，濾波器截止波數(shù)kc的取值變化對反演效果影響更加明顯。同時發(fā)現(xiàn)，聲源頻率在100～1 500 Hz之間時，隨著聲源頻率的增加，指數(shù)濾波器窗函數(shù)的陡度系數(shù)α的最優(yōu)設(shè)置逐漸減小，濾波器截止波數(shù)kc的最優(yōu)設(shè)置逐漸增大。總結(jié)了聲源頻率在100～1 500 Hz之間時，對應(yīng)不同聲源頻率，要取得最優(yōu)重建效果，濾波器窗函數(shù)陡度系數(shù)α和濾波器截止波數(shù)kc的最優(yōu)取值，對平面近場聲全息中指數(shù)濾波器窗函數(shù)的設(shè)計優(yōu)化具有重要意義。