具有毒素作用和自由邊界的種群模型解的爆破
張泰年,雒志學
(1. 蘭州交通大學 環境與市政工程學院,蘭州 730070;2. 蘭州交通大學 數理學院,蘭州 730070)
隨著現代工業和農業的迅速發展,生態問題日益突出,毒素的侵襲極易發生,澳大利亞叢林大火,東非蝗災,非典(SARS),埃博拉病毒,禽流感病毒,甲型H1N1流感,新冠肺炎等,這每一個現象正威脅著生態平衡,對人類和其它生物的生存造成了嚴重危害.因此,研究毒素對生物種群的影響越來越重要.Hallam等[1-3]提出了用動力學方法研究生態毒理動力學的想法.他們提出具有毒素作用的種群模型,并研究了有毒物質入侵物種的持久性和絕滅性.從20世紀80年代起,人們對生態毒理學的問題才開始進行了深入研究,并且現在有大量關于生態毒理學問題的研究[4-6],人們密切關注有毒物質對環境中種群的影響.在數學生態學研究中,新種群或入侵種群的擴張是一個熱門話題,然而在這些模型中研究者均未考慮毒素對種群的影響.本文運用數學模型去描述和分析具有毒素作用的生物系統內部的機理,根據實際情況建立了數學模型,這在有效控制種群規模,預測種群變化趨勢,維持生態平衡,優化生態環境,防控流行病,抑制生物入侵以及生物資源合理開發利用等方面有著重大的生態學意義.
近年來,生物入侵的模擬已經吸引了專家們的廣泛注意,并且通過研究擴張前沿的傳播,人們對生物種群擴張的理解得到了明顯的改觀.入侵種群的擴張或者消失取決于初始時刻種群密度和區域的大小,也就是種群可能在有限區域上消失.基于以上原因,本文引入自由邊界問題來描述種群的擴張過程,自由邊界的引入成功地避開了上述缺陷,能夠使我們更好的利用數學模型描述種群的發展動態.自由邊界問題在科學、工程及工業生產中有著廣泛的應用,例如:美式期權定價問題、凝結血管附近肌肉中氧氣的減少、傷口愈合、種群遷徙問題等.2007年,Lin[7]研究了一類具有自由邊界的兩種群捕食模型,證明了古典解的存在唯一性,結果表明,所研究的問題是適定的,捕食者在有限時間內擴散到整個研究區域.2010年,Du等[8]研究了在一維空間中具有自由邊界擴散的Logistic模型,證明了該模型傳播-消失的二擇一性質,即該種群要么進入到新環境并穩定在平衡狀態,要么無法生存最終死亡,此外,當傳播發生時,擴張前沿會以恒定的速度移動,這種擴張速度是由原始模型推導出的橢圓問題唯一決定的.2011年,Du等[9]在文獻[8]的基礎上研究了在高維空間中具有自由邊界擴散的Logistic模型,證明了傳播-消失二擇一性質.此外,當傳播發生時,得到傳播速度的上確界和下確界,當時間趨于無窮時,這兩個界限接近于某個常數.更多的模型可參見文獻[10-16].受以上研究工作的啟發,本文討論了如下具有毒素影響的單種群模型的高維球對稱情形的自由邊界問題:
(1)
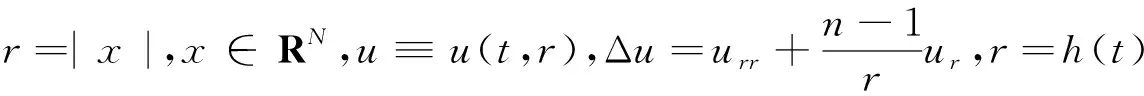
(2)
生物體內與環境中毒素的濃度c0,ce從系統(1)中解得
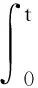
[(s-t)(g1+m)]dτ,
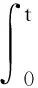
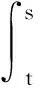
并且滿足
0≤c0(t)≤1,0≤ce(t)≤1,0≤t<+∞.
1 局部解的存在唯一性
在這一部分,本文運用壓縮映像原理來證明問題(1)的局部球對稱解的存在唯一性.
定理1.1對滿足式(2)的任意u0以及α∈(0,1),存在T>0使得問題(1)存在唯一解
(u,h)∈C(1+α)/2,1+α(DT)×C1+α/2([0,T]),
并且
‖u‖C(1+α)/2,1+α(DT)+‖h‖C1+α/2([0,T])≤C,
(3)
其中:DT={(t,r)∈R2∶t∈[0,T],r∈[0,h(t)]},C和T僅僅依賴于h0,α及‖u0‖C2([0,h0]).
證明類似于文獻[17],首先作變換將自由邊界拉直,令ζ(s)∈C3[0,+∞)滿足
作變換
(4)
由式(4)得到
(t,s)→(t,r),r=s+ζ(s)(h(t)-h0),0≤s<+∞,
而且
只要
上述變換x→y是從RN到RN的微分同胚,而s→r是從[0,+∞)到[0,+∞)的微分同胚.顯然,上述變換將自由邊界|x|=h(t)分別變成固定球面|y|=h0.直接計算得
如果令
u(t,r)=u(t,s+ζ(s)(h(t)-h0))=w(t,s),
則
ut=wt-h′(t)C(h(t),s)ws,
urr=A(h(t),s)wss+B(h(t),s)ws,
所以自由邊界問題(1)轉化為
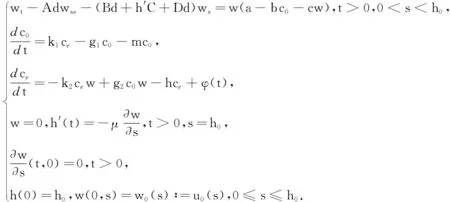
(5)
其中:A=A(h(t),s),B=(h(t),s),C=C(h(t),s),D=D(h(t),s).
VT={w∈C([0,T]×[0,h0])∶w(0,s)=u0(s),‖w-u0‖C([0,T]×[0,h0])≤1},
HT={h∈C1([0,T])∶h(0)=h0,h′(0)=h*,‖h′-h*‖C([0,T])≤1}.
注意到對h1,h2∈HT,由于h1(0)=h2(0)=h0,有
(6)
因此∑T∶=VT×HT在距離
d((w1,h1),(w2,h2))=‖w1-w2‖C([0,T]×[0,h0])+
是完備的度量空間.
接下來將運用壓縮映像原理[18]證明解的局部存在唯一性.首先,對任意給定的(w,h)∈VT×HT,根據T的選擇,有
因此變換(t,r)→(t,s)的定義是合理的.根據拋物方程標準的Lp理論以及Sobolev嵌入定理可知,對于任意的(w,h)∈∑T,下列初邊值問題
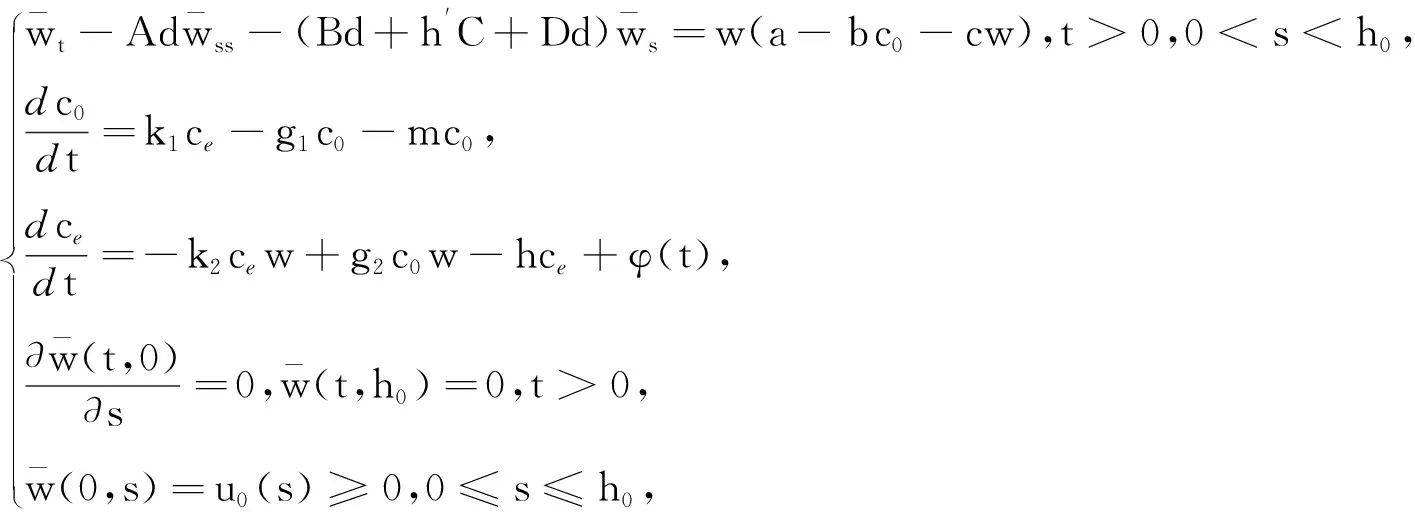
(7)
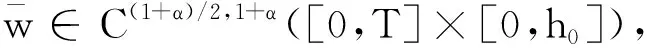
C1,
(8)
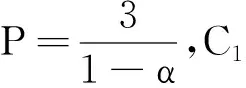
定義
(9)
有
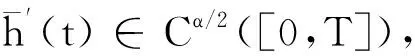
(10)
定義映射F∶∑T→C([0,T]×[0,h0])×C1([0,T])如下
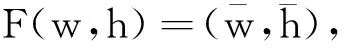
顯然,(w,h)∈∑T是F的一個不動點,當且僅當(w,h)是問題(5)的解.
由估計式(8)和(10),有

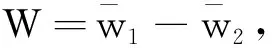
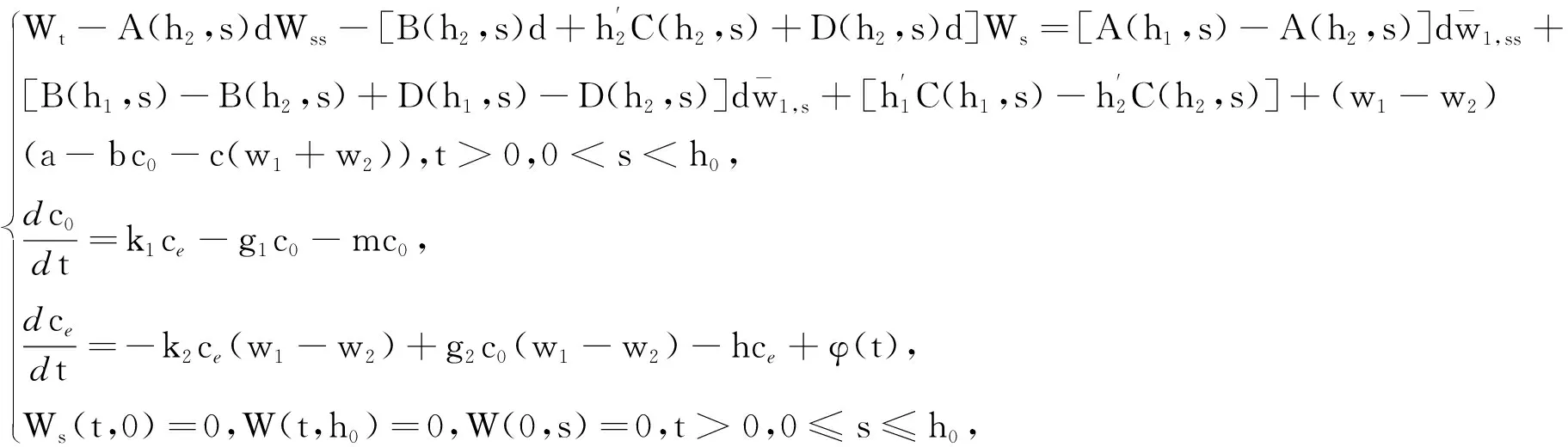
根據拋物方程的Lp估計以及Sobolev嵌入定理,得到
C3(‖w1-w2‖C([0,T]×[0,h0])+‖h1-h2‖C1([0,T])),
(11)
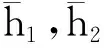
(12)
聯立不等式(6),(11),(12),并假設T≤1,得到
其中C4依賴于C3和μ.于是對
有:
因此,對于這樣的T,F就是一個壓縮映射.故由壓縮映像原理知F有唯一的不動點(w,h)∈∑T滿足F(w,h)=(w,h).這說明(w,h)是問題(5)的唯一解,也就是說,(u,h)是問題(1)的唯一解,并且由Schauder估計,可以提高此解的正則性
u∈C1+α/2,2+α((0,T]×[0,h0]),h(t)∈C1+α/2((0,T]),
換言之,(u(t,r),h(t))是問題(1)唯一的局部古典解.故定理得證.
2 爆破解
根據定理1.1,存在T使得問題(1)的解在[0,T]存在且唯一,且解的區間可延拓到[0,Tmax),其中Tmax=Tmax(u0)∈(0,+∞]為解的最大存在時間,為了得到解的爆破結果,首先建立下面引理.
引理2.1設(u,h)為問題(1)在t∈(0,T0)的解,且在(0,T0)×[0,h(t))上成立u(t,r)≤M1,其中T0∈(0,+∞],則存在于T0無關的常數M2使得
0 證明應用Hopf引理,得到 再結合Stefan條件,可推出問題(1)的自由邊界的單調性 接下來證明h′(t)≤M2.對任意t∈(0,T0)成立,其中M2與T0無關.為此定義 ΩM∶={(t,x)∶h(t)-M-1 并構造如下輔助函數 w(t,r)∶=M1[2M(h(t)-r)-M2(h(t)-r)2], 選取M使得w(t,r)≥u(t,r)在ΩM中成立. 當(t,r)∈ΩM時,直接計算得 wt=2M1Mh′(t)[1-M(h(t)-r)]≥0, wr=-2M1M[1-M(h(t)-r)]≤0, wrr=-2M1M2, u(a-bc0-cu)≤aM1. wt-dΔw≥2dM1M2≥aM1≥u(a-bc0-cu). 此外 w(t,h(t)-M-1)=M1≥u(t,h(t)-M-1),w(t,h(t))=0=u(t,h(t)). 由于 所以w(0,r)≥u0(r),對w-u在Ω上應用極值原理可得u(t,r)≤w(t,r),(t,r)∈Ω,進而 故引理得證. 定理2.1問題(1)的解存在且唯一,并且可以延拓到[0,Tmax),其中Tmax≤∞.如果Tmax<∞,則有下列關系成立 此時,稱u(t,r)在有限時刻爆破. 證明運用Zorn引理并根據唯一性可知,存在Tmax使得[0,Tmax)為解的最大存在區間.由定理1.1可知Tmax>0.因此,只需證明當Tmax<∞時,有 用反證法證明.假設Tmax<∞,由引理2.1可知存在不依賴Tmax的M1和M2使得對于(t,r)∈[0,Tmax)×[0,h(t)],有 0≤u(t,r)≤M1,h0≤h(t)≤h0+M2t,0≤h′(t)≤M2. ‖u(t,·)‖C2([0,h(t)])≤M3,t∈[δ0,Tmax). 本文主要研究了一類具有毒素作用的高維情形下的種群模型的自由邊界問題,所研究的區域是徑向對稱的.隨后給出了此類問題解的性質,即初值充分大時,解在有限時刻爆破一定發生.通過加入毒素對種群的影響,推廣了一般的具有毒素作用和自由邊界的生物種群模型.
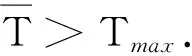
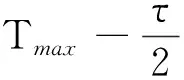
3 小結

