基于灰關聯理論的既有隧道襯砌背后空洞對襯砌受力的影響分析

孫壽榜，嚴松宏，剡永偉

(蘭州交通大學 土木工程學院，蘭州 730070)

隨著經濟的快速發展，我國已成為世界上隧道數量最多、建設速度最快的國家，施工技術已達世界領先水平[1]，與此同時，部分運營隧道由于復雜的地質條件、地形條件、以及當時施工不當等原因，隧道襯砌裂縫、襯砌后空洞、二襯厚度不足等病害也越來越多[2-3].襯砌背后空洞是運營隧道中最主要病害之一，它可能導致襯砌邊緣發生裂紋、開裂、失穩、跌落甚至突然坍塌[4-6].由于空洞在襯砌后面形成，所以在襯砌發生嚴重損傷(通常是嚴重開裂、剝落甚至失效)之前，很難發現空洞.常規檢查空洞的方法是用錘敲擊襯砌表面，然后識別空洞，然而隨著科技的進步，探地雷達(GPR)為隧道襯砌質量評價提供了一種相對方便快捷的無損檢測手段，探地雷達法已在隧道襯砌空洞、襯砌厚度、圍巖溶洞等病害檢測中得到了廣泛的應用[7-10].穆偉[11]利用探地雷達對襯砌背后空洞進行了檢測，對襯砌質量缺陷地質雷達波形圖進行解譯及分析并總結出隧道襯砌空洞缺陷的幾種典型地質雷達波形特征.楊睿等[12]采用探地雷達檢測襯砌背后空洞，并進行鉆孔取芯驗證，結果表明探地雷達用于空洞檢測可行且具有較高的可信度.既有隧道存在空洞會對襯砌的軸力和彎矩產生不利影響，這也是襯砌開裂及失穩的根本原因.Yasuda等[13]給出了基于平面應變假設條件下，深埋圓形隧道襯砌背后空洞的彈性解，計算結果表明，空洞的存在使襯砌的應力狀態由軸向推力變為彎矩狀態，空洞的存在導致襯砌應力集中，從而導致襯砌產生不良變形和應力.Meguid等[14]通過彈塑性有限元分析，研究了不同影響因素下空洞對襯砌軸力和彎矩的影響，空洞出現在隧道仰拱處，影響較為嚴重，彎矩符號從負改為正，襯砌可能出現開裂.崔文艷等[15]基于隧道襯砌后空洞對結構安全影響的模型試驗，通過數值分析，研究空洞在不同位置對隧道襯砌的力學行為的影響，通過對襯砌軸力和彎矩的分析，得出不同位置的空洞都會影響襯砌結構的安全性能，存在空洞的位置極易引起應力集中，襯砌破壞較為明顯.

本文借助探地雷達對既有隧道進行無損檢測并探明空洞的分布位置及大小，結合設計資料建立有限元數值模型，針對空洞對襯砌受力的影響進行研究.同時，引入灰色關聯理論，對由于空洞而產生的襯砌附加軸力和彎矩進行灰關聯分析.本研究為對后續隧道病害評價與綜合整治以及類似工程的設計提供參考.

1 現場檢測

對某既有隧道進行了無損檢測， 設置了五條測線，檢測采用SIR-3000型便攜式探地雷達，該型雷達數字化程度高、探測范圍廣、分辨率高，并且具有實時數據處理和成像能力,如圖1所示.

圖1 現場檢測圖Fig.1 On-site inspection map

雷達反射剖面如圖2所示,圖2(a)為襯砌與圍巖雷達反射剖面示意圖,空洞中一般存在空氣，圍巖、噴射混凝土和二襯與空氣的介電常數存在明顯差異，因此在時間剖面圖上，同相的雷達波錯斷并向上彎曲，并在混凝土和圍巖、空洞之間有明顯的界線.圖2(b)為空洞雷達反射剖面，當襯砌界面反射信號強，三振相明顯，在其下部仍有強反射界面信號，且兩組信號時程差較大，可判斷此處存在空洞.

通過現場檢測發現，在不同里程和隧道不同位置處襯砌界面反射信號強，三振相明顯，根據圖2(b)判斷襯砌背后存在大小不等的空洞，空洞的剖面形狀近似呈橢圓狀，深度主要分布在0.3～1.5 m，長度約是深度的2倍，與襯砌的距離主要分布在0～1.2 m，如圖3所示，此外，通過雷達反射剖面發現部分區段存在二襯厚度不足.

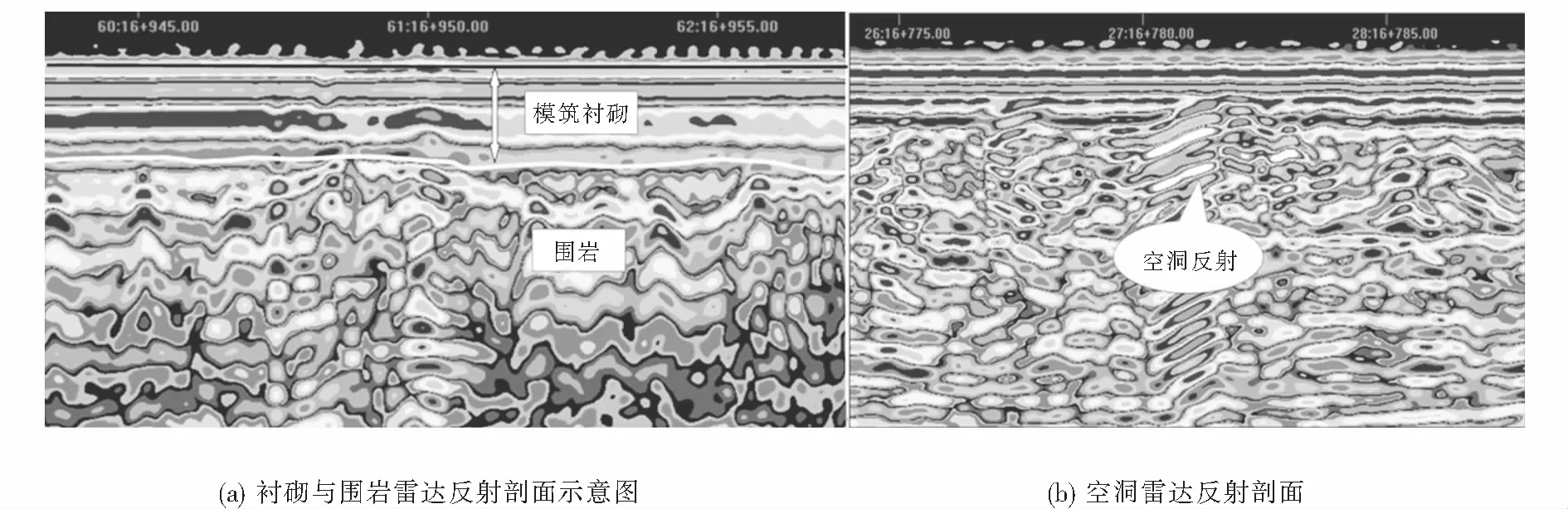
圖2 雷達反射剖面Fig.2 Radar reflection profile

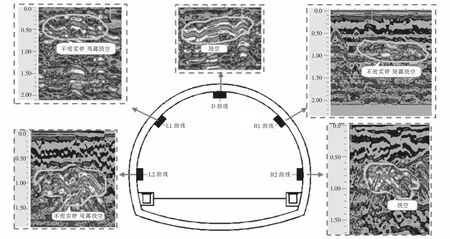
圖3 不同位置處空洞雷達反射剖面(單位:m)Fig.3 Radar reflection profiles of holes at different locations (unit:m)

2 數值分析

2.1 數值模型

根據現場檢測數據和設計資料，建立數值模型，計算采用“地層-結構”模型，模型頂部為自由邊界，兩側邊界為水平約束，底邊界豎向約束，二襯采用梁單元模擬.模擬計算分7步進行：① 初始應力場分布→② 位移清零→③ 隧道開挖→④ 施作初襯→⑤ 初襯硬化→⑥ 施作二襯→⑦ 出現空洞.襯砌背后空洞通過軟件中的鈍化單元功能實現.隧道數值模型如圖4所示，圖4(a)為沒有空洞時數值模型，圖4(b)為有空洞時數值模型.根據該隧道設計資料確定了圍巖和支護結構的相關物理力學參數，如表1所列.

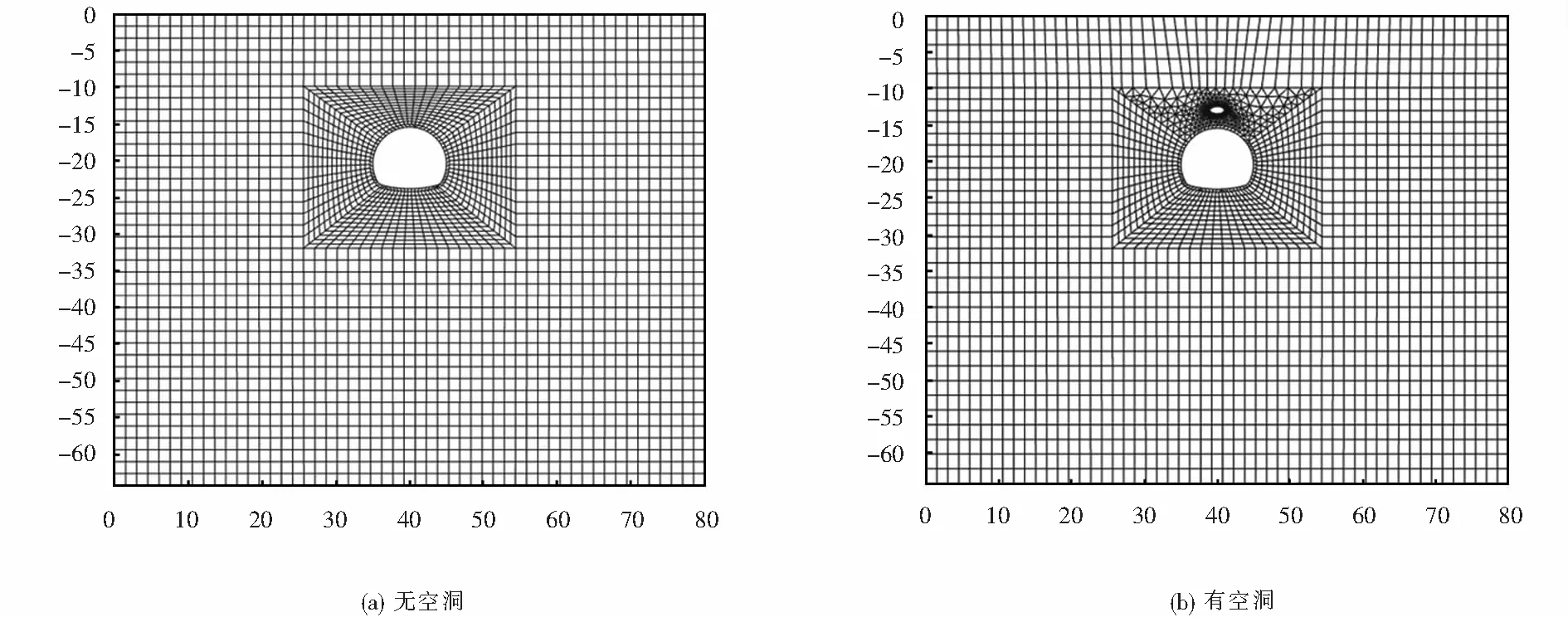
圖4 隧道數值模型(單位:m)Fig.4 Numerical model of the tunnel (unit:m)

表1 計算模型物理力學參數Tab.1 Physical and mechanical parameters of the computational model

2.2 結果分析

二襯內力分布如圖5所示.圖5(a)是施作二襯后軸力分布圖，從圖可以看出，軸力分布基本均勻，上部均為壓力，最大軸力為-45.444 kN，圖5(b)是出現空洞后軸力分布圖，很明顯看出，由于空洞的出現改變了軸力的分布，軸力主要集中分布在拱頂區域，最大軸力為-236.275 kN較未出現空洞時增加了約4.2倍.圖5(c)是施作二襯后彎矩分布圖，二次襯砌所受的最大正(內側受拉)、負(外側受拉)彎矩出現在拱頂和拱腰，分別為9.393 kN·m和-6.541 kN·m，圖5(d)是出現空洞后二襯彎矩分布圖，很明顯空洞的出現改變了彎矩分布，最大正負彎矩分別為10.674 kN·m，-7.544 kN·m，較(c)圖分別增加了13.6%和15.3%，甚至在拱頂出現了負彎矩，最大值為-5.241 kN·m.

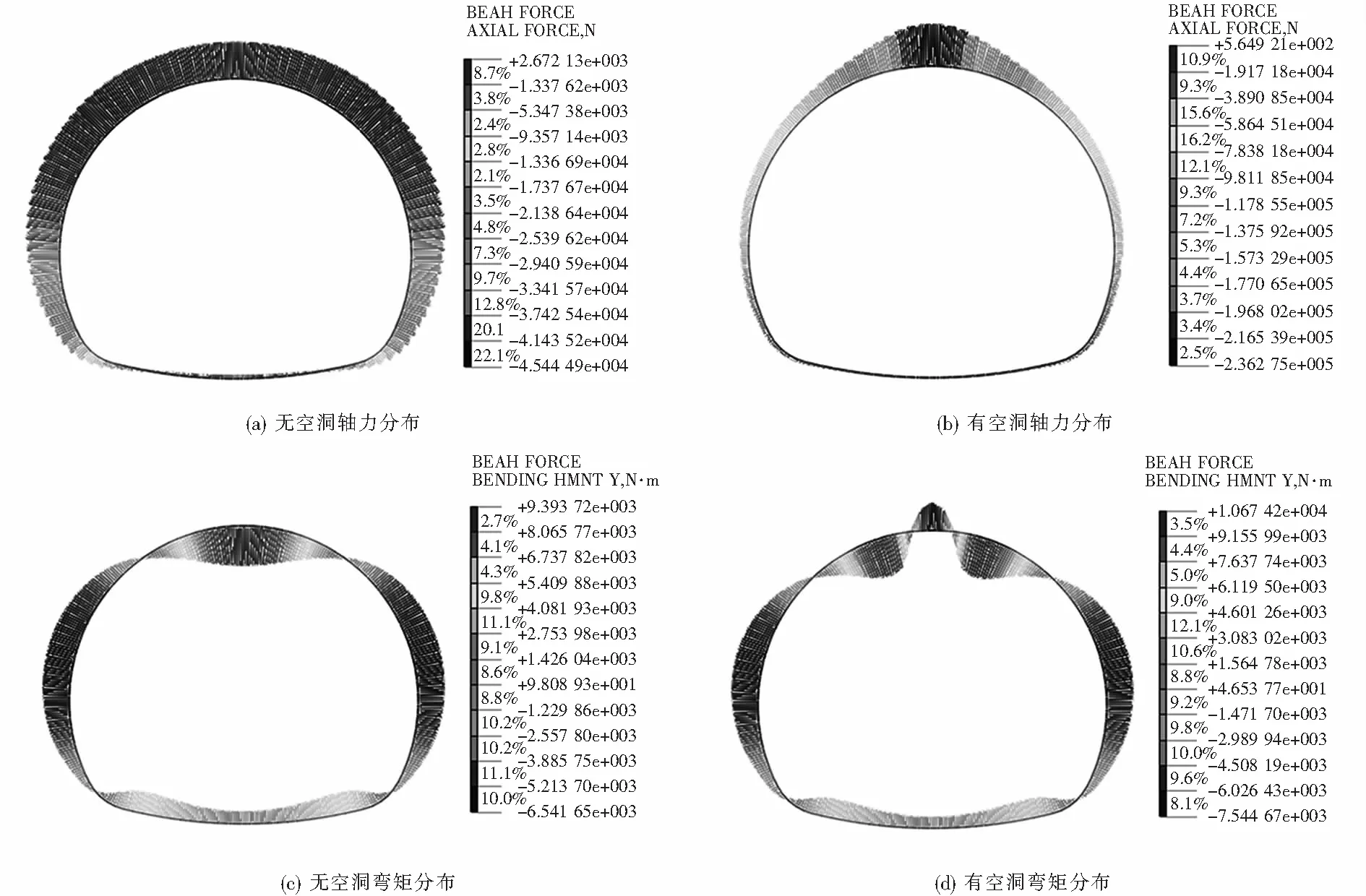
圖5 二襯內力分布Fig.5 Internal force distribution of the second lining

用數值分析第⑦步(出現空洞)內力分布減去第⑥步(施作二襯)內力分布，得到了二襯附加內力分布，如圖6所示.由圖可以看出，空洞的出現導致二襯產生的絕對值最大附加軸力和彎矩分別為-194.812 kN和-16.176 kN·m，出現在拱頂.

圖6 二襯附加內力分布Fig.6 Additional internal force distribution of the second lining

上述分析是深1.2 m空洞出現在拱頂，距離二襯1.2 m時得出的結論，很顯然，空洞的出現會改變二襯內力的分布，同時產生較大的附加軸力和彎矩，甚至改變彎矩的正負.拱頂區域同時出現正負彎矩，會使拱頂極易產生縱向裂縫，危及行車安全.

3 灰關聯分析

根據前文知道，對隧道進行無損檢測時在不同里程不同位置出現不同大小的空洞.因此以檢測數據和設計資料為依據通過隧道數值模型考慮隧道埋深、空洞深度、空洞距二襯距離和二襯厚度影響因素下二襯附加軸力和彎矩的變化規律，并引入灰色關聯理論，分別研究各影響因素與絕對值最大附加軸力和彎矩的關聯度.

3.1 灰色關聯理論

為了從隧道埋深、空洞深度、空洞距二襯距離、二襯厚度四個變量中分別選出影響二襯最大附加彎矩和軸力的主導因素，本文引入了灰色關聯理論進行分析.灰關聯分析優勢突出，通過對有限數據的分析，可以比較準確地量化比較因素與參考因素之間的關聯性(以關聯度表示)，關聯度越大，表明比較因素與參考因素的相關性越強[16].灰關聯分析步驟如下：

1) 確定比較列和參考列

本文以影響二襯最大附加彎矩和軸力的各因素(隧道埋深、空洞深度、空洞距二襯距離、二襯厚度)為比較列X，X=[X1,X2,…,Xm]T，分別以二襯最大附加彎矩和軸力作為參考列Y，Y=[Y1,Y2,…,Ym]T，其中，列X、Y的每個因素都有若干值，即Xi=[Xi(1),Xi(2),…,Xi(n)]，Yi=[Yi(1),Yi(2),…,Yi(n)]，因此列X、Y可寫成矩陣形式：

(1)

(2)

2) 矩陣的無量綱化

由于各影響因素的量綱不同，數量級較大，沒有可比性，因此必須對Xi和Yi進行無量綱處理.本文采用區間相對值化進行處理，計算方法如下：

(3)

3) 確定矩陣的灰關聯差異信息空間，差異矩陣如下:

(4)

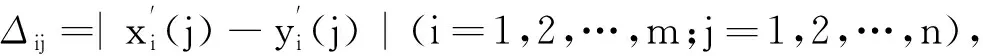
4) 求灰關聯系數矩陣與灰關聯度

關系系數可以由下式求出：

(5)

式中：ξ為分辨系數，ξ∈[0,1]，若越小，關聯系數間差異越大，區分能力越強，通常取ξ=0.5.由于關聯系數個數比較多，信息比較分散，對比分析較困難，因此通過計算平均值得到關聯度來進行影響因素關聯性的比較.關聯度由下式求得：

(6)

關聯度Ai[0,1]為區間內的變化量.關聯度序列中影響因素的關聯度相對越大，說明該影響因素對既有襯砌最大附加彎矩或附加軸力的影響越大，即其敏感性越大，反之則越不敏感.

3.2 各因素灰關聯分析

埋深分別為10 m、15 m、20 m、25 m、30 m時，空洞導致二襯最大附加內力的變化規律，如圖7(a)所示.從圖可以看出，附加彎矩和軸力的大小與埋深基本呈正相關，埋深從10 m增加到20 m,附加軸力的增長率較附加彎矩高，埋深達到20 m以后，二者基本趨于穩定.隨著隧道埋深的增加，襯砌受力趨于穩定，圍巖具有一定的自穩能力.

根據無損檢測的結果，空洞深度主要分布在0.3～1.5 m，因此在數值計算時空洞深度分別取0.3 m、0.6 m、0.9 m、1.2 m、1.5 m時，研究二襯附加內力的變化規律，如圖7(b)所示.從圖中可以明顯看出，二襯附加內力隨空洞深度的增大而逐漸增加，當空洞深度達到1.2 m以后，二襯附加內力急劇增加，附加最大彎矩的增加速率大于軸力.

根據現場無損檢測的結果，空洞距二襯距離主要分布在0～1.2 m之間，因此在數值計算中分別取空洞距二襯0 m、0.3 m、0.6 m、0.9 m、1.2 m時，研究二襯附加內力的變化規律，如圖7(c)所示.從圖可以看出，隨著距離的增加，二襯最大附加軸力逐漸減小，而最大附加彎矩逐漸增大，二者的差值先逐漸減小，趨于零以后，差值繼續增加并趨于穩定.

二襯厚度分別為30 cm、35 cm、40 cm、45 cm、50 cm時，二襯最大附加內力的變化規律，如圖7(d)所示.從圖可以看出，二襯最大附加軸力隨厚度的增大而緩慢減小，而二襯最大附加彎矩的減小速率較軸力大.當然厚度小的時候，截面積小結構受力小，容易產生裂縫.

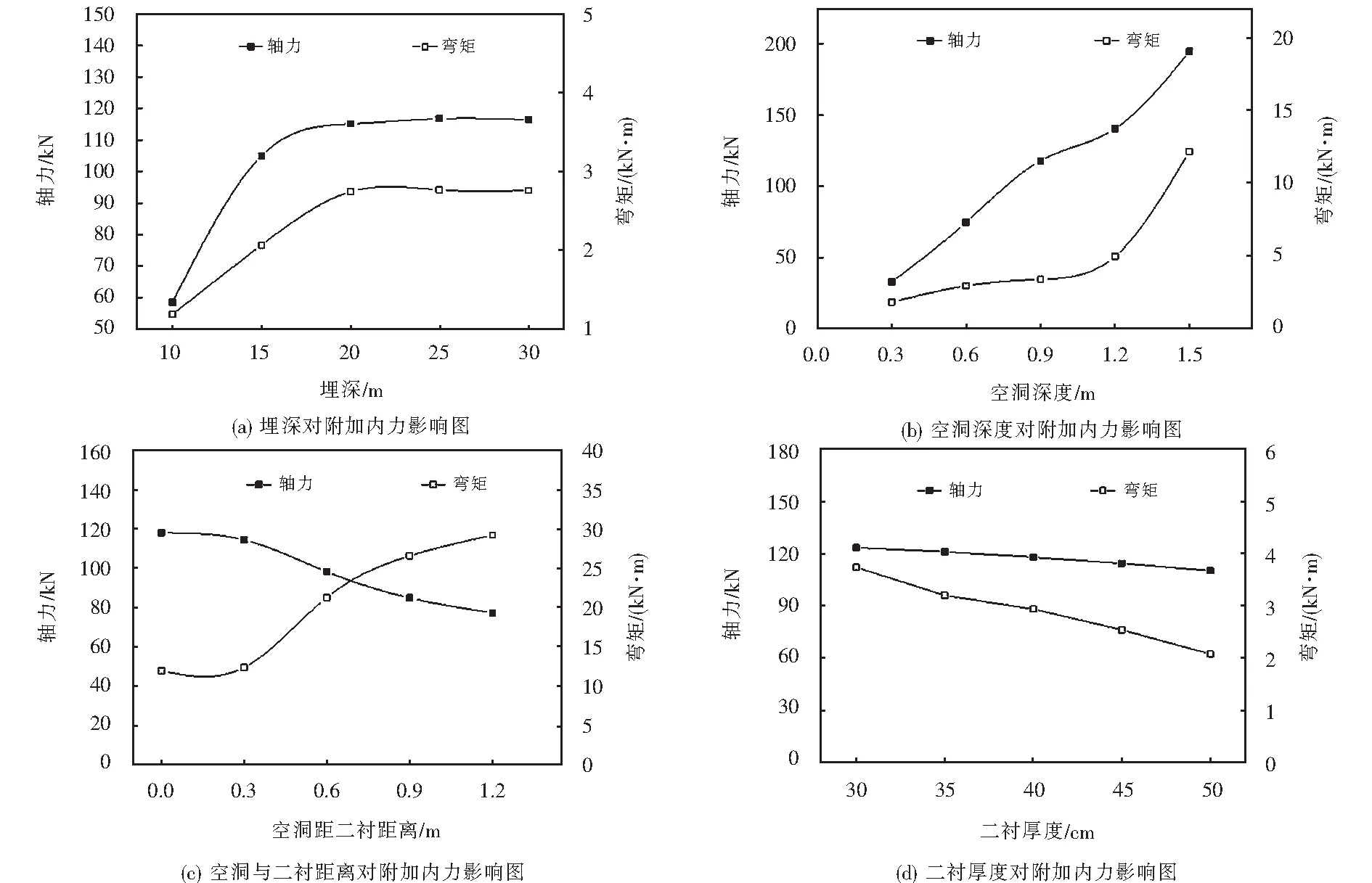
圖7 各影響因素下附加內力變化規律Fig.7 Change law of additional internal force under various influencing factors

將以上的數值分析結果利用上述灰色系統理論，可以分別計算各影響因子的附加內力影響程度.建立比較列，參考列如下：

(7)

其中：X1為隧道埋深；X2為空洞深度；X3為空洞距二襯距離；X4為二襯厚度.

(8)

其中：YF為X1，X2，X3，X4所對應的是絕對值最大附加軸力.

YM=

(9)

其中：YM為X1，X2，X3，X4所對應的是絕對值最大附加彎矩.

將以上(7)～(9)式代入式(3)～(6)計算灰色關聯度值，得到各影響因子的序列矩陣如下：

AF=[0.729 0.957 0.508 0.504].

AM=[0.768 0.779 0.491 0.537].

關聯度值表明，隧道埋深、空洞深度，空洞距二襯距離和二襯厚度對二襯附加內力的影響程度不同.二襯絕對值最大附加軸力影響程度主要取決于空洞深度，隧道埋深次之，空洞距二襯距離第三，二襯厚度次之.二襯絕對值最大附加彎矩影響程度主要取決于空洞深度，隧道埋深次之，二襯厚度第三，空洞距二襯距離次之.后續隧道病害整治應參考影響因素的敏感順序，為合理有效地提出病害整治方案提供參考.

4 結論

本文借助探地雷達對某既有隧道進行了無損檢測，建立相應的數值模型分析了空洞對襯砌受力的影響，同時引入灰色理論對各影響因素進行了灰關聯分析.通過分析，得出以下結論：

1) 通過對雷達圖像分析，空洞的剖面形狀呈橢圓狀，深度主要分布在0.3～1.5 m，長度約是深度的2倍，與襯砌的距離主要分布在0～1.2 m.

2) 空洞的出現改變了部分區域彎矩的正負.隨著埋深的增大，附加彎矩和軸力不斷增大，埋深達到20 m以后，二者基本趨于穩定，隨著空洞距二襯距離的增大，附加內力逐漸趨于穩定.

3) 隧道埋深、空洞深度、空洞距二襯距離和二襯厚度四種因素對二襯附加內力的影響程度不同，通過灰關聯分析，影響二襯附加內力的主要因素是空洞深度.根據各影響因素的敏感順序，為后續的病害綜合整治提供參考.